沪科版数学九年级上册23.1.2 锐角三角函数-正弦和余弦课件(共16张PPT)
文档属性
| 名称 | 沪科版数学九年级上册23.1.2 锐角三角函数-正弦和余弦课件(共16张PPT) |  | |
| 格式 | ppt | ||
| 文件大小 | 2.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-12-27 11:57:31 | ||
图片预览



文档简介
(共16张PPT)
“一个国家只有数学蓬勃发展,
才能表现它的国力强大”
——(法)拿破仑
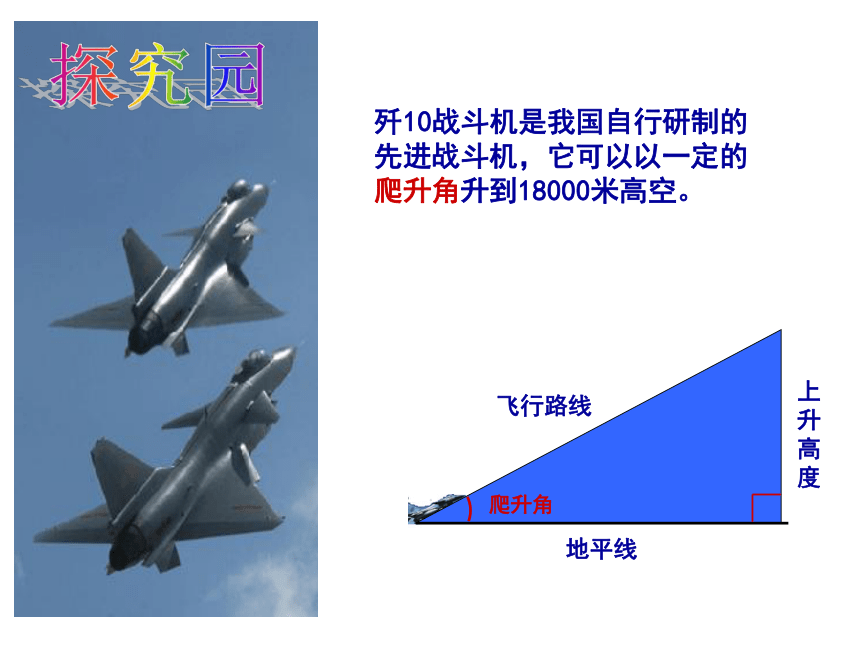
歼10战斗机是我国自行研制的先进战斗机,它可以以一定的爬升角升到18000米高空。
飞行路线
地平线
上
升
高
度
爬升角
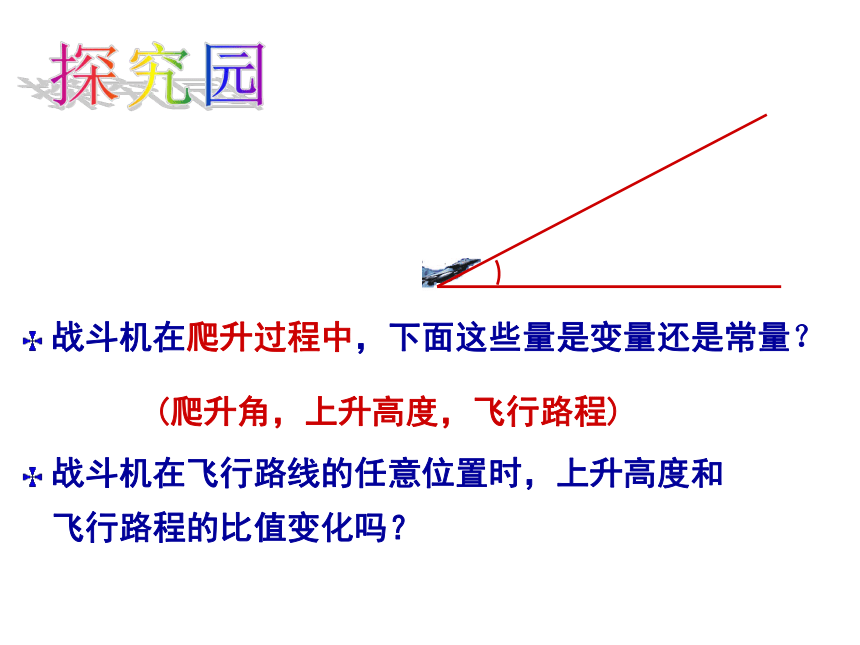
战斗机在爬升过程中,下面这些量是变量还是常量?
(爬升角,上升高度,飞行路程)
战斗机在飞行路线的任意位置时,上升高度和飞行路程的比值变化吗?
A
C
B
B1
C1
B
C
B1
C1
30°
45°
A
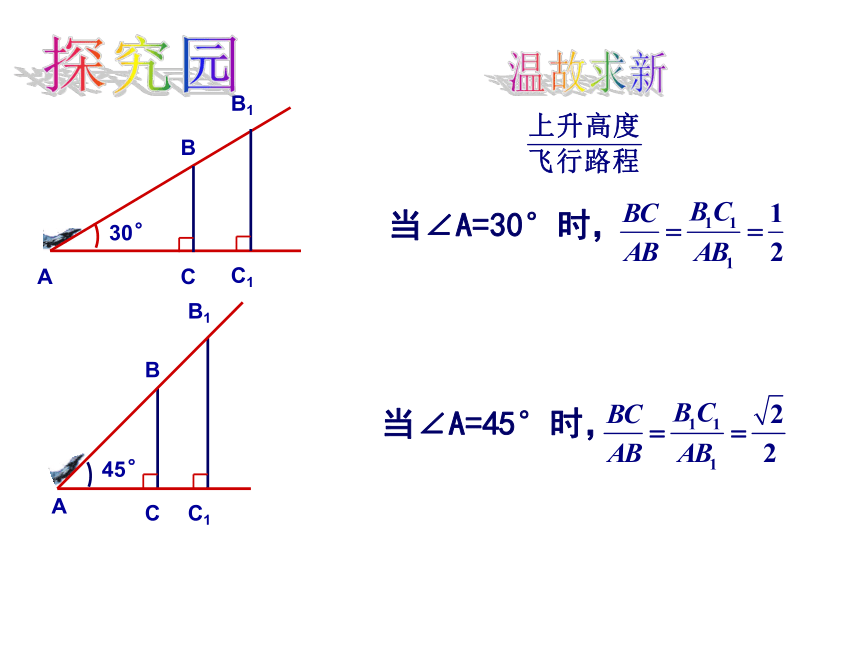
当∠A=30°时,
当∠A=45°时,
A
B
C
B1
C1
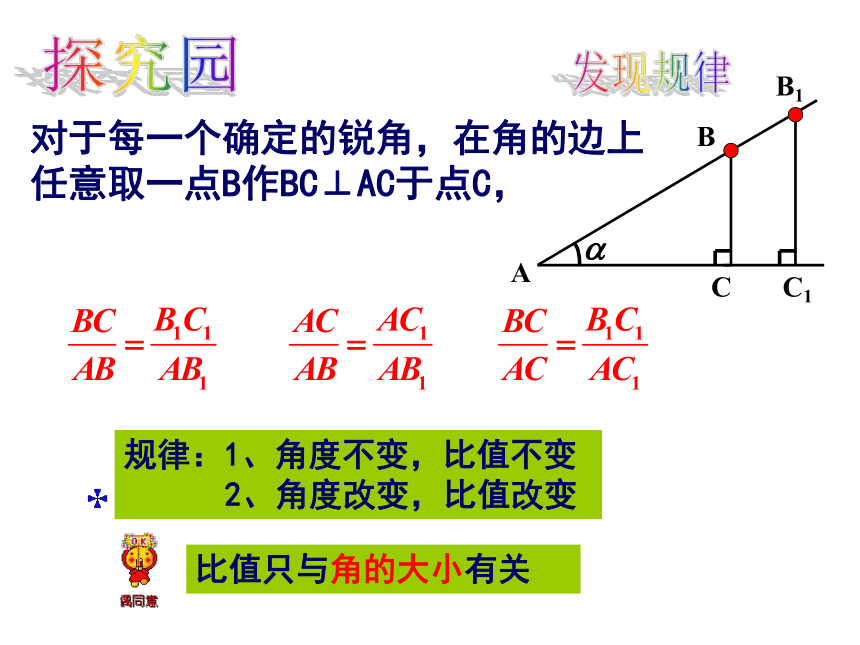
对于每一个确定的锐角,在角的边上
任意取一点B作BC⊥AC于点C,
规律:1、角度不变,比值不变
2、角度改变,比值改变
比值只与角的大小有关
比值 叫做∠ 的正弦(sine),记做sin 。
锐角 的正弦,余弦和正切统称∠ 的三角函数
比值 叫做∠ 的余弦(cosine) ,记做cos 。
比值 叫做∠ 的正切(tangent) ,记做tan 。
即tan =
即cos =
即sin =
A
B
C
B’
C’
正弦
余弦
正切
正对正
弦对斜
切无斜
0tanA﹥0
0sinA
cosA
tanA
=
=
=
一定要记住哦!
你能说出下面直角三角形中各锐角的三角函数吗?
B
B
C
A
G
F
E
A
C
②
①
③
b
a
c
是是非非(巩固类)
(1)、如图① sinA= ( )
(2)、如图① tanA= ( )
①
(3)、如图② cosA= ( )
C
A
B
4
5
②
注意1:定义要熟记
注意2:勾股定理要结合
注意3: Rt△是前提
×
√
×
B
C
A
┌
6
10
如图,在Rt△ABC中,∠ACB=90°,作CD⊥AB于D,
若BD=2,BC=3 ,求∠ A的正弦。
3
D
B
C
A
2
利用转化思想进行角的转化
(解答类)
如图,在等腰三角形ABC中,AB=AC=4,BC=6, 求∠B的余弦值和正切值。
C
A
B
D
┌
构造直角三角形计算三角函数值
4
3
(解答类)
cosB=
tanB=
解:作AD⊥BC于D,
∵AB=AC, AD⊥BC
∴BD= BC= ×6=3
在Rt△ABD中,BD=3,AB=4
∴AD=
∴在Rt△ABD中,
B
C
A
α
⑵如图,请你以射线AB为始边作锐角∠DAB,
使它的正切值为 ;
D
⑴在如图所示的格点图中,
请求出锐角 的三角函数值;
(拓展类)
一个概念三角函数
两种思想用来解题
三个注意必须牢记
sin =
cos =
tan =
三角函数
“一个国家只有数学蓬勃发展,
才能表现它的国力强大”
——(法)拿破仑
歼10战斗机是我国自行研制的先进战斗机,它可以以一定的爬升角升到18000米高空。
飞行路线
地平线
上
升
高
度
爬升角
战斗机在爬升过程中,下面这些量是变量还是常量?
(爬升角,上升高度,飞行路程)
战斗机在飞行路线的任意位置时,上升高度和飞行路程的比值变化吗?
A
C
B
B1
C1
B
C
B1
C1
30°
45°
A
当∠A=30°时,
当∠A=45°时,
A
B
C
B1
C1
对于每一个确定的锐角,在角的边上
任意取一点B作BC⊥AC于点C,
规律:1、角度不变,比值不变
2、角度改变,比值改变
比值只与角的大小有关
比值 叫做∠ 的正弦(sine),记做sin 。
锐角 的正弦,余弦和正切统称∠ 的三角函数
比值 叫做∠ 的余弦(cosine) ,记做cos 。
比值 叫做∠ 的正切(tangent) ,记做tan 。
即tan =
即cos =
即sin =
A
B
C
B’
C’
正弦
余弦
正切
正对正
弦对斜
切无斜
0
0
cosA
tanA
=
=
=
一定要记住哦!
你能说出下面直角三角形中各锐角的三角函数吗?
B
B
C
A
G
F
E
A
C
②
①
③
b
a
c
是是非非(巩固类)
(1)、如图① sinA= ( )
(2)、如图① tanA= ( )
①
(3)、如图② cosA= ( )
C
A
B
4
5
②
注意1:定义要熟记
注意2:勾股定理要结合
注意3: Rt△是前提
×
√
×
B
C
A
┌
6
10
如图,在Rt△ABC中,∠ACB=90°,作CD⊥AB于D,
若BD=2,BC=3 ,求∠ A的正弦。
3
D
B
C
A
2
利用转化思想进行角的转化
(解答类)
如图,在等腰三角形ABC中,AB=AC=4,BC=6, 求∠B的余弦值和正切值。
C
A
B
D
┌
构造直角三角形计算三角函数值
4
3
(解答类)
cosB=
tanB=
解:作AD⊥BC于D,
∵AB=AC, AD⊥BC
∴BD= BC= ×6=3
在Rt△ABD中,BD=3,AB=4
∴AD=
∴在Rt△ABD中,
B
C
A
α
⑵如图,请你以射线AB为始边作锐角∠DAB,
使它的正切值为 ;
D
⑴在如图所示的格点图中,
请求出锐角 的三角函数值;
(拓展类)
一个概念三角函数
两种思想用来解题
三个注意必须牢记
sin =
cos =
tan =
三角函数
