沪科版数学九年级上册22.1黄金分割课件(共14张PPT)
文档属性
| 名称 | 沪科版数学九年级上册22.1黄金分割课件(共14张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 2.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-12-27 12:24:52 | ||
图片预览




文档简介
(共14张PPT)
黄金分割
Huang Jin Fen Ge
美图欣赏
让我们从数学的角度来研究
位于上海黄浦江畔的东方明珠塔,是亚洲第一,世界第三高塔,它的塔身竟高达468米。要建造这样高而瘦长搭塔身,在造型上难免有些单调,然而设计师巧妙地在塔身上装置了晶莹耀眼的上球体、下球体和太空舱,它既可供游人登高俯览城市景色,又使笔直的塔身有了曲线变化,更妙的是,设计师有意将上球体选在263至308米之间的位置,使塔身显得非常协调、美观。举世闻名的法国巴黎埃菲尔铁塔,都是根据黄金分割的原理来建造的。
A
B
C
AB= 468米
AC=178.7米
≈
≈
0.618
0.618
≈
BC=289.3米
探究发现
如图,点 C 把线段 AB 分成两条线段 AC 和 BC ,
那么称线段 AB 被点 C 黄金分割(golden section),点 C 叫做线段 AB 的黄金分割点,
如果
(
)
●
D
AC
AB
AC
BC
=
C
A
B
AC 与 AB 的比叫做黄金数.
如何求得这个比值呢?
一条线段有两个黄金分割点
新知归纳
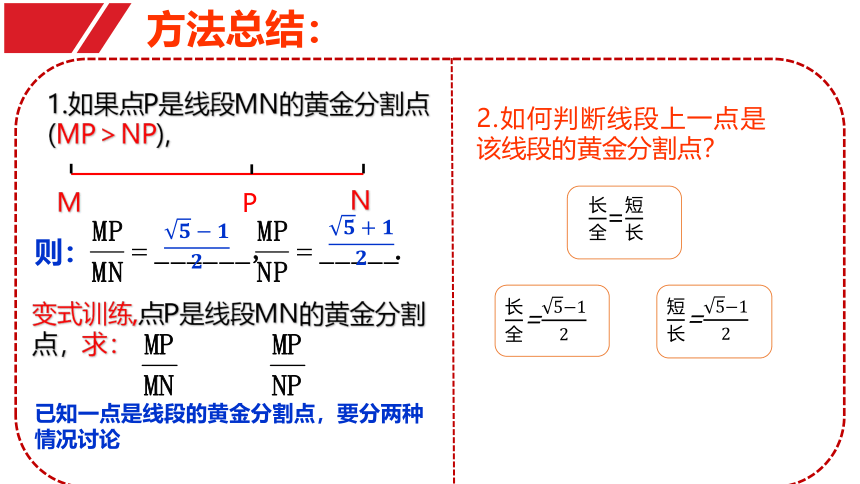
方法总结:
2.如何判断线段上一点是该线段的黄金分割点?
已知一点是线段的黄金分割点,要分两种情况讨论
=
=
=
1.如果点P是线段MN的黄金分割点(MP>NP),
N
M
P
则:
变式训练,点P是线段MN的黄金分割点,求:
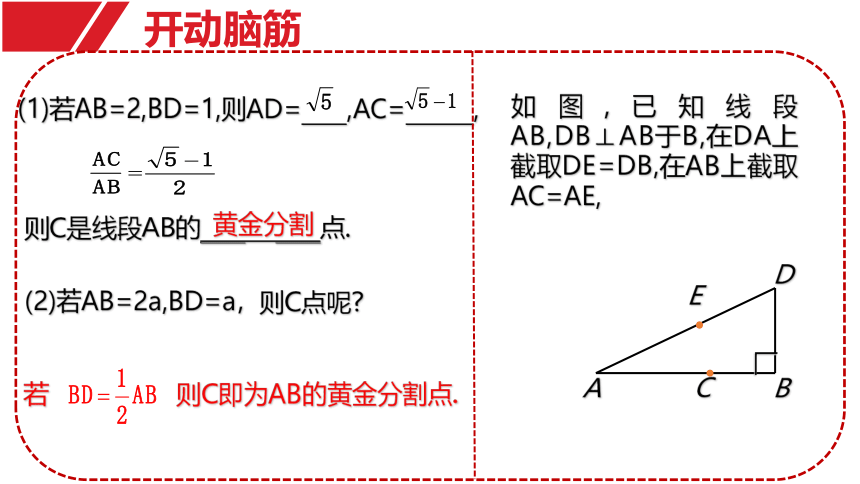
开动脑筋
如图,已知线段AB,DB⊥AB于B,在DA上截取DE=DB,在AB上截取AC=AE,
(1)若AB=2,BD=1,则AD=____,AC=______,
则C是线段AB的____ ____点.
黄金分割
(2)若AB=2a,BD=a,
则C点呢
E
A
B
D
C
∟
若
则C即为AB的黄金分割点.
1、经过点B作BD⊥AB,
2、连接AD,
3、在AB上截取 AC=AE.
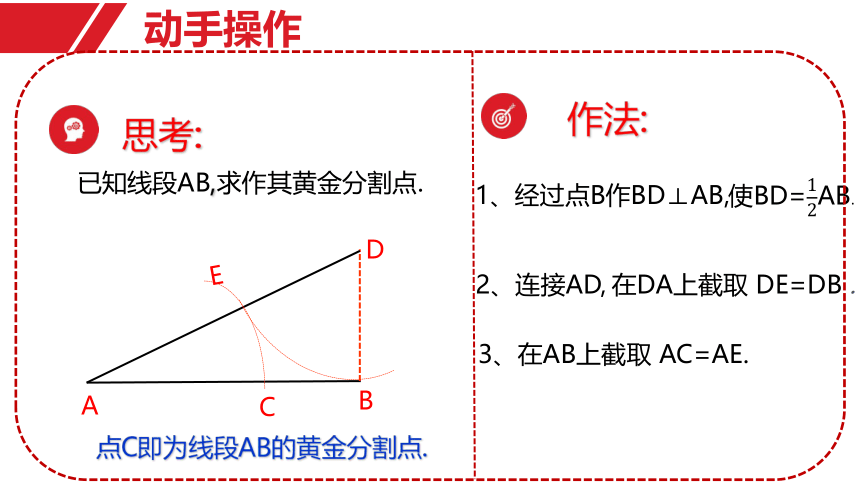
作法:
已知线段AB,求作其黄金分割点.
点C即为线段AB的黄金分割点.
A
B
D
E
C
思考:
使BD=AB.
在DA上截取 DE=DB .
动手操作
D
深入探究
A
B
C
C
E
F
神奇的黄金矩形
G
H
如图,B是线段AC的黄金分割点(AB>BC),
以AB,BC的长为边长作矩形,
这样的矩形称为黄金矩形。
则该矩形的短边与长边的比值是黄金数
思考:如上图,在黄金矩形ABCD切掉正方形BCFE,剩下的矩形AEFD还是黄金矩形吗?
E是AB的黄金分割点吗?
这幅《蒙娜丽莎的微笑》给了数以亿万计的人们美的艺术享受,备受推崇。意大利画家达芬奇在创作中大量运用了黄金矩形来构图。整个画面使人觉得和谐自然,优雅安宁。
找一找:画中有几个黄金矩形?
黄金矩形的“迷人面容”----蒙娜丽莎的微笑。
回归生活
芭蕾舞演员踮起脚尖起舞时,动作显得更加优美,身体也显得更加修长,此时从头顶到肚脐与从肚脐到足尖部分的比值接近黄金比值。
足尖上的艺术——芭蕾
回归生活
摄影构图中的黄金分割
在很多优秀的摄影作品中,运用黄金分割法进行构图,可以有效地控制主体的位置及主体和环境的关系,从而使画面更加自然、和谐、生动。
回归生活
新知巩固
2、
3
4、
我学会-------------------------
我知道了-------------------------
我还有疑惑是----------------------
课堂回顾:
分层作业:
1、课后查阅资料,生活中还有哪些美的事物与黄金分割有关?并且能够结合本节课所学内容加以理解。
2、若点C是线段AB的黄金分割点,求和
拓展延伸
科学研究表明,当人的下肢长与身高之比为0.618时,看起来最美.某成年女士身高为153cm,下肢长为92cm,她的高跟鞋鞋跟最佳高度约为______cm(结果精确到0.1cm).
黄金分割
Huang Jin Fen Ge
美图欣赏
让我们从数学的角度来研究
位于上海黄浦江畔的东方明珠塔,是亚洲第一,世界第三高塔,它的塔身竟高达468米。要建造这样高而瘦长搭塔身,在造型上难免有些单调,然而设计师巧妙地在塔身上装置了晶莹耀眼的上球体、下球体和太空舱,它既可供游人登高俯览城市景色,又使笔直的塔身有了曲线变化,更妙的是,设计师有意将上球体选在263至308米之间的位置,使塔身显得非常协调、美观。举世闻名的法国巴黎埃菲尔铁塔,都是根据黄金分割的原理来建造的。
A
B
C
AB= 468米
AC=178.7米
≈
≈
0.618
0.618
≈
BC=289.3米
探究发现
如图,点 C 把线段 AB 分成两条线段 AC 和 BC ,
那么称线段 AB 被点 C 黄金分割(golden section),点 C 叫做线段 AB 的黄金分割点,
如果
(
)
●
D
AC
AB
AC
BC
=
C
A
B
AC 与 AB 的比叫做黄金数.
如何求得这个比值呢?
一条线段有两个黄金分割点
新知归纳
方法总结:
2.如何判断线段上一点是该线段的黄金分割点?
已知一点是线段的黄金分割点,要分两种情况讨论
=
=
=
1.如果点P是线段MN的黄金分割点(MP>NP),
N
M
P
则:
变式训练,点P是线段MN的黄金分割点,求:
开动脑筋
如图,已知线段AB,DB⊥AB于B,在DA上截取DE=DB,在AB上截取AC=AE,
(1)若AB=2,BD=1,则AD=____,AC=______,
则C是线段AB的____ ____点.
黄金分割
(2)若AB=2a,BD=a,
则C点呢
E
A
B
D
C
∟
若
则C即为AB的黄金分割点.
1、经过点B作BD⊥AB,
2、连接AD,
3、在AB上截取 AC=AE.
作法:
已知线段AB,求作其黄金分割点.
点C即为线段AB的黄金分割点.
A
B
D
E
C
思考:
使BD=AB.
在DA上截取 DE=DB .
动手操作
D
深入探究
A
B
C
C
E
F
神奇的黄金矩形
G
H
如图,B是线段AC的黄金分割点(AB>BC),
以AB,BC的长为边长作矩形,
这样的矩形称为黄金矩形。
则该矩形的短边与长边的比值是黄金数
思考:如上图,在黄金矩形ABCD切掉正方形BCFE,剩下的矩形AEFD还是黄金矩形吗?
E是AB的黄金分割点吗?
这幅《蒙娜丽莎的微笑》给了数以亿万计的人们美的艺术享受,备受推崇。意大利画家达芬奇在创作中大量运用了黄金矩形来构图。整个画面使人觉得和谐自然,优雅安宁。
找一找:画中有几个黄金矩形?
黄金矩形的“迷人面容”----蒙娜丽莎的微笑。
回归生活
芭蕾舞演员踮起脚尖起舞时,动作显得更加优美,身体也显得更加修长,此时从头顶到肚脐与从肚脐到足尖部分的比值接近黄金比值。
足尖上的艺术——芭蕾
回归生活
摄影构图中的黄金分割
在很多优秀的摄影作品中,运用黄金分割法进行构图,可以有效地控制主体的位置及主体和环境的关系,从而使画面更加自然、和谐、生动。
回归生活
新知巩固
2、
3
4、
我学会-------------------------
我知道了-------------------------
我还有疑惑是----------------------
课堂回顾:
分层作业:
1、课后查阅资料,生活中还有哪些美的事物与黄金分割有关?并且能够结合本节课所学内容加以理解。
2、若点C是线段AB的黄金分割点,求和
拓展延伸
科学研究表明,当人的下肢长与身高之比为0.618时,看起来最美.某成年女士身高为153cm,下肢长为92cm,她的高跟鞋鞋跟最佳高度约为______cm(结果精确到0.1cm).
