4.6用相似三角形测量高度 课件(共27张PPT)
文档属性
| 名称 | 4.6用相似三角形测量高度 课件(共27张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 1.4MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-12-28 08:38:43 | ||
图片预览







文档简介
(共27张PPT)
4.6 用相似三角形测量高度
第四章
图形的相似
2021-2022学年九年级数学上册同步(北师版)
学习目标
1.学生通过探索实际问题来体验测量中对相似三角形有关知识的应用。
2.经历应用相似三角形的有关知识去解决简单的实际问题的全过程。
3.全力培养学生的应用意识,和把实际问题转化为数学问题并用数学方法去分析、解决实际问题的能力。
导入新课
问题:相似三角形的判定方法有哪些?
① 两角对应相等,两三角形相似.
② 两边对应成比例且夹角相等,两三角形相似.
③ 三边对应成比例,两三角形相似.
B’
A’
C’
B
A
C
导入新课
在古希腊,有一位伟大的科学家叫泰勒斯.泰勒斯年轻时是一名商人,到过不少东方国家.一年春天,泰勒斯来到埃及,埃及法老对他说:“听说你什么都知道,那就请你测量一下埃及金字塔的高度吧!”这在当时的条件下是个大难题,因为是很难爬到塔顶的.你知道泰勒斯是怎样测量大金字塔的高度的吗?
利用相似三角形的原理,在金字塔影子的顶部立一根木杆,借助太阳光线构成两个相似三角形,来测量金字塔的高度.
运用相似三角形解决高度(长度)测量问题
一、利用阳光下的影子测量旗杆高度
利用阳光下的影子:
如图,每个小组选一名同学直立于旗杆影子的顶端处,其他人分为两部分,一部分同学测量该同学的影长,另一部分同学测量同一
时刻旗杆的影长.根据测量数
据,你能求出旗杆的高度吗?
说明你的理由.
C
A
E
B
D
探究新知
方法:表达式:物1高 :物2高 = 影1长 :影2长
测高方法一:
测量原理:测量不能到达顶部的物体的高度,可以用“在同一时刻物高与影长成正比例”的原理解决.
数据:需要测量人的高度,影长和旗杆的影长
优点:只需要皮尺就行;不受阳光的限制
缺点:计算量比较大
探究新知
二、利用标杆测量旗杆高度
如图,每个小组选一名同学作为观察者,在观察者与旗杆质检的地面上直立一根高度适当的标杆。观察者适当调整自己所处的位置,使旗杆的顶端、标杆的顶端与自己的眼镜恰好在一条直线上,这时其他同学立即测出观察者的脚到旗杆地段的距离,已经观察者的脚到标杆地段的距离,然后测出标杆的高。
根据测量数据,你能求出旗杆的高度吗?说明你的理由。
探究新知
探究新知
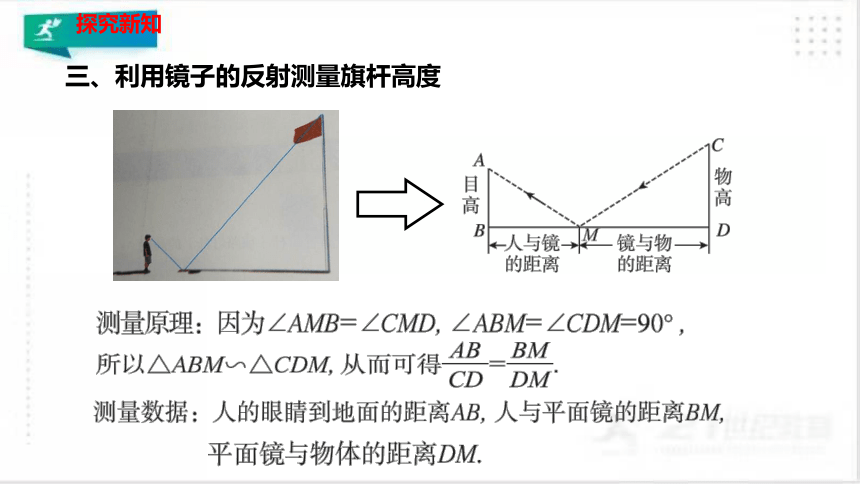
三、利用镜子的反射测量旗杆高度
探究新知
[明确] 平面镜反射原理:入射角等于反射角.
探究新知
例1.如图,在距离AB 18米的地面上平放着一面镜子E,人退后到距镜子2.1米的D处,在镜子里恰看见树顶,若人眼距地面1.4米,求树高。
18米
1.4米
2.1米
B
D
A
E
C
∵△ABE∽△CDE
∴ =
CD D E
AB BE
分析:设树高x米
x
x=12
即树高为12米
∴ =
x 18
1.4 2.1
例题讲解
例2 如图,小明为了测量一棵树CD的高度,他在距树24m处立了一根高为2m的标杆EF,然后小明前后调整自己的位置,当他与树相距27m的时候,他的眼睛、标杆的顶端和树的顶端在同一条直线上.已知小明的眼高1.6m,求树的高度.
A
E
C
D
F
B
N
例题讲解
A
E
C
D
F
B
N
解:过点A作AN//BD交CD于N,交EF于M,因为人、标杆、树都垂直于地面,
∴∠ABF=∠EFD=∠CDF=90°
∴AB//EF//CD, ∴∠EMA=∠CNA
∵∠EAM=∠CAN
∴△AEM∽△ACN
∴
∵AB=1.6m , EF=2m , BD=27m , FD=24m
∴ , ∴CN=3.6(m)
∴CD=3.6+1.6=5.2(m)
故树的高度为5.2m
例题讲解
例3 为了测量一棵大树的高度,某同学利用手边的工具(镜子、皮尺)设计了如下测量方案:如图,
①在距离树AB底部15m的E处放下镜子;
②该同学站在距离镜子1.2m的C处,目高CD为1.5m;
③观察镜面,恰好看到树的顶端.
你能帮助他计算出大树的大约高度吗?
解:∵∠1=∠2,∠DCE=∠BAE=90°
∴△DCE∽△BAE.
∴
解得 BA=18.75(m)
因此,树高约为18.75m.
D
A
C
E
2
1
B
例题讲解
(1)根据题意画出___________;
(2)将题目中的已知量或已知关系转化为示意图中的
_____________________;
(3)利用相似三角形建立线段之间的关系,求出
__________;
(4)写出___________.
示意图
已知线段、已知角
未知量
答案
利用三角形相似解决实际问题的一般步骤:
例题讲解
1.要测量出一棵树的高度,除了测量出人高与人的影长外,还需要测出( )
A.仰角 B.树的影长
C.标杆的影长 D.都不需要
B
课堂练习
2.如图,是小玲设计用手电来测量某古城墙高度的示意图.在点P处放一水平的平面镜,光线从点A出发经平面镜反射后,刚好射到古城墙CD的顶端C处.已知AB⊥BD,CD⊥BD.且测得AB=1.2m,BP=1.8m,PD=12m.那么该古城墙CD的高度是( )
A.6m B.8m C.18m D.21m
B
课堂练习
3.某校数学兴趣小组为测量学校旗杆AC的高度,在点F处竖立一根长为1.5m的标杆DF,如右图,量出DF的影子EF的长度为1m,同一时刻测量旗杆AC的影子BC的长度为6m,那么旗杆AC的高度为( )
A.6m B.7m
C.8.5m D.9m
D
课堂练习
4.如右图,小明用长为3m的竹竿CD做测量工具,测量学校旗杆AB的高度,移动竹竿,使竹竿与旗杆的距离DB=12m,则旗杆AB的高为_____.
9m
课堂练习
5.铁道口的栏杆短臂长1m,长臂长16m,当短臂端点下降0.5m时,长臂端点升高______m.
8
O
B
D
C
A
┏
┛
1m
16m
0.5m
?
课堂练习
6.如图所示,王刚同学所在的学习小组欲测量校园里一棵大树的高度,他们选王刚作为观测者,并在王刚与大树之间的地面上直立一根高为2 m的标杆CD,然后,王刚开始调整自己的位置,当他看到标杆的顶端C与树的顶端E重合时,就在该位置停止不动,这时其他同学通过测量,发现王刚离标杆的距离为1 m,
离大树底部的距离为9 m,王刚的眼睛离地
面的高度AB为1.5 m,那么大树EF的高度
为多少?
课堂练习
解:如图所示,过点A作AH⊥EF,垂足为H,交CD于点G.
G
H
课堂练习
7.如图,为了估算河的宽度,我们可以在河的对岸选定一个目标作为点A,再在河的这一边选定点B和点C,使AB⊥BC,然后,再选点E,使EC⊥BC,用视线确定BC和AE的交点D,此时如果测得BD=118米,DC=61米,EC=50米,求河的宽度AB.(精确到0.1米)
A
D
C
E
B
课堂练习
解:∵∠ADB=∠EDC
∠ABD=∠ECD=90゜
答:河的宽度AB约为96.7米.
∴⊿ABD∽⊿ECD
(两角分别相等的两个三角形相似),
∴
解得
A
D
C
E
B
课堂练习
课堂小结
相似三角形的应用
测量高度问题
测量河宽问题
https://www.21cnjy.com/help/help_extract.php
4.6 用相似三角形测量高度
第四章
图形的相似
2021-2022学年九年级数学上册同步(北师版)
学习目标
1.学生通过探索实际问题来体验测量中对相似三角形有关知识的应用。
2.经历应用相似三角形的有关知识去解决简单的实际问题的全过程。
3.全力培养学生的应用意识,和把实际问题转化为数学问题并用数学方法去分析、解决实际问题的能力。
导入新课
问题:相似三角形的判定方法有哪些?
① 两角对应相等,两三角形相似.
② 两边对应成比例且夹角相等,两三角形相似.
③ 三边对应成比例,两三角形相似.
B’
A’
C’
B
A
C
导入新课
在古希腊,有一位伟大的科学家叫泰勒斯.泰勒斯年轻时是一名商人,到过不少东方国家.一年春天,泰勒斯来到埃及,埃及法老对他说:“听说你什么都知道,那就请你测量一下埃及金字塔的高度吧!”这在当时的条件下是个大难题,因为是很难爬到塔顶的.你知道泰勒斯是怎样测量大金字塔的高度的吗?
利用相似三角形的原理,在金字塔影子的顶部立一根木杆,借助太阳光线构成两个相似三角形,来测量金字塔的高度.
运用相似三角形解决高度(长度)测量问题
一、利用阳光下的影子测量旗杆高度
利用阳光下的影子:
如图,每个小组选一名同学直立于旗杆影子的顶端处,其他人分为两部分,一部分同学测量该同学的影长,另一部分同学测量同一
时刻旗杆的影长.根据测量数
据,你能求出旗杆的高度吗?
说明你的理由.
C
A
E
B
D
探究新知
方法:表达式:物1高 :物2高 = 影1长 :影2长
测高方法一:
测量原理:测量不能到达顶部的物体的高度,可以用“在同一时刻物高与影长成正比例”的原理解决.
数据:需要测量人的高度,影长和旗杆的影长
优点:只需要皮尺就行;不受阳光的限制
缺点:计算量比较大
探究新知
二、利用标杆测量旗杆高度
如图,每个小组选一名同学作为观察者,在观察者与旗杆质检的地面上直立一根高度适当的标杆。观察者适当调整自己所处的位置,使旗杆的顶端、标杆的顶端与自己的眼镜恰好在一条直线上,这时其他同学立即测出观察者的脚到旗杆地段的距离,已经观察者的脚到标杆地段的距离,然后测出标杆的高。
根据测量数据,你能求出旗杆的高度吗?说明你的理由。
探究新知
探究新知
三、利用镜子的反射测量旗杆高度
探究新知
[明确] 平面镜反射原理:入射角等于反射角.
探究新知
例1.如图,在距离AB 18米的地面上平放着一面镜子E,人退后到距镜子2.1米的D处,在镜子里恰看见树顶,若人眼距地面1.4米,求树高。
18米
1.4米
2.1米
B
D
A
E
C
∵△ABE∽△CDE
∴ =
CD D E
AB BE
分析:设树高x米
x
x=12
即树高为12米
∴ =
x 18
1.4 2.1
例题讲解
例2 如图,小明为了测量一棵树CD的高度,他在距树24m处立了一根高为2m的标杆EF,然后小明前后调整自己的位置,当他与树相距27m的时候,他的眼睛、标杆的顶端和树的顶端在同一条直线上.已知小明的眼高1.6m,求树的高度.
A
E
C
D
F
B
N
例题讲解
A
E
C
D
F
B
N
解:过点A作AN//BD交CD于N,交EF于M,因为人、标杆、树都垂直于地面,
∴∠ABF=∠EFD=∠CDF=90°
∴AB//EF//CD, ∴∠EMA=∠CNA
∵∠EAM=∠CAN
∴△AEM∽△ACN
∴
∵AB=1.6m , EF=2m , BD=27m , FD=24m
∴ , ∴CN=3.6(m)
∴CD=3.6+1.6=5.2(m)
故树的高度为5.2m
例题讲解
例3 为了测量一棵大树的高度,某同学利用手边的工具(镜子、皮尺)设计了如下测量方案:如图,
①在距离树AB底部15m的E处放下镜子;
②该同学站在距离镜子1.2m的C处,目高CD为1.5m;
③观察镜面,恰好看到树的顶端.
你能帮助他计算出大树的大约高度吗?
解:∵∠1=∠2,∠DCE=∠BAE=90°
∴△DCE∽△BAE.
∴
解得 BA=18.75(m)
因此,树高约为18.75m.
D
A
C
E
2
1
B
例题讲解
(1)根据题意画出___________;
(2)将题目中的已知量或已知关系转化为示意图中的
_____________________;
(3)利用相似三角形建立线段之间的关系,求出
__________;
(4)写出___________.
示意图
已知线段、已知角
未知量
答案
利用三角形相似解决实际问题的一般步骤:
例题讲解
1.要测量出一棵树的高度,除了测量出人高与人的影长外,还需要测出( )
A.仰角 B.树的影长
C.标杆的影长 D.都不需要
B
课堂练习
2.如图,是小玲设计用手电来测量某古城墙高度的示意图.在点P处放一水平的平面镜,光线从点A出发经平面镜反射后,刚好射到古城墙CD的顶端C处.已知AB⊥BD,CD⊥BD.且测得AB=1.2m,BP=1.8m,PD=12m.那么该古城墙CD的高度是( )
A.6m B.8m C.18m D.21m
B
课堂练习
3.某校数学兴趣小组为测量学校旗杆AC的高度,在点F处竖立一根长为1.5m的标杆DF,如右图,量出DF的影子EF的长度为1m,同一时刻测量旗杆AC的影子BC的长度为6m,那么旗杆AC的高度为( )
A.6m B.7m
C.8.5m D.9m
D
课堂练习
4.如右图,小明用长为3m的竹竿CD做测量工具,测量学校旗杆AB的高度,移动竹竿,使竹竿与旗杆的距离DB=12m,则旗杆AB的高为_____.
9m
课堂练习
5.铁道口的栏杆短臂长1m,长臂长16m,当短臂端点下降0.5m时,长臂端点升高______m.
8
O
B
D
C
A
┏
┛
1m
16m
0.5m
?
课堂练习
6.如图所示,王刚同学所在的学习小组欲测量校园里一棵大树的高度,他们选王刚作为观测者,并在王刚与大树之间的地面上直立一根高为2 m的标杆CD,然后,王刚开始调整自己的位置,当他看到标杆的顶端C与树的顶端E重合时,就在该位置停止不动,这时其他同学通过测量,发现王刚离标杆的距离为1 m,
离大树底部的距离为9 m,王刚的眼睛离地
面的高度AB为1.5 m,那么大树EF的高度
为多少?
课堂练习
解:如图所示,过点A作AH⊥EF,垂足为H,交CD于点G.
G
H
课堂练习
7.如图,为了估算河的宽度,我们可以在河的对岸选定一个目标作为点A,再在河的这一边选定点B和点C,使AB⊥BC,然后,再选点E,使EC⊥BC,用视线确定BC和AE的交点D,此时如果测得BD=118米,DC=61米,EC=50米,求河的宽度AB.(精确到0.1米)
A
D
C
E
B
课堂练习
解:∵∠ADB=∠EDC
∠ABD=∠ECD=90゜
答:河的宽度AB约为96.7米.
∴⊿ABD∽⊿ECD
(两角分别相等的两个三角形相似),
∴
解得
A
D
C
E
B
课堂练习
课堂小结
相似三角形的应用
测量高度问题
测量河宽问题
https://www.21cnjy.com/help/help_extract.php
同课章节目录
- 第一章 特殊平行四边形
- 1 菱形的性质与判定
- 2 矩形的性质与判定
- 3 正方形的性质与判定
- 第二章 一元二次方程
- 1 认识一元二次方程
- 2 用配方法求解一元二次方程
- 3 用公式法求解一元二次方程
- 4 用因式分解法求解一元二次方程
- 5 一元二次方程的根与系数的关系
- 6 应用一元二次方程
- 第三章 概率的进一步认识
- 1 用树状图或表格求概率
- 2 用频率估计概率
- 第四章 图形的相似
- 1 成比例线段
- 2 平行线分线段成比例
- 3 相似多边形
- 4 探索三角形相似的条件
- 5 相似三角形判定定理的证明
- 6 利用相似三角形测高
- 7 相似三角形的性质
- 8 图形的位似
- 第五章 投影与视图
- 1 投影
- 2 视图
- 第六章 反比例函数
- 1 反比例函数
- 2 反比例函数的图象与性质
- 3 反比例函数的应用
