沪科版数学九年级上册 第23章解直角三角形复习 课件(共22张PPT)
文档属性
| 名称 | 沪科版数学九年级上册 第23章解直角三角形复习 课件(共22张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 502.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-12-27 12:58:28 | ||
图片预览




文档简介
(共22张PPT)
解直角三角形
解直角三角形复习
生活问题
一
知识梳理
二
试题归类
三
思维训练
四
讨论交流
五
下页
上页
首页
末页
中考练兵
六
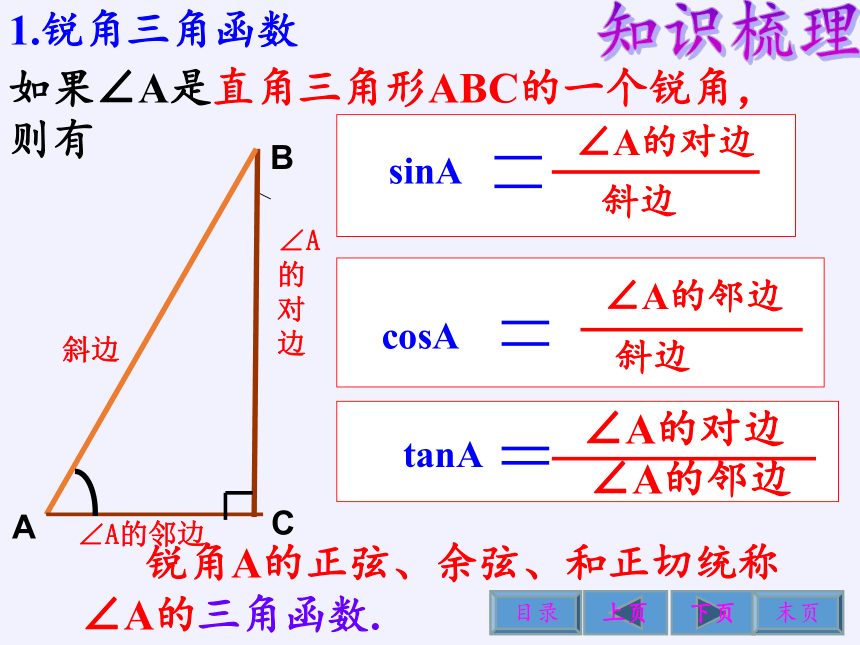
如果∠A是直角三角形ABC的一个锐角, 则有
∠A的对边
∠A的邻边
tanA
cosA
∠A的邻边
∠A的对边
斜边
sinA
斜边
B
C
A
∠A的对边
∠A的邻边
斜边
锐角A的正弦、余弦、和正切统称∠A的三角函数.
1.锐角三角函数
知识梳理
下页
上页
目录
末页
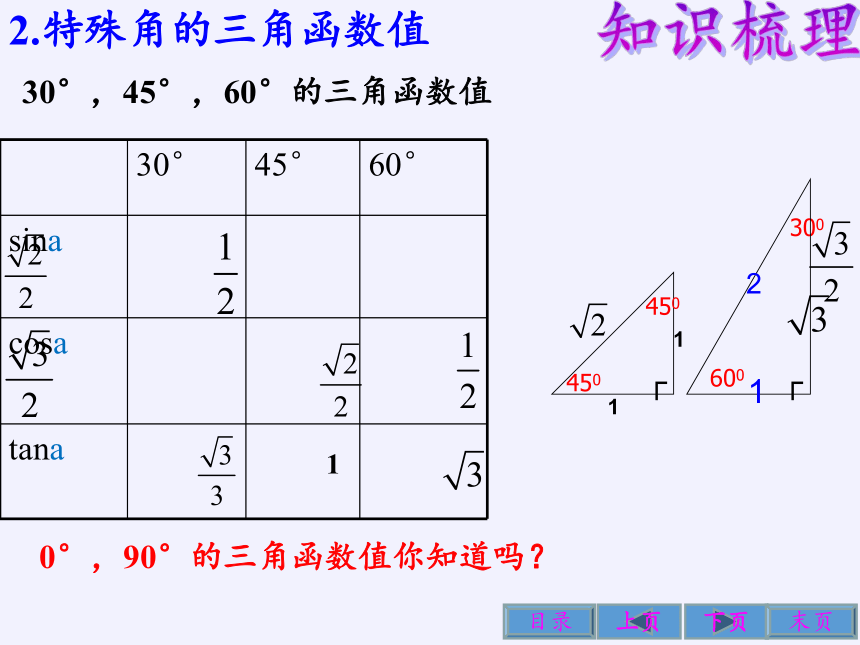
30°,45°,60°的三角函数值
30° 45° 60°
sina
cosa
tana
1
300
┌
┌
450
450
600
1
2
1
1
2.特殊角的三角函数值
0°,90°的三角函数值你知道吗?
知识梳理
下页
上页
目录
末页
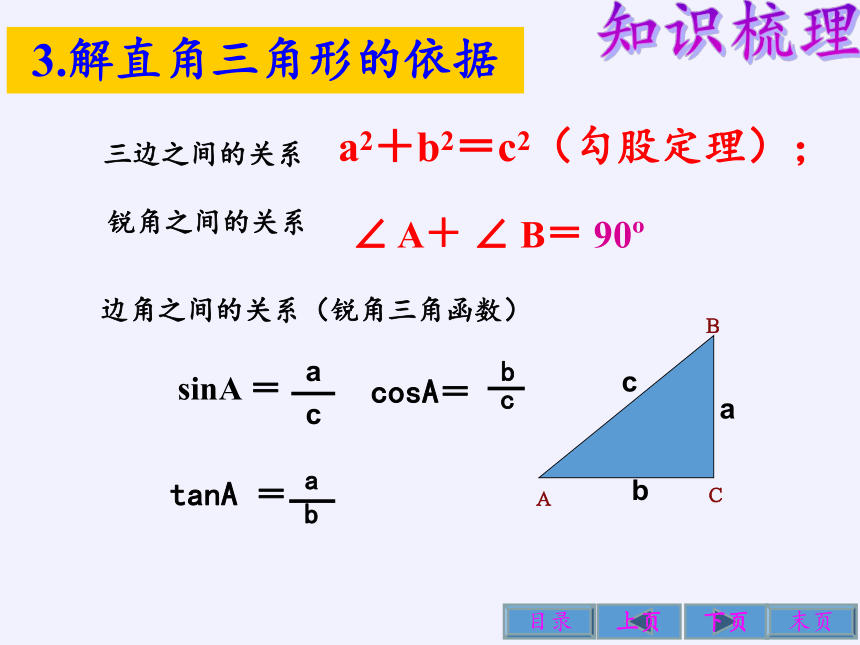
三边之间的关系
a2+b2=c2(勾股定理);
锐角之间的关系
∠ A+ ∠ B= 90
边角之间的关系(锐角三角函数)
tanA =
a
b
sinA =
a
c
cosA=
b
c
A
C
B
a
b
c
3.解直角三角形的依据
知识梳理
下页
上页
目录
末页
(09·滨州)某楼梯侧面视图如图,其中AB=4m,∠BAC=30°,∠C=90°,因某种活动,要求铺设红色地毯,则在AB段楼梯所铺地毯的长应 。
B
C
A
生活问题
下页
上页
目录
末页
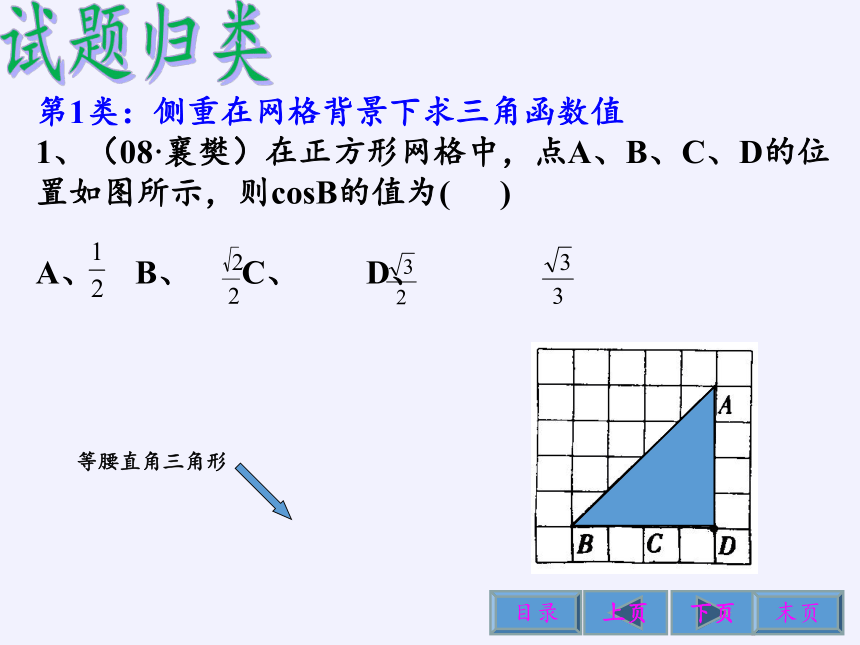
第1类:侧重在网格背景下求三角函数值
1、(08·襄樊)在正方形网格中,点A、B、C、D的位置如图所示,则cosB的值为( )
A、 B、 C、 D、
等腰直角三角形
试题归类
下页
上页
目录
末页
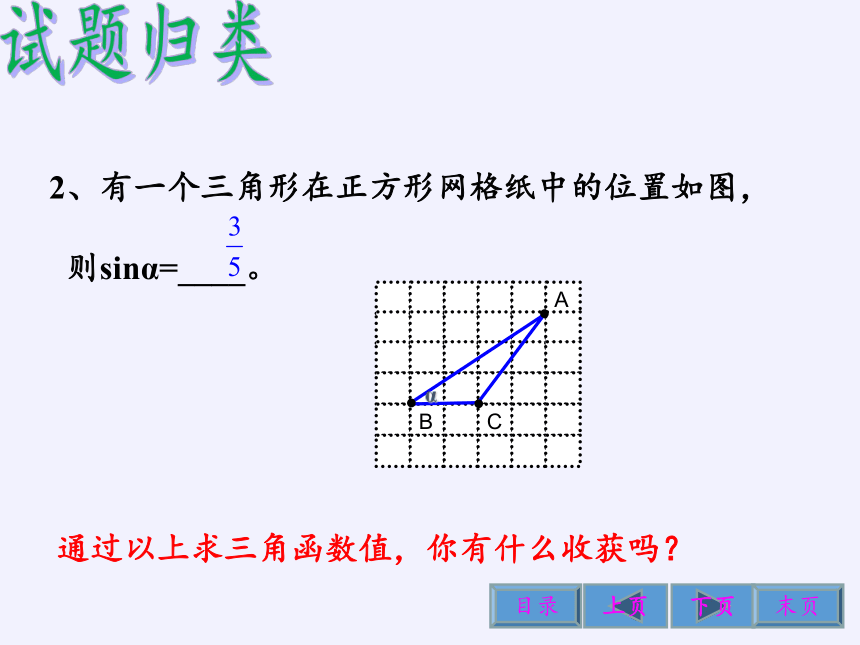
2、有一个三角形在正方形网格纸中的位置如图,
则sinα=____。
B
C
A
α
试题归类
通过以上求三角函数值,你有什么收获吗?
下页
上页
目录
末页
当∠A为锐角,且cosA= ,那么( )
(A)0°<∠A< 30 ° (B) 30°<∠A<45°
(C)45°<∠A<60 ° (D) 60°<∠A< 90 °
D
第2类:侧重对特殊锐角的三角函数值灵活把握
试题归类
你想知道是怎样分析吗?
下页
上页
目录
末页
例1、如图,四边形ABCD中,AD⊥CD,AB=13,
BC=12,CD=3,AD=4,则sinB=___________,
S四边形ABCD=___________。
思维训练
你知道连接AC有什么作用吗?
下页
上页
目录
末页
例2. 如图,太阳光与地面成60度角,一棵倾斜的大树AB与地面成30度角,这时测得大树在地面上的影长为10m,请你求出大树的高.
A
B
C
30°
地面
太阳光线
60°
10
AD的长
D
思维训练
下页
上页
目录
末页
解直角三角形步骤和注意
A
B
C
30°
地面
太阳光线
60°
D
10
∟
解:过A作AD⊥BC于D,
设AD= x米.
在Rt△ACD中,tan60°=
∴CD=
x.
BD= 10+
x.
在Rt△ABD中,tan30°=
BD
AD
∴ =
BD
AD
X =5
答:树高 5 米。.
下页
上页
目录
末页
例3、外国船只,除特许外,不得进入我国海洋100海里以内的区域。如图,设A、B是我们的观察站,A和B之间的距离为160海里,海岸线是过A、B的一条直线。一外国船只在P点,在A点测得∠BAP=45°,同时在B点测得∠ABP=60°,问此时是否要向外国船只发出警告,令其退出我国海域.
A
B
P
⌒
⌒
45°
60°
┓
C
思维训练
下页
上页
目录
末页
1. 如图,在△ABC中,已知AC=6,∠C=75°,∠B=45°,求△ABC的面积。
75°
A
B
C
D
⌒
450
⌒
⌒
60°
┓
6
讨论交流
你知道如何构造直角三角形吗?
下页
上页
目录
末页
一渔船上的渔民在A处看见灯塔在北偏东60°方向,这艘渔船以28海里/时的速度向正东航行,半小时到B处.在B处看见灯塔M在北偏东15°方向,求此时灯塔M与渔船的距离 ?
创新应用
下页
上页
目录
末页
已知在△ABC中,AB+AC=9,AB和AC的夹角为30度,
设当AB=x时,△ABC面积为S
(1)求S关于x的函数解析式.
(2)问何时△ABC面积最大 最大面积是多少
提高题
下页
上页
目录
末页
拓展提高
中考练兵
下页
上页
目录
末页
中考练兵
下页
上页
目录
末页
中考练兵
下页
上页
目录
末页
中考练兵
下页
上页
目录
末页
再 见
谢 谢
解直角三角形
解直角三角形复习
生活问题
一
知识梳理
二
试题归类
三
思维训练
四
讨论交流
五
下页
上页
首页
末页
中考练兵
六
如果∠A是直角三角形ABC的一个锐角, 则有
∠A的对边
∠A的邻边
tanA
cosA
∠A的邻边
∠A的对边
斜边
sinA
斜边
B
C
A
∠A的对边
∠A的邻边
斜边
锐角A的正弦、余弦、和正切统称∠A的三角函数.
1.锐角三角函数
知识梳理
下页
上页
目录
末页
30°,45°,60°的三角函数值
30° 45° 60°
sina
cosa
tana
1
300
┌
┌
450
450
600
1
2
1
1
2.特殊角的三角函数值
0°,90°的三角函数值你知道吗?
知识梳理
下页
上页
目录
末页
三边之间的关系
a2+b2=c2(勾股定理);
锐角之间的关系
∠ A+ ∠ B= 90
边角之间的关系(锐角三角函数)
tanA =
a
b
sinA =
a
c
cosA=
b
c
A
C
B
a
b
c
3.解直角三角形的依据
知识梳理
下页
上页
目录
末页
(09·滨州)某楼梯侧面视图如图,其中AB=4m,∠BAC=30°,∠C=90°,因某种活动,要求铺设红色地毯,则在AB段楼梯所铺地毯的长应 。
B
C
A
生活问题
下页
上页
目录
末页
第1类:侧重在网格背景下求三角函数值
1、(08·襄樊)在正方形网格中,点A、B、C、D的位置如图所示,则cosB的值为( )
A、 B、 C、 D、
等腰直角三角形
试题归类
下页
上页
目录
末页
2、有一个三角形在正方形网格纸中的位置如图,
则sinα=____。
B
C
A
α
试题归类
通过以上求三角函数值,你有什么收获吗?
下页
上页
目录
末页
当∠A为锐角,且cosA= ,那么( )
(A)0°<∠A< 30 ° (B) 30°<∠A<45°
(C)45°<∠A<60 ° (D) 60°<∠A< 90 °
D
第2类:侧重对特殊锐角的三角函数值灵活把握
试题归类
你想知道是怎样分析吗?
下页
上页
目录
末页
例1、如图,四边形ABCD中,AD⊥CD,AB=13,
BC=12,CD=3,AD=4,则sinB=___________,
S四边形ABCD=___________。
思维训练
你知道连接AC有什么作用吗?
下页
上页
目录
末页
例2. 如图,太阳光与地面成60度角,一棵倾斜的大树AB与地面成30度角,这时测得大树在地面上的影长为10m,请你求出大树的高.
A
B
C
30°
地面
太阳光线
60°
10
AD的长
D
思维训练
下页
上页
目录
末页
解直角三角形步骤和注意
A
B
C
30°
地面
太阳光线
60°
D
10
∟
解:过A作AD⊥BC于D,
设AD= x米.
在Rt△ACD中,tan60°=
∴CD=
x.
BD= 10+
x.
在Rt△ABD中,tan30°=
BD
AD
∴ =
BD
AD
X =5
答:树高 5 米。.
下页
上页
目录
末页
例3、外国船只,除特许外,不得进入我国海洋100海里以内的区域。如图,设A、B是我们的观察站,A和B之间的距离为160海里,海岸线是过A、B的一条直线。一外国船只在P点,在A点测得∠BAP=45°,同时在B点测得∠ABP=60°,问此时是否要向外国船只发出警告,令其退出我国海域.
A
B
P
⌒
⌒
45°
60°
┓
C
思维训练
下页
上页
目录
末页
1. 如图,在△ABC中,已知AC=6,∠C=75°,∠B=45°,求△ABC的面积。
75°
A
B
C
D
⌒
450
⌒
⌒
60°
┓
6
讨论交流
你知道如何构造直角三角形吗?
下页
上页
目录
末页
一渔船上的渔民在A处看见灯塔在北偏东60°方向,这艘渔船以28海里/时的速度向正东航行,半小时到B处.在B处看见灯塔M在北偏东15°方向,求此时灯塔M与渔船的距离 ?
创新应用
下页
上页
目录
末页
已知在△ABC中,AB+AC=9,AB和AC的夹角为30度,
设当AB=x时,△ABC面积为S
(1)求S关于x的函数解析式.
(2)问何时△ABC面积最大 最大面积是多少
提高题
下页
上页
目录
末页
拓展提高
中考练兵
下页
上页
目录
末页
中考练兵
下页
上页
目录
末页
中考练兵
下页
上页
目录
末页
中考练兵
下页
上页
目录
末页
再 见
谢 谢
