沪科版数学八年级上册 14.2直角三角形全等的判定 课件(共15张PPT)
文档属性
| 名称 | 沪科版数学八年级上册 14.2直角三角形全等的判定 课件(共15张PPT) |  | |
| 格式 | ppt | ||
| 文件大小 | 1.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-12-27 13:17:09 | ||
图片预览





文档简介
(共15张PPT)
14.2 三角形全等的判定5
——两个直角三角形全等的判定
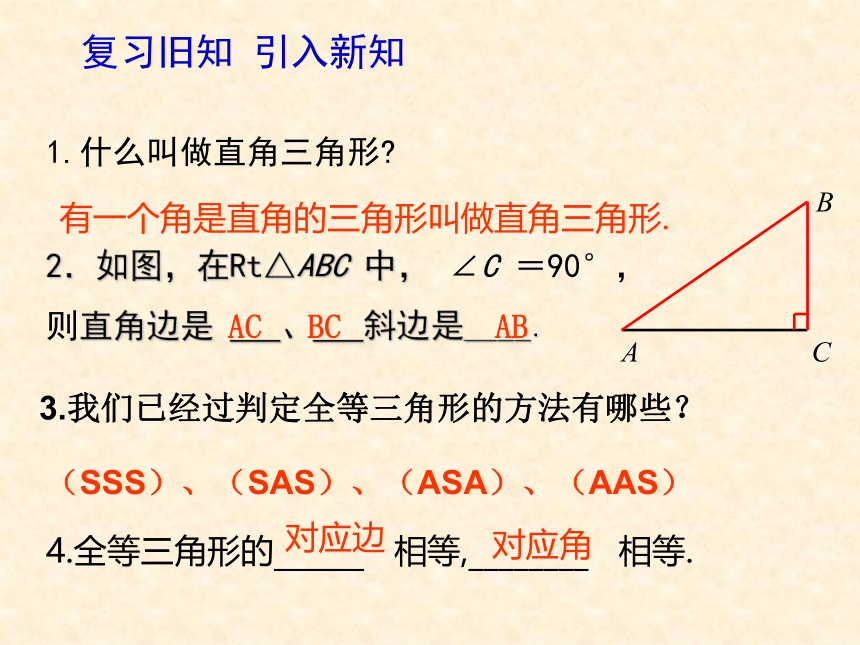
3.我们已经过判定全等三角形的方法有哪些?
(SSS)、(SAS)、(ASA)、(AAS)
1.什么叫做直角三角形
复习旧知 引入新知
有一个角是直角的三角形叫做直角三角形.
A
B
C
2.如图,在Rt△ABC 中, ∠C =90°,
则直角边是 、 斜边是____.
AC
BC
AB
4.全等三角形的______ 相等,________ 相等.
对应边
对应角
5.用上述四种方法来判定两个直角三角形全等,思考下列问题?看一看用的是哪种方法。
A
B
C
A′
B′
C′
如图,在Rt△ABC与Rt△A'B'C' 中,
∠C=∠C'=90°,
(1)若 AC=A'C',BC=B'C',
△ABC≌△A'B'C' ( ).
(2)若∠A=∠A',AC=A'C',
则△ABC≌△A'B'C' ( ).
(3)若∠A=∠A',BC=B'C',
则△ABC≌△A'B'C' ( ).
SAS
ASA
AAS
A
B
C
A′
B′
C′
如图,在Rt△ABC与Rt△A'B'C' 中,
∠C=∠C'=90°,
(4)若 AC=A'C',BC=B'C',AB=A'B'
△ABC≌△A'B'C' ( ).
(5)若 AC=A'C',AB=A'B'
△ABC和△A'B'C'全等吗?
能否用上述四种方法判定
SSS
5.用上述四种方法来判定两个直角三角形全等,思考下列问题?看一看用的是哪种方法。
不能
未知
画图,叠放,观察,总结:
已知:Rt△ABC ,∠C﹦90°求作:Rt△A′B′C′
使①∠C′﹦90°,②A′C′﹦AC,③A′B′﹦AB
(1)你能试着画出来吗?
(2)把画好的Rt△A′B′C′放到Rt△ABC上,它们完全重合吗?你能发现什么规律?
动手实践 探索规律
作图思路:
1.① ② ③
2.② ① ③
3.① ③ ②
4.② ③ ①
5.③ ① ②
6.③ ② ①
√
√
×
×
×
×
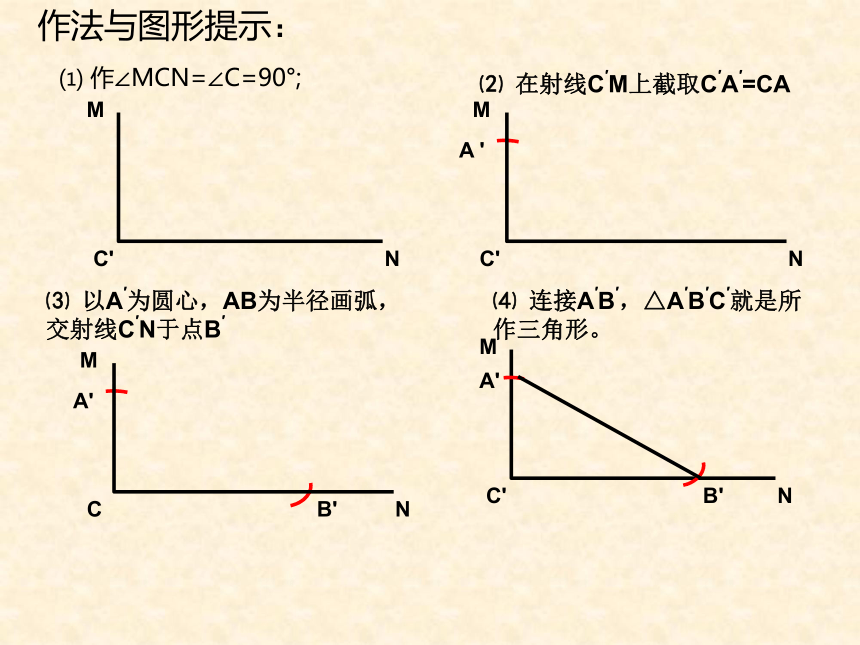
作法与图形提示:
⑴ 作∠MCN=∠C=90°;
⑵ 在射线C′M上截取C′A′=CA
A '
⑶ 以A′为圆心,AB为半径画弧,交射线C′N于点B′
A'
B'
⑷ 连接A′B′,△A′B′C′就是所作三角形。
C'
M
N
C'
M
N
C
M
N
C'
M
N
A'
B'
斜边、直角边定理
有斜边和一条直角边对应相等的两个直角三角形全等.
简写成“斜边、直角边”
或“HL”
总结规律 运用新知
斜边、直角边定理 (HL)推理格式
A
B
C
A ′
B′
C ′
∴在Rt△ABC和Rt△ 中
AB=
BC=
∴Rt△ABC≌
∵∠C=∠C′=90°
有斜边和一条直角边对应相等的两个直角三角形全等.
例:如图,∠BAC=∠CDB=900, AC﹦DB,求证:AB﹦DC
B
C
D
A
证明: ∵∠BAC=∠CDB=900(已知)
∴ΔBAC,ΔCDB都是直角三角形.
AC=DB,(已知)
BC=BC.(公共边)
∴Rt△ABC≌Rt△DCB (HL).
∴ AB﹦DC(全等三角形对应边相等)
在 Rt△ABC 和 Rt△DCB 中,
分析:
例题变式;如图,∠BAC=∠CDB=900,请你再添加一个条件
使△ABC≌△DCB ,并说明判定依据?
B
C
D
A
1.AB=DC (HL)
2.AC=DB (HL)
3.∠ABC=∠DCB (AAS)
4.∠ACB=∠DBC (AAS)
A
B
C
D
A
B
C
D
2.已知:如图, △ABC中,AB=AC,AD是高
求证:BD=CD ;∠BAD=∠CAD
1. 已知:如图,AC=AD,∠C,∠D是直角,
求证:BC=BD
C
D
A
B
巩固练习
3.课本P109练习 1,2
1、证明:∵∠C,∠D是直角(已知)
∴ΔABC,ΔADB都是直角三角形.
在Rt△ACB和Rt△ADB中
AB=AB,(公共边)
AC=AD.(已知)
∴ Rt△ACB≌Rt△ADB (HL).
∴BC=BD
(全等三角形对应边相等).
2.证明:∵AD是高
∴∠ADB=∠ADC=90°
在Rt△ADB和Rt△ADC中
AB=AC(已知)
AD=AD(公共边)
∴ Rt△ADB≌Rt△ADC(HL)
∴BD=CD,∠BAD=∠CAD
(全等三角形对应边相等,对应角相等)
小结
直角三角形全等的判定
一般三角形全等的判定
“SAS”
“ ASA ”
“ AAS ”
“ SSS ”
“ SAS ”
“ ASA ”
“ AAS ”
“ HL ”
灵活运用各种方法证明直角三角形全等
“ SSS ”
书面作业:P109 3
P112 9
课后体会:学完判定全等三角形的条件后,你 有什么收获?
我们的生活离不开数学,我们要做生活的有心人。
再 见
14.2 三角形全等的判定5
——两个直角三角形全等的判定
3.我们已经过判定全等三角形的方法有哪些?
(SSS)、(SAS)、(ASA)、(AAS)
1.什么叫做直角三角形
复习旧知 引入新知
有一个角是直角的三角形叫做直角三角形.
A
B
C
2.如图,在Rt△ABC 中, ∠C =90°,
则直角边是 、 斜边是____.
AC
BC
AB
4.全等三角形的______ 相等,________ 相等.
对应边
对应角
5.用上述四种方法来判定两个直角三角形全等,思考下列问题?看一看用的是哪种方法。
A
B
C
A′
B′
C′
如图,在Rt△ABC与Rt△A'B'C' 中,
∠C=∠C'=90°,
(1)若 AC=A'C',BC=B'C',
△ABC≌△A'B'C' ( ).
(2)若∠A=∠A',AC=A'C',
则△ABC≌△A'B'C' ( ).
(3)若∠A=∠A',BC=B'C',
则△ABC≌△A'B'C' ( ).
SAS
ASA
AAS
A
B
C
A′
B′
C′
如图,在Rt△ABC与Rt△A'B'C' 中,
∠C=∠C'=90°,
(4)若 AC=A'C',BC=B'C',AB=A'B'
△ABC≌△A'B'C' ( ).
(5)若 AC=A'C',AB=A'B'
△ABC和△A'B'C'全等吗?
能否用上述四种方法判定
SSS
5.用上述四种方法来判定两个直角三角形全等,思考下列问题?看一看用的是哪种方法。
不能
未知
画图,叠放,观察,总结:
已知:Rt△ABC ,∠C﹦90°求作:Rt△A′B′C′
使①∠C′﹦90°,②A′C′﹦AC,③A′B′﹦AB
(1)你能试着画出来吗?
(2)把画好的Rt△A′B′C′放到Rt△ABC上,它们完全重合吗?你能发现什么规律?
动手实践 探索规律
作图思路:
1.① ② ③
2.② ① ③
3.① ③ ②
4.② ③ ①
5.③ ① ②
6.③ ② ①
√
√
×
×
×
×
作法与图形提示:
⑴ 作∠MCN=∠C=90°;
⑵ 在射线C′M上截取C′A′=CA
A '
⑶ 以A′为圆心,AB为半径画弧,交射线C′N于点B′
A'
B'
⑷ 连接A′B′,△A′B′C′就是所作三角形。
C'
M
N
C'
M
N
C
M
N
C'
M
N
A'
B'
斜边、直角边定理
有斜边和一条直角边对应相等的两个直角三角形全等.
简写成“斜边、直角边”
或“HL”
总结规律 运用新知
斜边、直角边定理 (HL)推理格式
A
B
C
A ′
B′
C ′
∴在Rt△ABC和Rt△ 中
AB=
BC=
∴Rt△ABC≌
∵∠C=∠C′=90°
有斜边和一条直角边对应相等的两个直角三角形全等.
例:如图,∠BAC=∠CDB=900, AC﹦DB,求证:AB﹦DC
B
C
D
A
证明: ∵∠BAC=∠CDB=900(已知)
∴ΔBAC,ΔCDB都是直角三角形.
AC=DB,(已知)
BC=BC.(公共边)
∴Rt△ABC≌Rt△DCB (HL).
∴ AB﹦DC(全等三角形对应边相等)
在 Rt△ABC 和 Rt△DCB 中,
分析:
例题变式;如图,∠BAC=∠CDB=900,请你再添加一个条件
使△ABC≌△DCB ,并说明判定依据?
B
C
D
A
1.AB=DC (HL)
2.AC=DB (HL)
3.∠ABC=∠DCB (AAS)
4.∠ACB=∠DBC (AAS)
A
B
C
D
A
B
C
D
2.已知:如图, △ABC中,AB=AC,AD是高
求证:BD=CD ;∠BAD=∠CAD
1. 已知:如图,AC=AD,∠C,∠D是直角,
求证:BC=BD
C
D
A
B
巩固练习
3.课本P109练习 1,2
1、证明:∵∠C,∠D是直角(已知)
∴ΔABC,ΔADB都是直角三角形.
在Rt△ACB和Rt△ADB中
AB=AB,(公共边)
AC=AD.(已知)
∴ Rt△ACB≌Rt△ADB (HL).
∴BC=BD
(全等三角形对应边相等).
2.证明:∵AD是高
∴∠ADB=∠ADC=90°
在Rt△ADB和Rt△ADC中
AB=AC(已知)
AD=AD(公共边)
∴ Rt△ADB≌Rt△ADC(HL)
∴BD=CD,∠BAD=∠CAD
(全等三角形对应边相等,对应角相等)
小结
直角三角形全等的判定
一般三角形全等的判定
“SAS”
“ ASA ”
“ AAS ”
“ SSS ”
“ SAS ”
“ ASA ”
“ AAS ”
“ HL ”
灵活运用各种方法证明直角三角形全等
“ SSS ”
书面作业:P109 3
P112 9
课后体会:学完判定全等三角形的条件后,你 有什么收获?
我们的生活离不开数学,我们要做生活的有心人。
再 见
