2021-2022学年人教版八年级上册数学期末专题 第十五章分式计算与分式方程课件(16张ppt)
文档属性
| 名称 | 2021-2022学年人教版八年级上册数学期末专题 第十五章分式计算与分式方程课件(16张ppt) |  | |
| 格式 | zip | ||
| 文件大小 | 1.6MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-12-27 14:01:54 | ||
图片预览






文档简介
(共16张PPT)
分式计算和分式方程专题
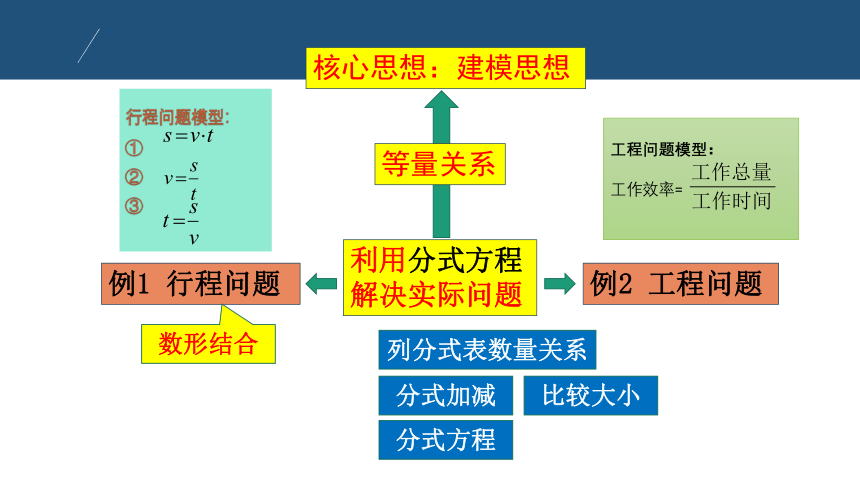
利用分式方程解决实际问题
例2 工程问题
例1 行程问题
核心思想:建模思想
等量关系
行程问题模型:
①
②
③
工程问题模型:
工作效率=
数形结合
比较大小
分式加减
列分式表数量关系
分式方程
01
典型例题
典型例题1
2021年11月4日,大连庄河市新冠疫情爆发,大连政府迅速组建第一支医疗队
以 v km/h的速度前往庄河支援,由于疫情发展迅速,又迅速组建第二支医疗队以比之前速度增加 20km/h 的速度前往庄河支援,大连与庄河两地相距 n km.
(1)第一支医疗队速度______________,第二支医疗队速度_________________.
(2)第二支医疗队时间比第一支医疗队时间多多少?
V km/h
(V+20)km/h
行程问题模型:
①
②
③
教材P153-例4、P147-13
01
典型例题
典型例题1
(3)大连与庄河两地相距160 km,第一支医疗队出发40 km后,第二医疗队也出发前往庄河,两支医疗队同时到达庄河,求两支医疗队速度.
(4)第一支医疗队出发a km后,第二医疗队也出发前往庄河,两支医疗队同时到达庄河,求两支医疗队速度(用含a、n的式子表示)
一队
庄
河
160 km
40 km
t h
t h
二队
大
连
a km
n km
01
典型例题
【平行练习】
由于疫情严重,大连政府紧急增派甲、乙两医疗队分别从距庄河m km和n km的两地同时出发前往庄河,甲、乙两医疗队的速度比是4:3.,甲医疗队比乙医疗队提前5分钟到达.
(1)当m=150km,n=120km时,求甲、乙两医疗队的速度各是多少.
(2)当甲、乙两支医疗队的路程和为300km时,求甲、乙两医疗队的速度各是多少
(用含m的式子表示).
教材P154-3
转化思想
01
典型例题
【变式训练】
大连与庄河两地相距n km,现有两支医疗队同时从大连出发,为尽快到庄时进行支援,第一支医疗队前一半路程以v km/h的速度行驶,后一半路程提速30km/h,第二支医疗队前一半时间以(v +20)km/h的速度行驶,后一半时间提速20km/h,
(1)分别求出两支医疗队到达庄河的时间
(2)判定哪一支医疗队先到达庄河,并说明理由
作差法:
01
典型例题
典型例题2
在本轮疫情中,泉水地区共有人数a人,如果安排甲医疗队100名医护人员进行核算检测,需要m天完成;如果安排乙医疗队100名医护人员进行核算检测,要比甲医疗队提前3天完成,乙医疗队的工作效率是甲医疗队的多少倍?
工程问题模型:
工作效率=
教材P137-例3、P139-问题3
01
典型例题
【变式训练1】
众志成城抗疫情,核酸检测与时间赛跑,为尽快完成“应检尽检”工作,我市两个医疗队共同参与某一社区的核算检测工作,第一支医疗队单独检测1天完成社区总人数的,这时增加第二支医疗队,两队又共同检测了1天,完成该社区全员核酸检测工作。哪个医疗队检测速度快?
工作效率叠加
教材P152-例3
等量关系:
工作总量=1
01
典型例题
【变式训练2】
在本轮疫情中,甲医疗队按照上级要求,进入泉水K3区进行核酸检测工作,第一天核酸检测时每名医护人员每小时可以检测y人,20小时完成m人的检测工作;K3区全体居民积极配合医护人员核酸检测工作,该医疗队在第二天的核酸检测中,每名医护人员每小时可增加检测a人,第二天检测18小时,比第一天多检测100人,此时恰好完成K3区的全员核酸检测工作。
(1)甲医疗队有_________名医护人员,K3区共有 __________位居民
(2)①当m=600,a=8时,求开始阶段每名医护人员每小时可以检测多少人?
②求开始阶段和后一阶段每名医护人员每小时各可以检测多少人?
(用含m,a的式子表示).
(2m+100)
等量关系:
医护人员人数不变
教材P147-11
01
典型例题
【变式训练2】
(3)由于疫情严重,需要尽快完成K3区的核酸检测工作,现安排甲、乙两医疗队共同完成检测工作,甲医疗队单独完成需要n小时,乙医疗队比甲医疗队单独完成少用1小时,两支医疗队一起完成,需要多长时间?
(4)由于疫情严重,需要在10小时内完成K3区的核酸检测工作,在(3)的条件下,甲、乙两支医疗队工作3小时后,增加丙医疗队参加检测工作,求丙医疗队单独完成需要多少小时?
工作效率叠加
01
典型例题
【课堂检测】
在本轮疫情中,甲医疗队按照上级要求,进入泉水K3区进行核酸检测工作,开始阶段m名医护人员a小时可以完成p人的检测工作;后一阶段K3区全体居民积极配合医护人员核酸检测工作,医护人员检查加快。
(1)开始阶段每名医护人员每小时可以检测_____________人
(2)后一阶段医护人员(a+2)小时可以完成3p人的核酸检测工作,求后一阶段每名医护人员每小时比原来多检测检测多少人?
01
典型例题
课前练习
利用分式方程解决实际问题
德育渗透
建模思想
数学应用意识
数学核心素养
实际情景
01
典型例题
【课后作业】
1、某市为了做好“全国文明城市”验收工作,计划对市区S米长的道路进行改造,现
安排甲、乙两个工程队进行施工.
(1)已知甲工程队改造360米的道路与乙工程队改造300米的道路所用时间相同.若甲工程队每天比乙工程队多改造30米,求甲、乙两工程队每天改造道路的长度各是多少米;
(2)若甲工程队每天可以改造a米道路,乙工程队每天可以改造b米道路,(其中
a≠b).现在有两种施工改造方案:
方案一:前 S米的道路由甲工程队改造,后 S米的道路由乙工程队改造;
方案二:完成整个道路改造,前一半时间由甲工程队改造,后一半时间由乙工程队改造.
根据上述描述,请你判断哪种改造方案所用时间少?并说明理由.
01
典型例题
【课后作业】
2、甲、乙两人两次同时在同一家超市采购货物(假设两次采购货物的单价不相同),甲每次采购货物100千克,乙每次采购货物用去100元.
(1)假设、分别表示两次采购货物时的单价(单位:元/千克),试用含、的式子表示:甲
两次采购货物共需付款________元,乙两次共购买________千克货物;
(2)请你判断甲、乙两人采购货物的方式哪一个的平均单价低,并说明理由.
01
典型例题
【课后作业】
3、某小麦改良品种后,平均每公顷增加产量a吨,原来产m吨小麦的一块土地,现在的总
产量增加了20吨.
(1)当a=0.8,m=100时,原来和现在小麦的平均每公顷产量各是多少?
(2)请直接接写出原来小麦的平均每公顷产量是__________吨,现在小麦的平均每公
顷产量是__________吨;(用含a、m的式子表示)
(3)在这块土地上,小麦的改良品种成熟后,甲组收割完需n小时,乙组比甲组少用0.5小时就能收割完,求两组一起收割完这块麦田需要多少小时?
感谢聆听!
分式计算和分式方程专题
利用分式方程解决实际问题
例2 工程问题
例1 行程问题
核心思想:建模思想
等量关系
行程问题模型:
①
②
③
工程问题模型:
工作效率=
数形结合
比较大小
分式加减
列分式表数量关系
分式方程
01
典型例题
典型例题1
2021年11月4日,大连庄河市新冠疫情爆发,大连政府迅速组建第一支医疗队
以 v km/h的速度前往庄河支援,由于疫情发展迅速,又迅速组建第二支医疗队以比之前速度增加 20km/h 的速度前往庄河支援,大连与庄河两地相距 n km.
(1)第一支医疗队速度______________,第二支医疗队速度_________________.
(2)第二支医疗队时间比第一支医疗队时间多多少?
V km/h
(V+20)km/h
行程问题模型:
①
②
③
教材P153-例4、P147-13
01
典型例题
典型例题1
(3)大连与庄河两地相距160 km,第一支医疗队出发40 km后,第二医疗队也出发前往庄河,两支医疗队同时到达庄河,求两支医疗队速度.
(4)第一支医疗队出发a km后,第二医疗队也出发前往庄河,两支医疗队同时到达庄河,求两支医疗队速度(用含a、n的式子表示)
一队
庄
河
160 km
40 km
t h
t h
二队
大
连
a km
n km
01
典型例题
【平行练习】
由于疫情严重,大连政府紧急增派甲、乙两医疗队分别从距庄河m km和n km的两地同时出发前往庄河,甲、乙两医疗队的速度比是4:3.,甲医疗队比乙医疗队提前5分钟到达.
(1)当m=150km,n=120km时,求甲、乙两医疗队的速度各是多少.
(2)当甲、乙两支医疗队的路程和为300km时,求甲、乙两医疗队的速度各是多少
(用含m的式子表示).
教材P154-3
转化思想
01
典型例题
【变式训练】
大连与庄河两地相距n km,现有两支医疗队同时从大连出发,为尽快到庄时进行支援,第一支医疗队前一半路程以v km/h的速度行驶,后一半路程提速30km/h,第二支医疗队前一半时间以(v +20)km/h的速度行驶,后一半时间提速20km/h,
(1)分别求出两支医疗队到达庄河的时间
(2)判定哪一支医疗队先到达庄河,并说明理由
作差法:
01
典型例题
典型例题2
在本轮疫情中,泉水地区共有人数a人,如果安排甲医疗队100名医护人员进行核算检测,需要m天完成;如果安排乙医疗队100名医护人员进行核算检测,要比甲医疗队提前3天完成,乙医疗队的工作效率是甲医疗队的多少倍?
工程问题模型:
工作效率=
教材P137-例3、P139-问题3
01
典型例题
【变式训练1】
众志成城抗疫情,核酸检测与时间赛跑,为尽快完成“应检尽检”工作,我市两个医疗队共同参与某一社区的核算检测工作,第一支医疗队单独检测1天完成社区总人数的,这时增加第二支医疗队,两队又共同检测了1天,完成该社区全员核酸检测工作。哪个医疗队检测速度快?
工作效率叠加
教材P152-例3
等量关系:
工作总量=1
01
典型例题
【变式训练2】
在本轮疫情中,甲医疗队按照上级要求,进入泉水K3区进行核酸检测工作,第一天核酸检测时每名医护人员每小时可以检测y人,20小时完成m人的检测工作;K3区全体居民积极配合医护人员核酸检测工作,该医疗队在第二天的核酸检测中,每名医护人员每小时可增加检测a人,第二天检测18小时,比第一天多检测100人,此时恰好完成K3区的全员核酸检测工作。
(1)甲医疗队有_________名医护人员,K3区共有 __________位居民
(2)①当m=600,a=8时,求开始阶段每名医护人员每小时可以检测多少人?
②求开始阶段和后一阶段每名医护人员每小时各可以检测多少人?
(用含m,a的式子表示).
(2m+100)
等量关系:
医护人员人数不变
教材P147-11
01
典型例题
【变式训练2】
(3)由于疫情严重,需要尽快完成K3区的核酸检测工作,现安排甲、乙两医疗队共同完成检测工作,甲医疗队单独完成需要n小时,乙医疗队比甲医疗队单独完成少用1小时,两支医疗队一起完成,需要多长时间?
(4)由于疫情严重,需要在10小时内完成K3区的核酸检测工作,在(3)的条件下,甲、乙两支医疗队工作3小时后,增加丙医疗队参加检测工作,求丙医疗队单独完成需要多少小时?
工作效率叠加
01
典型例题
【课堂检测】
在本轮疫情中,甲医疗队按照上级要求,进入泉水K3区进行核酸检测工作,开始阶段m名医护人员a小时可以完成p人的检测工作;后一阶段K3区全体居民积极配合医护人员核酸检测工作,医护人员检查加快。
(1)开始阶段每名医护人员每小时可以检测_____________人
(2)后一阶段医护人员(a+2)小时可以完成3p人的核酸检测工作,求后一阶段每名医护人员每小时比原来多检测检测多少人?
01
典型例题
课前练习
利用分式方程解决实际问题
德育渗透
建模思想
数学应用意识
数学核心素养
实际情景
01
典型例题
【课后作业】
1、某市为了做好“全国文明城市”验收工作,计划对市区S米长的道路进行改造,现
安排甲、乙两个工程队进行施工.
(1)已知甲工程队改造360米的道路与乙工程队改造300米的道路所用时间相同.若甲工程队每天比乙工程队多改造30米,求甲、乙两工程队每天改造道路的长度各是多少米;
(2)若甲工程队每天可以改造a米道路,乙工程队每天可以改造b米道路,(其中
a≠b).现在有两种施工改造方案:
方案一:前 S米的道路由甲工程队改造,后 S米的道路由乙工程队改造;
方案二:完成整个道路改造,前一半时间由甲工程队改造,后一半时间由乙工程队改造.
根据上述描述,请你判断哪种改造方案所用时间少?并说明理由.
01
典型例题
【课后作业】
2、甲、乙两人两次同时在同一家超市采购货物(假设两次采购货物的单价不相同),甲每次采购货物100千克,乙每次采购货物用去100元.
(1)假设、分别表示两次采购货物时的单价(单位:元/千克),试用含、的式子表示:甲
两次采购货物共需付款________元,乙两次共购买________千克货物;
(2)请你判断甲、乙两人采购货物的方式哪一个的平均单价低,并说明理由.
01
典型例题
【课后作业】
3、某小麦改良品种后,平均每公顷增加产量a吨,原来产m吨小麦的一块土地,现在的总
产量增加了20吨.
(1)当a=0.8,m=100时,原来和现在小麦的平均每公顷产量各是多少?
(2)请直接接写出原来小麦的平均每公顷产量是__________吨,现在小麦的平均每公
顷产量是__________吨;(用含a、m的式子表示)
(3)在这块土地上,小麦的改良品种成熟后,甲组收割完需n小时,乙组比甲组少用0.5小时就能收割完,求两组一起收割完这块麦田需要多少小时?
感谢聆听!
