2021—2022学年沪科版九年级数学上册23.1锐角的三角函数(第3课时特殊角的三角函数值)课件(22张)
文档属性
| 名称 | 2021—2022学年沪科版九年级数学上册23.1锐角的三角函数(第3课时特殊角的三角函数值)课件(22张) |

|
|
| 格式 | zip | ||
| 文件大小 | 624.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-12-27 15:49:35 | ||
图片预览



文档简介
(共22张PPT)
第3课时 特殊角的三角函数值
23.1锐角的三角函数
第23章 解直三角形
沪科版数学九年级上
复习:
1.锐角三角函数的定义
在 中,
∠A的余弦 :
∠A的正弦:
b
A
B
C
a
┌
c
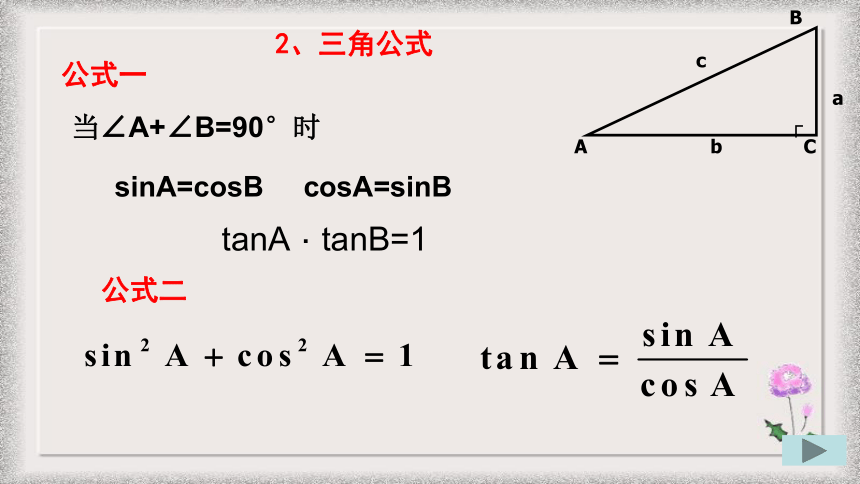
当∠A+∠B=90°时
公式二
2、三角公式
tanA . tanB=1
公式一
sinA=cosB cosA=sinB
Sin30°=
cos30°=
tan30°=
新知探究
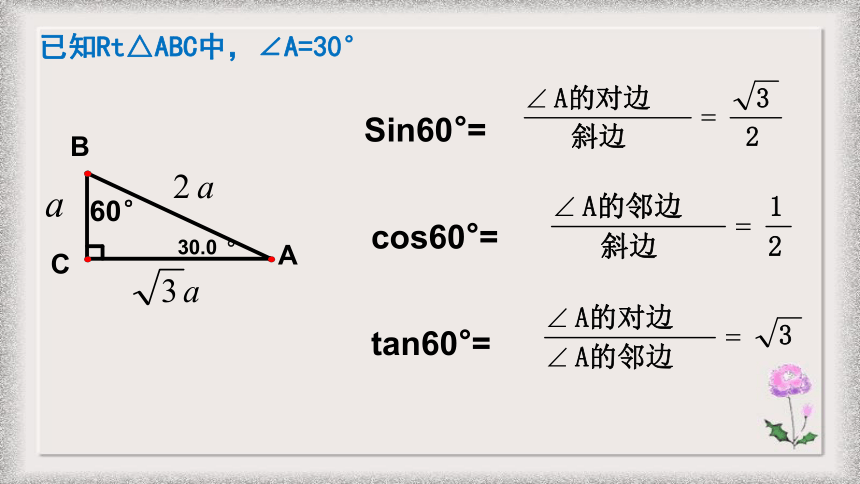
已知Rt△ABC中,∠A=30°
Sin60°=
cos60°=
tan60°=
60°
已知Rt△ABC中,∠A=30°
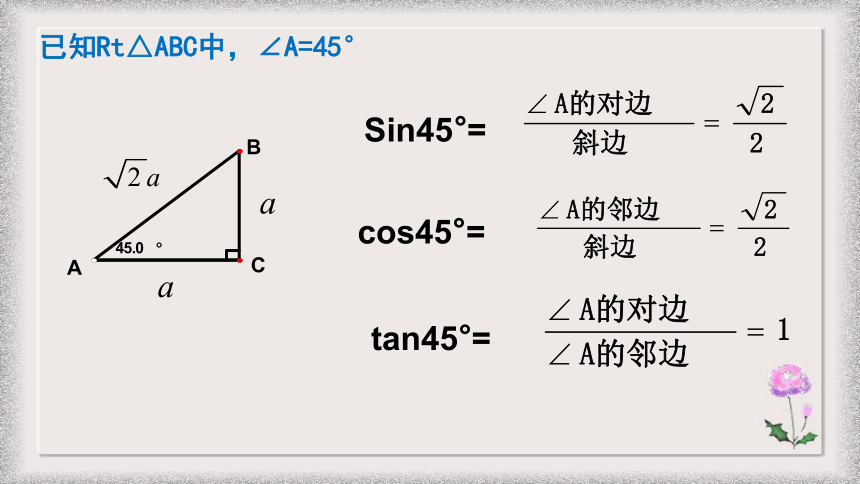
cos45°=
tan45°=
Sin45°=
已知Rt△ABC中,∠A=45°
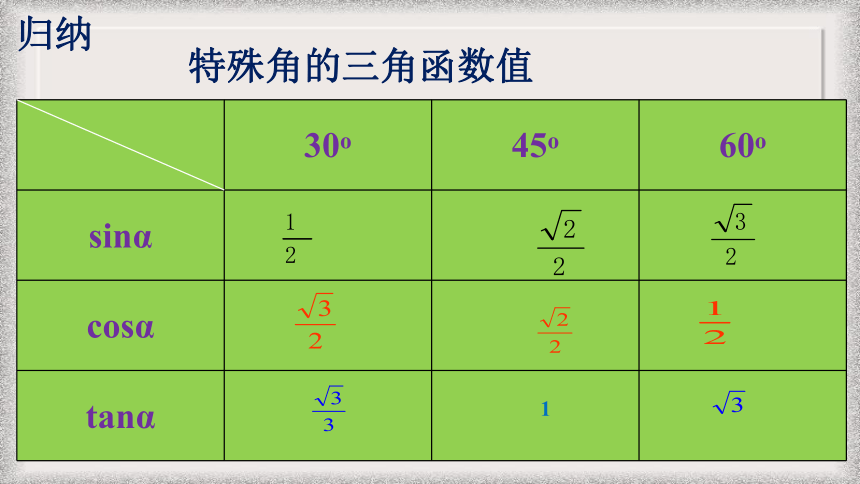
归纳
特殊角的三角函数值
30o 45o 60o
sinα
cosα
tanα
1
30o 45o 60o
sinα
cosα
tanα
1
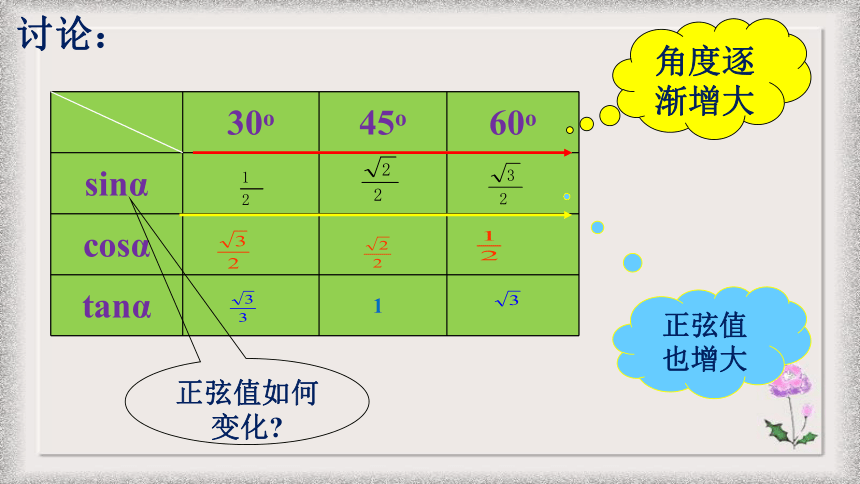
角度逐渐增大
正弦值如何变化
正弦值也增大
讨论:
30o 45o 60o
sinα
cosα
tanα
1
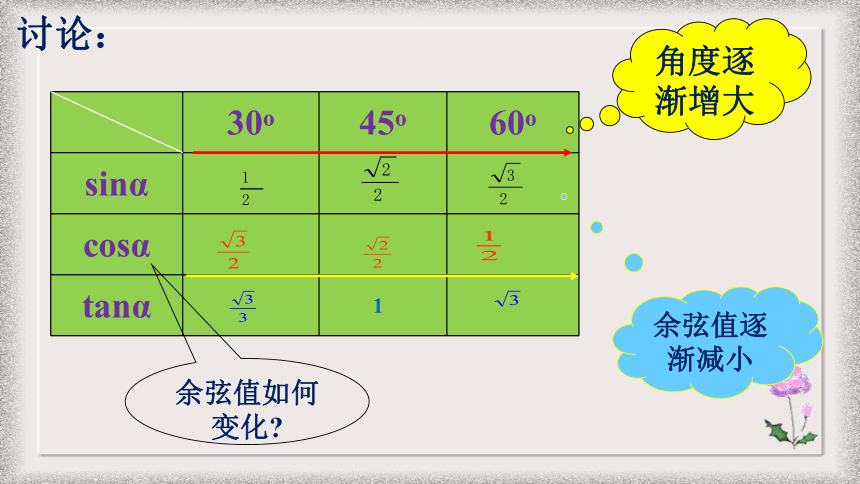
角度逐渐增大
余弦值如何变化
余弦值逐渐减小
讨论:
30o 45o 60o
sinα
cosα
tanα
1
角度逐渐增大
正切值如何变化
正切值也增大
讨论:
30o 45o 60o
sinα
cosα
tanα
1
讨论:
锐角A的正弦值、余弦值有无变化范围?
0< sinA<1
0三角函数的增减性
(1)当 时,α的正弦值随着角度的增大而增大。
(3)当 时,α的正切值随着角度的增大而增大。
(2)当 时, α的余弦值随着角度的增大而减小。
归纳
例1、求下列各式的值:
利用特殊的三角函数值进行计算
新知应用
例2 如图,在Rt△ABC中,∠C=90°,AC= ,BC= ,求∠A的度数。
A
C
B
解:在Rt△ABC
∵tanA=
∴∠A=30°
解简单的三角方程
例3.求适合下列各式的锐角α
解:
(1)
(2)
1、下列说法正确的是( )
A. tan80 °B. sin80 ° C. cos80 ° D. 以上都不对
新知练习
C
2、在△ABC中,∠C=90°,sinA= ,
则tanAcosA的值是( )
A. B.
C. D.
A
3、若 ,
则△ABC是( )
A.直角三角形
B.等边三角形
C.含有60°角的任意三角形
D.顶角为钝角的等腰三角形
A
4.计算:
(1)2sin30°- 3cos60 °
(2)cos 45°+tan60°·cos60°
(4)tan450·sin450-4sin300·cos450+cos2300
(3)
5、如图,在Rt△ABC中,∠C=90°,AC= ,BC= ,求∠A、∠B的度数。
A
C
B
我们学习了30°, 45°, 60°这几类特殊角的三角函数值.
α 30° 45° 60°
sinα
cosα
tanα
小结 :
锐角度数与三角函数值间的转化:
三角函数值
锐角度数
转化
小结 :
第3课时 特殊角的三角函数值
23.1锐角的三角函数
第23章 解直三角形
沪科版数学九年级上
复习:
1.锐角三角函数的定义
在 中,
∠A的余弦 :
∠A的正弦:
b
A
B
C
a
┌
c
当∠A+∠B=90°时
公式二
2、三角公式
tanA . tanB=1
公式一
sinA=cosB cosA=sinB
Sin30°=
cos30°=
tan30°=
新知探究
已知Rt△ABC中,∠A=30°
Sin60°=
cos60°=
tan60°=
60°
已知Rt△ABC中,∠A=30°
cos45°=
tan45°=
Sin45°=
已知Rt△ABC中,∠A=45°
归纳
特殊角的三角函数值
30o 45o 60o
sinα
cosα
tanα
1
30o 45o 60o
sinα
cosα
tanα
1
角度逐渐增大
正弦值如何变化
正弦值也增大
讨论:
30o 45o 60o
sinα
cosα
tanα
1
角度逐渐增大
余弦值如何变化
余弦值逐渐减小
讨论:
30o 45o 60o
sinα
cosα
tanα
1
角度逐渐增大
正切值如何变化
正切值也增大
讨论:
30o 45o 60o
sinα
cosα
tanα
1
讨论:
锐角A的正弦值、余弦值有无变化范围?
0< sinA<1
0
(1)当 时,α的正弦值随着角度的增大而增大。
(3)当 时,α的正切值随着角度的增大而增大。
(2)当 时, α的余弦值随着角度的增大而减小。
归纳
例1、求下列各式的值:
利用特殊的三角函数值进行计算
新知应用
例2 如图,在Rt△ABC中,∠C=90°,AC= ,BC= ,求∠A的度数。
A
C
B
解:在Rt△ABC
∵tanA=
∴∠A=30°
解简单的三角方程
例3.求适合下列各式的锐角α
解:
(1)
(2)
1、下列说法正确的是( )
A. tan80 °
新知练习
C
2、在△ABC中,∠C=90°,sinA= ,
则tanAcosA的值是( )
A. B.
C. D.
A
3、若 ,
则△ABC是( )
A.直角三角形
B.等边三角形
C.含有60°角的任意三角形
D.顶角为钝角的等腰三角形
A
4.计算:
(1)2sin30°- 3cos60 °
(2)cos 45°+tan60°·cos60°
(4)tan450·sin450-4sin300·cos450+cos2300
(3)
5、如图,在Rt△ABC中,∠C=90°,AC= ,BC= ,求∠A、∠B的度数。
A
C
B
我们学习了30°, 45°, 60°这几类特殊角的三角函数值.
α 30° 45° 60°
sinα
cosα
tanα
小结 :
锐角度数与三角函数值间的转化:
三角函数值
锐角度数
转化
小结 :
