2.2向心力与向心加速度 课时检测(Word版含答案)
文档属性
| 名称 | 2.2向心力与向心加速度 课时检测(Word版含答案) |  | |
| 格式 | doc | ||
| 文件大小 | 473.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 粤教版(2019) | ||
| 科目 | 物理 | ||
| 更新时间 | 2021-12-26 10:34:34 | ||
图片预览




文档简介
2.2向心力与向心加速度 课时检测(解析版)
一、选择题
1.下列说法正确的是( )
A.在推导匀变速直线运动位移公式时,把整个运动过程划分成很多小段,每一小段近似看做匀速直线运动,然后把各小段的位移相加,这里采用了微元法
B.做圆周运动的物体其向心加速度可以不指向圆心
C.在不需要考虑物体本身的大小和形状,用质点来代替物体的方法叫等效替代法
D.用比值法定义的物理量在物理学中占有相当大的比例,例如加速度就是采用比值法定义的
2.如图所示,AB为竖直转轴,细绳AC和BC的结点C系一质量为m的小球,两绳能承受的最大拉力均为。当AC和BC拉直时,,,。细绳AC和BC能绕竖直轴AB匀速转动,因而小球在水平面内做匀速圆周运动。当小球的线速度增大时,则最先被拉断的那根绳及此时小球的速度大小分别为(重力加速度)( )
A.AC B.BC
C.AC D.BC
3.两轮用齿轮传动,且不打滑,图中两轮的边缘上有A、B两点,它们到各自转轴O1、O2的距离分别为rA、rB,且rA>rB当轮子转动时,这两点的线速度大小分别为vA和vB,向心加速度大小分别为aA和aB,角速度大小分别为ωA和ωB,周期分别为TA和TB,则下列关系式正确的是( )
A.vA>vB B.ωA>ωB C.aA> aB D.TA>TB
4.一物体在某一匀速圆周运动中,下列物理量恒定不变的是( )
A.线速度 B.转速 C.向心力 D.向心加速度
5.如图所示,当用板手拧螺母时,扳手上的P、Q两点的角速度分别为和,加速度 大小分别为和,则( )
A.< ,< B.< ,=
C.=,< D.=,>
6.下列关于曲线运动的说法正确的是( )
A.做曲线运动的物体速度可能是不变的
B.做圆周运动的物体所受合力的方向一定指向圆心
C.曲线运动的加速度方向与速度方向可能在同一直线上
D.两个互成角度初速度不为零的匀变速直线运动的合运动可能是曲线运动
7.如图所示,A、B是两个摩擦传动轮,两轮半径大小关系为RA=2RB,则两轮边缘上的( )
A.角速度之比ωA∶ωB=2∶1
B.周期之比TA∶TB=1∶2
C.转速之比nA∶nB=1∶2
D.向心加速度之比aA∶aB=2∶1
8.将地球视为均匀的球体,设地球赤道上相对地面静止的物体,其随地球自转做匀速圆周运动的线速度为v,地球的半径为R。则地球表面上北纬60°处随地球自转的物体的向心加速度大小为( )
A. B. C. D.
9.如图,篮球正绕指尖所在竖直轴旋转,则篮球表面不在轴线上的各点( )
A.角速度相等 B.线速度相等
C.加速度相等 D.周期不相等
10.如图所示,长度为的轻质细杆OA,A端有一质量为的小球,以O点为圆心,在竖直平面内做圆周运动,小球通过最高点时的速度为,取,则此时轻杆OA将( )
A.受到的拉力 B.受到的压力
C.受到的拉力 D.受到的压力
11.如图所示,小明同学正在荡秋千,关于绳上a点和b点的各物理量,下列关系正确的是( )
A.
B.
C.
D.
12.做匀速圆周运动的两物体甲和乙质量相等,它们的向心加速度分别为和,轨道半径分别为和,且、,下列判断正确的是( )
A.甲的线速度大于乙的线速度 B.甲的角速度大于乙的角速度
C.甲的周期小于乙的周期 D.甲的向心力小于乙的向心力
13.对于做匀速圆周运动的物体,下面说法中正确的是( )
A.向心力不变 B.线速度不变 C.角速度不变 D.周期不变
14.下列各种运动中,属于匀变速运动的有( )
A.匀速直线运动 B.匀速圆周运动
C.平抛运动 D.自由落体运动
15.游乐场中的摩天轮,其运动可视为匀速圆周运动。关于匀速圆周运动的物体,下列说法错误的是( )
A.物体的匀速圆周运动是变速运动
B.物体在任意相等时间内通过的位移相等
C.物体所受的合力始终指向圆心
D.物体所受的合力只改变速度的大小,不改变速度的方向
二、解答题
16.如图,水平转盘上放有质量为 m 的物块,当物块到转轴的距离为 r 时,连接物块和转轴的绳刚好被拉直(绳上张力为零)。物体和转盘间最大静摩擦力是其正压力的μ倍。重力加速度为g,求:
(1)当转盘角速度ω1=时,细绳的拉力F1
(2)当转盘角速度ω2=时,细绳的拉力F2
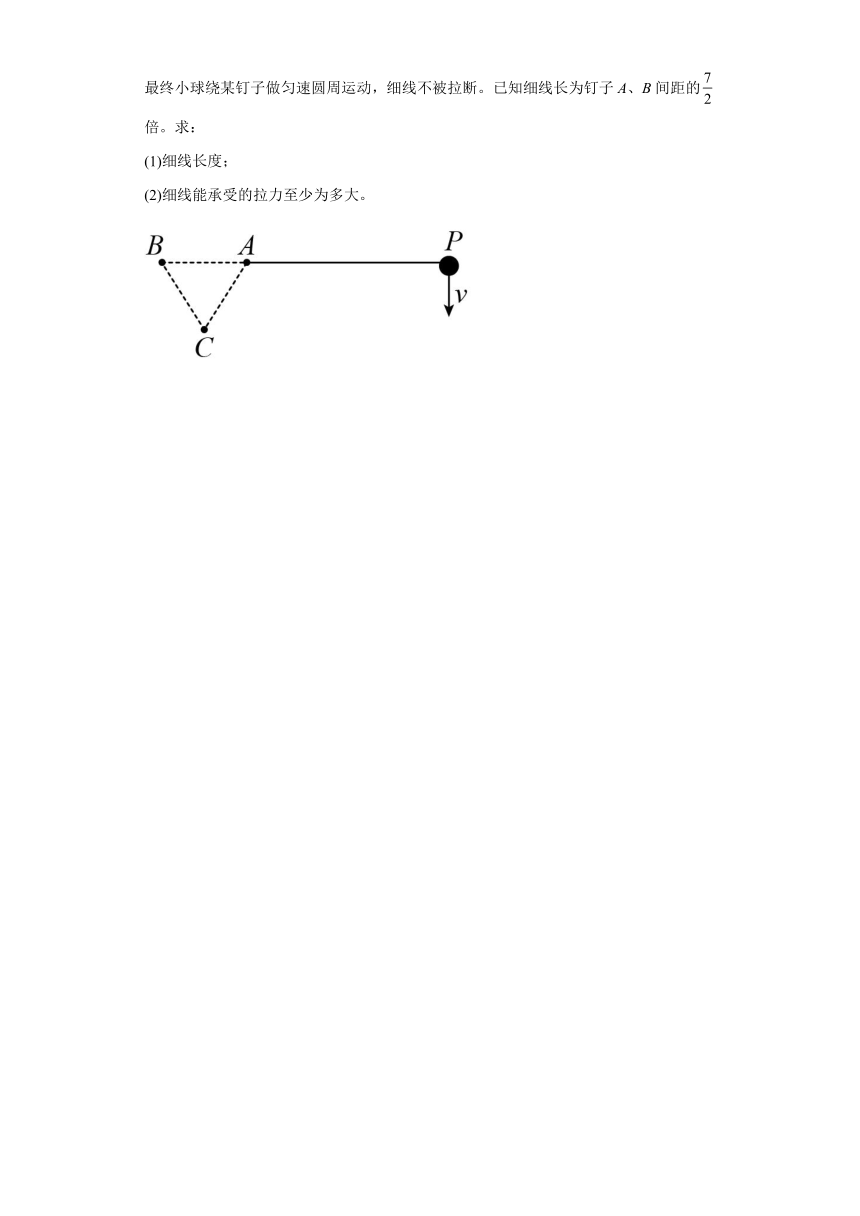
17.如图所示,在光滑的水平面上竖直固定着三个光滑钉子A、B和C(可视为质点),A、B、C位于等边三角形的三个顶点上。不可伸长的轻质细线一端定在A上,另一端拴一个质量为m的小球P。当P和AB在一条直线上时,给小球一垂直AB方向速度v使其绕A顺时针运动,经过时间t0细线接触钉子C。之后小球绕C点做圆周运动……最终小球绕某钉子做匀速圆周运动,细线不被拉断。已知细线长为钉子A、B间距的倍。求:
(1)细线长度;
(2)细线能承受的拉力至少为多大。
参考答案
1.A
【详解】
A.在推导匀变速直线运动位移公式时,把整个运动过程划分成很多小段,每一小段近似看做匀速直线运动,然后把各小段的位移相加,这里采用了微元法,选项A正确;
B.做圆周运动的物体其向心加速度总是指向圆心,选项B错误;
C.在不需要考虑物体本身的大小和形状,用质点来代替物体的方法叫理想模型法,选项C错误;
D.加速度
即加速度与外力和质量都有关,不是采用比值法定义的,选项D错误。
故选A。
2.B
【详解】
对小球C分析可知竖直方向
解得
TAC为定值且小于最大拉力,则AC不可能被拉断;当BC被拉断时
解得
故选B。
3.D
【详解】
A.轮子边缘上的点,靠齿轮传动,两点的线速度相等
故A错误;
B.A、B两点的线速度相等,由于.根据
可知
故B错误;
C.由
得,r越大,a越小,所以
故C错误;
D.根据
可知角速度越大则周期越小,可知A点的周期大,即
故D正确。
故选D。
4.B
【详解】
在描述匀速圆周运动的物理量中,线速度、向心加速度、向心力这几个物理量都是矢量,虽然其大小不变但是方向在变,因此这些物理量是变化的,周期、转速是标量,是不变化的,故B正确,ACD错误。
故选B。
5.C
【详解】
由于P、Q两点属于同轴转动,所以P、Q两点的角速度是相等的,由图可知Q点到螺母的距离较大,由
可知,Q点的加速度较大。
故选C。
6.D
【详解】
A.做曲线运动的物体速度方向一定是变化的,则速度一定变化,选项A错误;
B.只有做匀速圆周运动的物体所受合力的方向才一定指向圆心,选项B错误;
C.曲线运动的加速度方向与速度方向不可能在同一直线上,选项C错误;
D.两个互成角度初速度不为零的匀变速直线运动的合运动,如果合初速度和合加速度不共线,则合运动是曲线运动,选项D正确。
故选D。
7.C
【详解】
AC.两轮通过摩擦传动,边缘线速度相等,由
可得,角速度与半径成反比,即角速度之比
ωA∶ωB=1∶2
转速为
可知,转速之比为
nA∶nB=1∶2
A错误,C正确;
B.周期为
可得周期之比为
TA∶TB=2∶1
B错误;
D.向心加速度为
可得向心加速度之比为
aA∶aB=1∶2
D错误。
故选C。
8.C
【详解】
地球的自转角速度为
地球表面上北纬60°处随地球自转的物体的向心加速度大小为
C正确。
故选C。
9.A
【详解】
AD.篮球绕指尖所在竖直轴旋转,则篮球表面不在轴线上的各点属于同轴转动,角速度相同,周期相同,选项A正确,D错误;
B.篮球表面不在轴线上的各点半径不同,根据可知各点线速度不相等,选项B错误;
C.篮球表面不在轴线上的各点半径不同,根据可知各点加速度不相等,选项C错误。
故选A。
10.A
【详解】
假设杆对小球拉力大小为T,根据牛顿第二定律
解得
由于算出的拉力为正值,假设成立。
故选A。
11.C
【详解】
荡秋千可看作为同轴转动,所以a点和b点角速度相等,并且据图可看出
根据
可知
再根据
可知
故选C。
12.A
【详解】
A.根据向心加速度与线速度的关系有
a =
整理有
v甲 = ,v乙 =
由于
,
则甲的线速度大于乙的线速度,A正确;
B.根据向心加速度与角速度的关系有
a = rω2
整理有
ω甲 = ,ω乙 =
由于甲、乙两物体的向心加速度、做圆周运动的半径不明确,则无法判断它们角速度的大小关系,B错误;
C.由选项B可知,甲、乙两物体的角速度的大小关系,从而也无法判断出它们的周期关系,C错误;
D.根据向心力与向心加速度的关系有
F向甲 = ma1,F向乙 = ma2
则甲的向心力大于乙的向心力,D错误。
故选A。
13.CD
【详解】
做匀速圆周运动的物体,在相等的时间内转的弧长相等,所以物体所受的合外力大小、运动的线速度大小、角速度、周期都不变,可所受的合外力、运动的线速度都是矢量,大小虽不变,可方向时刻在变化,AB错误,CD正确。
故选CD。
14.CD
【详解】
A.匀速直线运动没有加速度,不是匀变速运动, A错误;
B.匀速圆周运动受到的合力提供向心力,产生向心加速度,但是向心加速度的方向是在时刻变化的,所以不是匀变速运动, B错误;
C.平抛运动是只在重力的作用下,加速度是重力加速度,是匀变速运动, C正确;
D.做自由落体运动的物体也是只受重力的作用,加速度是重力加速度,所以是匀变速运动, D正确。
故选CD。
15.BD
【详解】
A.物体的匀速圆周运动是速度大小不变,方向不断改变的变速运动,故A正确,不符合题意;
B.做匀速圆周运动的物体任意相等时间内通过的位移大小相等,方向不同,故B错误,符合题意;
C.做匀速圆周运动的物体所受的合力始终指向圆心,故C正确,不符合题意;
D.做匀速圆周运动的物体所受的合力只改变速度的方向,不改变速度的大小,故D错误,符合题意。
故选BD。
16.(1)0;(2)
【详解】
(1)当物块所需要的向心力等于最大静摩擦力时,转盘角速度最大 , 即
解得
由于 ,绳子为被拉紧,仅由摩擦力可提供向心力,则细绳对物块的拉力为零。
(2)由于 ,摩擦力不足以提供向心力,绳子也要提供部分向心力
解得
17.(1);(2)
【详解】
(1)开始阶段小球做匀速圆周运动的角速度设为ω0
根据
开始圆周运动的角速度
根据
v=ωR
可知细线长
解得
(2)设两钉子间距离为d,细线长度为L=3.5d
最终绕钉子A做圆周运动的半径R=0.5d,整个过程中最小半径为
根据向心力公式
可知,最终绕A点做圆周运动时需要的向心力最大,此时细线拉力设为Fm,根据向心力公式有
解得
一、选择题
1.下列说法正确的是( )
A.在推导匀变速直线运动位移公式时,把整个运动过程划分成很多小段,每一小段近似看做匀速直线运动,然后把各小段的位移相加,这里采用了微元法
B.做圆周运动的物体其向心加速度可以不指向圆心
C.在不需要考虑物体本身的大小和形状,用质点来代替物体的方法叫等效替代法
D.用比值法定义的物理量在物理学中占有相当大的比例,例如加速度就是采用比值法定义的
2.如图所示,AB为竖直转轴,细绳AC和BC的结点C系一质量为m的小球,两绳能承受的最大拉力均为。当AC和BC拉直时,,,。细绳AC和BC能绕竖直轴AB匀速转动,因而小球在水平面内做匀速圆周运动。当小球的线速度增大时,则最先被拉断的那根绳及此时小球的速度大小分别为(重力加速度)( )
A.AC B.BC
C.AC D.BC
3.两轮用齿轮传动,且不打滑,图中两轮的边缘上有A、B两点,它们到各自转轴O1、O2的距离分别为rA、rB,且rA>rB当轮子转动时,这两点的线速度大小分别为vA和vB,向心加速度大小分别为aA和aB,角速度大小分别为ωA和ωB,周期分别为TA和TB,则下列关系式正确的是( )
A.vA>vB B.ωA>ωB C.aA> aB D.TA>TB
4.一物体在某一匀速圆周运动中,下列物理量恒定不变的是( )
A.线速度 B.转速 C.向心力 D.向心加速度
5.如图所示,当用板手拧螺母时,扳手上的P、Q两点的角速度分别为和,加速度 大小分别为和,则( )
A.< ,< B.< ,=
C.=,< D.=,>
6.下列关于曲线运动的说法正确的是( )
A.做曲线运动的物体速度可能是不变的
B.做圆周运动的物体所受合力的方向一定指向圆心
C.曲线运动的加速度方向与速度方向可能在同一直线上
D.两个互成角度初速度不为零的匀变速直线运动的合运动可能是曲线运动
7.如图所示,A、B是两个摩擦传动轮,两轮半径大小关系为RA=2RB,则两轮边缘上的( )
A.角速度之比ωA∶ωB=2∶1
B.周期之比TA∶TB=1∶2
C.转速之比nA∶nB=1∶2
D.向心加速度之比aA∶aB=2∶1
8.将地球视为均匀的球体,设地球赤道上相对地面静止的物体,其随地球自转做匀速圆周运动的线速度为v,地球的半径为R。则地球表面上北纬60°处随地球自转的物体的向心加速度大小为( )
A. B. C. D.
9.如图,篮球正绕指尖所在竖直轴旋转,则篮球表面不在轴线上的各点( )
A.角速度相等 B.线速度相等
C.加速度相等 D.周期不相等
10.如图所示,长度为的轻质细杆OA,A端有一质量为的小球,以O点为圆心,在竖直平面内做圆周运动,小球通过最高点时的速度为,取,则此时轻杆OA将( )
A.受到的拉力 B.受到的压力
C.受到的拉力 D.受到的压力
11.如图所示,小明同学正在荡秋千,关于绳上a点和b点的各物理量,下列关系正确的是( )
A.
B.
C.
D.
12.做匀速圆周运动的两物体甲和乙质量相等,它们的向心加速度分别为和,轨道半径分别为和,且、,下列判断正确的是( )
A.甲的线速度大于乙的线速度 B.甲的角速度大于乙的角速度
C.甲的周期小于乙的周期 D.甲的向心力小于乙的向心力
13.对于做匀速圆周运动的物体,下面说法中正确的是( )
A.向心力不变 B.线速度不变 C.角速度不变 D.周期不变
14.下列各种运动中,属于匀变速运动的有( )
A.匀速直线运动 B.匀速圆周运动
C.平抛运动 D.自由落体运动
15.游乐场中的摩天轮,其运动可视为匀速圆周运动。关于匀速圆周运动的物体,下列说法错误的是( )
A.物体的匀速圆周运动是变速运动
B.物体在任意相等时间内通过的位移相等
C.物体所受的合力始终指向圆心
D.物体所受的合力只改变速度的大小,不改变速度的方向
二、解答题
16.如图,水平转盘上放有质量为 m 的物块,当物块到转轴的距离为 r 时,连接物块和转轴的绳刚好被拉直(绳上张力为零)。物体和转盘间最大静摩擦力是其正压力的μ倍。重力加速度为g,求:
(1)当转盘角速度ω1=时,细绳的拉力F1
(2)当转盘角速度ω2=时,细绳的拉力F2
17.如图所示,在光滑的水平面上竖直固定着三个光滑钉子A、B和C(可视为质点),A、B、C位于等边三角形的三个顶点上。不可伸长的轻质细线一端定在A上,另一端拴一个质量为m的小球P。当P和AB在一条直线上时,给小球一垂直AB方向速度v使其绕A顺时针运动,经过时间t0细线接触钉子C。之后小球绕C点做圆周运动……最终小球绕某钉子做匀速圆周运动,细线不被拉断。已知细线长为钉子A、B间距的倍。求:
(1)细线长度;
(2)细线能承受的拉力至少为多大。
参考答案
1.A
【详解】
A.在推导匀变速直线运动位移公式时,把整个运动过程划分成很多小段,每一小段近似看做匀速直线运动,然后把各小段的位移相加,这里采用了微元法,选项A正确;
B.做圆周运动的物体其向心加速度总是指向圆心,选项B错误;
C.在不需要考虑物体本身的大小和形状,用质点来代替物体的方法叫理想模型法,选项C错误;
D.加速度
即加速度与外力和质量都有关,不是采用比值法定义的,选项D错误。
故选A。
2.B
【详解】
对小球C分析可知竖直方向
解得
TAC为定值且小于最大拉力,则AC不可能被拉断;当BC被拉断时
解得
故选B。
3.D
【详解】
A.轮子边缘上的点,靠齿轮传动,两点的线速度相等
故A错误;
B.A、B两点的线速度相等,由于.根据
可知
故B错误;
C.由
得,r越大,a越小,所以
故C错误;
D.根据
可知角速度越大则周期越小,可知A点的周期大,即
故D正确。
故选D。
4.B
【详解】
在描述匀速圆周运动的物理量中,线速度、向心加速度、向心力这几个物理量都是矢量,虽然其大小不变但是方向在变,因此这些物理量是变化的,周期、转速是标量,是不变化的,故B正确,ACD错误。
故选B。
5.C
【详解】
由于P、Q两点属于同轴转动,所以P、Q两点的角速度是相等的,由图可知Q点到螺母的距离较大,由
可知,Q点的加速度较大。
故选C。
6.D
【详解】
A.做曲线运动的物体速度方向一定是变化的,则速度一定变化,选项A错误;
B.只有做匀速圆周运动的物体所受合力的方向才一定指向圆心,选项B错误;
C.曲线运动的加速度方向与速度方向不可能在同一直线上,选项C错误;
D.两个互成角度初速度不为零的匀变速直线运动的合运动,如果合初速度和合加速度不共线,则合运动是曲线运动,选项D正确。
故选D。
7.C
【详解】
AC.两轮通过摩擦传动,边缘线速度相等,由
可得,角速度与半径成反比,即角速度之比
ωA∶ωB=1∶2
转速为
可知,转速之比为
nA∶nB=1∶2
A错误,C正确;
B.周期为
可得周期之比为
TA∶TB=2∶1
B错误;
D.向心加速度为
可得向心加速度之比为
aA∶aB=1∶2
D错误。
故选C。
8.C
【详解】
地球的自转角速度为
地球表面上北纬60°处随地球自转的物体的向心加速度大小为
C正确。
故选C。
9.A
【详解】
AD.篮球绕指尖所在竖直轴旋转,则篮球表面不在轴线上的各点属于同轴转动,角速度相同,周期相同,选项A正确,D错误;
B.篮球表面不在轴线上的各点半径不同,根据可知各点线速度不相等,选项B错误;
C.篮球表面不在轴线上的各点半径不同,根据可知各点加速度不相等,选项C错误。
故选A。
10.A
【详解】
假设杆对小球拉力大小为T,根据牛顿第二定律
解得
由于算出的拉力为正值,假设成立。
故选A。
11.C
【详解】
荡秋千可看作为同轴转动,所以a点和b点角速度相等,并且据图可看出
根据
可知
再根据
可知
故选C。
12.A
【详解】
A.根据向心加速度与线速度的关系有
a =
整理有
v甲 = ,v乙 =
由于
,
则甲的线速度大于乙的线速度,A正确;
B.根据向心加速度与角速度的关系有
a = rω2
整理有
ω甲 = ,ω乙 =
由于甲、乙两物体的向心加速度、做圆周运动的半径不明确,则无法判断它们角速度的大小关系,B错误;
C.由选项B可知,甲、乙两物体的角速度的大小关系,从而也无法判断出它们的周期关系,C错误;
D.根据向心力与向心加速度的关系有
F向甲 = ma1,F向乙 = ma2
则甲的向心力大于乙的向心力,D错误。
故选A。
13.CD
【详解】
做匀速圆周运动的物体,在相等的时间内转的弧长相等,所以物体所受的合外力大小、运动的线速度大小、角速度、周期都不变,可所受的合外力、运动的线速度都是矢量,大小虽不变,可方向时刻在变化,AB错误,CD正确。
故选CD。
14.CD
【详解】
A.匀速直线运动没有加速度,不是匀变速运动, A错误;
B.匀速圆周运动受到的合力提供向心力,产生向心加速度,但是向心加速度的方向是在时刻变化的,所以不是匀变速运动, B错误;
C.平抛运动是只在重力的作用下,加速度是重力加速度,是匀变速运动, C正确;
D.做自由落体运动的物体也是只受重力的作用,加速度是重力加速度,所以是匀变速运动, D正确。
故选CD。
15.BD
【详解】
A.物体的匀速圆周运动是速度大小不变,方向不断改变的变速运动,故A正确,不符合题意;
B.做匀速圆周运动的物体任意相等时间内通过的位移大小相等,方向不同,故B错误,符合题意;
C.做匀速圆周运动的物体所受的合力始终指向圆心,故C正确,不符合题意;
D.做匀速圆周运动的物体所受的合力只改变速度的方向,不改变速度的大小,故D错误,符合题意。
故选BD。
16.(1)0;(2)
【详解】
(1)当物块所需要的向心力等于最大静摩擦力时,转盘角速度最大 , 即
解得
由于 ,绳子为被拉紧,仅由摩擦力可提供向心力,则细绳对物块的拉力为零。
(2)由于 ,摩擦力不足以提供向心力,绳子也要提供部分向心力
解得
17.(1);(2)
【详解】
(1)开始阶段小球做匀速圆周运动的角速度设为ω0
根据
开始圆周运动的角速度
根据
v=ωR
可知细线长
解得
(2)设两钉子间距离为d,细线长度为L=3.5d
最终绕钉子A做圆周运动的半径R=0.5d,整个过程中最小半径为
根据向心力公式
可知,最终绕A点做圆周运动时需要的向心力最大,此时细线拉力设为Fm,根据向心力公式有
解得
同课章节目录
- 第一章 抛体运动
- 第一节 曲线运动
- 第二节 运动的合成与分解
- 第三节 平抛运动
- 第四节 生活和生产中的抛体运动
- 第二章 圆周运动
- 第一节 匀速圆周运动
- 第二节 向心力与向心加速度
- 第三节 生活中的圆周运动
- 第四节 离心现象及其应用
- 第三章 万有引力定律
- 第一节 认识天体运动
- 第二节 认识万有引力定律
- 第三节 万有引力定律的应用
- 第四节 宇宙速度与航天
- 第四章 机械能及其守恒定律
- 第一节 功
- 第二节 功率
- 第三节 动能 动能定理
- 第四节 势能
- 第五节 机械能守恒定律
- 第六节 验证机械能守恒定律
- 第七节 生产和生活中的机械能守恒
- 第五章 牛顿力学的局限性与相对论初步
- 第一节 牛顿力学的成就与局限性
- 第二节 相对论时空观
- 第三节 宇宙起源和演化
