人教版数学九年级上册24.4.1弧长及扇形面积课件(共19张PPT)
文档属性
| 名称 | 人教版数学九年级上册24.4.1弧长及扇形面积课件(共19张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 1.9MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-12-27 16:11:41 | ||
图片预览



文档简介
(共19张PPT)
人教版数学九年级上册24.4
弧长与扇形面积
24.4.1弧长和扇形面积
学习目标
1 了解扇形的概念;
2 理解并掌握弧长和扇形面积的计算 公式;
3 会利用弧长和扇形面积公式熟练计算。
A
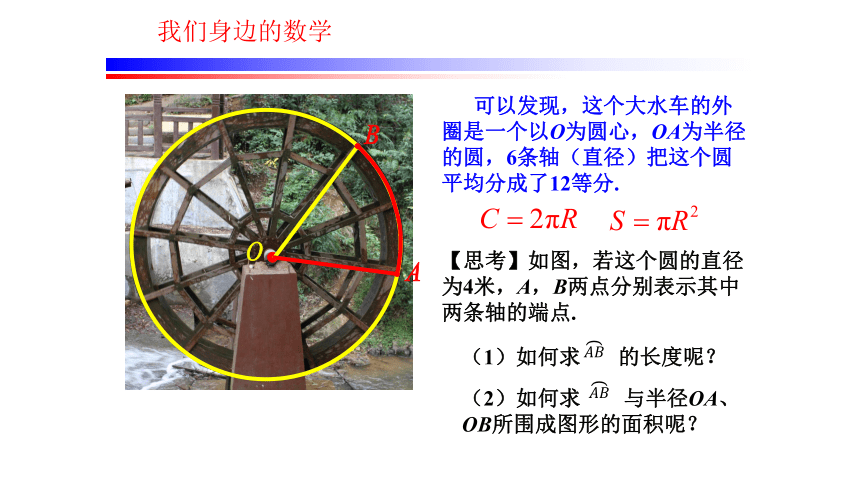
【思考】如图,若这个圆的直径为4米,A,B两点分别表示其中两条轴的端点.
可以发现,这个大水车的外圈是一个以O为圆心,OA为半径的圆,6条轴(直径)把这个圆平均分成了12等分.
O
B
(2)如何求 与半径OA、OB所围成图形的面积呢?
(1)如何求 的长度呢?
我们身边的数学
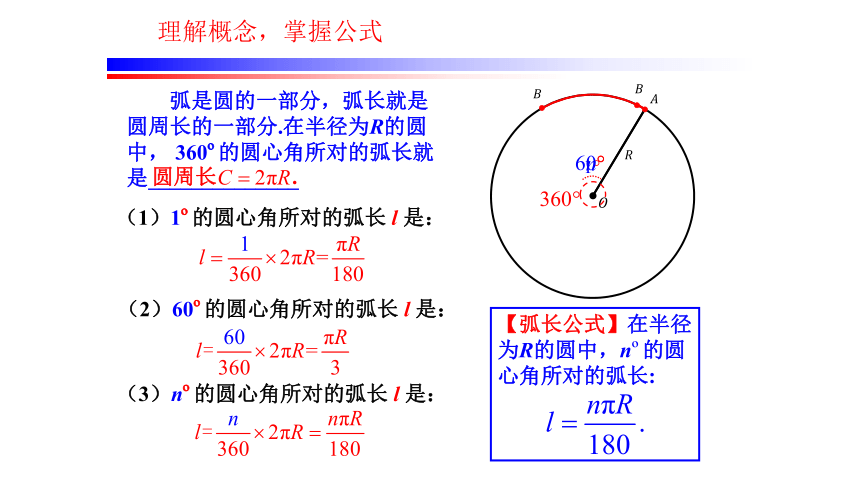
(1)1 的圆心角所对的弧长 l 是:
(3)n 的圆心角所对的弧长 l 是:
弧是圆的一部分,弧长就是圆周长的一部分.在半径为R的圆中, 360 的圆心角所对的弧长就是______________
(2)60 的圆心角所对的弧长 l 是:
【弧长公式】在半径为R的圆中,n 的圆心角所对的弧长:
圆周长 .
理解概念,掌握公式
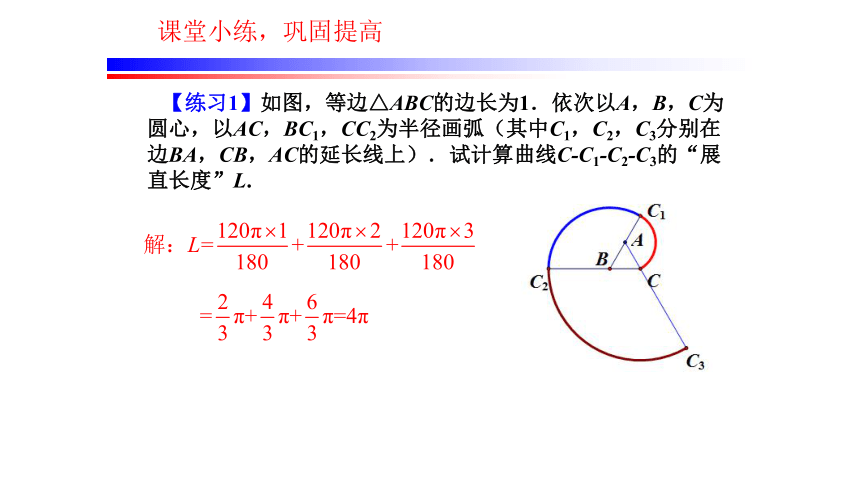
【练习1】如图,等边△ABC的边长为1.依次以A,B,C为圆心,以AC,BC1,CC2为半径画弧(其中C1,C2,C3分别在边BA,CB,AC的延长线上).试计算曲线C-C1-C2-C3的“展直长度”L.
课堂小练,巩固提高
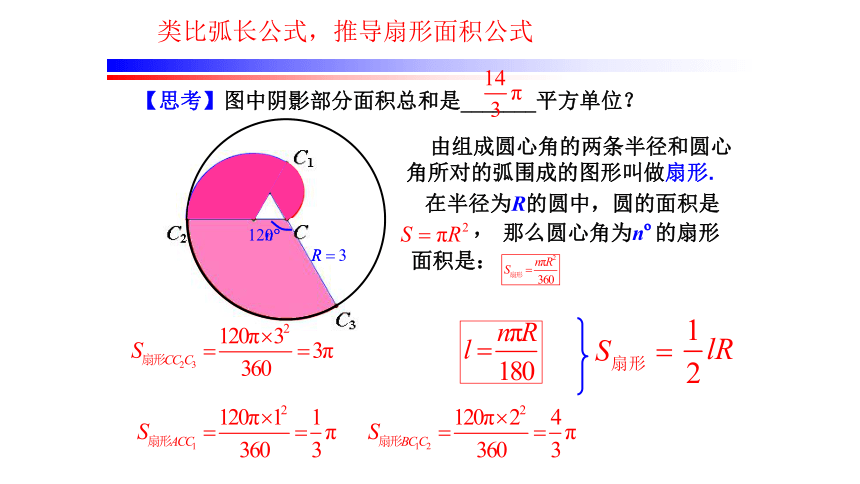
【思考】图中阴影部分面积总和是_______平方单位?
由组成圆心角的两条半径和圆心角所对的弧围成的图形叫做扇形.
在半径为R的圆中,圆的面积是
,
那么圆心角为n 的扇形
面积是:
类比弧长公式,推导扇形面积公式
如图,水平放置的圆柱形排水管道的截面半径是0.6 m,其中水面高0.3 m.求截面上有水部分的面积(结果保留小数点后两位).
由弦及其所对的弧组成的图形叫做弓形.
细心观察,认真思考
【变式】水平放置的圆柱形排水管道的截面半径是0.6 m,其中水面宽 m.那么截面上有水部分的面积为____________m2 (结果保留小数点后两位).
如图,水平放置的圆柱形排水管道的截面半径是0.6 m,其中水面高0.3 m.求截面上有水部分的面积(结果保留小数点后两位).
细心观察,认真思考
割补法
【练习2】如图,正三角形ABC的边长为a,D,E,F分别为BC,CA,AB的中点,以A,B,C三点为圆心, 长为半径作圆.求图中阴影部分的面积.
换成字母也一样
A
【思考】如图,若这个圆的直径为4米,A,B两点分别表示其中两条轴的端点.
可以发现,这个大水车的外圈是一个以O为圆心,OA为半径的圆,6条轴(直径)把这个圆平均分成了12等分.
O
B
(2)如何求 与半径OA、OB所围成图形的面积呢?
(1)如何求 的长度呢?
回归课题,解决问题
【数学日记】学习是一个知识积累的过程,在这个过程中,我们应当注意前后知识的联系、转化与类比等,这样,认识才能不断深化,能力才能不断提高.
回顾本节课知识,思考并回答下列问题:
(1)弧长和扇形面积公式是什么?
(2)你是如何推导得到这两个公式的?
通过知识之间的转化、类比来获得新知识.
(3)通常可以采用什么方法求不规则图形的面积?
割补法
善于总结是一个良好的学习习惯
课堂练习
1.75°的圆心角所对的弧长是2.5πcm,
则此弧所在圆的半径是 cm。
6
2.半径为6的圆中,30°圆周角所对的
弧长是 cm。
2π
4.一个扇形的弧长为20πcm,面积是
240πcm2 ,则扇形的半径 。
3. 一个扇形的圆心角为120°,它的面积为3πcm2,那么该扇形的半径 .
3cm
圆心角
24cm
150°
课堂练习
5、已知扇形的圆心角为120°,半径为2,
则这个扇形的面积,S扇= _ .
6、已知半径为2的扇形,其弧长为 ,
则这个扇形的面积,S扇= ——.
如图,继续依次以A,B,C……为圆心,AC3 , BC4 ,CC5 ……为半径画弧……,试探究曲线C-C1-C2…-Cn的“展直长度”为:_________(用含n的代数式表示).
课后探究,提升思维
运用新知 提升能力
A
B
C
A'
C'
B'
A"
L
1.把Rt△ABC的斜边放在直线L上,绕点B按顺时
针方向在L上转两次,使它转到A"B'C',设BC=1,
∠CAB=30° ,则顶点A运动到点A"的位置时,
(1)点A所经过的路线长是多少?
运用新知 提升能力
1.把Rt△ABC的斜边放在直线L上,绕点B按顺时
针方向在L上转两次,使它转到A"B'C',设BC=1,
∠CAB=30° ,则顶点A运动到点A"的位置时,
(1)点A所经过的路线长是多少?
(2)点A所经过的路线长与L所围成的面积?
A
B
C
A'
C'
B'
A"
L
2.如图,已知菱形ABCD的边长为1.5,B,C两点在扇形AEF的弧EF上,
求: 及扇形ABC的面积.
⌒
BC
运用新知 提升能力
祝:同学们学习进步 !
同仁们工作顺利 !
人教版数学九年级上册24.4
弧长与扇形面积
24.4.1弧长和扇形面积
学习目标
1 了解扇形的概念;
2 理解并掌握弧长和扇形面积的计算 公式;
3 会利用弧长和扇形面积公式熟练计算。
A
【思考】如图,若这个圆的直径为4米,A,B两点分别表示其中两条轴的端点.
可以发现,这个大水车的外圈是一个以O为圆心,OA为半径的圆,6条轴(直径)把这个圆平均分成了12等分.
O
B
(2)如何求 与半径OA、OB所围成图形的面积呢?
(1)如何求 的长度呢?
我们身边的数学
(1)1 的圆心角所对的弧长 l 是:
(3)n 的圆心角所对的弧长 l 是:
弧是圆的一部分,弧长就是圆周长的一部分.在半径为R的圆中, 360 的圆心角所对的弧长就是______________
(2)60 的圆心角所对的弧长 l 是:
【弧长公式】在半径为R的圆中,n 的圆心角所对的弧长:
圆周长 .
理解概念,掌握公式
【练习1】如图,等边△ABC的边长为1.依次以A,B,C为圆心,以AC,BC1,CC2为半径画弧(其中C1,C2,C3分别在边BA,CB,AC的延长线上).试计算曲线C-C1-C2-C3的“展直长度”L.
课堂小练,巩固提高
【思考】图中阴影部分面积总和是_______平方单位?
由组成圆心角的两条半径和圆心角所对的弧围成的图形叫做扇形.
在半径为R的圆中,圆的面积是
,
那么圆心角为n 的扇形
面积是:
类比弧长公式,推导扇形面积公式
如图,水平放置的圆柱形排水管道的截面半径是0.6 m,其中水面高0.3 m.求截面上有水部分的面积(结果保留小数点后两位).
由弦及其所对的弧组成的图形叫做弓形.
细心观察,认真思考
【变式】水平放置的圆柱形排水管道的截面半径是0.6 m,其中水面宽 m.那么截面上有水部分的面积为____________m2 (结果保留小数点后两位).
如图,水平放置的圆柱形排水管道的截面半径是0.6 m,其中水面高0.3 m.求截面上有水部分的面积(结果保留小数点后两位).
细心观察,认真思考
割补法
【练习2】如图,正三角形ABC的边长为a,D,E,F分别为BC,CA,AB的中点,以A,B,C三点为圆心, 长为半径作圆.求图中阴影部分的面积.
换成字母也一样
A
【思考】如图,若这个圆的直径为4米,A,B两点分别表示其中两条轴的端点.
可以发现,这个大水车的外圈是一个以O为圆心,OA为半径的圆,6条轴(直径)把这个圆平均分成了12等分.
O
B
(2)如何求 与半径OA、OB所围成图形的面积呢?
(1)如何求 的长度呢?
回归课题,解决问题
【数学日记】学习是一个知识积累的过程,在这个过程中,我们应当注意前后知识的联系、转化与类比等,这样,认识才能不断深化,能力才能不断提高.
回顾本节课知识,思考并回答下列问题:
(1)弧长和扇形面积公式是什么?
(2)你是如何推导得到这两个公式的?
通过知识之间的转化、类比来获得新知识.
(3)通常可以采用什么方法求不规则图形的面积?
割补法
善于总结是一个良好的学习习惯
课堂练习
1.75°的圆心角所对的弧长是2.5πcm,
则此弧所在圆的半径是 cm。
6
2.半径为6的圆中,30°圆周角所对的
弧长是 cm。
2π
4.一个扇形的弧长为20πcm,面积是
240πcm2 ,则扇形的半径 。
3. 一个扇形的圆心角为120°,它的面积为3πcm2,那么该扇形的半径 .
3cm
圆心角
24cm
150°
课堂练习
5、已知扇形的圆心角为120°,半径为2,
则这个扇形的面积,S扇= _ .
6、已知半径为2的扇形,其弧长为 ,
则这个扇形的面积,S扇= ——.
如图,继续依次以A,B,C……为圆心,AC3 , BC4 ,CC5 ……为半径画弧……,试探究曲线C-C1-C2…-Cn的“展直长度”为:_________(用含n的代数式表示).
课后探究,提升思维
运用新知 提升能力
A
B
C
A'
C'
B'
A"
L
1.把Rt△ABC的斜边放在直线L上,绕点B按顺时
针方向在L上转两次,使它转到A"B'C',设BC=1,
∠CAB=30° ,则顶点A运动到点A"的位置时,
(1)点A所经过的路线长是多少?
运用新知 提升能力
1.把Rt△ABC的斜边放在直线L上,绕点B按顺时
针方向在L上转两次,使它转到A"B'C',设BC=1,
∠CAB=30° ,则顶点A运动到点A"的位置时,
(1)点A所经过的路线长是多少?
(2)点A所经过的路线长与L所围成的面积?
A
B
C
A'
C'
B'
A"
L
2.如图,已知菱形ABCD的边长为1.5,B,C两点在扇形AEF的弧EF上,
求: 及扇形ABC的面积.
⌒
BC
运用新知 提升能力
祝:同学们学习进步 !
同仁们工作顺利 !
同课章节目录
