2021-2022学年人教版数学九年级上册24.4弧长及扇形面积课件(共24张PPT)
文档属性
| 名称 | 2021-2022学年人教版数学九年级上册24.4弧长及扇形面积课件(共24张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 976.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-12-27 16:14:51 | ||
图片预览





文档简介
(共24张PPT)
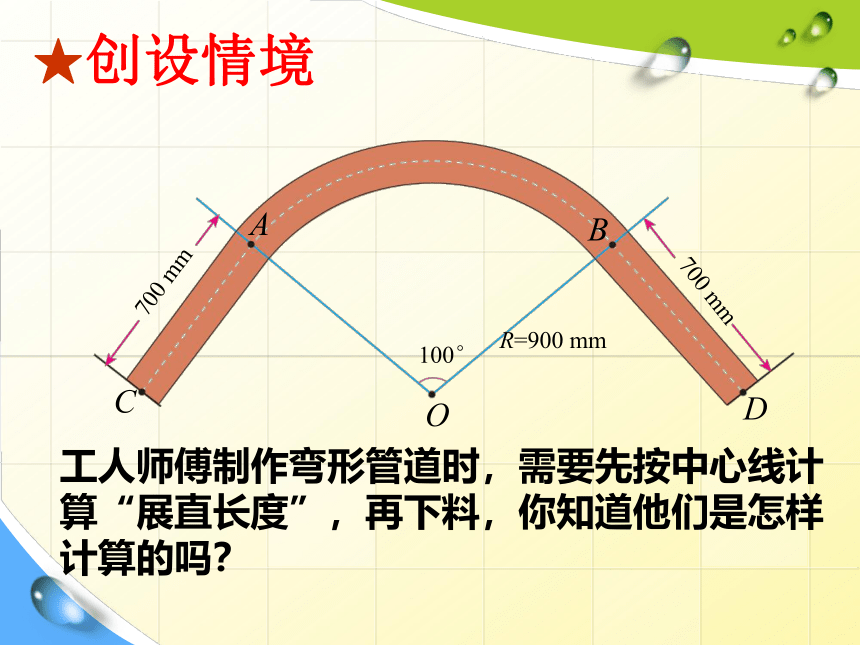
★创设情境
工人师傅制作弯形管道时,需要先按中心线计算“展直长度”,再下料,你知道他们是怎样计算的吗?
A
B
C
D
O
R=900 mm
700 mm
700 mm
100°
★学习目标
1.以圆的周长和面积为基础,探究弧长和扇形的面积公式,并会用于计算弧长和扇形面积.
2.能利用弧长、扇形面积计算公式计算简单组合图形的周长和面积.
3.在弧长和扇形面积公式的推导过程中,发现弧长与圆周长、扇形面积与圆面积都是部分与整体之间的关系,从而将计算弧长和扇形面积的问题转化为求圆周长和圆面积的一部分来解决,体会转化、类比的数学思想.
★合作探究 达成目标
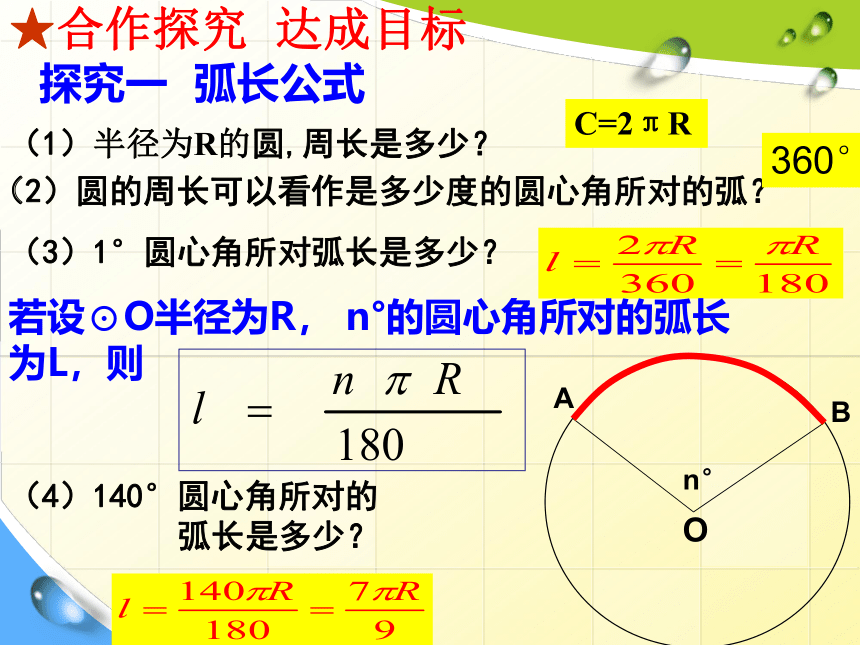
探究一 弧长公式
(1)半径为R的圆,周长是多少?
C=2πR
(2)圆的周长可以看作是多少度的圆心角所对的弧?
360°
(3)1°圆心角所对弧长是多少?
若设⊙O半径为R, n°的圆心角所对的弧长
为L,则
n°
A
B
O
(4)140°圆心角所对的
弧长是多少?
弧长的大小由哪些量决定?
圆的大小(半径)、圆心角的度数.
★试一试 我能行
例1 已知圆弧的半径为50厘米,圆心角为60°,求此圆弧的长度。
解:
=
(cm)
答:此圆弧的长度为
cm
2. 有一段弯道是圆弧形的,道长是12 m,弧所对的圆心角是81°,这段圆弧所在圆的半径R是多少米(结果保留小数点后一位)?
★我会用
1. 弧长相等的两段弧是等弧吗?
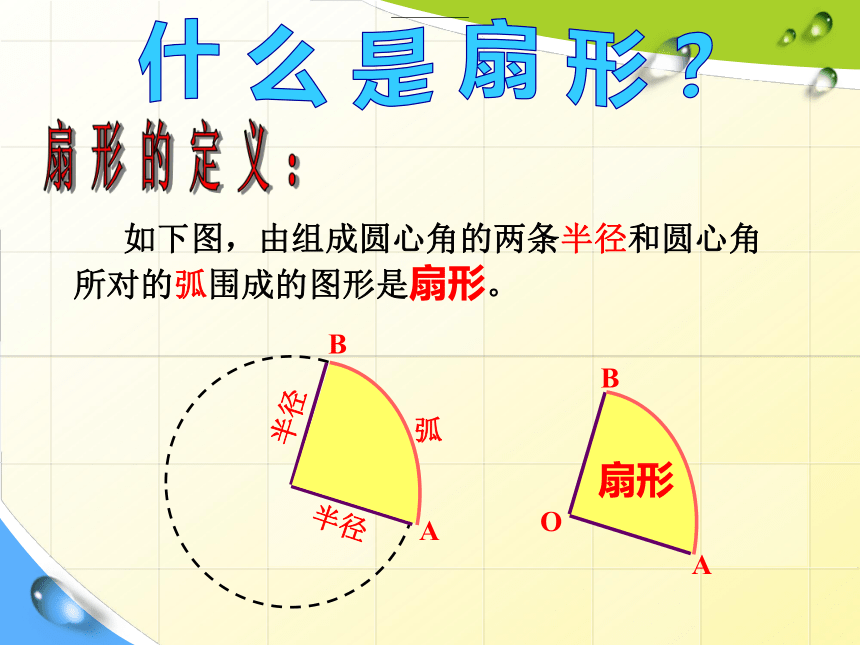
如下图,由组成圆心角的两条半径和圆心角所对的弧围成的图形是扇形。
半径
半径
弧
A
B
O
B
A
扇形
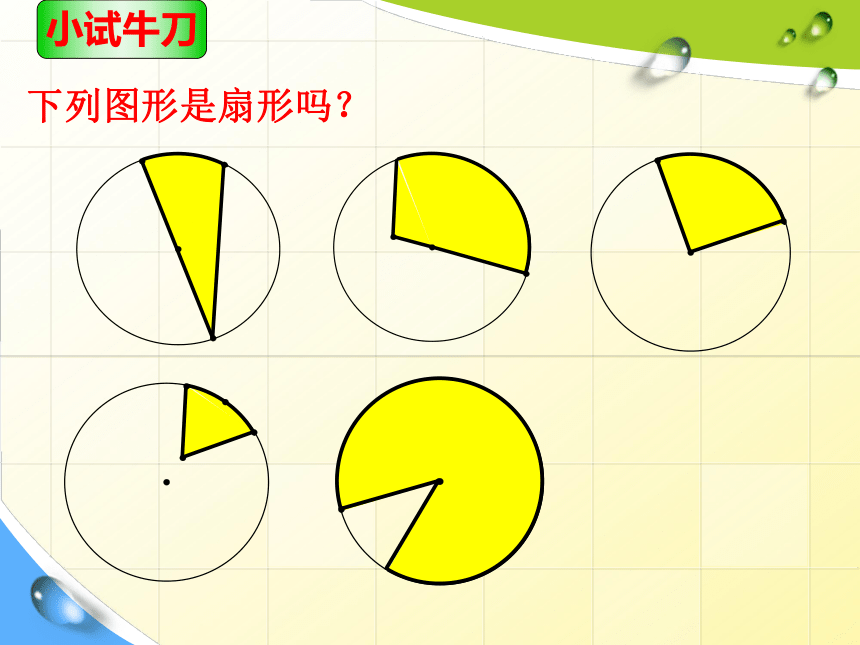
下列图形是扇形吗?
小试牛刀
探究二 扇形面积
那么: 在半径为R 的圆中,n°的圆心角所对的扇形面积的计算公式为
如果圆的半径为R,则圆的面积为 ,
l°的圆心角对应的扇形面积为 ,
n°的圆心角对应的扇形面积为
n°
l
O
想一想:扇形的面积公式与什么公式类似?
探索弧长与扇形面积的关系
R
S
比较扇形面积公式 和弧长公式 ,你能用弧长表示扇形面积吗?
S扇形
A
B
O
O
比较扇形面积与弧长公式, 用弧长表示扇形面积:
1、已知扇形的圆心角为120°,半径为2,则这个扇形的面积,S扇=____.
2、已知半径为2的扇形,面积 ,
则它的圆心角的度数为___.
120°
★我会用
例2:如图、水平放置的圆柱形排水管道的截面半径是0.6cm,其中水面高0.3cm,求截面上有水部分的面积。
0
B
A
C
有水部分的面积 = S扇- S△
D
★试一试 我能行
如图、水平放置的圆柱形排水管道的截面半径是0.6cm,其中水面高0.9cm,求截面上有水部分的面积。(结果保留 )
0
A
B
D
C
E
有水部分的面积
= S扇+ S△
★摇身变一变
★我会用
2.已知扇形的圆心角为1500,弧长为 ,则扇形的面积为__________.
1.已知扇形的圆心角为300,面积为 ,则这个扇形的半径R=____.
6cm
1.在半径为1的⊙O中,120°的圆心角所对的弧长是________.
2.如图,两个同心圆中,大圆的半径为2,∠AOB=120°,半径OE平分∠AOB,则图中阴影部分的面积为__________.
★课堂练习
B
B
3.如图,已知扇形的圆心角为60°,半径为 ,则图中弓形的面积为( )
A. B. C. D.
C
★课堂练习
4、如图,这是中央电视台“曲苑杂谈”中的一副图案,它是一扇形图形,其中∠AOB为120°,OC长为8cm,CA长为12cm,则贴纸部分的面
积为( )
A. B.
C. D.
★课堂练习
5、已知扇形面积为 ,圆心角为60°,
则这个扇形的半径R=____.
6、如图,方格纸中4个小正方形的边长均为1,
则图中阴影部分三个小扇形的面积和为
(结果保留
).
★课堂练习
A.
B.
C.
D.
7.如图,等边△ABC
的边长为12cm,
切
边BC于D点,
则图中阴影部分的
内切⊙O
面积为( )
C
★课堂练习
O
8.如图,正六边形内接于圆O,
圆O的半径为10,
则圆中阴影部分的面积为_____.
★课堂练习
1.弧长公式:
2.由组成圆心角的两条半径和圆心角所对的
弧围成的图形叫做( )
3.扇形的面积公式:
扇形
S扇形= =
★创设情境
工人师傅制作弯形管道时,需要先按中心线计算“展直长度”,再下料,你知道他们是怎样计算的吗?
A
B
C
D
O
R=900 mm
700 mm
700 mm
100°
★学习目标
1.以圆的周长和面积为基础,探究弧长和扇形的面积公式,并会用于计算弧长和扇形面积.
2.能利用弧长、扇形面积计算公式计算简单组合图形的周长和面积.
3.在弧长和扇形面积公式的推导过程中,发现弧长与圆周长、扇形面积与圆面积都是部分与整体之间的关系,从而将计算弧长和扇形面积的问题转化为求圆周长和圆面积的一部分来解决,体会转化、类比的数学思想.
★合作探究 达成目标
探究一 弧长公式
(1)半径为R的圆,周长是多少?
C=2πR
(2)圆的周长可以看作是多少度的圆心角所对的弧?
360°
(3)1°圆心角所对弧长是多少?
若设⊙O半径为R, n°的圆心角所对的弧长
为L,则
n°
A
B
O
(4)140°圆心角所对的
弧长是多少?
弧长的大小由哪些量决定?
圆的大小(半径)、圆心角的度数.
★试一试 我能行
例1 已知圆弧的半径为50厘米,圆心角为60°,求此圆弧的长度。
解:
=
(cm)
答:此圆弧的长度为
cm
2. 有一段弯道是圆弧形的,道长是12 m,弧所对的圆心角是81°,这段圆弧所在圆的半径R是多少米(结果保留小数点后一位)?
★我会用
1. 弧长相等的两段弧是等弧吗?
如下图,由组成圆心角的两条半径和圆心角所对的弧围成的图形是扇形。
半径
半径
弧
A
B
O
B
A
扇形
下列图形是扇形吗?
小试牛刀
探究二 扇形面积
那么: 在半径为R 的圆中,n°的圆心角所对的扇形面积的计算公式为
如果圆的半径为R,则圆的面积为 ,
l°的圆心角对应的扇形面积为 ,
n°的圆心角对应的扇形面积为
n°
l
O
想一想:扇形的面积公式与什么公式类似?
探索弧长与扇形面积的关系
R
S
比较扇形面积公式 和弧长公式 ,你能用弧长表示扇形面积吗?
S扇形
A
B
O
O
比较扇形面积与弧长公式, 用弧长表示扇形面积:
1、已知扇形的圆心角为120°,半径为2,则这个扇形的面积,S扇=____.
2、已知半径为2的扇形,面积 ,
则它的圆心角的度数为___.
120°
★我会用
例2:如图、水平放置的圆柱形排水管道的截面半径是0.6cm,其中水面高0.3cm,求截面上有水部分的面积。
0
B
A
C
有水部分的面积 = S扇- S△
D
★试一试 我能行
如图、水平放置的圆柱形排水管道的截面半径是0.6cm,其中水面高0.9cm,求截面上有水部分的面积。(结果保留 )
0
A
B
D
C
E
有水部分的面积
= S扇+ S△
★摇身变一变
★我会用
2.已知扇形的圆心角为1500,弧长为 ,则扇形的面积为__________.
1.已知扇形的圆心角为300,面积为 ,则这个扇形的半径R=____.
6cm
1.在半径为1的⊙O中,120°的圆心角所对的弧长是________.
2.如图,两个同心圆中,大圆的半径为2,∠AOB=120°,半径OE平分∠AOB,则图中阴影部分的面积为__________.
★课堂练习
B
B
3.如图,已知扇形的圆心角为60°,半径为 ,则图中弓形的面积为( )
A. B. C. D.
C
★课堂练习
4、如图,这是中央电视台“曲苑杂谈”中的一副图案,它是一扇形图形,其中∠AOB为120°,OC长为8cm,CA长为12cm,则贴纸部分的面
积为( )
A. B.
C. D.
★课堂练习
5、已知扇形面积为 ,圆心角为60°,
则这个扇形的半径R=____.
6、如图,方格纸中4个小正方形的边长均为1,
则图中阴影部分三个小扇形的面积和为
(结果保留
).
★课堂练习
A.
B.
C.
D.
7.如图,等边△ABC
的边长为12cm,
切
边BC于D点,
则图中阴影部分的
内切⊙O
面积为( )
C
★课堂练习
O
8.如图,正六边形内接于圆O,
圆O的半径为10,
则圆中阴影部分的面积为_____.
★课堂练习
1.弧长公式:
2.由组成圆心角的两条半径和圆心角所对的
弧围成的图形叫做( )
3.扇形的面积公式:
扇形
S扇形= =
同课章节目录
