2021-2022学年华东师大版八年级数学上册第14章勾股定理期末综合复习训练题(Word版,附答案解析)
文档属性
| 名称 | 2021-2022学年华东师大版八年级数学上册第14章勾股定理期末综合复习训练题(Word版,附答案解析) |

|
|
| 格式 | zip | ||
| 文件大小 | 179.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-12-27 00:00:00 | ||
图片预览



文档简介
2021-2022学年华师大版八年级数学上册
《第14章勾股定理》期末综合复习训练题
1.已知Rt△ABC中,∠A,∠B,∠C的对边分别为a,b,c,若∠B=90°,则( )
A.b2=a2+c2 B.c2=a2+b2 C.a2=b2+c2 D.a+b=c
2.以下列线段的长为三边的三角形中,能构成直角三角形的是( )
A.32,42,52 B.13,5,12
C.,, D.3,4,5
3.下列各组数中,不能作为直角三角形三边长的是( )
A.1,2, B.6,8,10 C.5,12,16 D.3,4,5
4.用四个边长均为a、b、c的直角三角板,拼成如图中所示的图形,则下列结论中正确的是( )
A.c2=a2+b2 B.c2=a2+2ab+b2
C.c2=a2﹣2ab+b2 D.c2=(a+b)2.
5.下列几组数中,是勾股数的是( )
A.1,, B.15,8,17 C.13,14,15 D.,,1
6.说明“若a是实数,则a2>0”是假命题,可以举的反例是( )
A.a=﹣1 B.a=1 C.a=0 D.a=2
7.小颖家在学校正东600米,小丽家在学校正北800米,小颖和小丽家的直线距离为( )
A.600米 B.800米 C.1000米 D.不能确定
8.给出下列四个说法:
①由于0.3,0.4,0.5不是勾股数,所以以0.3,0.4,0.5为边长的三角形不是直角三角形;
②由于以0.5,1.2,1.3为边长的三角形是直角三角形,所以0.5,1.2,1.3是勾股数;
③若a,b,c是勾股数,且c最大,则一定有a2+b2=c2;
④若三个整数a,b,c是直角三角形的三边长,则2a,2b,2c一定是勾股数,其中正确的是( )
A.①② B.②③ C.③④ D.①④
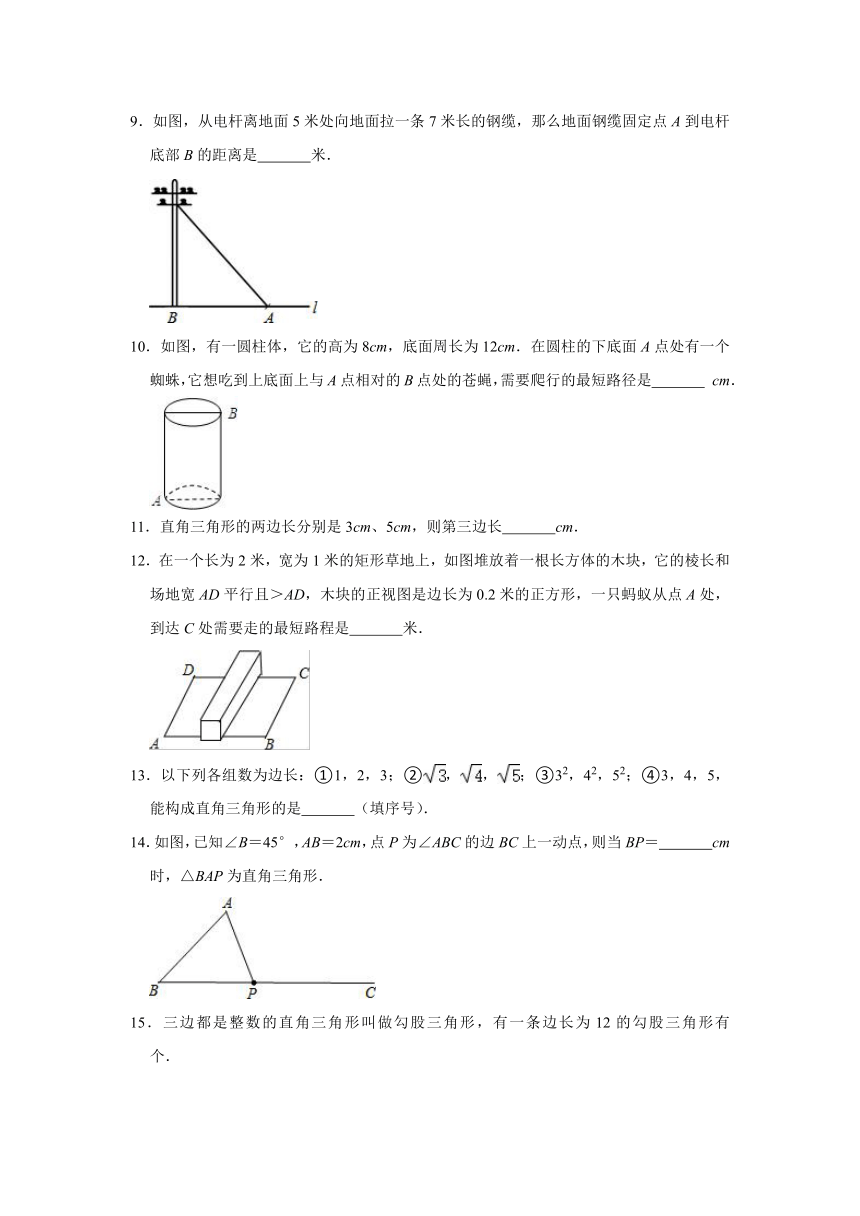
9.如图,从电杆离地面5米处向地面拉一条7米长的钢缆,那么地面钢缆固定点A到电杆底部B的距离是 米.
10.如图,有一圆柱体,它的高为8cm,底面周长为12cm.在圆柱的下底面A点处有一个蜘蛛,它想吃到上底面上与A点相对的B点处的苍蝇,需要爬行的最短路径是 cm.
11.直角三角形的两边长分别是3cm、5cm,则第三边长 cm.
12.在一个长为2米,宽为1米的矩形草地上,如图堆放着一根长方体的木块,它的棱长和场地宽AD平行且>AD,木块的正视图是边长为0.2米的正方形,一只蚂蚁从点A处,到达C处需要走的最短路程是 米.
13.以下列各组数为边长:①1,2,3;②,,;③32,42,52;④3,4,5,能构成直角三角形的是 (填序号).
14.如图,已知∠B=45°,AB=2cm,点P为∠ABC的边BC上一动点,则当BP= cm时,△BAP为直角三角形.
15.三边都是整数的直角三角形叫做勾股三角形,有一条边长为12的勾股三角形有 个.
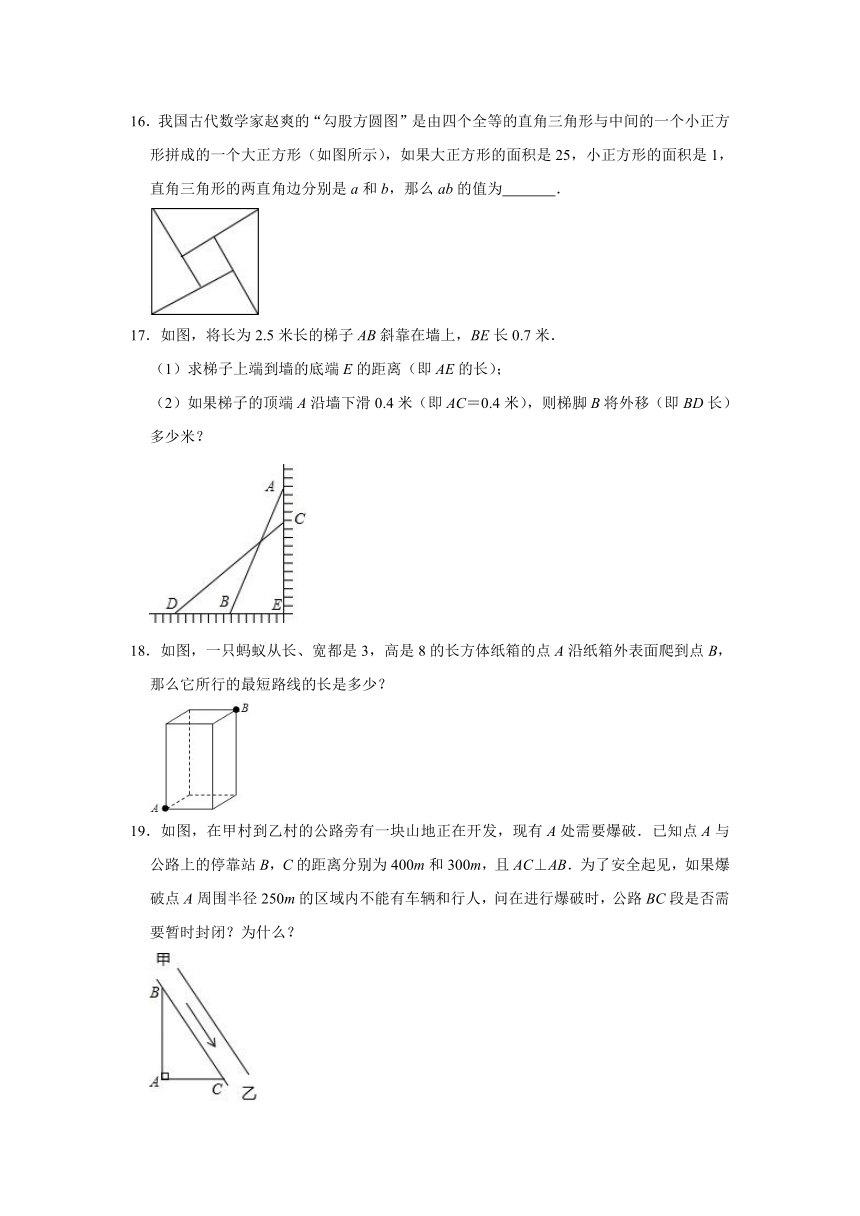
16.我国古代数学家赵爽的“勾股方圆图”是由四个全等的直角三角形与中间的一个小正方形拼成的一个大正方形(如图所示),如果大正方形的面积是25,小正方形的面积是1,直角三角形的两直角边分别是a和b,那么ab的值为 .
17.如图,将长为2.5米长的梯子AB斜靠在墙上,BE长0.7米.
(1)求梯子上端到墙的底端E的距离(即AE的长);
(2)如果梯子的顶端A沿墙下滑0.4米(即AC=0.4米),则梯脚B将外移(即BD长)多少米?
18.如图,一只蚂蚁从长、宽都是3,高是8的长方体纸箱的点A沿纸箱外表面爬到点B,那么它所行的最短路线的长是多少?
19.如图,在甲村到乙村的公路旁有一块山地正在开发,现有A处需要爆破.已知点A与公路上的停靠站B,C的距离分别为400m和300m,且AC⊥AB.为了安全起见,如果爆破点A周围半径250m的区域内不能有车辆和行人,问在进行爆破时,公路BC段是否需要暂时封闭?为什么?
20.如图,已知Rt△ABC的两条直角边BC,AC的长分别为a,b,斜边AB的长为c,斜边上的高CD的长为h.求证:.
21.判断由线段a,b,c组成的三角形是不是直角三角形:
(1)a=7,b=24,c=25;
(2)a=,b=4,c=5;
(3)a=,b=1,c=;
(4)a=40,b=50,c=60.
22.如图,在△ABC中,∠ACB是钝角,过A点作BC边上的高,垂足为D.已AB=17,BC=9,AC=10,求CD的长.
23.如图,一个长方体形的木柜放在墙角处(与墙面和地面均没有缝隙),有一只蚂蚁从柜角A处沿着木柜表面爬到柜角C1处.
(1)请你画出蚂蚁能够最快到达目的地的可能路径;
(2)当AB=4,BC=4,CC1=5时,求蚂蚁爬过的最短路径的长.
24.如图,学校为美化校园,将形状是直角三角形的﹣园地△ABC,分别以三边AB、BC、CA为直径向外作半圆,开辟为三个花坛甲、乙、丙,现分给201班同学种花.班长准备让人数相等的两个小组同学负责.为了公平分配任务,她安排一个小组负责花坛甲,另一个小组负责花坛乙和丙.你认为班长的安排合理吗?请说明理由.
试题解析和参考答案
1.解:∵∠B=90°,
∴∠B的对边b是斜边,
∴b2=a2+c2.
故选:A.
2.解:A、(32)2+(42)2≠(52)2,故不能构成直角三角形;
B、52+122=132,故能构成直角三角形;
C、()2+()2≠()2,故不能构成直角三角形;
D、(3)2+(4)2≠(5)2,故不能构成直角三角形.
故选:B.
3.解:12+22=()2,故选项A不符合题意;
62+82=102,故选项B不符合题意;
52+122≠162,故选项C符合题意;
32+42=52,故选项D不符合题意;
故选:C.
4.解:由题意得到四个完全一样的直角三角板围成的四边形为正方形,其边长为c,
里边的小四边形也为正方形,边长为b﹣a,
则有c2=ab×4+(b﹣a)2,
整理得:c2=a2+b2.
故选:A.
5.解:A、∵1,,不都是整数,∴此选项不符合题意;
B、∵152+82=172,且15,8,17都是整数,∴此选项符合题意;
C、∵132+142≠152,∴此选项符合题意;
D、∵,,1不都是整数,∴此选项不符合题意.
故选:B.
6.解:当a=0时,a2=0,则a2>0不成立;
故选:C.
7.解:如图:OA=600m,OB=800m,根据勾股定理得:AB==1000m.
故选:C.
8.解:①由于0.32+0.42=0.52,所以以0.3,0.4,0.5为边长的三角形是直角三角形,但是0.3,0.4,0.5不是整数,所以0.3,0.4,0.5不是勾股数,故①说法错误;
②虽然以0.5,1.2,1.3为边长的三角形是直角三角形,但是0.5,1.2,1.3不是整数,所以0.5,1.2,1.3不是勾股数,故②说法错误;
③若a,b,c是勾股数,且c最大,则一定有a2+b2=c2,故③说法正确;
④若三个整数a,b,c是直角三角形的三边长,则2a,2b,2c一定是勾股数,故④说法正确.
故选:C.
9.解:地面钢缆固定点A到电杆底部B的距离为
AB===2
故答案为:2.
10.解:如图,把圆柱的侧面展开,得到如图所示的图形,
其中AC=6cm,BC=8cm,
在Rt△ABC中,AB==10cm.
故答案为:10.
11.解:①当3cm和5cm都是直角边时,第三边为斜边,
由勾股定理得:第三边为=(cm);
②当3cm为直角边和5cm为斜边时,第三边为直角边,
由勾股定理得:第三边为=4(cm).
故答案为:4或.
12.解:由题意可知,将木块展开,
相当于是AB+2个正方形的宽,
∴长为2+0.2×2=2.4米;宽为1米.
于是最短路径为:=2.6米.
故答案为:2.6
13.解:①12+22=5≠32,
②()2+()2=7≠()2,
③(32)2+(42)2≠(52)2,
④32+42=52;
所以第④组能构成直角三角形,
故答案为:④.
14.解:当∠APB=90°时,
∵∠B=45°,AB=2cm,
∴BP1=AP1,
∴P1B2+P1A2=4,
∴BP1=;
当∠BAP=90°时,
∵∠B=45°,AB=2cm,
∴AB=AP2=2,
∴BP2===2.
故答案为:或2.
15.解:设另两边为a,b(a>b)
①若12为斜边,则a2+b2=122无正整数解.
②若12为直角边,则a2﹣b2=122
∴(a+b)(a﹣b)=144
∴a+b=72,a﹣b=2,
或a+b=36,a﹣b=4,
或a+b=24,a﹣b=6,
或a+b=18,a﹣b=8,
∴a=37,b=35
或a=20,b=16
或a=15,b=9
或a=13,b=5,
∴以12为一边的勾股三角形三边分别为5,12,13;9,12,15;12,16,20;12,35,37,有4个,
故答案为:4.
16.解:∵大正方形的面积是25,小正方形的面积是1,
∴直角三角形的面积是(25﹣1)÷4=6,
又∵直角三角形的面积是 ab=6,
∴ab=12.
故答案为:12.
17.解:(1)由题意得:AB=2.5米,BE=0.7米,
∵AE2=AB2﹣BE2,
∴AE==2.4米;
(2)由题意得:EC=2.4﹣0.4=2(米),
∵DE2=CD2﹣CE2,
∴DE==1.5(米),
∴BD=0.8米.
18.解:如图(1)所示:
AB==;
如图(2)所示:
AB==10.
∵>10,
∴最短路径为10.
答:它所行的最短路线的长是10.
19.解:需要暂时封闭,
理由:如图,过点A作AD⊥CB于点D.
在Rt△ABC中,由勾股定理,得:BC2=AB2+AC2=3002+4002=250000,
所以BC=500m,
由S△ABC=AB AC=BC AD,
得500×AD=300×400,
解得AD=240m,
因为240<250,所以爆破公路BC段有危险,需要暂时封锁.
20.证明:根据题意知,c≠0.
由勾股定理得到:a2+b2=c2.
又∵ab=ch,
∴ab=ch.
∴+===.即.
21.解:(1)72+242=252,符合勾股定理的逆定理,是直角三角形;
(2)42+52=()2,符合勾股定理的逆定理,是直角三角形;
(3)C、12+()2=()2,符合勾股定理的逆定理,是直角三角形;
(4)402+502≠602,不符合勾股定理的逆定理,不是直角三角形.
22.解:设AD=x,BD=y,
在直角△ADB中,AB2=x2+y2,即172=x2+y2,
在直角△ADC中,AC2=x2+(y﹣BC)2,即102=x2+(y﹣9)2,
解方程得 y=15,
∴CD=BD﹣BC=15﹣9=6.
23.解:(1)如图,
木柜的表面展开图是矩形ABC'1D1或ACC1A1.
故蚂蚁能够最快到达目的地的可能路径有如图的AC'1或AC1;
(2)蚂蚁沿着木柜表面矩形ABC'1D1爬过的路径AC'1的长是l1=.
蚂蚁沿着木柜表面矩形矩形AB1C1D爬过的路径AC1的长l1=,
蚂蚁沿着木柜表面ACC1A1爬过的路径AC1的长是l2=.
l1>l2,故最短路径的长是l2=.
24.解:班长的安排合理.理由如下:
∵S甲=π×()2
S乙=π×()2
S丙=π×()2
又△ABC是直角三角形
∴=+
∴S甲=S乙+S丙
答:因为班长分配给两个小组的花坛面积相等,所以她的安排是合理的。
《第14章勾股定理》期末综合复习训练题
1.已知Rt△ABC中,∠A,∠B,∠C的对边分别为a,b,c,若∠B=90°,则( )
A.b2=a2+c2 B.c2=a2+b2 C.a2=b2+c2 D.a+b=c
2.以下列线段的长为三边的三角形中,能构成直角三角形的是( )
A.32,42,52 B.13,5,12
C.,, D.3,4,5
3.下列各组数中,不能作为直角三角形三边长的是( )
A.1,2, B.6,8,10 C.5,12,16 D.3,4,5
4.用四个边长均为a、b、c的直角三角板,拼成如图中所示的图形,则下列结论中正确的是( )
A.c2=a2+b2 B.c2=a2+2ab+b2
C.c2=a2﹣2ab+b2 D.c2=(a+b)2.
5.下列几组数中,是勾股数的是( )
A.1,, B.15,8,17 C.13,14,15 D.,,1
6.说明“若a是实数,则a2>0”是假命题,可以举的反例是( )
A.a=﹣1 B.a=1 C.a=0 D.a=2
7.小颖家在学校正东600米,小丽家在学校正北800米,小颖和小丽家的直线距离为( )
A.600米 B.800米 C.1000米 D.不能确定
8.给出下列四个说法:
①由于0.3,0.4,0.5不是勾股数,所以以0.3,0.4,0.5为边长的三角形不是直角三角形;
②由于以0.5,1.2,1.3为边长的三角形是直角三角形,所以0.5,1.2,1.3是勾股数;
③若a,b,c是勾股数,且c最大,则一定有a2+b2=c2;
④若三个整数a,b,c是直角三角形的三边长,则2a,2b,2c一定是勾股数,其中正确的是( )
A.①② B.②③ C.③④ D.①④
9.如图,从电杆离地面5米处向地面拉一条7米长的钢缆,那么地面钢缆固定点A到电杆底部B的距离是 米.
10.如图,有一圆柱体,它的高为8cm,底面周长为12cm.在圆柱的下底面A点处有一个蜘蛛,它想吃到上底面上与A点相对的B点处的苍蝇,需要爬行的最短路径是 cm.
11.直角三角形的两边长分别是3cm、5cm,则第三边长 cm.
12.在一个长为2米,宽为1米的矩形草地上,如图堆放着一根长方体的木块,它的棱长和场地宽AD平行且>AD,木块的正视图是边长为0.2米的正方形,一只蚂蚁从点A处,到达C处需要走的最短路程是 米.
13.以下列各组数为边长:①1,2,3;②,,;③32,42,52;④3,4,5,能构成直角三角形的是 (填序号).
14.如图,已知∠B=45°,AB=2cm,点P为∠ABC的边BC上一动点,则当BP= cm时,△BAP为直角三角形.
15.三边都是整数的直角三角形叫做勾股三角形,有一条边长为12的勾股三角形有 个.
16.我国古代数学家赵爽的“勾股方圆图”是由四个全等的直角三角形与中间的一个小正方形拼成的一个大正方形(如图所示),如果大正方形的面积是25,小正方形的面积是1,直角三角形的两直角边分别是a和b,那么ab的值为 .
17.如图,将长为2.5米长的梯子AB斜靠在墙上,BE长0.7米.
(1)求梯子上端到墙的底端E的距离(即AE的长);
(2)如果梯子的顶端A沿墙下滑0.4米(即AC=0.4米),则梯脚B将外移(即BD长)多少米?
18.如图,一只蚂蚁从长、宽都是3,高是8的长方体纸箱的点A沿纸箱外表面爬到点B,那么它所行的最短路线的长是多少?
19.如图,在甲村到乙村的公路旁有一块山地正在开发,现有A处需要爆破.已知点A与公路上的停靠站B,C的距离分别为400m和300m,且AC⊥AB.为了安全起见,如果爆破点A周围半径250m的区域内不能有车辆和行人,问在进行爆破时,公路BC段是否需要暂时封闭?为什么?
20.如图,已知Rt△ABC的两条直角边BC,AC的长分别为a,b,斜边AB的长为c,斜边上的高CD的长为h.求证:.
21.判断由线段a,b,c组成的三角形是不是直角三角形:
(1)a=7,b=24,c=25;
(2)a=,b=4,c=5;
(3)a=,b=1,c=;
(4)a=40,b=50,c=60.
22.如图,在△ABC中,∠ACB是钝角,过A点作BC边上的高,垂足为D.已AB=17,BC=9,AC=10,求CD的长.
23.如图,一个长方体形的木柜放在墙角处(与墙面和地面均没有缝隙),有一只蚂蚁从柜角A处沿着木柜表面爬到柜角C1处.
(1)请你画出蚂蚁能够最快到达目的地的可能路径;
(2)当AB=4,BC=4,CC1=5时,求蚂蚁爬过的最短路径的长.
24.如图,学校为美化校园,将形状是直角三角形的﹣园地△ABC,分别以三边AB、BC、CA为直径向外作半圆,开辟为三个花坛甲、乙、丙,现分给201班同学种花.班长准备让人数相等的两个小组同学负责.为了公平分配任务,她安排一个小组负责花坛甲,另一个小组负责花坛乙和丙.你认为班长的安排合理吗?请说明理由.
试题解析和参考答案
1.解:∵∠B=90°,
∴∠B的对边b是斜边,
∴b2=a2+c2.
故选:A.
2.解:A、(32)2+(42)2≠(52)2,故不能构成直角三角形;
B、52+122=132,故能构成直角三角形;
C、()2+()2≠()2,故不能构成直角三角形;
D、(3)2+(4)2≠(5)2,故不能构成直角三角形.
故选:B.
3.解:12+22=()2,故选项A不符合题意;
62+82=102,故选项B不符合题意;
52+122≠162,故选项C符合题意;
32+42=52,故选项D不符合题意;
故选:C.
4.解:由题意得到四个完全一样的直角三角板围成的四边形为正方形,其边长为c,
里边的小四边形也为正方形,边长为b﹣a,
则有c2=ab×4+(b﹣a)2,
整理得:c2=a2+b2.
故选:A.
5.解:A、∵1,,不都是整数,∴此选项不符合题意;
B、∵152+82=172,且15,8,17都是整数,∴此选项符合题意;
C、∵132+142≠152,∴此选项符合题意;
D、∵,,1不都是整数,∴此选项不符合题意.
故选:B.
6.解:当a=0时,a2=0,则a2>0不成立;
故选:C.
7.解:如图:OA=600m,OB=800m,根据勾股定理得:AB==1000m.
故选:C.
8.解:①由于0.32+0.42=0.52,所以以0.3,0.4,0.5为边长的三角形是直角三角形,但是0.3,0.4,0.5不是整数,所以0.3,0.4,0.5不是勾股数,故①说法错误;
②虽然以0.5,1.2,1.3为边长的三角形是直角三角形,但是0.5,1.2,1.3不是整数,所以0.5,1.2,1.3不是勾股数,故②说法错误;
③若a,b,c是勾股数,且c最大,则一定有a2+b2=c2,故③说法正确;
④若三个整数a,b,c是直角三角形的三边长,则2a,2b,2c一定是勾股数,故④说法正确.
故选:C.
9.解:地面钢缆固定点A到电杆底部B的距离为
AB===2
故答案为:2.
10.解:如图,把圆柱的侧面展开,得到如图所示的图形,
其中AC=6cm,BC=8cm,
在Rt△ABC中,AB==10cm.
故答案为:10.
11.解:①当3cm和5cm都是直角边时,第三边为斜边,
由勾股定理得:第三边为=(cm);
②当3cm为直角边和5cm为斜边时,第三边为直角边,
由勾股定理得:第三边为=4(cm).
故答案为:4或.
12.解:由题意可知,将木块展开,
相当于是AB+2个正方形的宽,
∴长为2+0.2×2=2.4米;宽为1米.
于是最短路径为:=2.6米.
故答案为:2.6
13.解:①12+22=5≠32,
②()2+()2=7≠()2,
③(32)2+(42)2≠(52)2,
④32+42=52;
所以第④组能构成直角三角形,
故答案为:④.
14.解:当∠APB=90°时,
∵∠B=45°,AB=2cm,
∴BP1=AP1,
∴P1B2+P1A2=4,
∴BP1=;
当∠BAP=90°时,
∵∠B=45°,AB=2cm,
∴AB=AP2=2,
∴BP2===2.
故答案为:或2.
15.解:设另两边为a,b(a>b)
①若12为斜边,则a2+b2=122无正整数解.
②若12为直角边,则a2﹣b2=122
∴(a+b)(a﹣b)=144
∴a+b=72,a﹣b=2,
或a+b=36,a﹣b=4,
或a+b=24,a﹣b=6,
或a+b=18,a﹣b=8,
∴a=37,b=35
或a=20,b=16
或a=15,b=9
或a=13,b=5,
∴以12为一边的勾股三角形三边分别为5,12,13;9,12,15;12,16,20;12,35,37,有4个,
故答案为:4.
16.解:∵大正方形的面积是25,小正方形的面积是1,
∴直角三角形的面积是(25﹣1)÷4=6,
又∵直角三角形的面积是 ab=6,
∴ab=12.
故答案为:12.
17.解:(1)由题意得:AB=2.5米,BE=0.7米,
∵AE2=AB2﹣BE2,
∴AE==2.4米;
(2)由题意得:EC=2.4﹣0.4=2(米),
∵DE2=CD2﹣CE2,
∴DE==1.5(米),
∴BD=0.8米.
18.解:如图(1)所示:
AB==;
如图(2)所示:
AB==10.
∵>10,
∴最短路径为10.
答:它所行的最短路线的长是10.
19.解:需要暂时封闭,
理由:如图,过点A作AD⊥CB于点D.
在Rt△ABC中,由勾股定理,得:BC2=AB2+AC2=3002+4002=250000,
所以BC=500m,
由S△ABC=AB AC=BC AD,
得500×AD=300×400,
解得AD=240m,
因为240<250,所以爆破公路BC段有危险,需要暂时封锁.
20.证明:根据题意知,c≠0.
由勾股定理得到:a2+b2=c2.
又∵ab=ch,
∴ab=ch.
∴+===.即.
21.解:(1)72+242=252,符合勾股定理的逆定理,是直角三角形;
(2)42+52=()2,符合勾股定理的逆定理,是直角三角形;
(3)C、12+()2=()2,符合勾股定理的逆定理,是直角三角形;
(4)402+502≠602,不符合勾股定理的逆定理,不是直角三角形.
22.解:设AD=x,BD=y,
在直角△ADB中,AB2=x2+y2,即172=x2+y2,
在直角△ADC中,AC2=x2+(y﹣BC)2,即102=x2+(y﹣9)2,
解方程得 y=15,
∴CD=BD﹣BC=15﹣9=6.
23.解:(1)如图,
木柜的表面展开图是矩形ABC'1D1或ACC1A1.
故蚂蚁能够最快到达目的地的可能路径有如图的AC'1或AC1;
(2)蚂蚁沿着木柜表面矩形ABC'1D1爬过的路径AC'1的长是l1=.
蚂蚁沿着木柜表面矩形矩形AB1C1D爬过的路径AC1的长l1=,
蚂蚁沿着木柜表面ACC1A1爬过的路径AC1的长是l2=.
l1>l2,故最短路径的长是l2=.
24.解:班长的安排合理.理由如下:
∵S甲=π×()2
S乙=π×()2
S丙=π×()2
又△ABC是直角三角形
∴=+
∴S甲=S乙+S丙
答:因为班长分配给两个小组的花坛面积相等,所以她的安排是合理的。
