2.1.1椭圆及其标准方程
图片预览







文档简介
课件24张PPT。第二章 圆锥曲线与方程
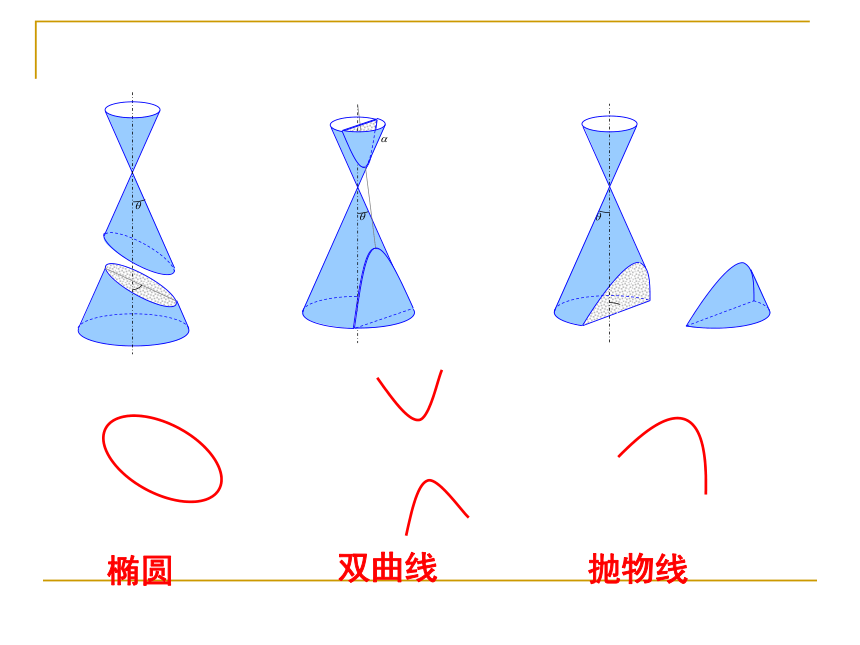
§2.1.1 椭圆及其标准方程 用一个平面去截一个圆锥面,当平面经过圆锥面的顶点时,可得到 ;当平面与圆锥面的轴垂直时,截线(平面与圆锥面的交线)是一个 .
当改变截面与圆锥面的轴的相对位置时,观察截线的变化情况,并思考:
● 用平面截圆锥面还能得到哪些曲线?这些曲线具有哪些几何特征?
两条相交直线圆
椭圆双曲线抛物线一、引入结论:平面内到两定点F1,F2的距离之和等于常数的点的轨迹为椭圆。常数必须大于两定点的距离1、椭圆的定义: 平面内到两个定点F1、F2的距离之和等于常数(大于|F1F2|)的动点M的轨迹叫做椭圆。 这两个定点叫做椭圆的焦点,两焦点间的距离叫做椭圆的焦距|F1F2|=2c 。几点说明:1、椭圆定义式:|MF1| + |MF2| = 2a > |F1F2|=2c.则M点的轨迹是椭圆.2、若|MF1| + |MF2| = 2a = |F1F2|=2c ,则M点的轨迹是线段F1F2.3、若|MF1| + |MF2| = 2a < |F1F2|=2c ,则M点的轨迹不存在.二、讲授新课应用举例例1.用定义判断下列动点M的轨迹是否为椭圆。(1)到F1(-2,0)、F2(2,0)的距离之和为6的点的轨迹。(2)到F1(0,-2)、F2(0,2)的距离之和为4的点的轨迹。(3)到F1(-2,0)、F2(2,0)的距离之和为3的点的轨迹。解 (1)因|MF1|+|MF2|=6>|F1F2|=4,故点M的轨迹为椭圆。(2)因|MF1|+|MF2|=4=|F1F2|=4,故点M的轨迹不是椭圆(是线段F1F2)。(3)因|MF1|+|MF2|=3<|F1F2|=4,故点M的轨迹不成图形。OxyF1F2M如图所示: F1、F2为两定点,且|F1F2|=2c,求平面内到两定点F1、F2距离之和为定值2a(2a>2c)的动点M的轨迹方程。解:以F1F2所在直线为X轴,线段F1F2 的垂直平分线为Y轴,建立平面直角坐标系,则焦点F1、F2的坐标分别为(-c,0)、 (c,0)。(-c,0)(c,0)(x,y) 设M(x,y)为所求轨迹上的任意一点,则:|MF1|+ |MF2|=2a 且2a>2c2、椭圆标准方程及其推导求曲线轨迹方程的步骤:1、建系 2、设标 3、列式 4、化简 5、检验(可省略不写)OXYF1F2M(-c,0)(c,0)(x,y)两边平方得:a4-2a2cx+c2x2=a2x2-2a2cx+a2c2+a2y2即:(a2-c2)x2+a2y2=a2(a2-c2)因为2a>2c,即a>c,所以a2-c2>0,令a2-c2=b2,其中b>0,代入上式可得:b2x2+a2y2=a2b2两边同时除以a2b2得:(a>b>0)这个方程叫做椭圆的标准方程,
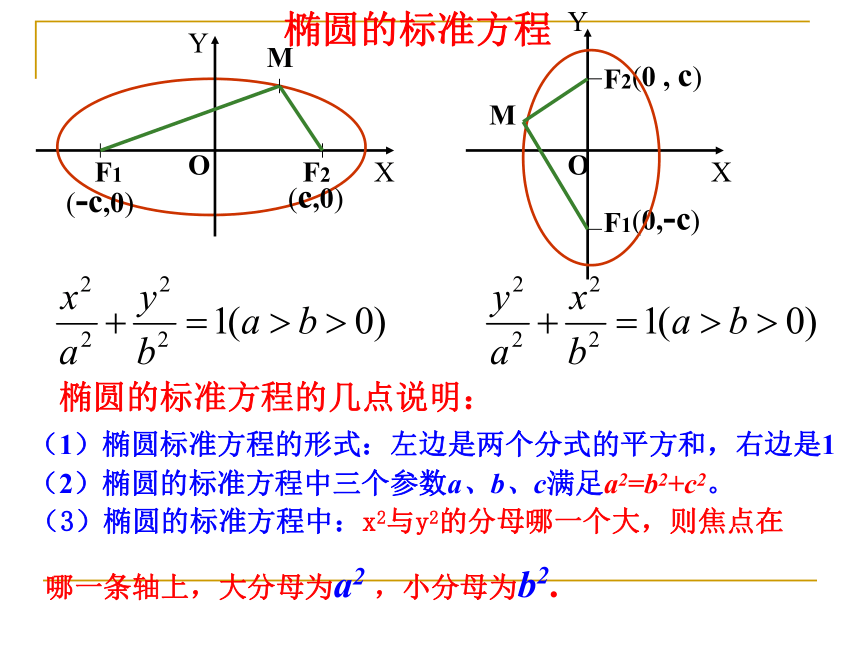
它所表示的椭圆的焦点在x 轴上。acbOXYF1F2M(-c,0)(c,0)OXYF1F2M(0,-c)(0 , c)椭圆的标准方程的几点说明:(1)椭圆标准方程的形式:左边是两个分式的平方和,右边是1(2)椭圆的标准方程中三个参数a、b、c满足a2=b2+c2。(3)椭圆的标准方程中:x2与y2的分母哪一个大,则焦点在
哪一条轴上,大分母为a2 ,小分母为b2.椭圆的标准方程分母哪个大,焦点就在哪个轴上a2-c2=b23、椭圆的标准方程小结|MF1|+|MF2|=2a (2a>2c>0)例3、椭圆的两个焦点的坐标分别是(-4,0),(4,0),椭圆上一点P到两焦点距离之和等于10,求椭圆的标准方程。 例4、动点P到两定点F1(-4,0),F2(4,0)的距离之和为8,则动点P的轨迹为( ) A.椭圆 B.线段F1F2 C.直线F1F2 D.不能确定
B例5、椭圆 上一点P到一个焦点的距离等于3,则它到另一个焦点的距离是( )
A.5 B.7 C.8 D.2B例6、动点P到两定点F1(-4,0),F2(4,0)的距离和是7,则动点P的轨迹为( )A.椭圆 B.线段F1F2 C.直线F1F2 D.无轨迹D解法一:因为椭圆的焦点在x轴上,所以设它的标准方程为由椭圆的定义知因此, 所求椭圆的标准方程为解法二:因为椭圆的焦点在x轴上,所以设它的标准方程为①②联立①②,因此, 所求椭圆的标准方程为求椭圆标准方程的解题步骤:(1)确定焦点的位置;(2)设出椭圆的标准方程;(3)用待定系数法确定a、b的值,
写出椭圆的标准方程.例3.椭圆的两个焦点的坐标分别是(-4,0)
(4,0),椭圆上一点P到两焦点距离之和等于10,
求椭圆的标准方程。 解: ∵椭圆的焦点在x轴上
∴设它的标准方程为:
∵ 2a=10, 2c=8
∴ a=5, c=4
∴ b2=a2-c2=52-42=9
∴所求椭圆的标准方程为
1、建系 2、设标 3、列式 4、化简 5、检验(可省略不写)例5、如图,设点A,B的坐标分别为(-5,0),(5,0)。
直线AM,BM相交于点M,且它们的斜率之积是
,求点M的轨迹方程。解:设点M的坐标为(x,y),因为点A的坐标是,所以直线
AM的斜率同理,直线BM的斜率由已知有化简,得点M的轨迹方程为椭圆的一般形式例6、(1)求椭圆的标准方程: 经过点P(- ,2),Q( ,- )(2)已知一椭圆的焦距为2 ,且经
过点(2,2),求椭圆的标准方程。填空:
(1)已知椭圆的方程为: ,则a=_____,b=_______,c=_______,焦点坐标为:____________焦距等于______;若CD为过左焦点F1的弦,则?F2CD的周长为________课前练习543(3,0)、(-3,0)620判断椭圆标准方程的焦点在哪个轴上的准则:
焦点在分母大的那个轴上。|CF1|+|CF2|=2a(2)已知椭圆的方程为: ,则
a=_____,b=_______,c=_______,
焦点坐标为:__________,焦距
等于_________;
若曲线上一点P到焦点F1的距离为3,则
点P到另一个焦点F2的距离等于_________,
则?F1PF2的周长为___________21(0,-1)、(0,1)2P|PF1|+|PF2|=2a课后练习: 1 化简方程:4 设F1,F2为定点,|F1F2|=6,动点M满足
|MF1|+ |MF2|=6,则动点的轨迹是( )
(A)椭圆 (B)直线
(C)线段 (D)圆
5 如果方程x2+ky2=2表示焦点在y轴上的椭圆,
则k的取值范围是_______
0
§2.1.1 椭圆及其标准方程 用一个平面去截一个圆锥面,当平面经过圆锥面的顶点时,可得到 ;当平面与圆锥面的轴垂直时,截线(平面与圆锥面的交线)是一个 .
当改变截面与圆锥面的轴的相对位置时,观察截线的变化情况,并思考:
● 用平面截圆锥面还能得到哪些曲线?这些曲线具有哪些几何特征?
两条相交直线圆
椭圆双曲线抛物线一、引入结论:平面内到两定点F1,F2的距离之和等于常数的点的轨迹为椭圆。常数必须大于两定点的距离1、椭圆的定义: 平面内到两个定点F1、F2的距离之和等于常数(大于|F1F2|)的动点M的轨迹叫做椭圆。 这两个定点叫做椭圆的焦点,两焦点间的距离叫做椭圆的焦距|F1F2|=2c 。几点说明:1、椭圆定义式:|MF1| + |MF2| = 2a > |F1F2|=2c.则M点的轨迹是椭圆.2、若|MF1| + |MF2| = 2a = |F1F2|=2c ,则M点的轨迹是线段F1F2.3、若|MF1| + |MF2| = 2a < |F1F2|=2c ,则M点的轨迹不存在.二、讲授新课应用举例例1.用定义判断下列动点M的轨迹是否为椭圆。(1)到F1(-2,0)、F2(2,0)的距离之和为6的点的轨迹。(2)到F1(0,-2)、F2(0,2)的距离之和为4的点的轨迹。(3)到F1(-2,0)、F2(2,0)的距离之和为3的点的轨迹。解 (1)因|MF1|+|MF2|=6>|F1F2|=4,故点M的轨迹为椭圆。(2)因|MF1|+|MF2|=4=|F1F2|=4,故点M的轨迹不是椭圆(是线段F1F2)。(3)因|MF1|+|MF2|=3<|F1F2|=4,故点M的轨迹不成图形。OxyF1F2M如图所示: F1、F2为两定点,且|F1F2|=2c,求平面内到两定点F1、F2距离之和为定值2a(2a>2c)的动点M的轨迹方程。解:以F1F2所在直线为X轴,线段F1F2 的垂直平分线为Y轴,建立平面直角坐标系,则焦点F1、F2的坐标分别为(-c,0)、 (c,0)。(-c,0)(c,0)(x,y) 设M(x,y)为所求轨迹上的任意一点,则:|MF1|+ |MF2|=2a 且2a>2c2、椭圆标准方程及其推导求曲线轨迹方程的步骤:1、建系 2、设标 3、列式 4、化简 5、检验(可省略不写)OXYF1F2M(-c,0)(c,0)(x,y)两边平方得:a4-2a2cx+c2x2=a2x2-2a2cx+a2c2+a2y2即:(a2-c2)x2+a2y2=a2(a2-c2)因为2a>2c,即a>c,所以a2-c2>0,令a2-c2=b2,其中b>0,代入上式可得:b2x2+a2y2=a2b2两边同时除以a2b2得:(a>b>0)这个方程叫做椭圆的标准方程,
它所表示的椭圆的焦点在x 轴上。acbOXYF1F2M(-c,0)(c,0)OXYF1F2M(0,-c)(0 , c)椭圆的标准方程的几点说明:(1)椭圆标准方程的形式:左边是两个分式的平方和,右边是1(2)椭圆的标准方程中三个参数a、b、c满足a2=b2+c2。(3)椭圆的标准方程中:x2与y2的分母哪一个大,则焦点在
哪一条轴上,大分母为a2 ,小分母为b2.椭圆的标准方程分母哪个大,焦点就在哪个轴上a2-c2=b23、椭圆的标准方程小结|MF1|+|MF2|=2a (2a>2c>0)例3、椭圆的两个焦点的坐标分别是(-4,0),(4,0),椭圆上一点P到两焦点距离之和等于10,求椭圆的标准方程。 例4、动点P到两定点F1(-4,0),F2(4,0)的距离之和为8,则动点P的轨迹为( ) A.椭圆 B.线段F1F2 C.直线F1F2 D.不能确定
B例5、椭圆 上一点P到一个焦点的距离等于3,则它到另一个焦点的距离是( )
A.5 B.7 C.8 D.2B例6、动点P到两定点F1(-4,0),F2(4,0)的距离和是7,则动点P的轨迹为( )A.椭圆 B.线段F1F2 C.直线F1F2 D.无轨迹D解法一:因为椭圆的焦点在x轴上,所以设它的标准方程为由椭圆的定义知因此, 所求椭圆的标准方程为解法二:因为椭圆的焦点在x轴上,所以设它的标准方程为①②联立①②,因此, 所求椭圆的标准方程为求椭圆标准方程的解题步骤:(1)确定焦点的位置;(2)设出椭圆的标准方程;(3)用待定系数法确定a、b的值,
写出椭圆的标准方程.例3.椭圆的两个焦点的坐标分别是(-4,0)
(4,0),椭圆上一点P到两焦点距离之和等于10,
求椭圆的标准方程。 解: ∵椭圆的焦点在x轴上
∴设它的标准方程为:
∵ 2a=10, 2c=8
∴ a=5, c=4
∴ b2=a2-c2=52-42=9
∴所求椭圆的标准方程为
1、建系 2、设标 3、列式 4、化简 5、检验(可省略不写)例5、如图,设点A,B的坐标分别为(-5,0),(5,0)。
直线AM,BM相交于点M,且它们的斜率之积是
,求点M的轨迹方程。解:设点M的坐标为(x,y),因为点A的坐标是,所以直线
AM的斜率同理,直线BM的斜率由已知有化简,得点M的轨迹方程为椭圆的一般形式例6、(1)求椭圆的标准方程: 经过点P(- ,2),Q( ,- )(2)已知一椭圆的焦距为2 ,且经
过点(2,2),求椭圆的标准方程。填空:
(1)已知椭圆的方程为: ,则a=_____,b=_______,c=_______,焦点坐标为:____________焦距等于______;若CD为过左焦点F1的弦,则?F2CD的周长为________课前练习543(3,0)、(-3,0)620判断椭圆标准方程的焦点在哪个轴上的准则:
焦点在分母大的那个轴上。|CF1|+|CF2|=2a(2)已知椭圆的方程为: ,则
a=_____,b=_______,c=_______,
焦点坐标为:__________,焦距
等于_________;
若曲线上一点P到焦点F1的距离为3,则
点P到另一个焦点F2的距离等于_________,
则?F1PF2的周长为___________21(0,-1)、(0,1)2P|PF1|+|PF2|=2a课后练习: 1 化简方程:4 设F1,F2为定点,|F1F2|=6,动点M满足
|MF1|+ |MF2|=6,则动点的轨迹是( )
(A)椭圆 (B)直线
(C)线段 (D)圆
5 如果方程x2+ky2=2表示焦点在y轴上的椭圆,
则k的取值范围是_______
0
