沪科版数学九年级上册 21.5 反比例函数课件(共21张PPT)
文档属性
| 名称 | 沪科版数学九年级上册 21.5 反比例函数课件(共21张PPT) |  | |
| 格式 | ppt | ||
| 文件大小 | 1.5MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-12-27 17:04:05 | ||
图片预览






文档简介
(共21张PPT)
20.5 反比例函数
知识回顾:
1.反比例函数的意义.
2.反比例函数的图象与性质.
3.利用反比例函数解决实际问题.
什么是反比例函数?
忆一忆:
一般地,函数 (k是常数, k ≠0)叫反
比例函数.
小试牛刀:
1.下列函数中,哪些是反比例函数?
⑴
⑵
⑶
⑷
⑸
小试牛刀:
2.写出下列问题中的函数关系式,并指出它们是什
么函数?
⑴当路程s一定时,时间t与平均速度v之间的关系.
⑵质量为m(kg)的气体,其体积v(m3)与密度
ρ(kg/m3)之间的关系.
反比例函数
反比例函数
小试牛刀:
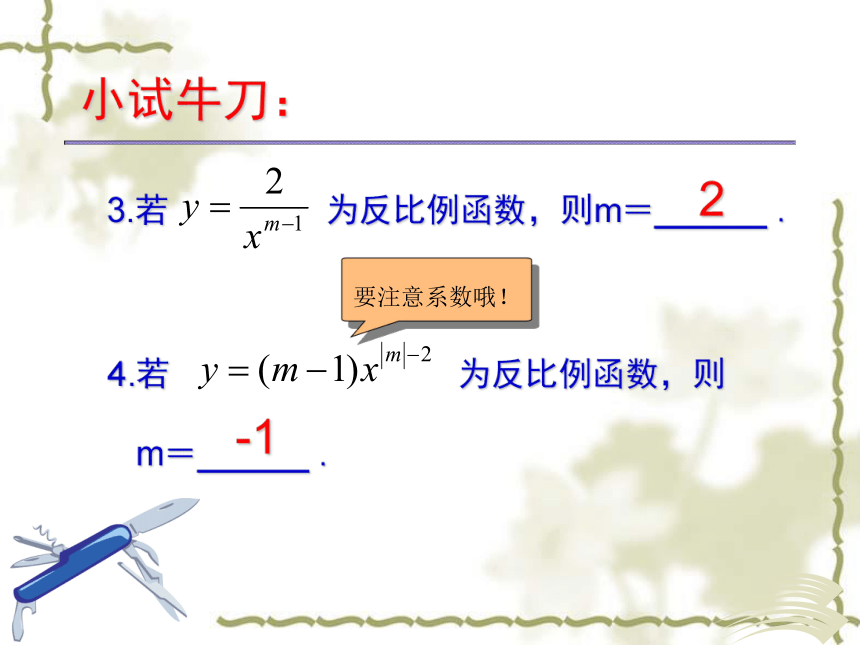
3.若 为反比例函数,则m=______ .
4.若 为反比例函数,则
m=______ .
要注意系数哦!
2
-1
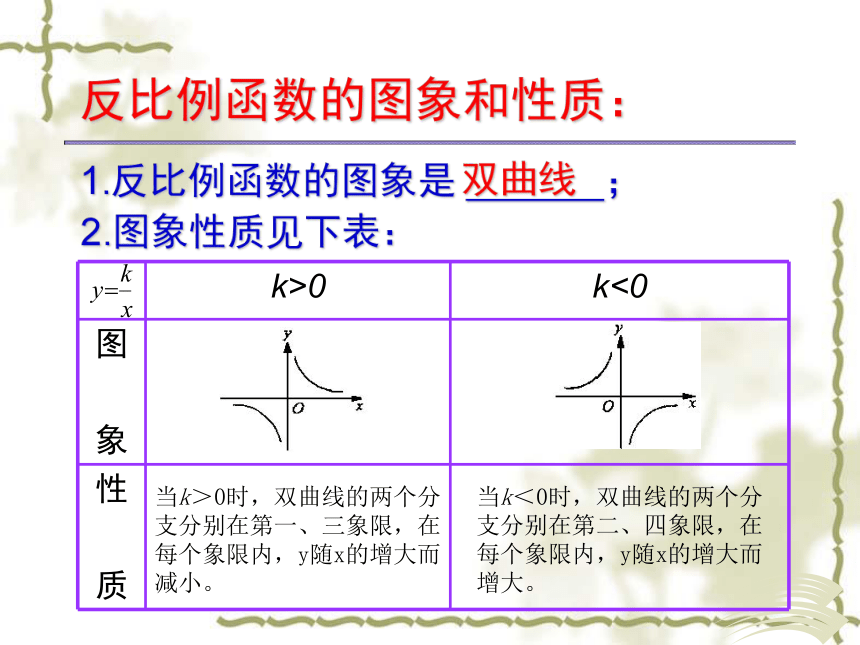
反比例函数的图象和性质:
1.反比例函数的图象是 ;
双曲线
2.图象性质见下表:
k>0 k<0
图
象
性
质
当k>0时,双曲线的两个分支分别在第一、三象限,在每个象限内,y随x的增大而减小。
当k<0时,双曲线的两个分支分别在第二、四象限,在每个象限内,y随x的增大而增大。
做一做:
1.函数 的图象在第______象限,当x<0时,
y随x的增大而______ .
2.双曲线 经过点 (-3 ,______ ).
3.函数 的图象在二、四象限内,m的取值
范围是______ .
4.若双曲线经过点(-3 ,2),则其解析式是______.
一、三
减小
1
9
m<2
6
x
y
=
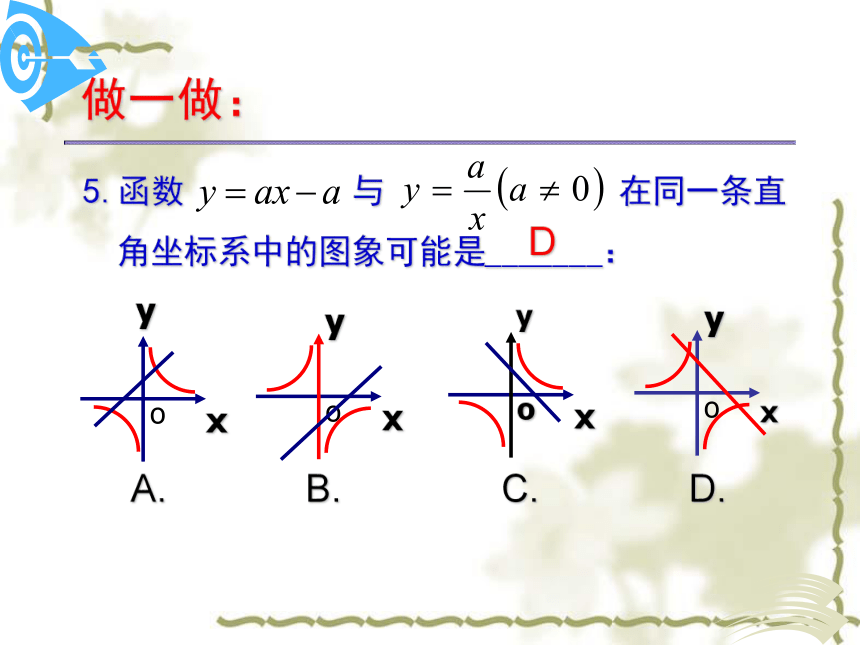
5.函数 与 在同一条直
角坐标系中的图象可能是_______:
做一做:
D
x
y
o
x
y
o
x
y
o
x
y
o
A. B. C. D.
做一做:
6.已知点A(-2,y1),B(-1,y2) C(4,y3)都在反比
例函数 的
图象上,则y1、y2 与y3
的大小关系(从大到小)
为____________ .
y
x
o
-1
y1
y2
A
B
-2
4
C
y3
y3 >y1>y2
议一议:
已知点P是x轴正半轴上的一个动点,过点P作x轴的垂线PA交双曲线 于点A,过点A作AB⊥y轴于B点。在点P
运动过程中,矩形OPAB
的面积是否发生变化?
若不变,请求出其面积;
若改变,试说明理由。
A
O
P
x
y
B
K的几何意义:
过双曲线 上一点P(m,n)分别作x轴,y轴的垂线,垂足分别为A、B,则 S矩形OAPB
.P(m,n)
A
o
y
x
B
=OA·AP=|m| ·|n|=|k|
.P(m,n)
.P(m,n)
如图,点P是反比例函数图象上的一点,过点P分别向x轴、y轴作垂线,若阴影部分面积为12,则这个反比例函数的关系式是__________ 。
变式一:
x
y
o
M
N
p
12
x
y
=
如图所示,正比例函数 与反比例函数 的图象相交于A、C两点,过A作x轴的垂线交x轴于B,连接BC.若△ABC面积为S,则______
变式二:
(A)s=1 (B) s=2
(C)1A
1. 如图:一次函数的图象 与反比例函数
交于M(2,m)、N(-1,-4)两点.
(1)求反比例函数和一
次函数的解析式;
(2)根据图象写出反比
例函数的值大于一
次函数的值的x的取
值范围.
综合运用:
M(2,m)
2
0
-1
N(-1,-4)
y
x
综合运用:
M(2,m)
2
0
-1
N(-1,-4)
y
x
(1)求反比例函数和一次函数的解析式;
解:(1)∵点N(-1,-4)在反比例函数图象上
∴k=4,
又∵点M(2,m)在反比例函数
图象上
∴m=2 ∴M(2,2)
∵点M、N都在y=ax+b的图象上
∴y= 2x-2
∴
∴
解得
综合运用:
y
x
2
0
-1
N(-1,-4)
M(2,m)
(2)根据图象写出反比例函数的值大于一次函数的值的x的取值范围.
(2)观察图象得:
当x<-1或0综合运用:
综合运用:
2.某商场出售一批进价为2元的贺卡,在市场营销中发现此商品的日销售单价x(元)与日销售量y(个)之间有如下关系:
x (元) 3 4 5 6 ……
y(个) 20 15 12 10 ……
(1)猜想并确定在赢利的条件下y与x之间的函数关系式。
(2)设经营此贺卡的销售利润为w元,试求出w与x之间的函数关系式,若物价局规定此贺卡的销售价最高不能超过10元,请你求出当销售单价x定为多少时,才能使获利最大?
……
20.5 反比例函数
知识回顾:
1.反比例函数的意义.
2.反比例函数的图象与性质.
3.利用反比例函数解决实际问题.
什么是反比例函数?
忆一忆:
一般地,函数 (k是常数, k ≠0)叫反
比例函数.
小试牛刀:
1.下列函数中,哪些是反比例函数?
⑴
⑵
⑶
⑷
⑸
小试牛刀:
2.写出下列问题中的函数关系式,并指出它们是什
么函数?
⑴当路程s一定时,时间t与平均速度v之间的关系.
⑵质量为m(kg)的气体,其体积v(m3)与密度
ρ(kg/m3)之间的关系.
反比例函数
反比例函数
小试牛刀:
3.若 为反比例函数,则m=______ .
4.若 为反比例函数,则
m=______ .
要注意系数哦!
2
-1
反比例函数的图象和性质:
1.反比例函数的图象是 ;
双曲线
2.图象性质见下表:
k>0 k<0
图
象
性
质
当k>0时,双曲线的两个分支分别在第一、三象限,在每个象限内,y随x的增大而减小。
当k<0时,双曲线的两个分支分别在第二、四象限,在每个象限内,y随x的增大而增大。
做一做:
1.函数 的图象在第______象限,当x<0时,
y随x的增大而______ .
2.双曲线 经过点 (-3 ,______ ).
3.函数 的图象在二、四象限内,m的取值
范围是______ .
4.若双曲线经过点(-3 ,2),则其解析式是______.
一、三
减小
1
9
m<2
6
x
y
=
5.函数 与 在同一条直
角坐标系中的图象可能是_______:
做一做:
D
x
y
o
x
y
o
x
y
o
x
y
o
A. B. C. D.
做一做:
6.已知点A(-2,y1),B(-1,y2) C(4,y3)都在反比
例函数 的
图象上,则y1、y2 与y3
的大小关系(从大到小)
为____________ .
y
x
o
-1
y1
y2
A
B
-2
4
C
y3
y3 >y1>y2
议一议:
已知点P是x轴正半轴上的一个动点,过点P作x轴的垂线PA交双曲线 于点A,过点A作AB⊥y轴于B点。在点P
运动过程中,矩形OPAB
的面积是否发生变化?
若不变,请求出其面积;
若改变,试说明理由。
A
O
P
x
y
B
K的几何意义:
过双曲线 上一点P(m,n)分别作x轴,y轴的垂线,垂足分别为A、B,则 S矩形OAPB
.P(m,n)
A
o
y
x
B
=OA·AP=|m| ·|n|=|k|
.P(m,n)
.P(m,n)
如图,点P是反比例函数图象上的一点,过点P分别向x轴、y轴作垂线,若阴影部分面积为12,则这个反比例函数的关系式是__________ 。
变式一:
x
y
o
M
N
p
12
x
y
=
如图所示,正比例函数 与反比例函数 的图象相交于A、C两点,过A作x轴的垂线交x轴于B,连接BC.若△ABC面积为S,则______
变式二:
(A)s=1 (B) s=2
(C)1
1. 如图:一次函数的图象 与反比例函数
交于M(2,m)、N(-1,-4)两点.
(1)求反比例函数和一
次函数的解析式;
(2)根据图象写出反比
例函数的值大于一
次函数的值的x的取
值范围.
综合运用:
M(2,m)
2
0
-1
N(-1,-4)
y
x
综合运用:
M(2,m)
2
0
-1
N(-1,-4)
y
x
(1)求反比例函数和一次函数的解析式;
解:(1)∵点N(-1,-4)在反比例函数图象上
∴k=4,
又∵点M(2,m)在反比例函数
图象上
∴m=2 ∴M(2,2)
∵点M、N都在y=ax+b的图象上
∴y= 2x-2
∴
∴
解得
综合运用:
y
x
2
0
-1
N(-1,-4)
M(2,m)
(2)根据图象写出反比例函数的值大于一次函数的值的x的取值范围.
(2)观察图象得:
当x<-1或0
综合运用:
2.某商场出售一批进价为2元的贺卡,在市场营销中发现此商品的日销售单价x(元)与日销售量y(个)之间有如下关系:
x (元) 3 4 5 6 ……
y(个) 20 15 12 10 ……
(1)猜想并确定在赢利的条件下y与x之间的函数关系式。
(2)设经营此贺卡的销售利润为w元,试求出w与x之间的函数关系式,若物价局规定此贺卡的销售价最高不能超过10元,请你求出当销售单价x定为多少时,才能使获利最大?
……
