沪科版数学九年级上册 22相似三角形的复习课——一线三角模型的应用教案
文档属性
| 名称 | 沪科版数学九年级上册 22相似三角形的复习课——一线三角模型的应用教案 |

|
|
| 格式 | docx | ||
| 文件大小 | 114.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-12-27 20:43:55 | ||
图片预览

文档简介
教学目标:
用“一线三等角”基本模型解决相似三角形中的相关问题;
教学重点.难点:
1.掌握“一线三等角”基本模型;
2.“一线三等角”基本图形的提炼、变式和运用。
课 型:
复习课
教学准备:
PPT
教学过程:
一.例题引入:
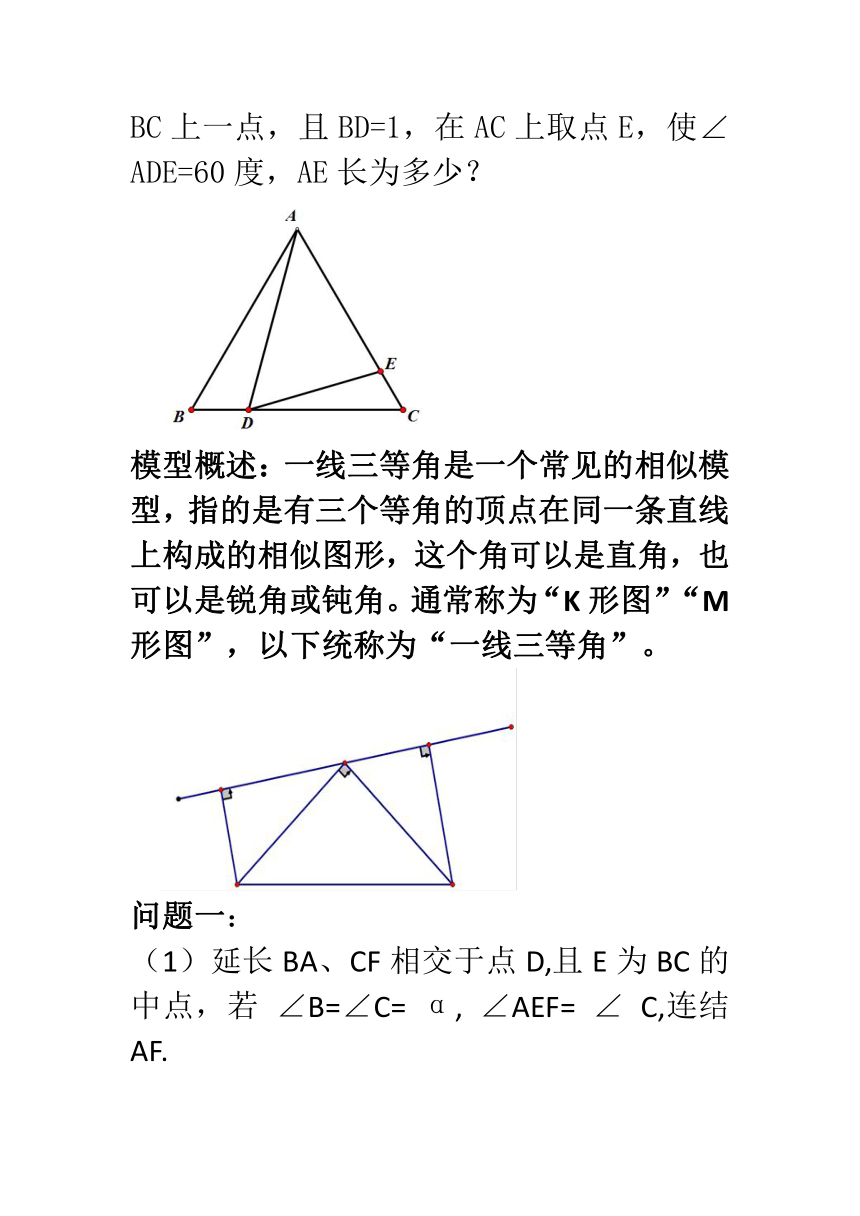
如图,等边△ABC的边长为3,点D是BC上一点,且BD=1,在AC上取点E,使∠ADE=60度,AE长为多少?
模型概述:一线三等角是一个常见的相似模型,指的是有三个等角的顶点在同一条直线上构成的相似图形,这个角可以是直角,也可以是锐角或钝角。通常称为“K形图”“M形图”,以下统称为“一线三等角”。
问题一:
(1)延长BA、CF相交于点D,且E为BC的中点,若 ∠B=∠C= α, ∠AEF= ∠ C,连结AF.
①找出图中的相似三角形
②说出图中相等的角及边之间的关系
(2)延长BA、CF相交于点D,且E为BC的中点,若 ∠B=∠C= α, ∠AEF= ∠ C, 当∠AEF旋转到如图位置时,上述关系还成立吗?
例题讲解:
例1.在矩形ABCD中,AB=4,BC=5,AF平分∠DAE,EF⊥AE,
则CF =
2、如图,四边形ABCD中,AD∥BC,AB=DC=AD=6,∠ABC=70°,点E.F分别在线段AD,DC上,且∠BEF=110°,若AE=3,
DF长为________.
3.如图,正方形ABCD边长为8,M、N分别是BC、CD上的两个动点,当M点在BC上运动时,保持AM和MN垂直.
(1)证明:Rt△ABM∽Rt△MCN;
(2)设BM=x,四边形ABCN的面积为y,求y与x之间的函 数关系式;当M点运动到什么位置时,四边形ABCN的面积最大,并求出最大面积;
(3)当M点运动到什么位置时,
Rt△ABM∽Rt△AMN?
求此时x的值
规律总结:
一线三等角,左右两相似
一线三等角,中点三相似
通过构造基本图形证相似是辅助线添加的重要方法之一.
四.课后练习:
如图,在△ABC 中,∠BAC=135°,
AC = AB, AD⊥AC 交 BC 于点 D,若 AD =AB ,求△ABC的面积
五.板书设计:
一线三等角,左右两相似
一线三等角,中点三相似
通过构造基本图形证相似是辅助线添加的重要方法之一.
六.课后反思:
用“一线三等角”基本模型解决相似三角形中的相关问题;
教学重点.难点:
1.掌握“一线三等角”基本模型;
2.“一线三等角”基本图形的提炼、变式和运用。
课 型:
复习课
教学准备:
PPT
教学过程:
一.例题引入:
如图,等边△ABC的边长为3,点D是BC上一点,且BD=1,在AC上取点E,使∠ADE=60度,AE长为多少?
模型概述:一线三等角是一个常见的相似模型,指的是有三个等角的顶点在同一条直线上构成的相似图形,这个角可以是直角,也可以是锐角或钝角。通常称为“K形图”“M形图”,以下统称为“一线三等角”。
问题一:
(1)延长BA、CF相交于点D,且E为BC的中点,若 ∠B=∠C= α, ∠AEF= ∠ C,连结AF.
①找出图中的相似三角形
②说出图中相等的角及边之间的关系
(2)延长BA、CF相交于点D,且E为BC的中点,若 ∠B=∠C= α, ∠AEF= ∠ C, 当∠AEF旋转到如图位置时,上述关系还成立吗?
例题讲解:
例1.在矩形ABCD中,AB=4,BC=5,AF平分∠DAE,EF⊥AE,
则CF =
2、如图,四边形ABCD中,AD∥BC,AB=DC=AD=6,∠ABC=70°,点E.F分别在线段AD,DC上,且∠BEF=110°,若AE=3,
DF长为________.
3.如图,正方形ABCD边长为8,M、N分别是BC、CD上的两个动点,当M点在BC上运动时,保持AM和MN垂直.
(1)证明:Rt△ABM∽Rt△MCN;
(2)设BM=x,四边形ABCN的面积为y,求y与x之间的函 数关系式;当M点运动到什么位置时,四边形ABCN的面积最大,并求出最大面积;
(3)当M点运动到什么位置时,
Rt△ABM∽Rt△AMN?
求此时x的值
规律总结:
一线三等角,左右两相似
一线三等角,中点三相似
通过构造基本图形证相似是辅助线添加的重要方法之一.
四.课后练习:
如图,在△ABC 中,∠BAC=135°,
AC = AB, AD⊥AC 交 BC 于点 D,若 AD =AB ,求△ABC的面积
五.板书设计:
一线三等角,左右两相似
一线三等角,中点三相似
通过构造基本图形证相似是辅助线添加的重要方法之一.
六.课后反思:
