2021--2022学年北师大版八年级数学上册7.5.1三角形内角和定理课件(共16张PPT)
文档属性
| 名称 | 2021--2022学年北师大版八年级数学上册7.5.1三角形内角和定理课件(共16张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 594.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-12-27 18:25:38 | ||
图片预览




文档简介
(共16张PPT)
第七章 平行线的证明
7.5.1 三角形内角和定理
学习目标
2.会运用三角形内角和定理进行计算.(难点)
1.会用平行线的性质与平角的定义证明三角形内角和等于180°.(重点)
情景导入
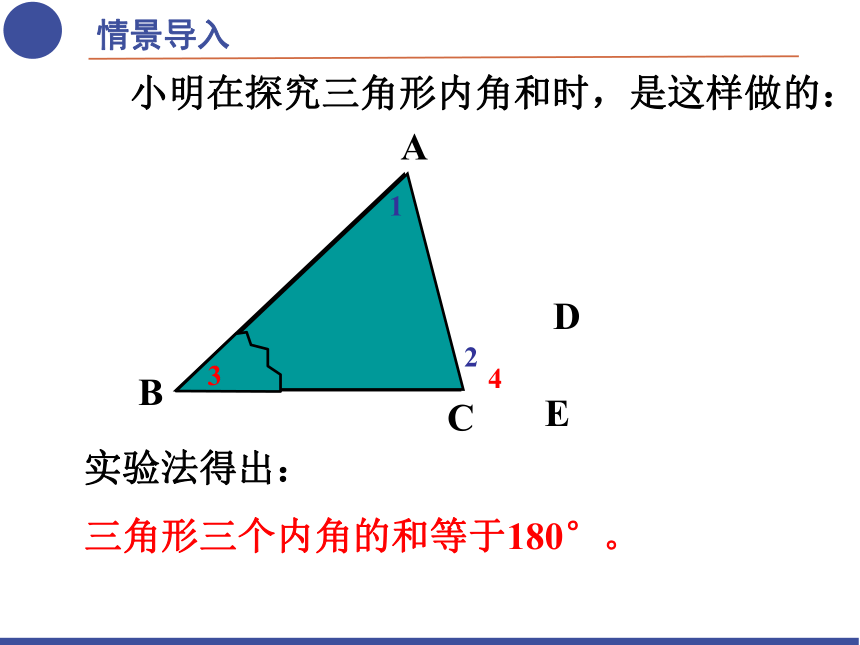
小明在探究三角形内角和时,是这样做的:
A
B
C
3
4
1
2
D
E
实验法得出:
三角形三个内角的和等于180°。
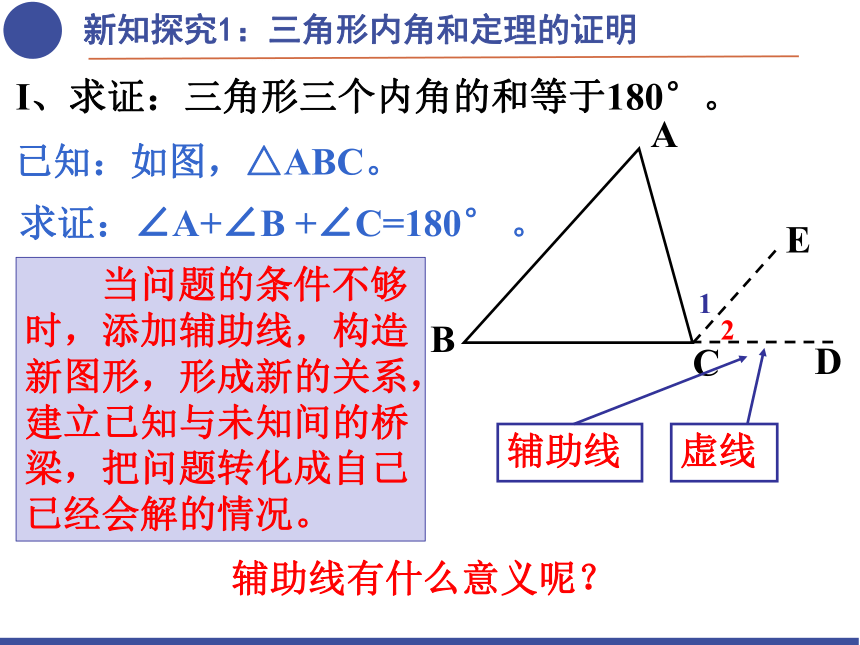
Ⅰ、求证:三角形三个内角的和等于180°。
已知:如图,△ABC。
求证:∠A+∠B +∠C=180° 。
A
B
C
D
E
辅助线
辅助线有什么意义呢?
虚线
1
2
当问题的条件不够时,添加辅助线,构造新图形,形成新的关系,建立已知与未知间的桥梁,把问题转化成自己已经会解的情况。
新知探究1:三角形内角和定理的证明
Ⅰ、求证:三角形三个内角的和等于180°。
已知:如图,△ABC。
求证:∠A+∠B +∠C=180° 。
证明:
∴∠A=∠1
(两直线平行,内错角相等)
延长BC至D,过点
C作CE∥BA。
∵∠1+∠2+ ∠ACB=180°
(平角的定义)
∴∠A+∠B +∠ACB=180°
(等量代换)
A
B
C
∠B=∠2
(两直线平行,同位角相等)
D
E
1
2
新知探究1:三角形内角和定理的证明
新知
三角形内角和定理:
三角形三个内角的和等于180°。
新知探究1:三角形内角和定理的证明
C
A
B
1
2
3
4
5
l
A
C
B
1
2
3
4
5
l
P
6
m
A
B
C
D
E
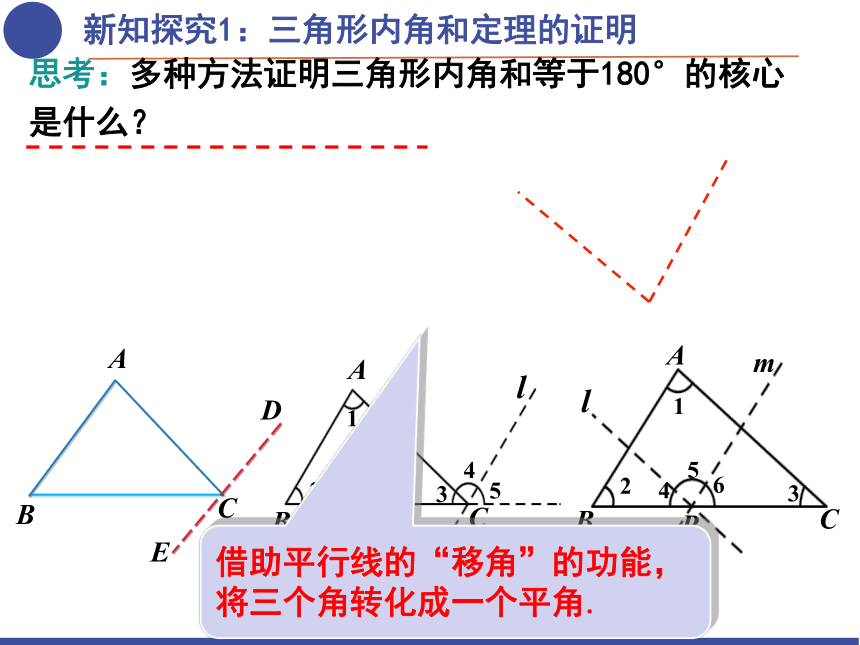
思考:多种方法证明三角形内角和等于180°的核心是什么?
借助平行线的“移角”的功能,将三个角转化成一个平角.
知识要点
在这里,为了证明的需要,在原来的图形上添画的线叫做辅助线.在平面几何里,辅助线通常画成虚线.
思路总结
为了证明三个角的和为180°,转化为一个平角或同旁内角互补等,这种转化思想是数学中的常用方法.
作辅助线
A
B
C
D
解:∵∠BAC=40 °, AD是△ABC的角平分线
∴ ∠BAD= ∠BAC=20 °.
∴在△ABD中,
∠ADB=180°-∠B-∠BAD
=180°-75°-20°
=85°.
例1 如图,在△ABC中, ∠BAC=40 °, ∠B=75 °,AD是△ABC的角平分线,求∠ADB的度数.
经典例题
例2 如图,△ABC中,D在BC的延长线上,过D作DE⊥AB于E,交AC于F.已知∠A=30°,∠FCD=80°,求∠D.
解:∵DE⊥AB,∴∠FEA=90°.
∵在△AEF中,∠FEA=90°,∠A=30°,
∴∠AFE=180°-∠FEA-∠A=60°.
又∵∠CFD=∠AFE,
∴∠CFD=60°.
∴在△CDF中,∠CFD=60°,∠FCD=80°,
∠D=180°-∠CFD-∠FCD=40°.
经典例题
当堂检测
②在△ABC中,∠A :∠B:∠C=1:2:3,则△ABC是
_________三角形 .
1、练一练:
①在△ABC中,∠A=35°,∠ B=43 °,则∠ C= .
③在△ABC中, ∠A= ∠B+10°, ∠C= ∠A + 10°, 则 ∠A= , ∠ B= ,∠ C= .
102°
直角
60°
50°
70°
当堂检测
2.求出下列各图中的x值.
x=70
x=60
x=30
x=50
当堂检测
3.如图,则∠1+∠2+∠3+∠4=___________ .
B
A
C
D
4
1
3
2
E
40°
(
280 °
当堂检测
4.如图,四边形ABCD中,点E在BC上,∠A+∠ADE=180°,∠B=78°,∠C=60°,求∠EDC的度数.
解:∵∠A+∠ADE=180°,
∴AB∥DE,
∴∠CED=∠B=78°.
又∵∠C=60°,
∴∠EDC=180°-(∠CED+∠C)
=180°-(78°+60°)
=42°.
当堂检测
5.如图,在△ABC中,BP平分∠ABC,CP平分∠ACB,若∠BAC=60°,求∠BPC的度数.
解:∵△ABC中,∠A=60°,
∴∠ABC+∠ACB=120°.
∵BP平分∠ABC,CP平分∠ACB,
∴∠PBC+∠PCB= (∠ABC+∠ACB)=60°.
∵∠PBC+∠PCB+∠BPC=180°,
∴∠BPC=180°-60°=120°.
三角形的
内角和定理
证明
了解添加辅助线的方法及其目的
内容
三角形内角和等于180 °
课堂小结
第七章 平行线的证明
7.5.1 三角形内角和定理
学习目标
2.会运用三角形内角和定理进行计算.(难点)
1.会用平行线的性质与平角的定义证明三角形内角和等于180°.(重点)
情景导入
小明在探究三角形内角和时,是这样做的:
A
B
C
3
4
1
2
D
E
实验法得出:
三角形三个内角的和等于180°。
Ⅰ、求证:三角形三个内角的和等于180°。
已知:如图,△ABC。
求证:∠A+∠B +∠C=180° 。
A
B
C
D
E
辅助线
辅助线有什么意义呢?
虚线
1
2
当问题的条件不够时,添加辅助线,构造新图形,形成新的关系,建立已知与未知间的桥梁,把问题转化成自己已经会解的情况。
新知探究1:三角形内角和定理的证明
Ⅰ、求证:三角形三个内角的和等于180°。
已知:如图,△ABC。
求证:∠A+∠B +∠C=180° 。
证明:
∴∠A=∠1
(两直线平行,内错角相等)
延长BC至D,过点
C作CE∥BA。
∵∠1+∠2+ ∠ACB=180°
(平角的定义)
∴∠A+∠B +∠ACB=180°
(等量代换)
A
B
C
∠B=∠2
(两直线平行,同位角相等)
D
E
1
2
新知探究1:三角形内角和定理的证明
新知
三角形内角和定理:
三角形三个内角的和等于180°。
新知探究1:三角形内角和定理的证明
C
A
B
1
2
3
4
5
l
A
C
B
1
2
3
4
5
l
P
6
m
A
B
C
D
E
思考:多种方法证明三角形内角和等于180°的核心是什么?
借助平行线的“移角”的功能,将三个角转化成一个平角.
知识要点
在这里,为了证明的需要,在原来的图形上添画的线叫做辅助线.在平面几何里,辅助线通常画成虚线.
思路总结
为了证明三个角的和为180°,转化为一个平角或同旁内角互补等,这种转化思想是数学中的常用方法.
作辅助线
A
B
C
D
解:∵∠BAC=40 °, AD是△ABC的角平分线
∴ ∠BAD= ∠BAC=20 °.
∴在△ABD中,
∠ADB=180°-∠B-∠BAD
=180°-75°-20°
=85°.
例1 如图,在△ABC中, ∠BAC=40 °, ∠B=75 °,AD是△ABC的角平分线,求∠ADB的度数.
经典例题
例2 如图,△ABC中,D在BC的延长线上,过D作DE⊥AB于E,交AC于F.已知∠A=30°,∠FCD=80°,求∠D.
解:∵DE⊥AB,∴∠FEA=90°.
∵在△AEF中,∠FEA=90°,∠A=30°,
∴∠AFE=180°-∠FEA-∠A=60°.
又∵∠CFD=∠AFE,
∴∠CFD=60°.
∴在△CDF中,∠CFD=60°,∠FCD=80°,
∠D=180°-∠CFD-∠FCD=40°.
经典例题
当堂检测
②在△ABC中,∠A :∠B:∠C=1:2:3,则△ABC是
_________三角形 .
1、练一练:
①在△ABC中,∠A=35°,∠ B=43 °,则∠ C= .
③在△ABC中, ∠A= ∠B+10°, ∠C= ∠A + 10°, 则 ∠A= , ∠ B= ,∠ C= .
102°
直角
60°
50°
70°
当堂检测
2.求出下列各图中的x值.
x=70
x=60
x=30
x=50
当堂检测
3.如图,则∠1+∠2+∠3+∠4=___________ .
B
A
C
D
4
1
3
2
E
40°
(
280 °
当堂检测
4.如图,四边形ABCD中,点E在BC上,∠A+∠ADE=180°,∠B=78°,∠C=60°,求∠EDC的度数.
解:∵∠A+∠ADE=180°,
∴AB∥DE,
∴∠CED=∠B=78°.
又∵∠C=60°,
∴∠EDC=180°-(∠CED+∠C)
=180°-(78°+60°)
=42°.
当堂检测
5.如图,在△ABC中,BP平分∠ABC,CP平分∠ACB,若∠BAC=60°,求∠BPC的度数.
解:∵△ABC中,∠A=60°,
∴∠ABC+∠ACB=120°.
∵BP平分∠ABC,CP平分∠ACB,
∴∠PBC+∠PCB= (∠ABC+∠ACB)=60°.
∵∠PBC+∠PCB+∠BPC=180°,
∴∠BPC=180°-60°=120°.
三角形的
内角和定理
证明
了解添加辅助线的方法及其目的
内容
三角形内角和等于180 °
课堂小结
同课章节目录
- 第一章 勾股定理
- 1 探索勾股定理
- 2 一定是直角三角形吗
- 3 勾股定理的应用
- 第二章 实数
- 1 认识无理数
- 2 平方根
- 3 立方根
- 4 估算
- 5 用计算器开方
- 6 实数
- 7 二次根式
- 第三章 位置与坐标
- 1 确定位置
- 2 平面直角坐标系
- 3 轴对称与坐标变化
- 第四章 一次函数
- 1 函数
- 2 一次函数与正比例函数
- 3 一次函数的图象
- 4 一次函数的应用
- 第五章 二元一次方程组
- 1 认识二元一次方程组
- 2 求解二元一次方程组
- 3 应用二元一次方程组——鸡免同笼
- 4 应用二元一次方程组——增收节支
- 5 应用二元一次方程组——里程碑上的数
- 6 二元一次方程与一次函数
- 7 用二元一次方程组确定一次函数表达式
- 8*三元一次方程组
- 第六章 数据的分析
- 1 平均数
- 2 中位数与众数
- 3 从统计图分析数据的集中趋势
- 4 数据的离散程度
- 第七章 平行线的证明
- 1 为什么要证明
- 2 定义与命题
- 3 平行线的判定
- 4 平行线的性质
- 5 三角形的内角和定理
