沪科版数学八年级上册 13.2 命题的证明 课件(共18张PPT)
文档属性
| 名称 | 沪科版数学八年级上册 13.2 命题的证明 课件(共18张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 114.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-12-27 18:30:28 | ||
图片预览



文档简介
(共18张PPT)
命题的证明
A
B
C
前面我们已经学习了三角形的内角,现在老师给出一个三角形,请同学们 找出它的内角是什么?
A
B
C
D
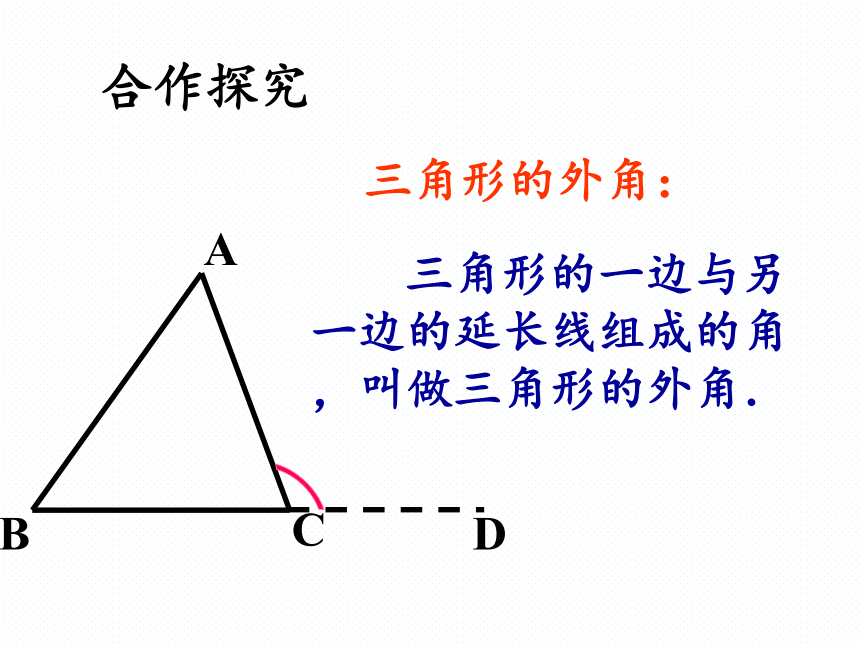
三角形的外角:
三角形的一边与另一边的延长线组成的角,叫做三角形的外角.
合作探究
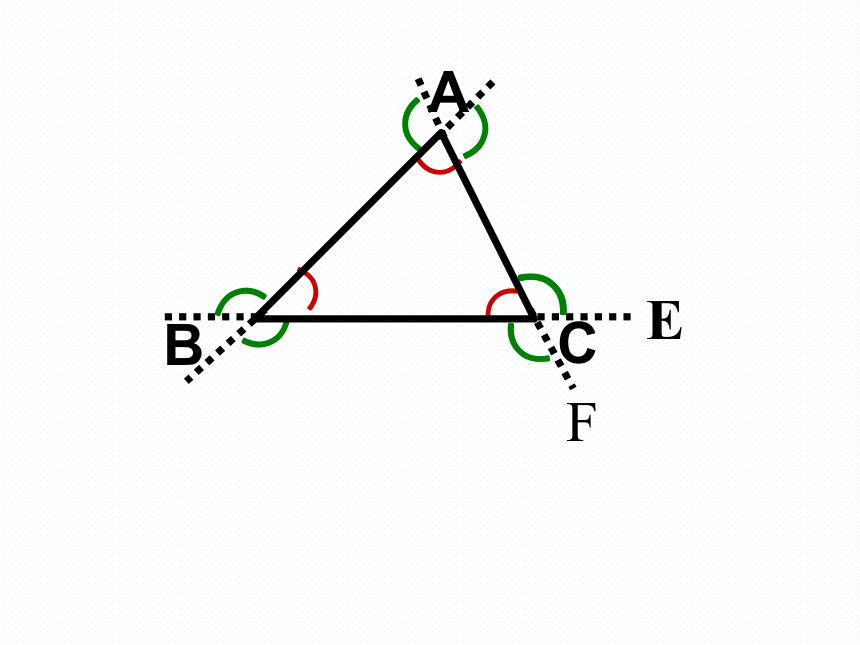
请同学们思考:外角有哪些特点?
1、顶点是三角形的一个顶点
2、一边是三角形一条边
3、另一边是三角形某条边的延长线
)
)
)
)
)
)
)
)
)
A
B
C
E
F
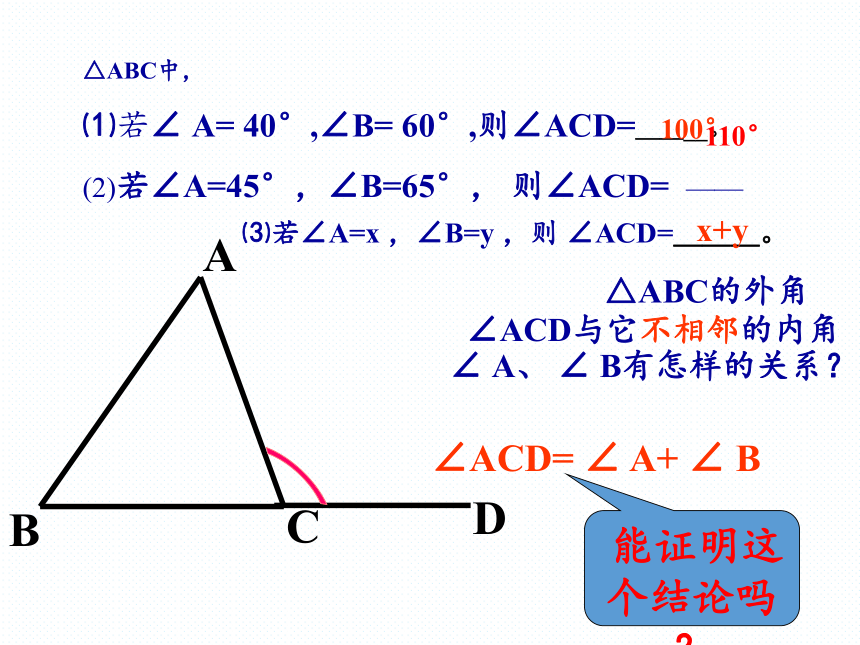
⑶若∠A=x ,∠B=y ,则 ∠ACD=___。
A
B
C
△ABC的外角∠ACD与它不相邻的内角∠ A、 ∠ B有怎样的关系?
D
△ABC中,
⑴若∠ A= 40°,∠B= 60°,则∠ACD=____。
∠ACD= ∠ A+ ∠ B
100°
x+y
能证明这个结论吗?
(2)若∠A=45°,∠B=65°, 则∠ACD= ——
110°
A
B
C
D
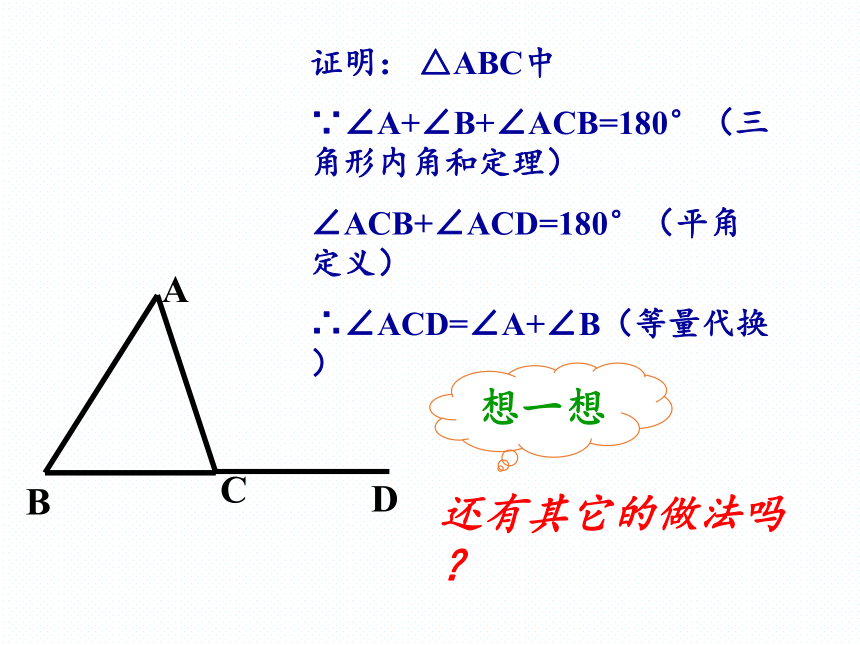
证明: △ABC中
∵∠A+∠B+∠ACB=180°(三角形内角和定理)
∠ACB+∠ACD=180°(平角定义)
∴∠ACD=∠A+∠B(等量代换)
想一想
还有其它的做法吗?
推论1:三角形的一个外角等于与它不相邻 的两个内角的和。
A
C
B
∠ACD ∠A (<、>);
∠ACD ∠B (<、>)
你选谁 ?
D
>
>
推论1:三角形的一个外角等于与 它不相邻 的两个内角的和。
推论2:三角形的一个外角大于与 它不相邻的任何一个内角。
1
60°
110°
求下列各图中∠1的度数。
50°
45°
1
35°
120°
1
当堂训练
2
3
2
1
A
B
C
已知:如图,∠1、∠2、∠3是
△ABC的三个外角
求证: ∠1+∠2+∠3=360°
证明:∵ ∠1=∠ABC+∠ACB
∠2=∠ACB+∠BAC
∠3=∠ABC+∠BAC
(三角形的一个外角等于与它不相邻的两个内角的和)
∴ ∠1+∠2+∠3=2 (∠ABC+∠ACB+∠BAC)
(等式的基本性质)
∵ ∠ABC+∠ACB+∠BAC=180°(三角形内角和定理)
∴ ∠1+∠2+∠3=360°
把图中∠1、 ∠2、 ∠3按从大到小的顺序排列,并说明理由。
解:∠1> ∠2> ∠3
3
2
1
A
B
C
D
E
1
2
3
B
A
C
P
N
M
D
E
F
挑战一下!
∠A+∠B+∠C+∠D+∠E+∠F=____。
360°
总结提升
告诉同学们你本节课的收获是什么?
布置作业
课堂作业:习题13.2第4题,第9题.
家庭作业:1、基础训练13.2(4)
2、预学下一节内容。
谢 谢
命题的证明
A
B
C
前面我们已经学习了三角形的内角,现在老师给出一个三角形,请同学们 找出它的内角是什么?
A
B
C
D
三角形的外角:
三角形的一边与另一边的延长线组成的角,叫做三角形的外角.
合作探究
请同学们思考:外角有哪些特点?
1、顶点是三角形的一个顶点
2、一边是三角形一条边
3、另一边是三角形某条边的延长线
)
)
)
)
)
)
)
)
)
A
B
C
E
F
⑶若∠A=x ,∠B=y ,则 ∠ACD=___。
A
B
C
△ABC的外角∠ACD与它不相邻的内角∠ A、 ∠ B有怎样的关系?
D
△ABC中,
⑴若∠ A= 40°,∠B= 60°,则∠ACD=____。
∠ACD= ∠ A+ ∠ B
100°
x+y
能证明这个结论吗?
(2)若∠A=45°,∠B=65°, 则∠ACD= ——
110°
A
B
C
D
证明: △ABC中
∵∠A+∠B+∠ACB=180°(三角形内角和定理)
∠ACB+∠ACD=180°(平角定义)
∴∠ACD=∠A+∠B(等量代换)
想一想
还有其它的做法吗?
推论1:三角形的一个外角等于与它不相邻 的两个内角的和。
A
C
B
∠ACD ∠A (<、>);
∠ACD ∠B (<、>)
你选谁 ?
D
>
>
推论1:三角形的一个外角等于与 它不相邻 的两个内角的和。
推论2:三角形的一个外角大于与 它不相邻的任何一个内角。
1
60°
110°
求下列各图中∠1的度数。
50°
45°
1
35°
120°
1
当堂训练
2
3
2
1
A
B
C
已知:如图,∠1、∠2、∠3是
△ABC的三个外角
求证: ∠1+∠2+∠3=360°
证明:∵ ∠1=∠ABC+∠ACB
∠2=∠ACB+∠BAC
∠3=∠ABC+∠BAC
(三角形的一个外角等于与它不相邻的两个内角的和)
∴ ∠1+∠2+∠3=2 (∠ABC+∠ACB+∠BAC)
(等式的基本性质)
∵ ∠ABC+∠ACB+∠BAC=180°(三角形内角和定理)
∴ ∠1+∠2+∠3=360°
把图中∠1、 ∠2、 ∠3按从大到小的顺序排列,并说明理由。
解:∠1> ∠2> ∠3
3
2
1
A
B
C
D
E
1
2
3
B
A
C
P
N
M
D
E
F
挑战一下!
∠A+∠B+∠C+∠D+∠E+∠F=____。
360°
总结提升
告诉同学们你本节课的收获是什么?
布置作业
课堂作业:习题13.2第4题,第9题.
家庭作业:1、基础训练13.2(4)
2、预学下一节内容。
谢 谢
