沪科版数学八年级上册 12.4 综合与实践 一次函数模型的应用(1) 课件(共21张PPT)
文档属性
| 名称 | 沪科版数学八年级上册 12.4 综合与实践 一次函数模型的应用(1) 课件(共21张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 490.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-12-27 00:00:00 | ||
图片预览



文档简介
(共21张PPT)
12.4 综合与实践 一次函数模型的应用
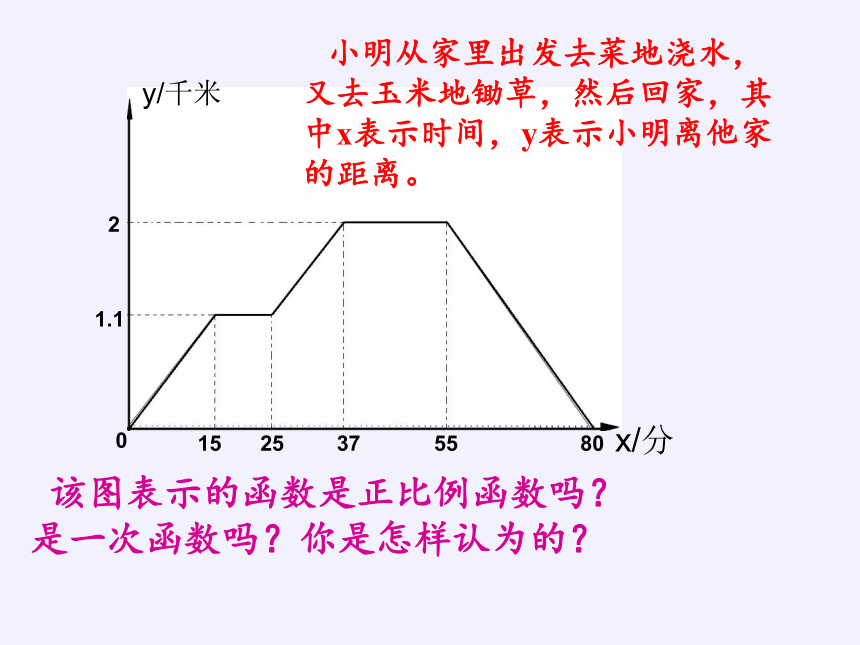
15
25
37
55
80
0
1.1
2
y/千米
x/分
小明从家里出发去菜地浇水,
又去玉米地锄草,然后回家,其
中x表示时间,y表示小明离他家
的距离。
该图表示的函数是正比例函数吗?
是一次函数吗?你是怎样认为的?
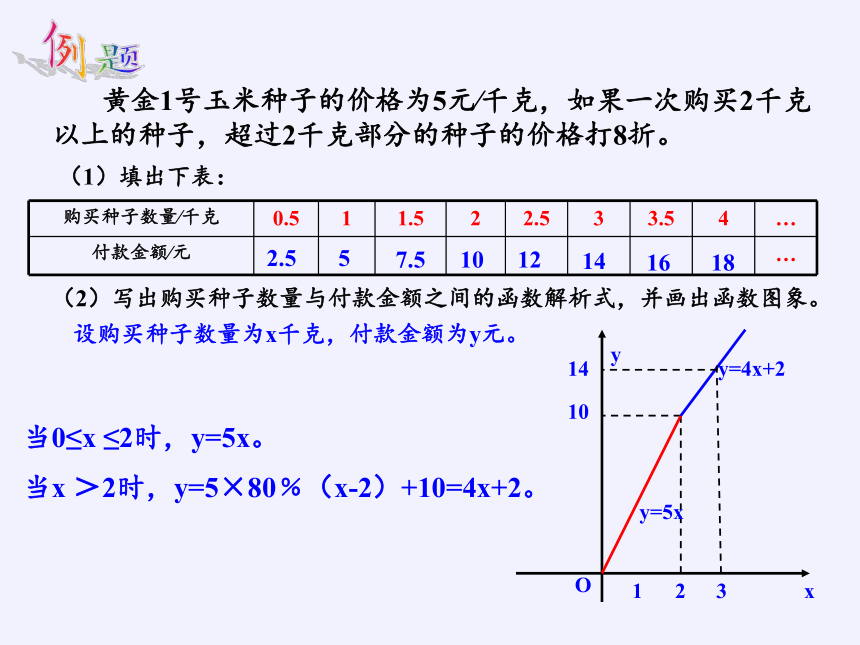
例题
黄金1号玉米种子的价格为5元∕千克,如果一次购买2千克以上的种子,超过2千克部分的种子的价格打8折。
购买种子数量∕千克 0.5 1 1.5 2 2.5 3 3.5 4 …
付款金额∕元 …
2.5
5
7.5
10
12
14
16
18
(1)填出下表:
(2)写出购买种子数量与付款金额之间的函数解析式,并画出函数图象。
设购买种子数量为x千克,付款金额为y元。
当0≤x ≤2时,y=5x。
当x >2时,y=5×80﹪(x-2)+10=4x+2。
O
1
2
y
x
10
y=5x
y=4x+2
14
3
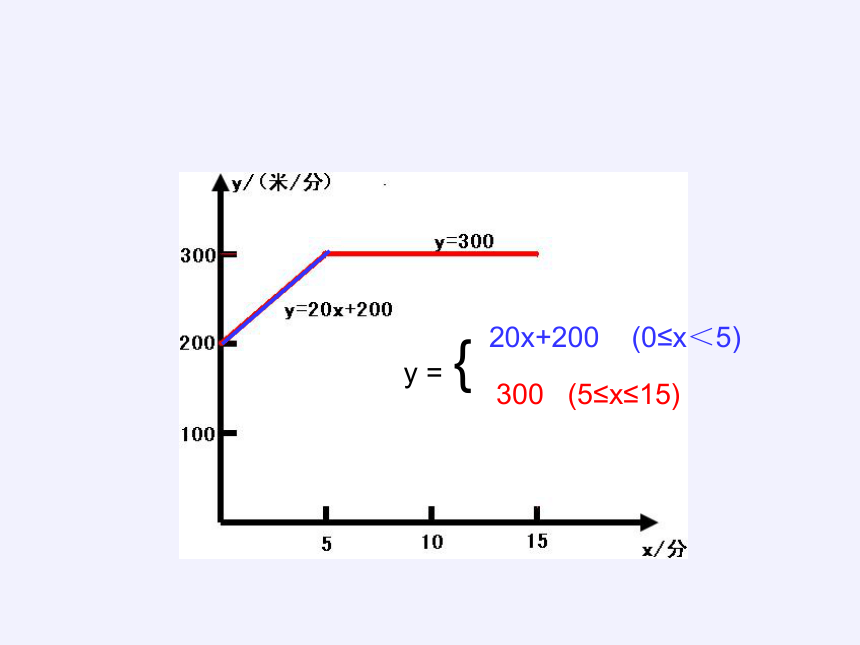
小芳以200米/分钟的速度起跑后,先匀加速跑5分钟,每分钟提高速度20米/分,又匀速跑10分钟,请写出这段时间里她的跑步速度y(米/分钟)随跑步时间x(分钟)变化的函数关系式。
解:跑步的速度 y (米/分)随跑步时间 x (分钟)变化的函数关系式为:
y =
20x+200 (0≤x<5)
300 (5≤x≤15)
{
上述函数,称为分段函数。
y =
20x+200 (0≤x<5)
300 (5≤x≤15)
{
八年级 数学
第十二章 函数
12.2一次函数
分段函数
C
八年级 数学
第十二章 函数
12.2一次函数
分段函数
B
C
D
A
E
F
G
10
11
12
13
14
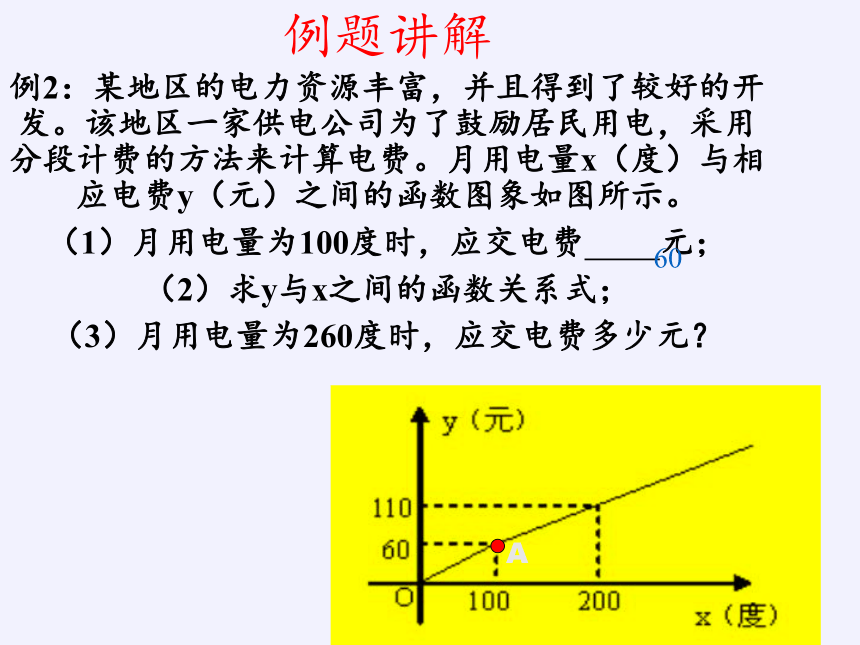
例题讲解
例2:某地区的电力资源丰富,并且得到了较好的开发。该地区一家供电公司为了鼓励居民用电,采用分段计费的方法来计算电费。月用电量x(度)与相应电费y(元)之间的函数图象如图所示。
(1)月用电量为100度时,应交电费 元;
(2)求y与x之间的函数关系式;
(3)月用电量为260度时,应交电费多少元?
A
60
A
B
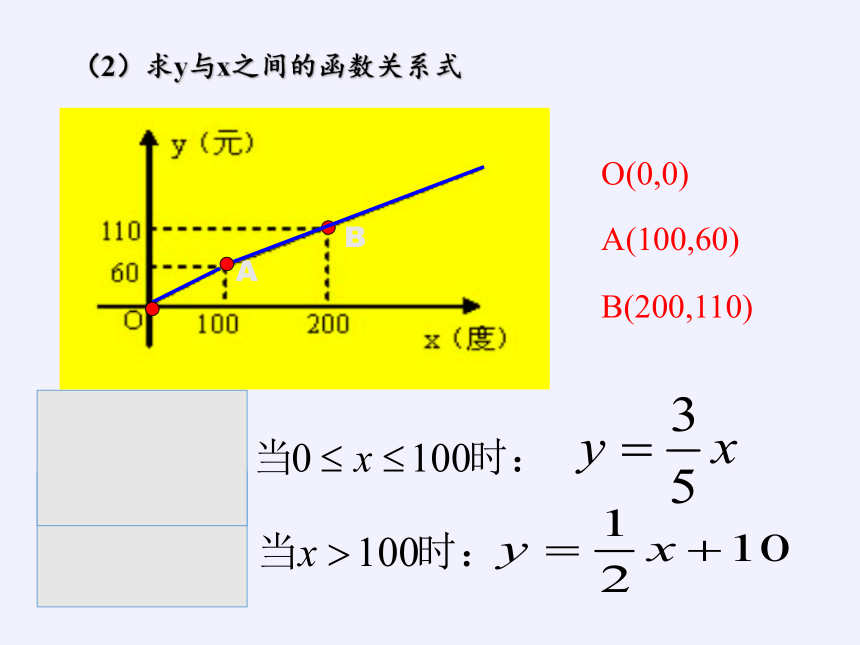
(2)求y与x之间的函数关系式
O(0,0)
A(100,60)
B(200,110)
A
B
(2)求y与x之间的函数关系式
(3)月用电量为260度时,
应交电费多少元?
(1)小明全家在旅游景点游玩了多少小时?
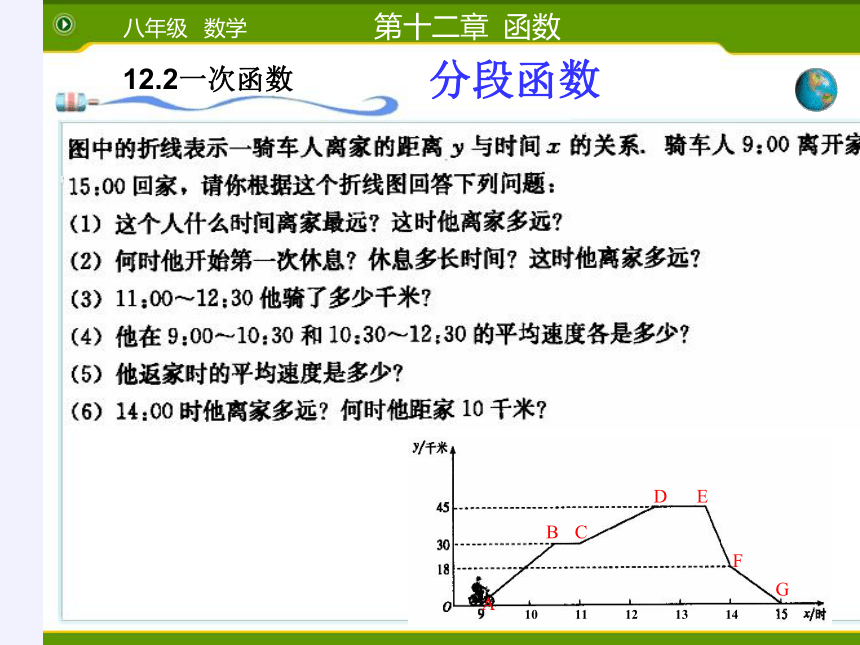
“五一黄金周”的某一 天,小明全家上午8时自驾小汽车从家里出发,到距离180千米的某著名旅游景点游玩。该小汽车离家的距离s(千米)与时间t(时)的关系可以用图中的曲线表示。根据图象提供的有关信息,解答下列问题:
(2)求出返程途中,s(千米)与时间t(时)的函数关系,并回答小明全家到家是什么时间?
(3)若出发时汽车油箱中存油15升,该汽车的油箱总容量为35升,汽车每行驶1千米耗油1/9升。请你就“何时加油和加油量”给小明全家提出一个合理化建议。 (加油所用时间忽略不计)
解:由图像可知,小明全家在旅游 景点游玩了4小时。
解:设s=kx+b,由(14,180)
及(15,120)得
14k+b=180 ①
15k+b=120 ② 解方程组得 k=-60,b=1020。
∴S=-60t+1020 (14≤t≤17)
令S=0,得t=17。
∴返程途中S 与时间t的函数关系是S=-60t+1020,
小明全家当天17:00到家。
(3)本题答案不唯一,只要合理即可,但需注意合理性,
主要体现在:
①9:30前必须加一次油;
②若8:30前将油箱加满,则当天在油用完前的适当时
间必须第二次加油;
③全程可多次加油,但加油总量至少为25升。
议一议
我们周围的还存在哪些分段函数的实例。
如:出租车计费问题,
阶梯水费、电费,
个人所得税,
邮资等等
师生共同小结
一个模型:分段函数
一个方法:数学模型方法
一种数学思想:分类讨论
一种意识:
数学“源于生活、寓于生活、用于生活”
八年级 数学
第十二章 函数
12.2一次函数
课堂小结:
1、分段函数,讨论的方法与一次函数类似。
可分段讨论。
2、较复杂的综合题的解法,先画出草图,
然后根据数形结合,及待定系数求出相应的解
析式
再见!
课堂练习(备选)
1. (如图)某产品的生产流水线每小时可以生产100件产品,生产前没有产品积压,生产3小时后,安排1人装箱,若每小时装产品150件,未装箱的产品数量(Y)是生产时间X的函数,那么,这个函数的大致图象只能是( )。
( A ) ( B ) ( C ) ( D )
A
月份 用水量(m3) 水费(元)
3 5 7.5
4 9 27
课堂练习(备选)
2. 某省是水资源比较贫乏地区之一,为了加强公民的节水和用水意识,合理利用水资源,各地采用价格调控等手段达到节约水的目的。现在某市规定如下用水收费标准:每户每月的用水不超过6立方米时,水费按照每立方米a元收费;超过6立方米时,不超过的部分每立方米仍按a元收费,超过的部分每立方米按c元收费。该市某户今年3、4月份的用水量和水费如下表所示:
月份 用水量(m3) 水费(元)
3 5 7.5
4 9 27
课堂练习(备选)
设某户每月用水量为x(立方米),应交水费为y(元)。
求:(1)a、c的值
(2)并写出用水不超过6立方米和超过6立方米时,y与x之间的函数关系式;
(3)该户5月份的用水量为8立方米,求该户5月份的水费是多少元?
该市某户今年3、4月份的用水量和水费如下表所示:
a=1.5 c=6
Y=1.5x (0≤x≤6)
Y=6x-27 (x>6)
21元
3、近几年来,由于经济和社会发展迅速,用电矛盾越来越突出。为缓解用电紧张,某电力公司特制定了新的用电收费标准,每月用电量x(度)与应付电费y(元)的关系如图所示。
⑴请你根据图像所描述的信息,分别求出当0≤x≤50和x>50时,y与x的函数关系式。
⑵根据你的分析:当每月用电量不超过50度时,收费标准是_______;当每月用电量超过50度时,收费标准是:
Y=0.5x (0≤x≤50)
Y=0.9x-20 (x>50)
不超过50度部分按0.5元/度计算,超过部分按0.9元/度计算。
0.5元/度;
课堂练习(备选)
谢 谢
12.4 综合与实践 一次函数模型的应用
15
25
37
55
80
0
1.1
2
y/千米
x/分
小明从家里出发去菜地浇水,
又去玉米地锄草,然后回家,其
中x表示时间,y表示小明离他家
的距离。
该图表示的函数是正比例函数吗?
是一次函数吗?你是怎样认为的?
例题
黄金1号玉米种子的价格为5元∕千克,如果一次购买2千克以上的种子,超过2千克部分的种子的价格打8折。
购买种子数量∕千克 0.5 1 1.5 2 2.5 3 3.5 4 …
付款金额∕元 …
2.5
5
7.5
10
12
14
16
18
(1)填出下表:
(2)写出购买种子数量与付款金额之间的函数解析式,并画出函数图象。
设购买种子数量为x千克,付款金额为y元。
当0≤x ≤2时,y=5x。
当x >2时,y=5×80﹪(x-2)+10=4x+2。
O
1
2
y
x
10
y=5x
y=4x+2
14
3
小芳以200米/分钟的速度起跑后,先匀加速跑5分钟,每分钟提高速度20米/分,又匀速跑10分钟,请写出这段时间里她的跑步速度y(米/分钟)随跑步时间x(分钟)变化的函数关系式。
解:跑步的速度 y (米/分)随跑步时间 x (分钟)变化的函数关系式为:
y =
20x+200 (0≤x<5)
300 (5≤x≤15)
{
上述函数,称为分段函数。
y =
20x+200 (0≤x<5)
300 (5≤x≤15)
{
八年级 数学
第十二章 函数
12.2一次函数
分段函数
C
八年级 数学
第十二章 函数
12.2一次函数
分段函数
B
C
D
A
E
F
G
10
11
12
13
14
例题讲解
例2:某地区的电力资源丰富,并且得到了较好的开发。该地区一家供电公司为了鼓励居民用电,采用分段计费的方法来计算电费。月用电量x(度)与相应电费y(元)之间的函数图象如图所示。
(1)月用电量为100度时,应交电费 元;
(2)求y与x之间的函数关系式;
(3)月用电量为260度时,应交电费多少元?
A
60
A
B
(2)求y与x之间的函数关系式
O(0,0)
A(100,60)
B(200,110)
A
B
(2)求y与x之间的函数关系式
(3)月用电量为260度时,
应交电费多少元?
(1)小明全家在旅游景点游玩了多少小时?
“五一黄金周”的某一 天,小明全家上午8时自驾小汽车从家里出发,到距离180千米的某著名旅游景点游玩。该小汽车离家的距离s(千米)与时间t(时)的关系可以用图中的曲线表示。根据图象提供的有关信息,解答下列问题:
(2)求出返程途中,s(千米)与时间t(时)的函数关系,并回答小明全家到家是什么时间?
(3)若出发时汽车油箱中存油15升,该汽车的油箱总容量为35升,汽车每行驶1千米耗油1/9升。请你就“何时加油和加油量”给小明全家提出一个合理化建议。 (加油所用时间忽略不计)
解:由图像可知,小明全家在旅游 景点游玩了4小时。
解:设s=kx+b,由(14,180)
及(15,120)得
14k+b=180 ①
15k+b=120 ② 解方程组得 k=-60,b=1020。
∴S=-60t+1020 (14≤t≤17)
令S=0,得t=17。
∴返程途中S 与时间t的函数关系是S=-60t+1020,
小明全家当天17:00到家。
(3)本题答案不唯一,只要合理即可,但需注意合理性,
主要体现在:
①9:30前必须加一次油;
②若8:30前将油箱加满,则当天在油用完前的适当时
间必须第二次加油;
③全程可多次加油,但加油总量至少为25升。
议一议
我们周围的还存在哪些分段函数的实例。
如:出租车计费问题,
阶梯水费、电费,
个人所得税,
邮资等等
师生共同小结
一个模型:分段函数
一个方法:数学模型方法
一种数学思想:分类讨论
一种意识:
数学“源于生活、寓于生活、用于生活”
八年级 数学
第十二章 函数
12.2一次函数
课堂小结:
1、分段函数,讨论的方法与一次函数类似。
可分段讨论。
2、较复杂的综合题的解法,先画出草图,
然后根据数形结合,及待定系数求出相应的解
析式
再见!
课堂练习(备选)
1. (如图)某产品的生产流水线每小时可以生产100件产品,生产前没有产品积压,生产3小时后,安排1人装箱,若每小时装产品150件,未装箱的产品数量(Y)是生产时间X的函数,那么,这个函数的大致图象只能是( )。
( A ) ( B ) ( C ) ( D )
A
月份 用水量(m3) 水费(元)
3 5 7.5
4 9 27
课堂练习(备选)
2. 某省是水资源比较贫乏地区之一,为了加强公民的节水和用水意识,合理利用水资源,各地采用价格调控等手段达到节约水的目的。现在某市规定如下用水收费标准:每户每月的用水不超过6立方米时,水费按照每立方米a元收费;超过6立方米时,不超过的部分每立方米仍按a元收费,超过的部分每立方米按c元收费。该市某户今年3、4月份的用水量和水费如下表所示:
月份 用水量(m3) 水费(元)
3 5 7.5
4 9 27
课堂练习(备选)
设某户每月用水量为x(立方米),应交水费为y(元)。
求:(1)a、c的值
(2)并写出用水不超过6立方米和超过6立方米时,y与x之间的函数关系式;
(3)该户5月份的用水量为8立方米,求该户5月份的水费是多少元?
该市某户今年3、4月份的用水量和水费如下表所示:
a=1.5 c=6
Y=1.5x (0≤x≤6)
Y=6x-27 (x>6)
21元
3、近几年来,由于经济和社会发展迅速,用电矛盾越来越突出。为缓解用电紧张,某电力公司特制定了新的用电收费标准,每月用电量x(度)与应付电费y(元)的关系如图所示。
⑴请你根据图像所描述的信息,分别求出当0≤x≤50和x>50时,y与x的函数关系式。
⑵根据你的分析:当每月用电量不超过50度时,收费标准是_______;当每月用电量超过50度时,收费标准是:
Y=0.5x (0≤x≤50)
Y=0.9x-20 (x>50)
不超过50度部分按0.5元/度计算,超过部分按0.9元/度计算。
0.5元/度;
课堂练习(备选)
谢 谢
