沪科版数学九年级上册 22.4 图形的位似变换(教案)
文档属性
| 名称 | 沪科版数学九年级上册 22.4 图形的位似变换(教案) |

|
|
| 格式 | doc | ||
| 文件大小 | 519.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-12-28 07:09:02 | ||
图片预览

文档简介
图形的位似变换
【教学目标】
1.理解图形的位似概念,掌握位似图形的性质。
2.会利用作位似图形的方法把一个图形进行放大或缩小。
3.经历位似图形性质的探索过程,进一步发展学生的探究、交流能力,培养学生动手、动脑、手脑和谐一致的习惯。
4.利用图形的位似解决一些简单的实际问题,并在此过程中培养学生的数学应用意识。
5.发展学生的合情推理能力和初步的逻辑推理能力。
【教学重点】
图形的位似概念、位似图形的性质及利用位似把一个图形放大或缩小。
【教学难点】
位似图形的画法。
【课时安排】
2课时。
【教学过程】
【第一课时】
一、创设情景,构建新知。
(一)位似图形的概念:
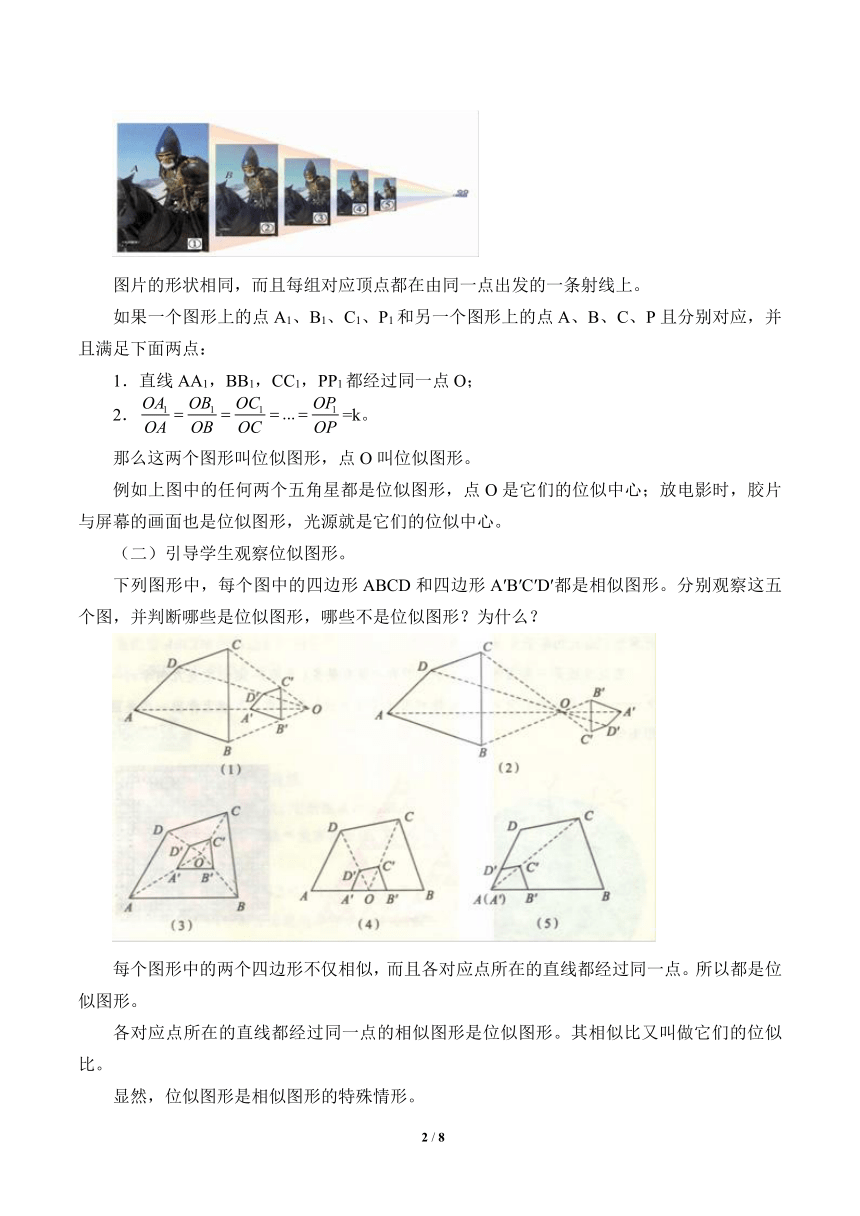
下列两幅图有什么共同特点?通过对图的观察能从生活中找到一种感觉吗?(像一种什么镜头。)
图片的形状相同,而且每组对应顶点都在由同一点出发的一条射线上。
如果一个图形上的点A1、B1、C1、P1和另一个图形上的点A、B、C、P且分别对应,并且满足下面两点:
1.直线AA1,BB1,CC1,PP1都经过同一点O;
2.=k。
那么这两个图形叫位似图形,点O叫位似图形。
例如上图中的任何两个五角星都是位似图形,点O是它们的位似中心;放电影时,胶片与屏幕的画面也是位似图形,光源就是它们的位似中心。
(二)引导学生观察位似图形。
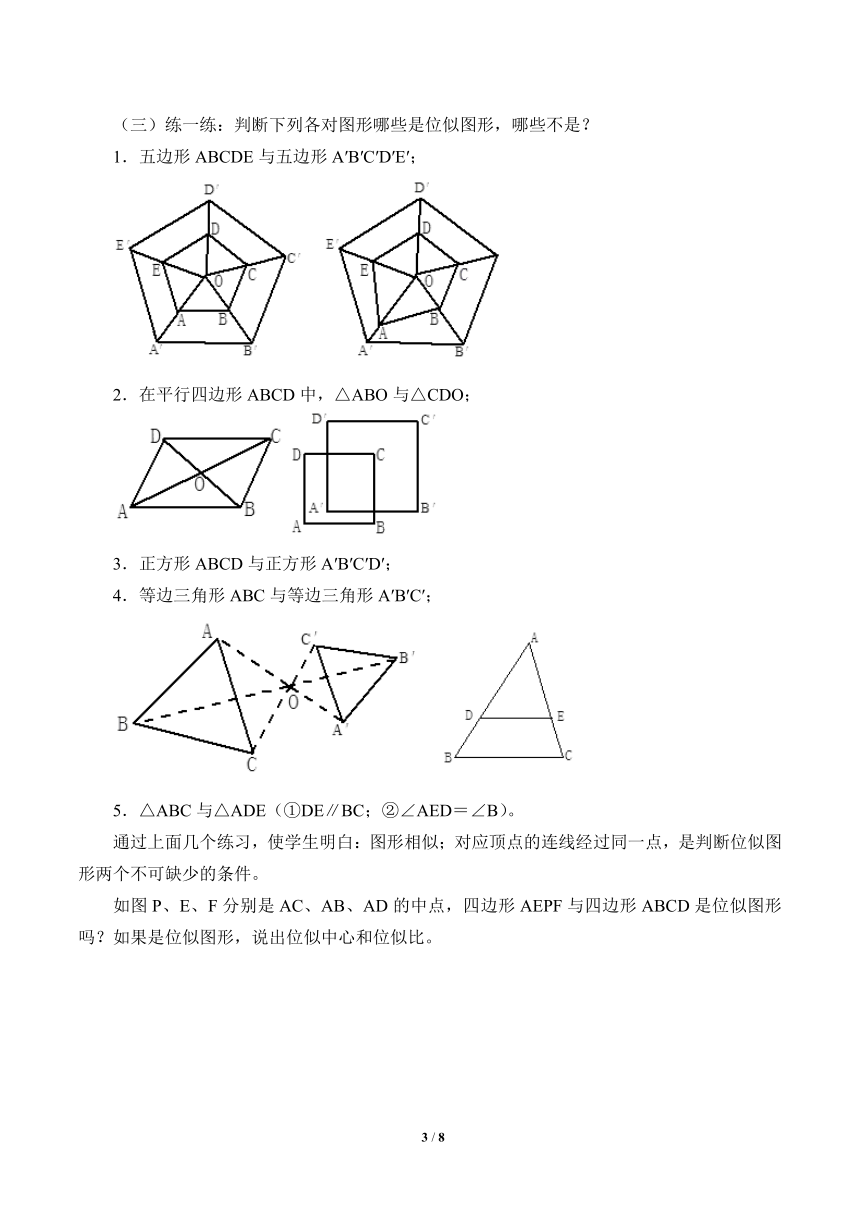
下列图形中,每个图中的四边形ABCD和四边形A′B′C′D′都是相似图形。分别观察这五个图,并判断哪些是位似图形,哪些不是位似图形?为什么?
每个图形中的两个四边形不仅相似,而且各对应点所在的直线都经过同一点。所以都是位似图形。
各对应点所在的直线都经过同一点的相似图形是位似图形。其相似比又叫做它们的位似比。
显然,位似图形是相似图形的特殊情形。
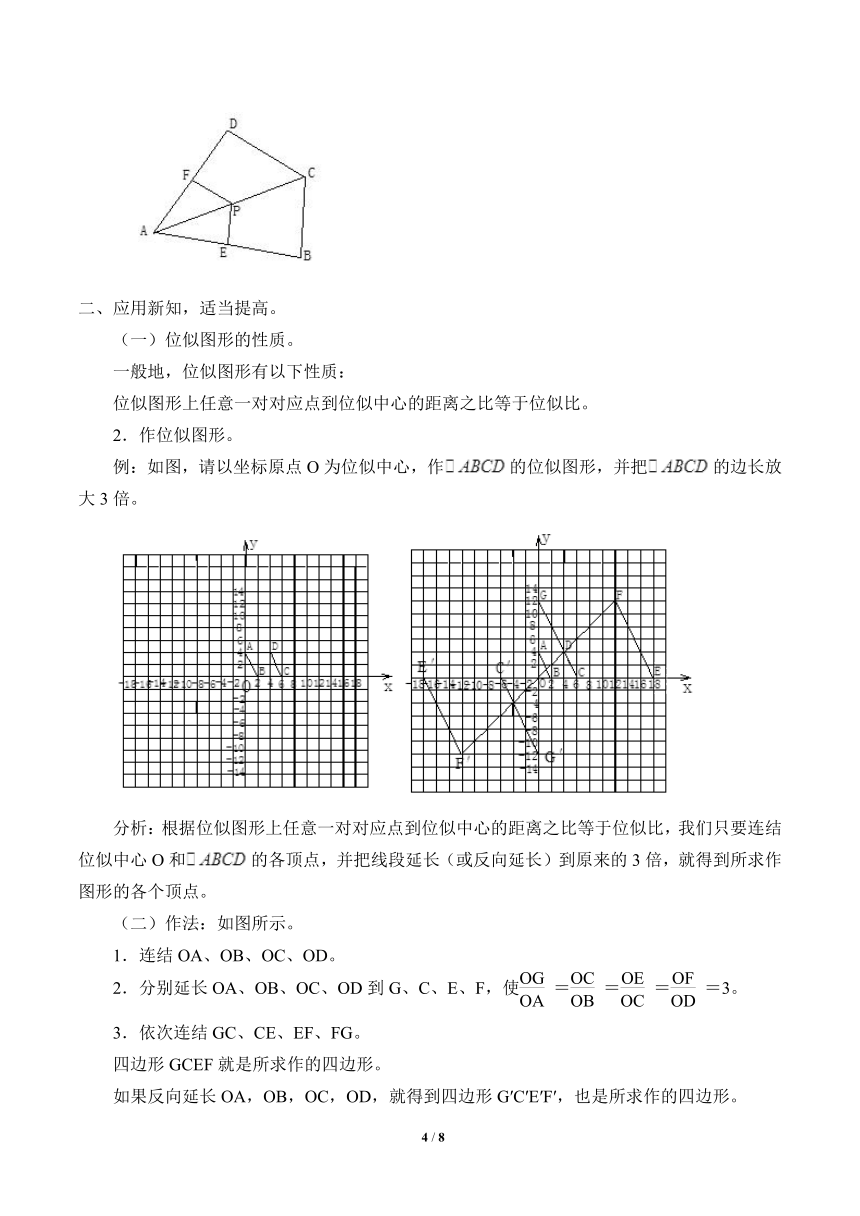
(三)练一练:判断下列各对图形哪些是位似图形,哪些不是?
1.五边形ABCDE与五边形A′B′C′D′E′;
2.在平行四边形ABCD中,△ABO与△CDO;
3.正方形ABCD与正方形A′B′C′D′;
4.等边三角形ABC与等边三角形A′B′C′;
5.△ABC与△ADE(①DE∥BC;②∠AED=∠B)。
通过上面几个练习,使学生明白:图形相似;对应顶点的连线经过同一点,是判断位似图形两个不可缺少的条件。
如图P、E、F分别是AC、AB、AD的中点,四边形AEPF与四边形ABCD是位似图形吗?如果是位似图形,说出位似中心和位似比。
二、应用新知,适当提高。
(一)位似图形的性质。
一般地,位似图形有以下性质:
位似图形上任意一对对应点到位似中心的距离之比等于位似比。
2.作位似图形。
例:如图,请以坐标原点O为位似中心,作的位似图形,并把的边长放大3倍。
分析:根据位似图形上任意一对对应点到位似中心的距离之比等于位似比,我们只要连结位似中心O和的各顶点,并把线段延长(或反向延长)到原来的3倍,就得到所求作图形的各个顶点。
(二)作法:如图所示。
1.连结OA、OB、OC、OD。
2.分别延长OA、OB、OC、OD到G、C、E、F,使====3。
3.依次连结GC、CE、EF、FG。
四边形GCEF就是所求作的四边形。
如果反向延长OA,OB,OC,OD,就得到四边形G′C′E′F′,也是所求作的四边形。
(三)想一想:
1.四边形GCEF与四边形G′C′E′F′具有怎样的对称性?
2.怎样运用像与原像对应点的坐标关系,画出以原点为位似中心的位似图形?
比较图形中各对应点的坐标,我们还不难发现:
以坐标原点为位似中心的位似变换有以下性质:若原图形上点的坐标为(x,y),像与原图形的位似比为k,则像上的对应点的坐标为(kx,ky)或(-kx,-ky)。
练一练:
1.如图,已知△ABC和点O。以O为位似中心,求作△ABC的位似图形,并把△ABC的边长缩小到原来的。
2.如图,在直角坐标系中,△ABC的各个顶点的坐标为A(-1,1),B(2,3),C(0,3)。现要以坐标原点O为位似中心,位似比为,作△ABC的位似图形△A′B′C′,则它的顶点A′、B′、C′的坐标各是多少?
【作业布置】
书上练习题,基础训练同步练习。
【第二课时】
一、回顾与反思。
(一)什么叫相似多边形?
(二)什么叫相似多边形的相似比?
(三)判断两个三角形相似有哪些方法?
二、概念的引入。
展示图片:
上面的一组图片是形状相同的图形,在图片①上取一点A,它与另一图片(如图片②)上的相应点B之间的连线是否经过镜头P的中心?在图片上换其他的点试一试,还有类似的结论吗?
引入概念:
如果两个图形不仅相似,而且每组对应点所在的直线都经过同一个点,那么这样的两个图形叫做位似图形,这个点叫做位似中心,这时的相似比又称为位似比。
练一练:
在下图中,(1),(3)中的两个图形是位似图形,(2)中的两个图形不是位似图形。分别指出图(1),(3)各自的位似中心。
三、探究位似图形的性质。
议一议:
在如图中任取一对对应点,度量这两个点到位似中心的距离,它们的比与位似比有什么关系?
在图(3)中再试一试,还有类似的规律吗?
位似图形的性质:位似图形上的任意一对对应点到位似中心的距离之比等于位似比。
四、应用位似进行图形的缩放:
按如下方法可以将△ABC的三边缩小为原来的1/2:
如图,任取一点O,连接AO、BO、CO,并取它们的中点D、E、F;△DEF的三边就是△ABC相应三边的1/2。实际上△ABC与△DEF是位似图形。
做一做:
任意画一个三角形,用上面的方法亲自试一试。
五、应用举例:
(一)例1:
1.如果在射线OA、OB、OC上分别取D、E、F,使OD=2OA,OE=2OB,OF=2OC,那么,结果又会怎样?
结果会得到一个放大了的△DEF,且△DEF的三边是△ABC三边的2倍。即它们的位似比是2:1。
2.如果在射线AO,BO,CO上分别取点D,E,F使DO=OA,EO=OB,FO=OC,那么,结果又会怎样呢?结果会得到一个与△ABC全等的△DEF。即它们的位似比是1:1。
3.如果在射线AO、BO、CO上分别取点D、E、F使DO=2OA,EO=2OB,FO=2OC,那么,结果又会怎样呢?
(二)例2:如图所示,作出一个新图形,使新图形与原图形对应线段的比是2:1。
【作业布置】
习题22.4的1、2、3。
8 / 8
【教学目标】
1.理解图形的位似概念,掌握位似图形的性质。
2.会利用作位似图形的方法把一个图形进行放大或缩小。
3.经历位似图形性质的探索过程,进一步发展学生的探究、交流能力,培养学生动手、动脑、手脑和谐一致的习惯。
4.利用图形的位似解决一些简单的实际问题,并在此过程中培养学生的数学应用意识。
5.发展学生的合情推理能力和初步的逻辑推理能力。
【教学重点】
图形的位似概念、位似图形的性质及利用位似把一个图形放大或缩小。
【教学难点】
位似图形的画法。
【课时安排】
2课时。
【教学过程】
【第一课时】
一、创设情景,构建新知。
(一)位似图形的概念:
下列两幅图有什么共同特点?通过对图的观察能从生活中找到一种感觉吗?(像一种什么镜头。)
图片的形状相同,而且每组对应顶点都在由同一点出发的一条射线上。
如果一个图形上的点A1、B1、C1、P1和另一个图形上的点A、B、C、P且分别对应,并且满足下面两点:
1.直线AA1,BB1,CC1,PP1都经过同一点O;
2.=k。
那么这两个图形叫位似图形,点O叫位似图形。
例如上图中的任何两个五角星都是位似图形,点O是它们的位似中心;放电影时,胶片与屏幕的画面也是位似图形,光源就是它们的位似中心。
(二)引导学生观察位似图形。
下列图形中,每个图中的四边形ABCD和四边形A′B′C′D′都是相似图形。分别观察这五个图,并判断哪些是位似图形,哪些不是位似图形?为什么?
每个图形中的两个四边形不仅相似,而且各对应点所在的直线都经过同一点。所以都是位似图形。
各对应点所在的直线都经过同一点的相似图形是位似图形。其相似比又叫做它们的位似比。
显然,位似图形是相似图形的特殊情形。
(三)练一练:判断下列各对图形哪些是位似图形,哪些不是?
1.五边形ABCDE与五边形A′B′C′D′E′;
2.在平行四边形ABCD中,△ABO与△CDO;
3.正方形ABCD与正方形A′B′C′D′;
4.等边三角形ABC与等边三角形A′B′C′;
5.△ABC与△ADE(①DE∥BC;②∠AED=∠B)。
通过上面几个练习,使学生明白:图形相似;对应顶点的连线经过同一点,是判断位似图形两个不可缺少的条件。
如图P、E、F分别是AC、AB、AD的中点,四边形AEPF与四边形ABCD是位似图形吗?如果是位似图形,说出位似中心和位似比。
二、应用新知,适当提高。
(一)位似图形的性质。
一般地,位似图形有以下性质:
位似图形上任意一对对应点到位似中心的距离之比等于位似比。
2.作位似图形。
例:如图,请以坐标原点O为位似中心,作的位似图形,并把的边长放大3倍。
分析:根据位似图形上任意一对对应点到位似中心的距离之比等于位似比,我们只要连结位似中心O和的各顶点,并把线段延长(或反向延长)到原来的3倍,就得到所求作图形的各个顶点。
(二)作法:如图所示。
1.连结OA、OB、OC、OD。
2.分别延长OA、OB、OC、OD到G、C、E、F,使====3。
3.依次连结GC、CE、EF、FG。
四边形GCEF就是所求作的四边形。
如果反向延长OA,OB,OC,OD,就得到四边形G′C′E′F′,也是所求作的四边形。
(三)想一想:
1.四边形GCEF与四边形G′C′E′F′具有怎样的对称性?
2.怎样运用像与原像对应点的坐标关系,画出以原点为位似中心的位似图形?
比较图形中各对应点的坐标,我们还不难发现:
以坐标原点为位似中心的位似变换有以下性质:若原图形上点的坐标为(x,y),像与原图形的位似比为k,则像上的对应点的坐标为(kx,ky)或(-kx,-ky)。
练一练:
1.如图,已知△ABC和点O。以O为位似中心,求作△ABC的位似图形,并把△ABC的边长缩小到原来的。
2.如图,在直角坐标系中,△ABC的各个顶点的坐标为A(-1,1),B(2,3),C(0,3)。现要以坐标原点O为位似中心,位似比为,作△ABC的位似图形△A′B′C′,则它的顶点A′、B′、C′的坐标各是多少?
【作业布置】
书上练习题,基础训练同步练习。
【第二课时】
一、回顾与反思。
(一)什么叫相似多边形?
(二)什么叫相似多边形的相似比?
(三)判断两个三角形相似有哪些方法?
二、概念的引入。
展示图片:
上面的一组图片是形状相同的图形,在图片①上取一点A,它与另一图片(如图片②)上的相应点B之间的连线是否经过镜头P的中心?在图片上换其他的点试一试,还有类似的结论吗?
引入概念:
如果两个图形不仅相似,而且每组对应点所在的直线都经过同一个点,那么这样的两个图形叫做位似图形,这个点叫做位似中心,这时的相似比又称为位似比。
练一练:
在下图中,(1),(3)中的两个图形是位似图形,(2)中的两个图形不是位似图形。分别指出图(1),(3)各自的位似中心。
三、探究位似图形的性质。
议一议:
在如图中任取一对对应点,度量这两个点到位似中心的距离,它们的比与位似比有什么关系?
在图(3)中再试一试,还有类似的规律吗?
位似图形的性质:位似图形上的任意一对对应点到位似中心的距离之比等于位似比。
四、应用位似进行图形的缩放:
按如下方法可以将△ABC的三边缩小为原来的1/2:
如图,任取一点O,连接AO、BO、CO,并取它们的中点D、E、F;△DEF的三边就是△ABC相应三边的1/2。实际上△ABC与△DEF是位似图形。
做一做:
任意画一个三角形,用上面的方法亲自试一试。
五、应用举例:
(一)例1:
1.如果在射线OA、OB、OC上分别取D、E、F,使OD=2OA,OE=2OB,OF=2OC,那么,结果又会怎样?
结果会得到一个放大了的△DEF,且△DEF的三边是△ABC三边的2倍。即它们的位似比是2:1。
2.如果在射线AO,BO,CO上分别取点D,E,F使DO=OA,EO=OB,FO=OC,那么,结果又会怎样呢?结果会得到一个与△ABC全等的△DEF。即它们的位似比是1:1。
3.如果在射线AO、BO、CO上分别取点D、E、F使DO=2OA,EO=2OB,FO=2OC,那么,结果又会怎样呢?
(二)例2:如图所示,作出一个新图形,使新图形与原图形对应线段的比是2:1。
【作业布置】
习题22.4的1、2、3。
8 / 8
