沪科版数学九年级上册 22.3 相似三角形的性质教案
文档属性
| 名称 | 沪科版数学九年级上册 22.3 相似三角形的性质教案 |
|
|
| 格式 | docx | ||
| 文件大小 | 53.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-12-28 07:14:32 | ||
图片预览

文档简介
22.3相似三角形的性质
教学目标:
1、掌握相似三角形的性质定理1的内容及证明,使学生进一步理解相似三角形的概念和判定。
2、能运用相似三角形的性质定理1来解决有关问题。
3、通过与“全等三角形的对应线段相等”进行类比,渗透类比的数学思想
4、经历性质的探索过程,进一步提高学生探究、交流能力,培养学生合情推理能力和初步逻辑推理意识。
教学重点:理解相似三角形的性质定理l并能初步运用
教学难点:相似三角形的性质定理l的证明
教学准备:多媒体课件
教学过程:
回顾与思考
1、两三角形相似,他们的对应角和对应边有什么关系?
2、三角形有哪些主要线段?在全等三角形中这些对应线段有什么关系?
猜想:在相似三角形中这些对应线段会有怎样的关系?
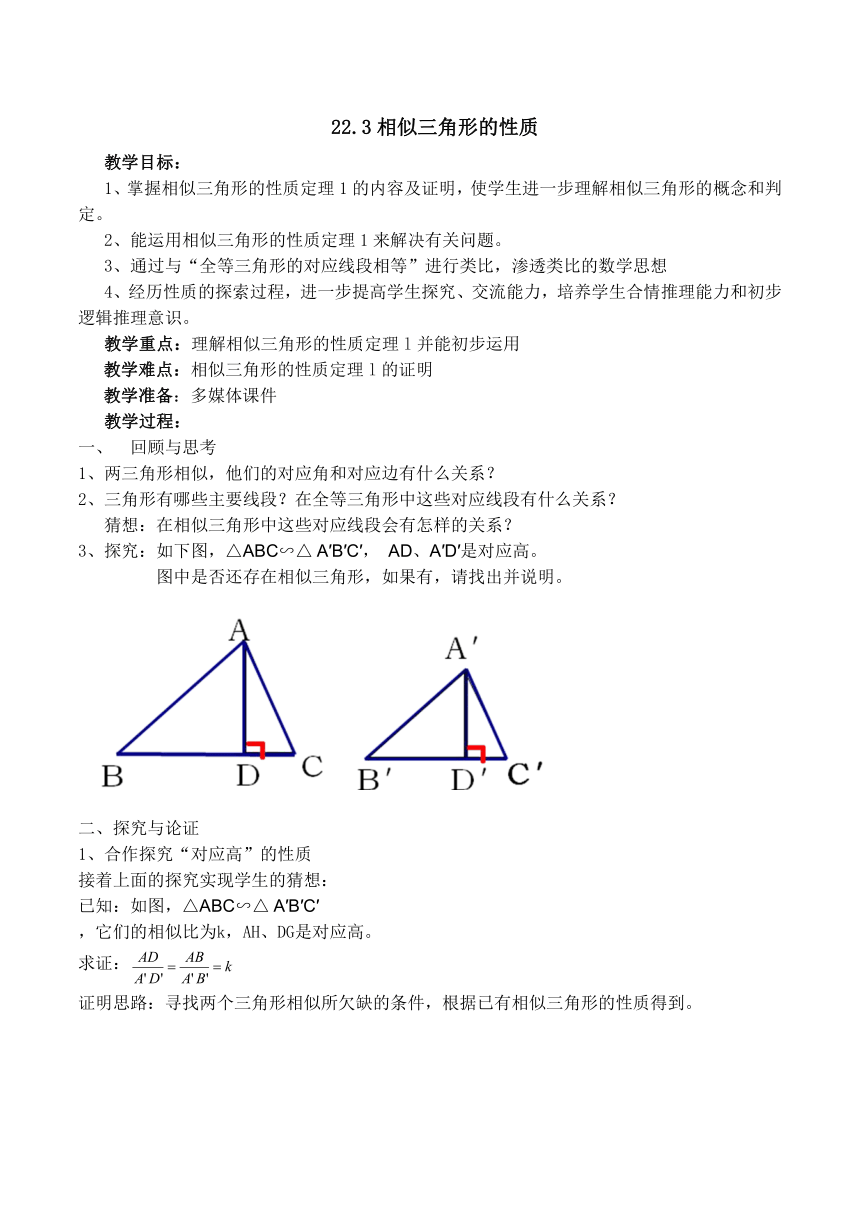
3、探究:如下图,△ABC∽△ A′B′C′, AD、A′D′是对应高。
图中是否还存在相似三角形,如果有,请找出并说明。
二、探究与论证
1、合作探究“对应高”的性质
接着上面的探究实现学生的猜想:
已知:如图,△ABC∽△ A′B′C′
,它们的相似比为k,AH、DG是对应高。
求证:
证明思路:寻找两个三角形相似所欠缺的条件,根据已有相似三角形的性质得到。
从而归纳:相似三角形对应高之比等于相似比。
2、自主探究“对应角平分线和中线”性质
类比“对应高”性质的证明过程,教师做好铺垫,组织学生合作探究。
鼓励学生自己画图,并写出“已知、求证”,教师点拨纠正。
从而归纳:相似三角形对应角平分线和中线之比等于相似比
3、综合归纳:
定理1:相似三角形对应高的比、对应中线的比、对应角平分线的比都等于相似比。
三、实践与应用
例1:已知:△ABC∽△DEF,BC=3.6cm,EF=6cm,AH是△ABC的一条高,且AH=2.4cm,
求:△DEF的高DG的长。
变式: AH、DG分别改为相应的角平分线和中线
例2:电灯位于直径为1.8米的圆桌的正上方3米处,圆桌与地面保持平行,并且在灯光下有直径为2.4米的圆形影子。请求灯泡距离地面的高度。
引导学生认真审题,画出示意图,明确已知条件,主动联想本节课所学新知识求解。
四、小结与提高
本节主要学习了性质定理1及其证明,重点要掌握综合运用相似三角形的判定与性质的思维方法,解题运用时要注意“对应”。
五、作业与拓展
1、教材P90-91:习题2、3、10
2、自学:教材P88 :例1
教学目标:
1、掌握相似三角形的性质定理1的内容及证明,使学生进一步理解相似三角形的概念和判定。
2、能运用相似三角形的性质定理1来解决有关问题。
3、通过与“全等三角形的对应线段相等”进行类比,渗透类比的数学思想
4、经历性质的探索过程,进一步提高学生探究、交流能力,培养学生合情推理能力和初步逻辑推理意识。
教学重点:理解相似三角形的性质定理l并能初步运用
教学难点:相似三角形的性质定理l的证明
教学准备:多媒体课件
教学过程:
回顾与思考
1、两三角形相似,他们的对应角和对应边有什么关系?
2、三角形有哪些主要线段?在全等三角形中这些对应线段有什么关系?
猜想:在相似三角形中这些对应线段会有怎样的关系?
3、探究:如下图,△ABC∽△ A′B′C′, AD、A′D′是对应高。
图中是否还存在相似三角形,如果有,请找出并说明。
二、探究与论证
1、合作探究“对应高”的性质
接着上面的探究实现学生的猜想:
已知:如图,△ABC∽△ A′B′C′
,它们的相似比为k,AH、DG是对应高。
求证:
证明思路:寻找两个三角形相似所欠缺的条件,根据已有相似三角形的性质得到。
从而归纳:相似三角形对应高之比等于相似比。
2、自主探究“对应角平分线和中线”性质
类比“对应高”性质的证明过程,教师做好铺垫,组织学生合作探究。
鼓励学生自己画图,并写出“已知、求证”,教师点拨纠正。
从而归纳:相似三角形对应角平分线和中线之比等于相似比
3、综合归纳:
定理1:相似三角形对应高的比、对应中线的比、对应角平分线的比都等于相似比。
三、实践与应用
例1:已知:△ABC∽△DEF,BC=3.6cm,EF=6cm,AH是△ABC的一条高,且AH=2.4cm,
求:△DEF的高DG的长。
变式: AH、DG分别改为相应的角平分线和中线
例2:电灯位于直径为1.8米的圆桌的正上方3米处,圆桌与地面保持平行,并且在灯光下有直径为2.4米的圆形影子。请求灯泡距离地面的高度。
引导学生认真审题,画出示意图,明确已知条件,主动联想本节课所学新知识求解。
四、小结与提高
本节主要学习了性质定理1及其证明,重点要掌握综合运用相似三角形的判定与性质的思维方法,解题运用时要注意“对应”。
五、作业与拓展
1、教材P90-91:习题2、3、10
2、自学:教材P88 :例1
