沪科版数学九年级上册 23.2 解直角三角形 课件(共29张PPT)
文档属性
| 名称 | 沪科版数学九年级上册 23.2 解直角三角形 课件(共29张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 424.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-12-27 18:45:55 | ||
图片预览






文档简介
(共29张PPT)
解直角三角形
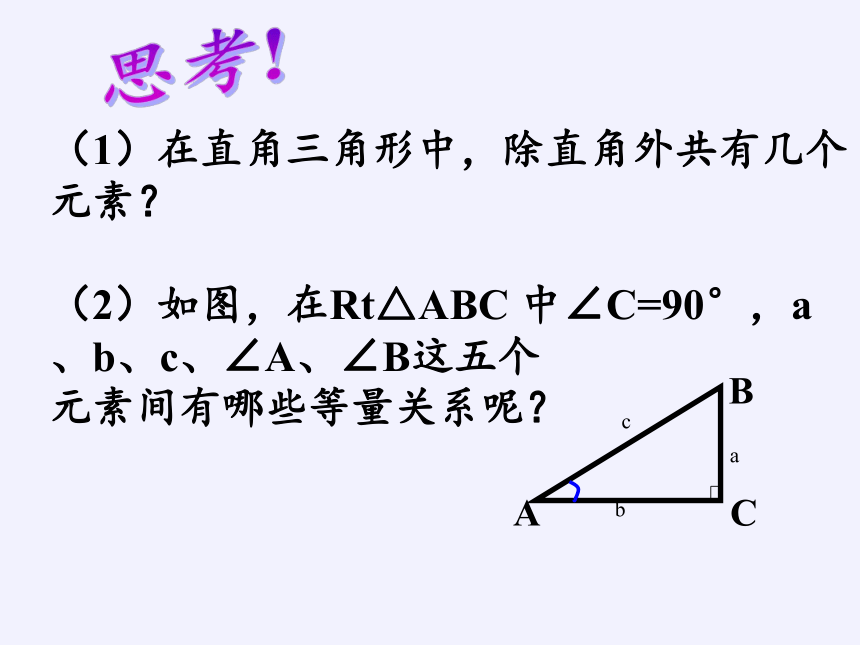
(1)在直角三角形中,除直角外共有几个 元素?
(2)如图,在Rt△ABC 中∠C=90°,a、b、c、∠A、∠B这五个
元素间有哪些等量关系呢?
A
B
C
c
b
a
思考!
定义:
由直角三角形中的已知元素,求出所有未知元素的过程,叫做解直角三角形.
问题:1.解直角三角形需要什么条件?
议议!
2.解直角三角形的条件可分为哪几类?
2.解直角三角形的条件可分为两大类:
①.已知一锐角、一边
(一锐角、一直角边或一斜边)
②.已知两边
(一直角边,一斜边或者两条直角边)
归纳:
1.解直角三角形除直角外,至少要知道两个元素(这两个元素中至少有一条边)
1.在Rt△ABC中,∠C=90°:
(1)已知a=4,c=8,解直角三角形.
(2)已知b=10,∠B=60°,解直角三角形.
(3)已知c=20,∠A=60°,解直角三角形.
(4)已知a=1,b= ,解直角三角形.
尝试!
“卡努” 台风将一棵大树刮断,经测量,大树刮断一端的着地点A到树根部C的距离为4米,倒下部分AB与地平面AC的夹角为400,你知道这棵大树有多高吗?
参考数据: (sin40°≈0.643; cos40° ≈0.766; tan40° ≈0.839)
40°
4米
解决问题
A
45°
则AB=____,
AC=_____, ∠A=_____
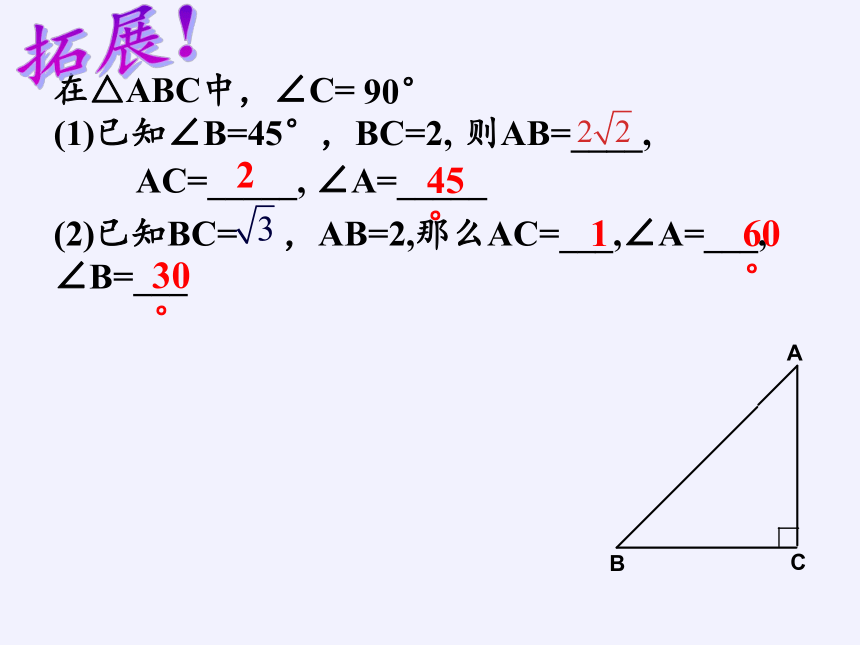
在△ABC中,∠C=
(1)已知∠B=45°,BC=2,
90°
(2)已知BC= ,AB=2,那么AC=___,∠A=___, ∠B=___
2
1
60°
30°
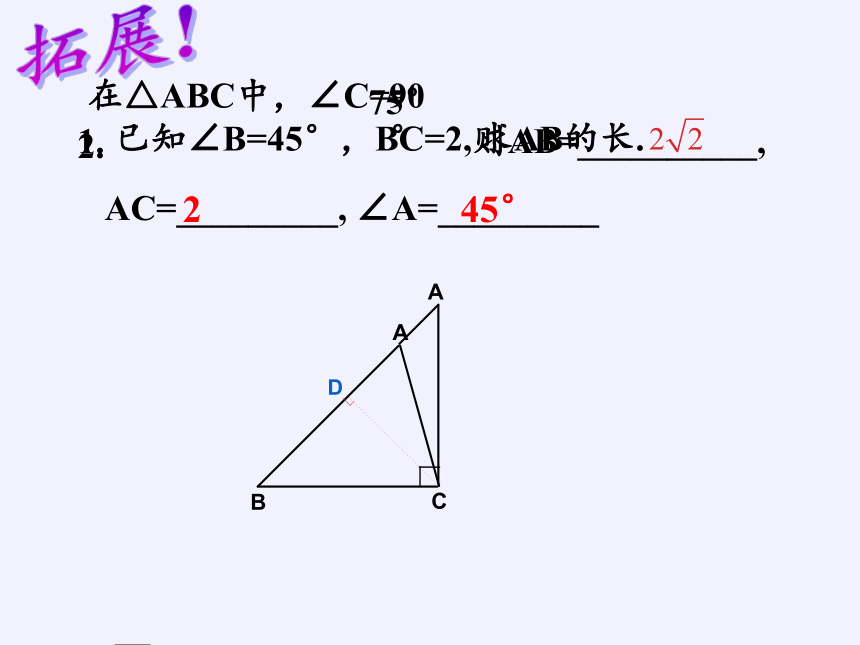
拓展!
1.
在△ABC中,∠C=
已知∠B=45°,BC=2,
2.
D
则AB=__________,
AC=_________, ∠A=_________
90°
2
45°
75°
求AB的长.
拓展!
拿出你事先准备的特殊直角三角形,拼一拼,你能给出其中的一些元素,求出某些元素的值吗?请试一试,然后派代表发言。
操作!
小组合作!
3.(2012安徽省10分)如图,在△ABC中,
∠A=30°,∠B=45°,AC= ,求AB的长
D
(2011安徽省10分)如图,某高速公路建设中需要确定隧道AB的长度.已知在离地面1500m高度C处的飞机上,测量人员测得正前方A、B两点处的俯角分别为60°和45°.求隧道AB的长(
≈1.73).
(2016年安徽第19题10分)如图,河的两岸l1与l2相互平行,A、B是l1上的两点,C、D是l2上的两点,某人在点A处测得∠CAB=90°,∠DAB=30°,再沿AB方向前进20米到达点E(点E在线段AB上),测得∠DEB=60°,求C、D两点间的距离.
(2013年安徽第19题10分).如图,防洪大堤的横截面是梯形ABCD,其中AD∥BC,坡角α=60°,汛期来临前对其进行了加固,改造后的背水面坡角β=45°。若原坡长AB=20m,求改造后的坡长AE.(结果保留根号)
(2010年安徽省第17题)如图,为了求河的宽度,在河对岸岸边任意取一点A,再在河这边沿河边取两点B、C,使得∠ABC=60°,∠ACB=45°,量得BC长为100米,求河的宽度(即求BC边上的高).
D
60°
45°
A
B
C
B
C
100米
D
(2015年安徽第18题8分)如图,平台AB高
为12m,在B处测得楼房CD顶部点D的仰角
为45°,底部点C的俯角为30°,求楼房CD的高度 。
B
D
C
60
A
E
30
50m
M
D
问题1楼房AB的高度是多少
问题2楼房CD的高度是多少
(2017年安徽第17题)如图,游客在点A处坐缆车出发,沿A-B-D的路线可至山顶D处,假设AB和BD都是线段,且AB=BD=600m,α=75°,β=45°求DE的长。(参考数据: )
45o
A
B
C
45o
B
C
A
45o
45o
C
A
B
60o
D
60o
D
翻转
B
C
A
45o
60o
D
旋转
E
45o
60o
A
B
D
C
旋转
平移
60o
D
30o
C
A
B
45o
D
平移
30o
C
A
B
45o
D
1、通过刚才的探究,我们可以得到解直角三角形的两种基本图形:
A
A
B
B
C
C
D
D
2、
现实对象
数学模型
实际问题的解
数学问题的解
数学抽象
逻辑推理
翻译回去
小结1
一题多解
如图,在四边形ABCD中, AB=2,CD=1, ∠A= 60°, ∠D= ∠B= 90°,求此四边形ABCD的面积。
A
B
C
D
2
60°
1
方法1
如图,在四边形ABCD中, AB=2,CD=1, ∠A= 60°, ∠D= ∠B= 90°,求此四边形ABCD的面积。
A
B
C
D
E
2
60°
1
A
B
C
D
E
2
1
60°
方法2
A
B
C
D
E
2
1
60°
F
方法3
A
B
C
D
2
1
60°
方法4
通过这节课的学习
在知识上你收获了......
在思想方法上......
今日事 今日毕
小结!
愿你拥有
一个能用数学思维思考世界的头脑。
一双能用数学视觉观察世界的眼睛;
必做题:P125第1,2题,全品两面。
选做题:一艘船向东航行,上午8时到达B处,看到有一灯塔在它的北偏东60°,距离为72海里的A处;上午10时到达C处,看到灯塔在它的正北方向.求这艘船航行的速度。(用根号表示)
布置作业!
谢 谢
解直角三角形
(1)在直角三角形中,除直角外共有几个 元素?
(2)如图,在Rt△ABC 中∠C=90°,a、b、c、∠A、∠B这五个
元素间有哪些等量关系呢?
A
B
C
c
b
a
思考!
定义:
由直角三角形中的已知元素,求出所有未知元素的过程,叫做解直角三角形.
问题:1.解直角三角形需要什么条件?
议议!
2.解直角三角形的条件可分为哪几类?
2.解直角三角形的条件可分为两大类:
①.已知一锐角、一边
(一锐角、一直角边或一斜边)
②.已知两边
(一直角边,一斜边或者两条直角边)
归纳:
1.解直角三角形除直角外,至少要知道两个元素(这两个元素中至少有一条边)
1.在Rt△ABC中,∠C=90°:
(1)已知a=4,c=8,解直角三角形.
(2)已知b=10,∠B=60°,解直角三角形.
(3)已知c=20,∠A=60°,解直角三角形.
(4)已知a=1,b= ,解直角三角形.
尝试!
“卡努” 台风将一棵大树刮断,经测量,大树刮断一端的着地点A到树根部C的距离为4米,倒下部分AB与地平面AC的夹角为400,你知道这棵大树有多高吗?
参考数据: (sin40°≈0.643; cos40° ≈0.766; tan40° ≈0.839)
40°
4米
解决问题
A
45°
则AB=____,
AC=_____, ∠A=_____
在△ABC中,∠C=
(1)已知∠B=45°,BC=2,
90°
(2)已知BC= ,AB=2,那么AC=___,∠A=___, ∠B=___
2
1
60°
30°
拓展!
1.
在△ABC中,∠C=
已知∠B=45°,BC=2,
2.
D
则AB=__________,
AC=_________, ∠A=_________
90°
2
45°
75°
求AB的长.
拓展!
拿出你事先准备的特殊直角三角形,拼一拼,你能给出其中的一些元素,求出某些元素的值吗?请试一试,然后派代表发言。
操作!
小组合作!
3.(2012安徽省10分)如图,在△ABC中,
∠A=30°,∠B=45°,AC= ,求AB的长
D
(2011安徽省10分)如图,某高速公路建设中需要确定隧道AB的长度.已知在离地面1500m高度C处的飞机上,测量人员测得正前方A、B两点处的俯角分别为60°和45°.求隧道AB的长(
≈1.73).
(2016年安徽第19题10分)如图,河的两岸l1与l2相互平行,A、B是l1上的两点,C、D是l2上的两点,某人在点A处测得∠CAB=90°,∠DAB=30°,再沿AB方向前进20米到达点E(点E在线段AB上),测得∠DEB=60°,求C、D两点间的距离.
(2013年安徽第19题10分).如图,防洪大堤的横截面是梯形ABCD,其中AD∥BC,坡角α=60°,汛期来临前对其进行了加固,改造后的背水面坡角β=45°。若原坡长AB=20m,求改造后的坡长AE.(结果保留根号)
(2010年安徽省第17题)如图,为了求河的宽度,在河对岸岸边任意取一点A,再在河这边沿河边取两点B、C,使得∠ABC=60°,∠ACB=45°,量得BC长为100米,求河的宽度(即求BC边上的高).
D
60°
45°
A
B
C
B
C
100米
D
(2015年安徽第18题8分)如图,平台AB高
为12m,在B处测得楼房CD顶部点D的仰角
为45°,底部点C的俯角为30°,求楼房CD的高度 。
B
D
C
60
A
E
30
50m
M
D
问题1楼房AB的高度是多少
问题2楼房CD的高度是多少
(2017年安徽第17题)如图,游客在点A处坐缆车出发,沿A-B-D的路线可至山顶D处,假设AB和BD都是线段,且AB=BD=600m,α=75°,β=45°求DE的长。(参考数据: )
45o
A
B
C
45o
B
C
A
45o
45o
C
A
B
60o
D
60o
D
翻转
B
C
A
45o
60o
D
旋转
E
45o
60o
A
B
D
C
旋转
平移
60o
D
30o
C
A
B
45o
D
平移
30o
C
A
B
45o
D
1、通过刚才的探究,我们可以得到解直角三角形的两种基本图形:
A
A
B
B
C
C
D
D
2、
现实对象
数学模型
实际问题的解
数学问题的解
数学抽象
逻辑推理
翻译回去
小结1
一题多解
如图,在四边形ABCD中, AB=2,CD=1, ∠A= 60°, ∠D= ∠B= 90°,求此四边形ABCD的面积。
A
B
C
D
2
60°
1
方法1
如图,在四边形ABCD中, AB=2,CD=1, ∠A= 60°, ∠D= ∠B= 90°,求此四边形ABCD的面积。
A
B
C
D
E
2
60°
1
A
B
C
D
E
2
1
60°
方法2
A
B
C
D
E
2
1
60°
F
方法3
A
B
C
D
2
1
60°
方法4
通过这节课的学习
在知识上你收获了......
在思想方法上......
今日事 今日毕
小结!
愿你拥有
一个能用数学思维思考世界的头脑。
一双能用数学视觉观察世界的眼睛;
必做题:P125第1,2题,全品两面。
选做题:一艘船向东航行,上午8时到达B处,看到有一灯塔在它的北偏东60°,距离为72海里的A处;上午10时到达C处,看到灯塔在它的正北方向.求这艘船航行的速度。(用根号表示)
布置作业!
谢 谢
