沪科版数学九年级上册 第22章 相似形 复习 课件(共18张PPT)
文档属性
| 名称 | 沪科版数学九年级上册 第22章 相似形 复习 课件(共18张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 510.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-12-27 23:01:40 | ||
图片预览






文档简介
(共18张PPT)
第22章 相似形 复习课件
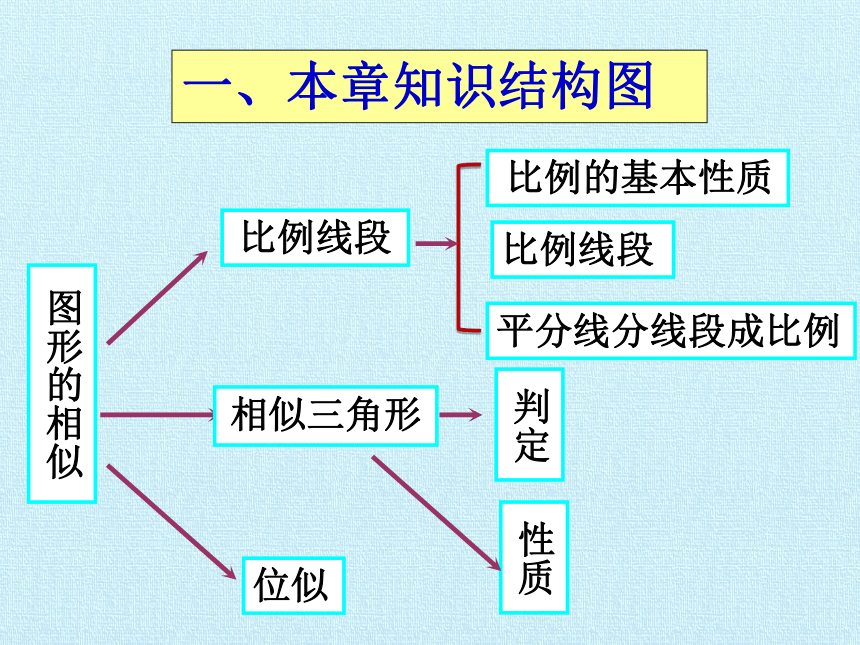
一、本章知识结构图
图形的相似
相似三角形
判定
性质
比例线段
位似
比例的基本性质
比例线段
平分线分线段成比例
一、成比例线段
对于四条线段a、b、c、d,如果其中两条线段的长度的比等于另外两条线段的比, 如 (或a∶b=c∶d),那么,这四条线段叫做成比例线段,简称比例线段。此时也称这四条线段成比例。
回顾与思考
如果 (b=d=f≠0),
那么
线段的比要注意以下几点:
线段的比是正数
单位要统一
线段的比与线段的长度无关
如果, 那么ad=bc。
如果ad=bc (a、b、c、d都不等于0),
那么
1、各角对应相等,各边对应成比例的两个多边形叫相似多边形。
2、三个角对应相等,三条边对应成比例的两个三角形叫相似三角形。两个相似三角形用“∽”表示,读做“相似于”。
3、相似三角形对应边的比,叫做相似比
二、相似图形
如△A1B1C1与△ABC相似,
注意:对应顶点写 在对应位置上
记作“△A1B1C1∽△ABC”
相似比=对应边的比值=
相似三角形的性质
对应角相等、对应边成比例
对应高之比、对应中线之比、对应角平分线之比都等于相似比
周长之比等于相似比
面积之比等于相似比的平方
相似三角形
方法2:平行于三角形一边的直线与其他两边(或延长线)相交,所构成的三角形与原三角形相似;
方法5:三边对应成比例的,两三角形相似。
相似三角形的判定方法
方法4:两边对应成比例且夹角相等,两三角形相似。
方法1:通过定义(不常用)
方法3:两对应角相等的,两三角形相似。
相似三角形的应用主要有两个方面:
(1) 测高
测量不能到达两点间的距离,常构造相似三角形求解。
(不能直接使用皮尺或刻度尺量的)
(不能直接测量的两点间的距离)
测量不能到达顶部的物体的高度,通常用“在同一时刻物高与影长成比例”的原理解决。
(2) 测距
三、相似三角形的应用
1.进行位似变换后得到的图形与原图形相似,对应点的连线都经过位似中心,对应顶点到位似中心的比等于相似比。
2.进行位似变换时,位似中心可以在图形的外部,也可以在图形的内部或图形的一边上,图形的顶点处。
3.画已知图形的位似图形时,要明确位似中心,相似比,以及两图形在位似中心的同侧或两侧。
四、位似图形的性质
三、典例精析,复习新知
复习训练,巩固提高
1.如图,AB∥CD,图中共有____对相似三角形。
2.如图,△ABC中,AB=AC,AD⊥BC于D,AE=EC,AD=18,BE=15,则△ABC的面积是______。
分析:作EF∥BC交AD于F。设BE交AD于O点,先求出OD长和OB长,最后用勾股定理求出BD的长。
6
144
第1题图
第2题图
C
D
谢 谢
第22章 相似形 复习课件
一、本章知识结构图
图形的相似
相似三角形
判定
性质
比例线段
位似
比例的基本性质
比例线段
平分线分线段成比例
一、成比例线段
对于四条线段a、b、c、d,如果其中两条线段的长度的比等于另外两条线段的比, 如 (或a∶b=c∶d),那么,这四条线段叫做成比例线段,简称比例线段。此时也称这四条线段成比例。
回顾与思考
如果 (b=d=f≠0),
那么
线段的比要注意以下几点:
线段的比是正数
单位要统一
线段的比与线段的长度无关
如果, 那么ad=bc。
如果ad=bc (a、b、c、d都不等于0),
那么
1、各角对应相等,各边对应成比例的两个多边形叫相似多边形。
2、三个角对应相等,三条边对应成比例的两个三角形叫相似三角形。两个相似三角形用“∽”表示,读做“相似于”。
3、相似三角形对应边的比,叫做相似比
二、相似图形
如△A1B1C1与△ABC相似,
注意:对应顶点写 在对应位置上
记作“△A1B1C1∽△ABC”
相似比=对应边的比值=
相似三角形的性质
对应角相等、对应边成比例
对应高之比、对应中线之比、对应角平分线之比都等于相似比
周长之比等于相似比
面积之比等于相似比的平方
相似三角形
方法2:平行于三角形一边的直线与其他两边(或延长线)相交,所构成的三角形与原三角形相似;
方法5:三边对应成比例的,两三角形相似。
相似三角形的判定方法
方法4:两边对应成比例且夹角相等,两三角形相似。
方法1:通过定义(不常用)
方法3:两对应角相等的,两三角形相似。
相似三角形的应用主要有两个方面:
(1) 测高
测量不能到达两点间的距离,常构造相似三角形求解。
(不能直接使用皮尺或刻度尺量的)
(不能直接测量的两点间的距离)
测量不能到达顶部的物体的高度,通常用“在同一时刻物高与影长成比例”的原理解决。
(2) 测距
三、相似三角形的应用
1.进行位似变换后得到的图形与原图形相似,对应点的连线都经过位似中心,对应顶点到位似中心的比等于相似比。
2.进行位似变换时,位似中心可以在图形的外部,也可以在图形的内部或图形的一边上,图形的顶点处。
3.画已知图形的位似图形时,要明确位似中心,相似比,以及两图形在位似中心的同侧或两侧。
四、位似图形的性质
三、典例精析,复习新知
复习训练,巩固提高
1.如图,AB∥CD,图中共有____对相似三角形。
2.如图,△ABC中,AB=AC,AD⊥BC于D,AE=EC,AD=18,BE=15,则△ABC的面积是______。
分析:作EF∥BC交AD于F。设BE交AD于O点,先求出OD长和OB长,最后用勾股定理求出BD的长。
6
144
第1题图
第2题图
C
D
谢 谢
