沪科版数学九年级上册 22.2 相似三角形的判定(课件)(共20张PPT)
文档属性
| 名称 | 沪科版数学九年级上册 22.2 相似三角形的判定(课件)(共20张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 2.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-12-28 07:13:07 | ||
图片预览



文档简介
(共20张PPT)
24.2
相似三角形的判定
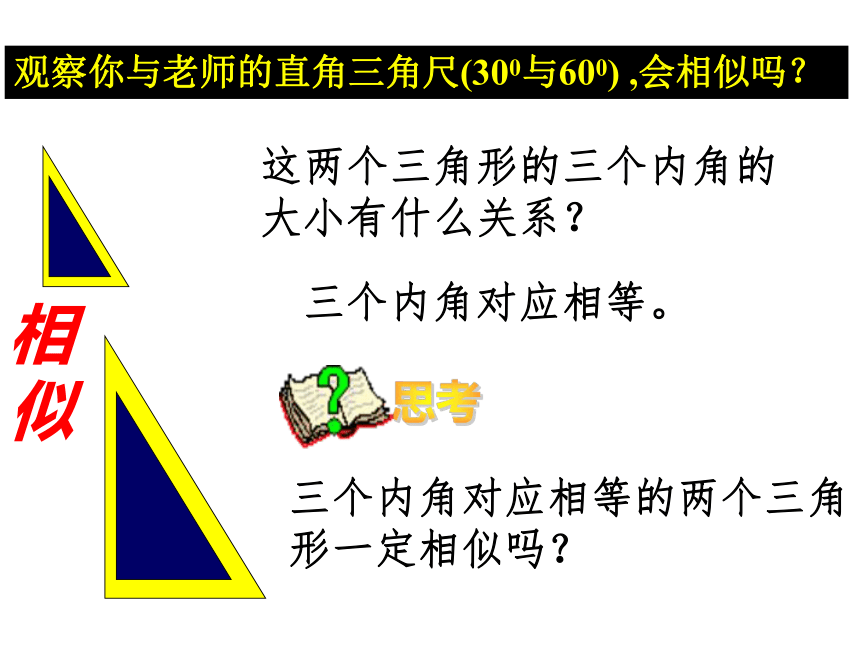
这两个三角形的三个内角的大小有什么关系?
三个内角对应相等的两个三角形一定相似吗?
三个内角对应相等。
观察你与老师的直角三角尺(300与600) ,会相似吗?
相
似
画一个三角形 ,使三个角分别为60°,45°,75° 。
①同桌分别量出两个三角形三边的长度;
②判断这两个三角形相似吗
即: 如果一个三角形的三个角与另一个三角形的三个角对应相等,那么这两个三角形_______.
相似
猜想: 如果一个三角形的两个角与另一个三角形的两个角对应相等,那么这两个三角形相似.
C
A
A'
B
B'
C'
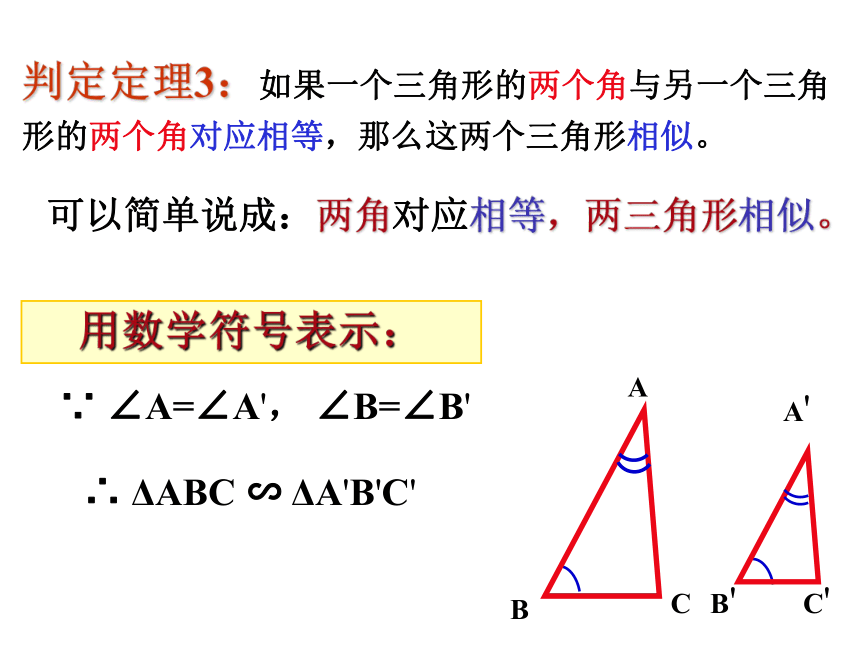
∵ ∠A=∠A', ∠B=∠B'
∴ ΔABC ∽ ΔA'B'C'
用数学符号表示:
判定定理3:如果一个三角形的两个角与另一个三角形的两个角对应相等,那么这两个三角形相似。
可以简单说成:两角对应相等,两三角形相似。
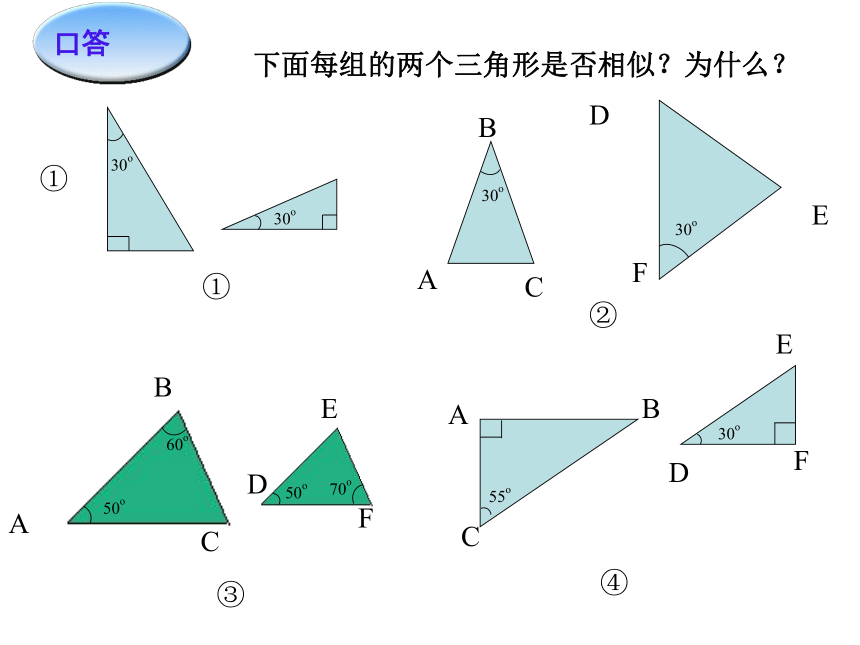
下面每组的两个三角形是否相似?为什么?
①
①
②
③
④
70o
50o
A
B
C
F
D
E
A
C
B
D
E
F
B
A
C
D
F
E
30o
30o
30o
30o
55o
30o
60o
50o
口答
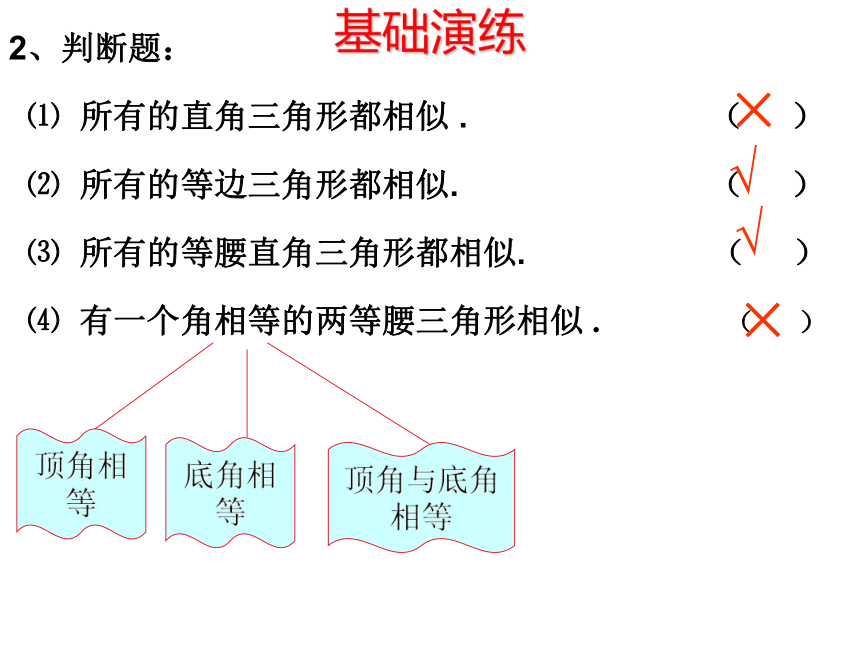
2、判断题:
⑴ 所有的直角三角形都相似 . ( )
⑵ 所有的等边三角形都相似. ( )
⑶ 所有的等腰直角三角形都相似. ( )
⑷ 有一个角相等的两等腰三角形相似 . ( )
×
√
√
×
顶角相等
底角相等
顶角与底角相等
基础演练
3、如果,当∠ACD满足什么条件时,
△ACD∽△ABC?
A
C
B
D
答案: ∠ACD= ∠ABC
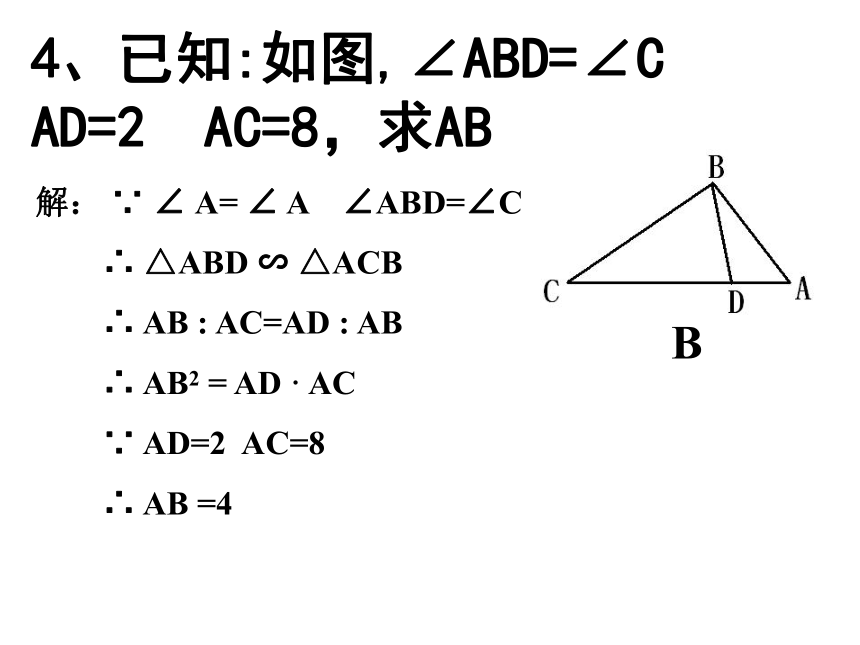
解: ∵ ∠ A= ∠ A ∠ABD=∠C
∴ △ABD ∽ △ACB
∴ AB : AC=AD : AB
∴ AB2 = AD · AC
∵ AD=2 AC=8
∴ AB =4
4、已知:如图,∠ABD=∠C AD=2 AC=8,求AB
B
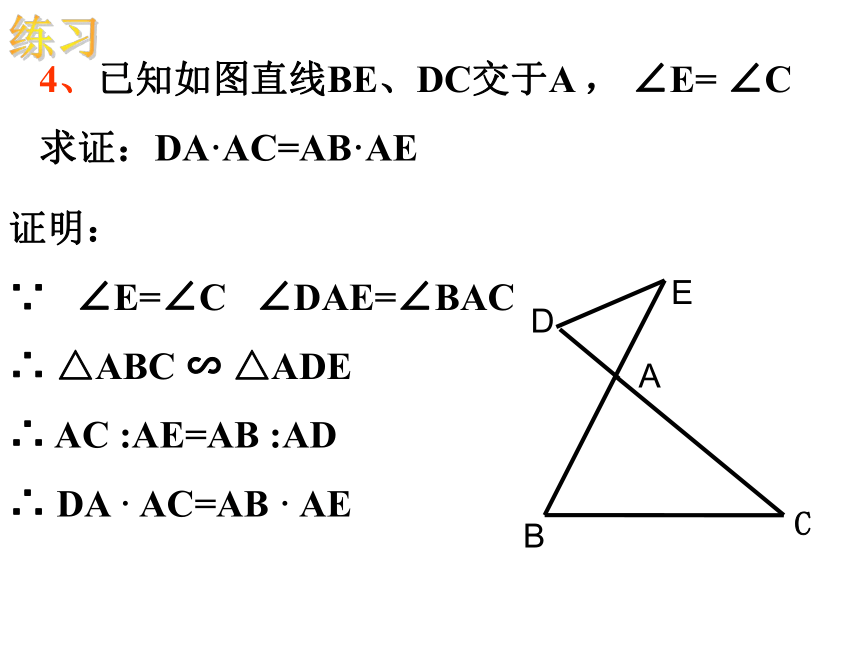
4、已知如图直线BE、DC交于A , ∠E= ∠C
求证:DA·AC=AB·AE
D
E
A
B
C
证明:
∵ ∠E=∠C ∠DAE=∠BAC
∴ △ABC ∽ △ADE
∴ AC :AE=AB :AD
∴ DA · AC=AB · AE
解: ∵ ∠ A= ∠ A ∠ABD=∠C
∴ △ABD ∽ △ACB
∴ AB : AC=AD : AB
∴ AB2 = AD · AC
∵ AD=2 AC=8
∴ AB =4
5.已知如图, ∠ABD=∠C
AD=2 ,AC=8,求AB
A
B
C
D
A
B
C
D
E
A
B
C
D
E
2
1
O
C
B
A
D
O
C
D
A
B
A
B
C
D
E
不经历风雨,怎么见彩虹
没有人能随随便便成功!
A
B
C
A’
B’
C’
基础演练
1、下列图形中两个三角形是否相似?
A
B
C
D
E
A
B
C
A’
C’
B’
A
B
C
D
E
(1)
(2)
(3)
(4)
思 考
(1)如果两个等腰三角形有一对底角对应相等那么它
们是否一定相似 有一对顶角对应相等呢
(2)有一个角等于300的两个等腰三角形是否相似
等于1200呢
如图,AD⊥BC于点D, CE⊥AB于点 E ,且交AD于F,你能从中找出几对相似三角形?
B
C
A
E
D
F
A
B
C
D
E
已知D、E分别是△ABC的边AB,AC上的点,若∠A=35°, ∠C=85°,∠AED=60 °
求证:AD·AB= AE·AC
△ACD ∽ △ CBD∽ △ ABC
例2:找出图中所有的相似三角形。
“双垂直”三角形
B
D
A
C
有三对相似三角形:
△ACD∽ △CBD
△CBD∽ △ABC
△ACD∽ △ABC
常用的成比例的线段:
常用的相等的角:
∠A =∠DCB ;∠B =∠ACD
B
D
A
C
2、已知:如图,BD、CE是△ABC的高,
请找出图中所有的相似三角形并说明理由。
A
B
C
D
E
5、如图:在Rt △ ABC中, ∠ABC=900,BD⊥AC于D
A
B
D
C
E
F
问:若E是BC中点,ED的延长线交BA的延长线于F,
求证:AB : AC=DF : BF
24.2
相似三角形的判定
这两个三角形的三个内角的大小有什么关系?
三个内角对应相等的两个三角形一定相似吗?
三个内角对应相等。
观察你与老师的直角三角尺(300与600) ,会相似吗?
相
似
画一个三角形 ,使三个角分别为60°,45°,75° 。
①同桌分别量出两个三角形三边的长度;
②判断这两个三角形相似吗
即: 如果一个三角形的三个角与另一个三角形的三个角对应相等,那么这两个三角形_______.
相似
猜想: 如果一个三角形的两个角与另一个三角形的两个角对应相等,那么这两个三角形相似.
C
A
A'
B
B'
C'
∵ ∠A=∠A', ∠B=∠B'
∴ ΔABC ∽ ΔA'B'C'
用数学符号表示:
判定定理3:如果一个三角形的两个角与另一个三角形的两个角对应相等,那么这两个三角形相似。
可以简单说成:两角对应相等,两三角形相似。
下面每组的两个三角形是否相似?为什么?
①
①
②
③
④
70o
50o
A
B
C
F
D
E
A
C
B
D
E
F
B
A
C
D
F
E
30o
30o
30o
30o
55o
30o
60o
50o
口答
2、判断题:
⑴ 所有的直角三角形都相似 . ( )
⑵ 所有的等边三角形都相似. ( )
⑶ 所有的等腰直角三角形都相似. ( )
⑷ 有一个角相等的两等腰三角形相似 . ( )
×
√
√
×
顶角相等
底角相等
顶角与底角相等
基础演练
3、如果,当∠ACD满足什么条件时,
△ACD∽△ABC?
A
C
B
D
答案: ∠ACD= ∠ABC
解: ∵ ∠ A= ∠ A ∠ABD=∠C
∴ △ABD ∽ △ACB
∴ AB : AC=AD : AB
∴ AB2 = AD · AC
∵ AD=2 AC=8
∴ AB =4
4、已知:如图,∠ABD=∠C AD=2 AC=8,求AB
B
4、已知如图直线BE、DC交于A , ∠E= ∠C
求证:DA·AC=AB·AE
D
E
A
B
C
证明:
∵ ∠E=∠C ∠DAE=∠BAC
∴ △ABC ∽ △ADE
∴ AC :AE=AB :AD
∴ DA · AC=AB · AE
解: ∵ ∠ A= ∠ A ∠ABD=∠C
∴ △ABD ∽ △ACB
∴ AB : AC=AD : AB
∴ AB2 = AD · AC
∵ AD=2 AC=8
∴ AB =4
5.已知如图, ∠ABD=∠C
AD=2 ,AC=8,求AB
A
B
C
D
A
B
C
D
E
A
B
C
D
E
2
1
O
C
B
A
D
O
C
D
A
B
A
B
C
D
E
不经历风雨,怎么见彩虹
没有人能随随便便成功!
A
B
C
A’
B’
C’
基础演练
1、下列图形中两个三角形是否相似?
A
B
C
D
E
A
B
C
A’
C’
B’
A
B
C
D
E
(1)
(2)
(3)
(4)
思 考
(1)如果两个等腰三角形有一对底角对应相等那么它
们是否一定相似 有一对顶角对应相等呢
(2)有一个角等于300的两个等腰三角形是否相似
等于1200呢
如图,AD⊥BC于点D, CE⊥AB于点 E ,且交AD于F,你能从中找出几对相似三角形?
B
C
A
E
D
F
A
B
C
D
E
已知D、E分别是△ABC的边AB,AC上的点,若∠A=35°, ∠C=85°,∠AED=60 °
求证:AD·AB= AE·AC
△ACD ∽ △ CBD∽ △ ABC
例2:找出图中所有的相似三角形。
“双垂直”三角形
B
D
A
C
有三对相似三角形:
△ACD∽ △CBD
△CBD∽ △ABC
△ACD∽ △ABC
常用的成比例的线段:
常用的相等的角:
∠A =∠DCB ;∠B =∠ACD
B
D
A
C
2、已知:如图,BD、CE是△ABC的高,
请找出图中所有的相似三角形并说明理由。
A
B
C
D
E
5、如图:在Rt △ ABC中, ∠ABC=900,BD⊥AC于D
A
B
D
C
E
F
问:若E是BC中点,ED的延长线交BA的延长线于F,
求证:AB : AC=DF : BF
