1.3动量守恒定律(第二课时)课件(17张PPT)
文档属性
| 名称 | 1.3动量守恒定律(第二课时)课件(17张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 2.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(2019) | ||
| 科目 | 物理 | ||
| 更新时间 | 2021-12-26 20:34:05 | ||
图片预览





文档简介
第一章 动量守恒定律
1.3:动量守恒定律
(第二课时)
如果一个系统不受外力,或者所受外力的矢量和为0,
这个系统的总动量保持不变。这就是动量守恒定律。
1.内容:
2.表达式:
(3)Δp=0
(系统总动量的变化量为零)
(1)p=p′或m1v1+m2v2=m1v1′+m2v2′
(系统作用前的总动量等于作用后的总动量).
(2)Δp1=-Δp2 或 m1Δv1=-m2Δv2
(系统内一个物体的动量变化与另一物体的动量变化等大反向)
知识回顾
(1) 理想条件:系统内的任何物体都不受外力作用。
(2) 实际条件:系统虽然受到外力,但是系统所受外力的矢量和为零。
3.适用条件:
知识回顾
(3) 近似条件:系统所受合力不为零,但系统内力远大于外力。
(4) 单向条件:系统在某一方向上合力为0,则该方向动量守恒。
矢量性:动量守恒表达式是一个矢量表达式,对于作用前后的运动方向都在同一直线上的问题,应选取统一的正方向。
瞬时性:动量是一个状态量,动量守恒指的是任意时刻的动量相同。
相对性:定律中的速度都是相对于同一参考系的,一般以地球为参考系。
普适性:不仅适用于低速宏观的系统,也适用于高速(接近光速)、微观(小到分子、原子的尺度)的系统。
4.理解
知识回顾
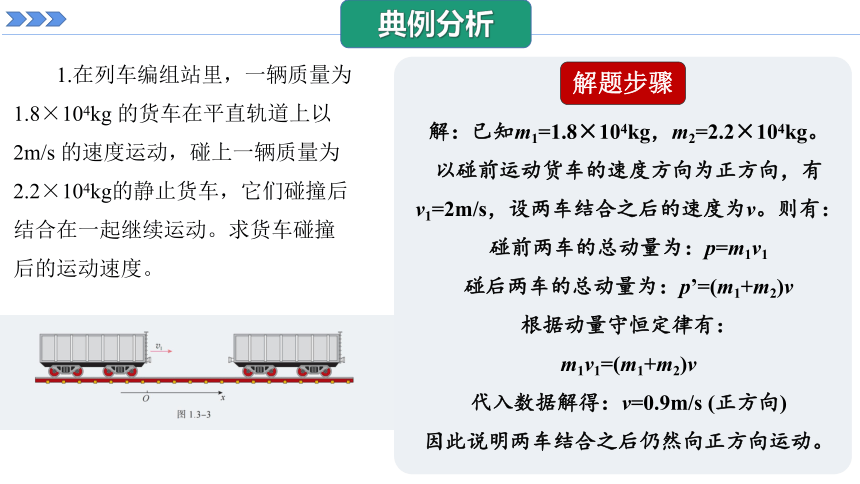
1.在列车编组站里,一辆质量为1.8×104kg 的货车在平直轨道上以2m/s 的速度运动,碰上一辆质量为2.2×104kg的静止货车,它们碰撞后结合在一起继续运动。求货车碰撞后的运动速度。
典例分析
思维引导
① 研究对象:运动的货车与静止的货车组成的系统。(该系统的动量是否守恒?为什么?)
② 研究过程:可以将碰前定为初状态,碰后一起运动定为末状态。
③ 定正方向:选取运动货车的初速度方向为正,分别表示碰前和碰后系统的速度。(对地速度)
④ 列式求解:根据系统的动量守恒列出方程,等号左边为初动量,右边为末动量。
1.在列车编组站里,一辆质量为1.8×104kg 的货车在平直轨道上以2m/s 的速度运动,碰上一辆质量为2.2×104kg的静止货车,它们碰撞后结合在一起继续运动。求货车碰撞后的运动速度。
典例分析
解题步骤
解:已知m1=1.8×104kg,m2=2.2×104kg。以碰前运动货车的速度方向为正方向,有v1=2m/s,设两车结合之后的速度为v。则有:
碰前两车的总动量为:p=m1v1
碰后两车的总动量为:p’=(m1+m2)v
根据动量守恒定律有:
m1v1=(m1+m2)v
代入数据解得:v=0.9m/s (正方向)
因此说明两车结合之后仍然向正方向运动。
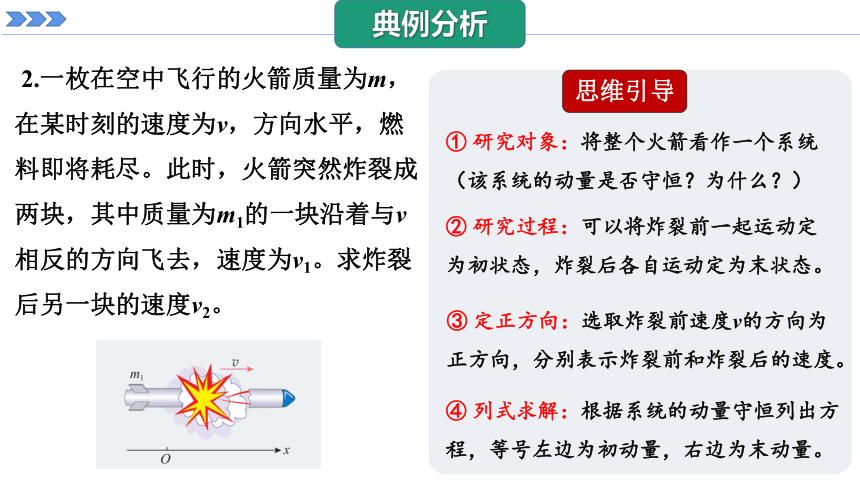
2.一枚在空中飞行的火箭质量为m,在某时刻的速度为v,方向水平,燃料即将耗尽。此时,火箭突然炸裂成两块,其中质量为m1的一块沿着与v相反的方向飞去,速度为v1。求炸裂后另一块的速度v2。
典例分析
思维引导
① 研究对象:将整个火箭看作一个系统(该系统的动量是否守恒?为什么?)
② 研究过程:可以将炸裂前一起运动定为初状态,炸裂后各自运动定为末状态。
③ 定正方向:选取炸裂前速度v的方向为正方向,分别表示炸裂前和炸裂后的速度。
④ 列式求解:根据系统的动量守恒列出方程,等号左边为初动量,右边为末动量。
典例分析
解题步骤
解:以炸裂前火箭速度方向为正方向,则有:
炸裂前火箭的总动量为:p=mv
炸裂后火箭的总动量为:p’=-m1v1+(m-m1)v2
根据动量守恒定律有:
mv=-m1v1+(m-m1)v2
代入数据解得:????2=????????+????1????1?????????1 (正方向)
因此说明炸裂后另一块仍然向正方向运动。
?
2.一枚在空中飞行的火箭质量为m,在某时刻的速度为v,方向水平,燃料即将耗尽。此时,火箭突然炸裂成两块,其中质量为m1的一块沿着与v相反的方向飞去,速度为v1。求炸裂后另一块的速度v2。
⑴找:找研究对象(系统包括那几个物体)和研究过程;
⑵析:进行受力分析,判断系统动量是否守恒(或在某一方向是否守恒);
⑶定:规定正方向,确定初末状态动量正负号;
⑷列:由动量守恒定律列方程;
⑸解:解方程,得出最后的结果,并对结果进行分析。
应用动量守恒定律解题的基本步骤和方法
m1v1+m2v2=m1v1′+m2v2′
典例分析
2.一枚在空中飞行的火箭质量为m,在某时刻的速度为v,方向水平,燃料即将耗尽。此时,火箭突然炸裂成两块,其中质量为m1的一块沿着与v相反的方向飞去,速度为v1。求炸裂后另一块的速度v2。
思考:火箭在炸裂前后,系统的机械能守恒吗?如果机械能不守恒,机械能是怎样变化的?
机械能不守恒,炸药化学能转化为机械能,所以系统机械能增加。
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}
机械能守恒定律
动量守恒定律
研究对象
相互作用的物体组成的系统
相互作用的物体组成的系统
守恒条件
只有重力或弹力做功的物体系统内,其他力不做功
系统不受外力或所受外力的合力等于零
守恒性质
标量守恒(不考虑方向性)
矢量守恒(规定正方向)
适用范围
仅限于宏观、低速领域
到目前为止物理学研究的一切领域
联系
动量守恒定律和机械能守恒定律虽然可以运用理论推导出来,但重要的是它们都可以用实验来验证,因此它们都是实验规律。
注
意
这两个守恒定律的守恒条件不同而导致的必然结果。如各种爆炸、碰撞、反冲现象中,因
F内>>F外,动量是守恒的,但很多情况下有内力做功,有其他形式的能量转化为机械能,而使机械能不守恒.
1.质量为10g的子弹,以300m/s的速度射入质量是24g静止在光滑水平桌面上的木块。
(1)如果子弹留在木块中,木块运动的速度是多大?
(2)如果子弹把木块打穿,子弹穿过木块后的速度为100m/s ,这时木块的速度又是多大?
随堂练习
随堂练习
(2)根据动量守恒定律则有: m1v1 = m1v′1+ m2v′2
代入数据解得:v′2=2503 m/s
?
答:(1)子弹、木块构成的系统中,子弹受到重力作用,但子弹的重力,远小于二者相互作用的内力,因此该系统可以近似看作动量守恒。根据动量守恒定律有:m1v1 =(m1+m2)v,代入数据解得:v=150017 m/s
?
2.细线下吊着一个质量为 m1 的静止沙袋,沙袋到细线上端悬挂点的距离为 l。一颗质量为m 的子弹水平射入沙袋并留在沙袋中,随沙袋一起摆动。已知沙袋摆动时摆线的最大偏角是θ,求子弹射入沙袋前的速度。
随堂练习
2.细线下吊着一个质量为 m1 的静止沙袋,沙袋到细线上端悬挂点的距离为 l。一颗质量为m 的子弹水平射入沙袋并留在沙袋中,随沙袋一起摆动。已知沙袋摆动时摆线的最大偏角是θ,求子弹射入沙袋前的速度。
解:① 子弹打沙袋的过程中,子弹和沙袋动量守恒:mv0=(m+m1)v
② 从子弹留在沙袋中到随沙袋一起摆动θ角度
的过程中,系统机械能守恒:
(m+m1)v2/2=(m+m1)gl(1-cosθ)
③ 联立上述方程解得:
动量能量综合题
随堂练习
2.细线下吊着一个质量为 m1 的静止沙袋,沙袋到细线上端悬挂点的距离为 l。一颗质量为m 的子弹水平射入沙袋并留在沙袋中,随沙袋一起摆动。已知沙袋摆动时摆线的最大偏角是θ,求子弹射入沙袋前的速度。
解:子弹与沙袋相互作用的整个过程中,子弹和沙袋机械能守恒:
mv02/2=(m+m1)gl(1-cosθ)
这种解法对吗?若是错了,错在哪里?
动量能量综合题
子弹射入沙袋的过程中有机械能损失!
随堂练习
思维导图
1.3:动量守恒定律
(第二课时)
如果一个系统不受外力,或者所受外力的矢量和为0,
这个系统的总动量保持不变。这就是动量守恒定律。
1.内容:
2.表达式:
(3)Δp=0
(系统总动量的变化量为零)
(1)p=p′或m1v1+m2v2=m1v1′+m2v2′
(系统作用前的总动量等于作用后的总动量).
(2)Δp1=-Δp2 或 m1Δv1=-m2Δv2
(系统内一个物体的动量变化与另一物体的动量变化等大反向)
知识回顾
(1) 理想条件:系统内的任何物体都不受外力作用。
(2) 实际条件:系统虽然受到外力,但是系统所受外力的矢量和为零。
3.适用条件:
知识回顾
(3) 近似条件:系统所受合力不为零,但系统内力远大于外力。
(4) 单向条件:系统在某一方向上合力为0,则该方向动量守恒。
矢量性:动量守恒表达式是一个矢量表达式,对于作用前后的运动方向都在同一直线上的问题,应选取统一的正方向。
瞬时性:动量是一个状态量,动量守恒指的是任意时刻的动量相同。
相对性:定律中的速度都是相对于同一参考系的,一般以地球为参考系。
普适性:不仅适用于低速宏观的系统,也适用于高速(接近光速)、微观(小到分子、原子的尺度)的系统。
4.理解
知识回顾
1.在列车编组站里,一辆质量为1.8×104kg 的货车在平直轨道上以2m/s 的速度运动,碰上一辆质量为2.2×104kg的静止货车,它们碰撞后结合在一起继续运动。求货车碰撞后的运动速度。
典例分析
思维引导
① 研究对象:运动的货车与静止的货车组成的系统。(该系统的动量是否守恒?为什么?)
② 研究过程:可以将碰前定为初状态,碰后一起运动定为末状态。
③ 定正方向:选取运动货车的初速度方向为正,分别表示碰前和碰后系统的速度。(对地速度)
④ 列式求解:根据系统的动量守恒列出方程,等号左边为初动量,右边为末动量。
1.在列车编组站里,一辆质量为1.8×104kg 的货车在平直轨道上以2m/s 的速度运动,碰上一辆质量为2.2×104kg的静止货车,它们碰撞后结合在一起继续运动。求货车碰撞后的运动速度。
典例分析
解题步骤
解:已知m1=1.8×104kg,m2=2.2×104kg。以碰前运动货车的速度方向为正方向,有v1=2m/s,设两车结合之后的速度为v。则有:
碰前两车的总动量为:p=m1v1
碰后两车的总动量为:p’=(m1+m2)v
根据动量守恒定律有:
m1v1=(m1+m2)v
代入数据解得:v=0.9m/s (正方向)
因此说明两车结合之后仍然向正方向运动。
2.一枚在空中飞行的火箭质量为m,在某时刻的速度为v,方向水平,燃料即将耗尽。此时,火箭突然炸裂成两块,其中质量为m1的一块沿着与v相反的方向飞去,速度为v1。求炸裂后另一块的速度v2。
典例分析
思维引导
① 研究对象:将整个火箭看作一个系统(该系统的动量是否守恒?为什么?)
② 研究过程:可以将炸裂前一起运动定为初状态,炸裂后各自运动定为末状态。
③ 定正方向:选取炸裂前速度v的方向为正方向,分别表示炸裂前和炸裂后的速度。
④ 列式求解:根据系统的动量守恒列出方程,等号左边为初动量,右边为末动量。
典例分析
解题步骤
解:以炸裂前火箭速度方向为正方向,则有:
炸裂前火箭的总动量为:p=mv
炸裂后火箭的总动量为:p’=-m1v1+(m-m1)v2
根据动量守恒定律有:
mv=-m1v1+(m-m1)v2
代入数据解得:????2=????????+????1????1?????????1 (正方向)
因此说明炸裂后另一块仍然向正方向运动。
?
2.一枚在空中飞行的火箭质量为m,在某时刻的速度为v,方向水平,燃料即将耗尽。此时,火箭突然炸裂成两块,其中质量为m1的一块沿着与v相反的方向飞去,速度为v1。求炸裂后另一块的速度v2。
⑴找:找研究对象(系统包括那几个物体)和研究过程;
⑵析:进行受力分析,判断系统动量是否守恒(或在某一方向是否守恒);
⑶定:规定正方向,确定初末状态动量正负号;
⑷列:由动量守恒定律列方程;
⑸解:解方程,得出最后的结果,并对结果进行分析。
应用动量守恒定律解题的基本步骤和方法
m1v1+m2v2=m1v1′+m2v2′
典例分析
2.一枚在空中飞行的火箭质量为m,在某时刻的速度为v,方向水平,燃料即将耗尽。此时,火箭突然炸裂成两块,其中质量为m1的一块沿着与v相反的方向飞去,速度为v1。求炸裂后另一块的速度v2。
思考:火箭在炸裂前后,系统的机械能守恒吗?如果机械能不守恒,机械能是怎样变化的?
机械能不守恒,炸药化学能转化为机械能,所以系统机械能增加。
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}
机械能守恒定律
动量守恒定律
研究对象
相互作用的物体组成的系统
相互作用的物体组成的系统
守恒条件
只有重力或弹力做功的物体系统内,其他力不做功
系统不受外力或所受外力的合力等于零
守恒性质
标量守恒(不考虑方向性)
矢量守恒(规定正方向)
适用范围
仅限于宏观、低速领域
到目前为止物理学研究的一切领域
联系
动量守恒定律和机械能守恒定律虽然可以运用理论推导出来,但重要的是它们都可以用实验来验证,因此它们都是实验规律。
注
意
这两个守恒定律的守恒条件不同而导致的必然结果。如各种爆炸、碰撞、反冲现象中,因
F内>>F外,动量是守恒的,但很多情况下有内力做功,有其他形式的能量转化为机械能,而使机械能不守恒.
1.质量为10g的子弹,以300m/s的速度射入质量是24g静止在光滑水平桌面上的木块。
(1)如果子弹留在木块中,木块运动的速度是多大?
(2)如果子弹把木块打穿,子弹穿过木块后的速度为100m/s ,这时木块的速度又是多大?
随堂练习
随堂练习
(2)根据动量守恒定律则有: m1v1 = m1v′1+ m2v′2
代入数据解得:v′2=2503 m/s
?
答:(1)子弹、木块构成的系统中,子弹受到重力作用,但子弹的重力,远小于二者相互作用的内力,因此该系统可以近似看作动量守恒。根据动量守恒定律有:m1v1 =(m1+m2)v,代入数据解得:v=150017 m/s
?
2.细线下吊着一个质量为 m1 的静止沙袋,沙袋到细线上端悬挂点的距离为 l。一颗质量为m 的子弹水平射入沙袋并留在沙袋中,随沙袋一起摆动。已知沙袋摆动时摆线的最大偏角是θ,求子弹射入沙袋前的速度。
随堂练习
2.细线下吊着一个质量为 m1 的静止沙袋,沙袋到细线上端悬挂点的距离为 l。一颗质量为m 的子弹水平射入沙袋并留在沙袋中,随沙袋一起摆动。已知沙袋摆动时摆线的最大偏角是θ,求子弹射入沙袋前的速度。
解:① 子弹打沙袋的过程中,子弹和沙袋动量守恒:mv0=(m+m1)v
② 从子弹留在沙袋中到随沙袋一起摆动θ角度
的过程中,系统机械能守恒:
(m+m1)v2/2=(m+m1)gl(1-cosθ)
③ 联立上述方程解得:
动量能量综合题
随堂练习
2.细线下吊着一个质量为 m1 的静止沙袋,沙袋到细线上端悬挂点的距离为 l。一颗质量为m 的子弹水平射入沙袋并留在沙袋中,随沙袋一起摆动。已知沙袋摆动时摆线的最大偏角是θ,求子弹射入沙袋前的速度。
解:子弹与沙袋相互作用的整个过程中,子弹和沙袋机械能守恒:
mv02/2=(m+m1)gl(1-cosθ)
这种解法对吗?若是错了,错在哪里?
动量能量综合题
子弹射入沙袋的过程中有机械能损失!
随堂练习
思维导图
