2021--2022学年人教版七年级数学下册5.1.1 相交线 同步训练(Word版含简答)
文档属性
| 名称 | 2021--2022学年人教版七年级数学下册5.1.1 相交线 同步训练(Word版含简答) | 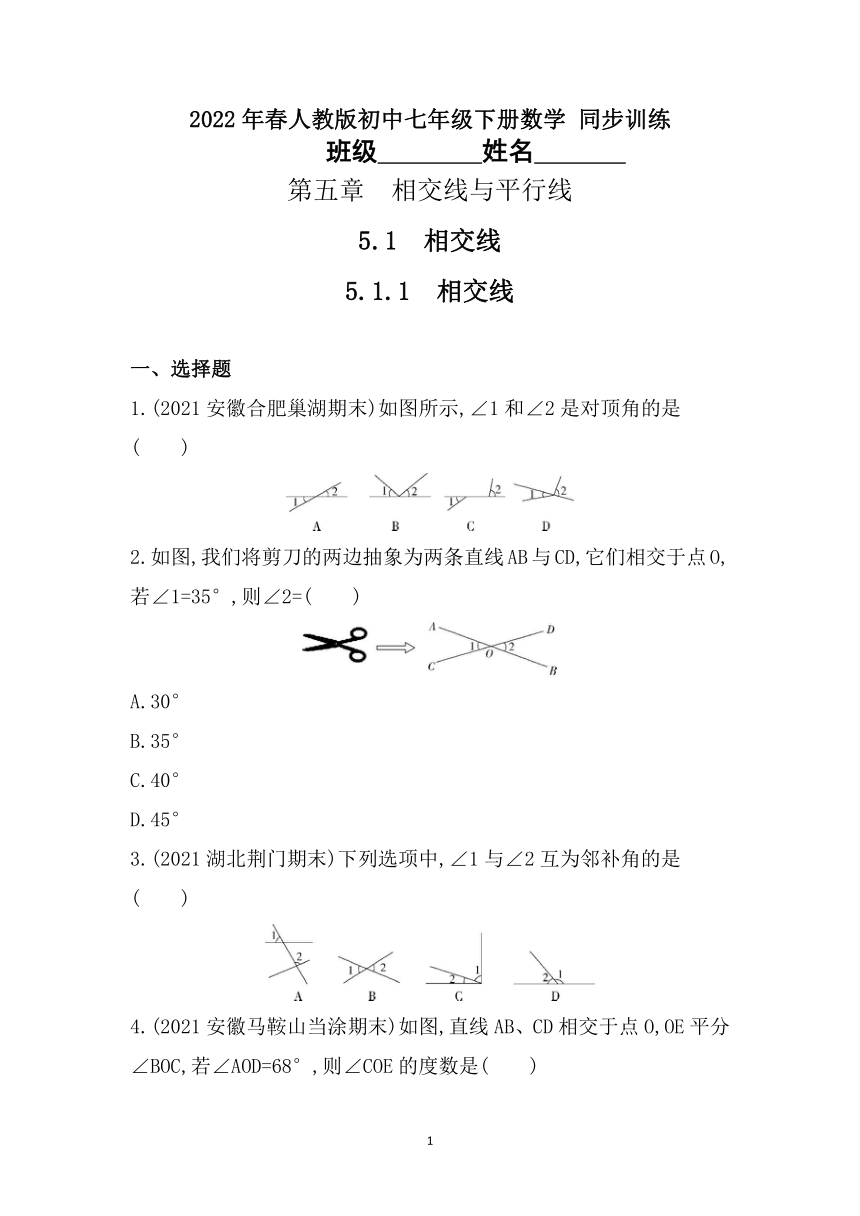 | |
| 格式 | doc | ||
| 文件大小 | 171.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-12-27 20:50:00 | ||
图片预览




文档简介
2022年春人教版初中七年级下册数学 同步训练
班级 姓名
第五章 相交线与平行线
5.1 相交线
5.1.1 相交线
一、选择题
1.(2021安徽合肥巢湖期末)如图所示,∠1和∠2是对顶角的是( )
2.如图,我们将剪刀的两边抽象为两条直线AB与CD,它们相交于点O,若∠1=35°,则∠2=( )
A.30°
B.35°
C.40°
D.45°
3.(2021湖北荆门期末)下列选项中,∠1与∠2互为邻补角的是( )
4.(2021安徽马鞍山当涂期末)如图,直线AB、CD相交于点O,OE平分∠BOC,若∠AOD=68°,则∠COE的度数是( )
A.32°
B.34°
C.36°
D.38°
5.如图,直线AB,CD相交于点O,因为∠1+∠3=180°,∠2+∠3=180°,所以∠1=∠2,其推理依据为( )
A.对顶角相等
B.同角的余角相等
C.等量代换
D.同角的补角相等
6.如图,直线AB,CD相交于点O,OE,OF为射线,则图中的对顶角有( )
A.1对
B.2对
C.3对
D.4对
7.[2020·东营]如图,直线AB,CD相交于点O,射线OM平分∠BOD,若∠AOC=42°,则∠AOM等于 ( )
A.159°
B.161°
C.169°
D.138°
二、填空题
8.(2021江西九江期末模拟)如图,直线a,b相交,∠1+∠2=58°,则∠3的大小为 .
9.如图,直线AB,CD相交于点O,∠EOB=90°,∠COB=145°,则∠DOE= .
10.(2021黑龙江大庆中考)如图,3条直线两两相交最多有3个交点,4条直线两两相交最多有6个交点,按照这样的规律,则20条直线两两相交最多有 个交点.
11.如图 ,直线AB,CD,MN相交于点O,则∠AOD的对顶角是________,∠COM的邻补角是____________.若∠AOC=50°,则∠BOD=________,∠COB=________.
12. 填空:
(1)两条直线相交于一点,有________对对顶角;
(2)三条直线相交于一点,有________对对顶角;
(3)四条直线相交于一点,有________对对顶角;
(4)n条直线相交于一点,有________对对顶角.
三、解答题
13.(2021湖南长沙天心明德教育集团第一次月考)如图,两条直线a,b相交.
(1)如果∠1=50°,求∠2,∠3的度数;
(2)如果∠2=3∠1,求∠3,∠4的度数.
14.(2021河南商丘柘城期末)如图,直线AB,CD相交于点O,OA平分∠EOC.
(1)若∠EOC=70°,求∠BOD的度数;
(2)若∠EOC∶∠EOD=2∶3,求∠BOD的度数.
15.如图,直线AB、CD相交于O,OD平分∠AOF,∠EOD=90°,∠1=50°,求∠COB、∠BOF的度数.
一、选择题
1.答案 A 选项B、C、D中的∠1和∠2的两边都不是互为反向延长线,所以不是对顶角;只有选项A符合题意,故选A.
2.答案 B ∵将剪刀的两边抽象为两条直线AB与CD,∠1=35°,
∴∠2=∠1=35°.故选B.
3.答案 D 根据邻补角的定义可知,只有D选项中的∠1与∠2互为邻补角.
4.答案 B ∵∠BOC与∠AOD互为对顶角,∴∠BOC=∠AOD,
∵∠AOD=68°,∴∠BOC=68°,
∵OE平分∠BOC,∴∠COE=∠BOC=×68°=34°.故选B.
5.答案 D
6. 答案 B
7. 答案 A
二、填空题
8.答案 151°
解析 ∵∠1+∠2=58°,∠1=∠2(对顶角相等),∴∠1=×58°=29°,
∴∠3=180°-∠1=180°-29°=151°.故答案为151°.
9.答案 55°
解析 ∵∠COB=145°,∴∠DOB=35°,∵∠EOB=90°,∴∠DOE=90°-35°=55°.
10.答案 190
解析 2条直线相交有1个交点,
3条直线两两相交最多有1+2=3个交点,
4条直线两两相交最多有1+2+3=6个交点,……
n条直线两两相交最多有个交点,
∴20条直线两两相交最多有190个交点.
故答案为190.
11. 答案 ∠BOC ∠CON,∠MOD 50° 130°
12. 答案 (1)2 (2)6 (3)12 (4)n(n-1)
三、解答题
13.解析 (1)∵∠1=50°,∠1+∠2=180°,
∴∠2=180°-50°=130°.
∵∠3与∠1是对顶角,∴∠3=∠1=50°.
(2)∵∠2=3∠1,∠1+∠2=180°,
∴∠1+3∠1=180°,∴4∠1=180°,
∴∠1=45°,∴∠3=∠1=45°.
∵∠1+∠4=180°,
∴∠4=180°-∠1=180°-45°=135°.
14.解析 (1)∵OA平分∠EOC,∴∠AOC=∠EOC=×70°=35°,
∴∠BOD=∠AOC=35°.
(2)设∠EOC=2x,∠EOD=3x,根据题意得2x+3x=180°,解得x=36°,
∴∠EOC=2x=72°,∴∠AOC=∠EOC=×72°=36°,
∴∠BOD=∠AOC=36°.
15.解析 ∵∠EOD=90°,∠1=50°,∴∠AOD=90°-∠1=40°,
∵∠BOC与∠AOD是对顶角,∴∠BOC=∠AOD=40°.
∵OD平分∠AOF,∴∠DOF=∠AOD=40°,
∴∠BOF=180°-∠BOC-∠DOF=180°-40°-40°=100°.
1
班级 姓名
第五章 相交线与平行线
5.1 相交线
5.1.1 相交线
一、选择题
1.(2021安徽合肥巢湖期末)如图所示,∠1和∠2是对顶角的是( )
2.如图,我们将剪刀的两边抽象为两条直线AB与CD,它们相交于点O,若∠1=35°,则∠2=( )
A.30°
B.35°
C.40°
D.45°
3.(2021湖北荆门期末)下列选项中,∠1与∠2互为邻补角的是( )
4.(2021安徽马鞍山当涂期末)如图,直线AB、CD相交于点O,OE平分∠BOC,若∠AOD=68°,则∠COE的度数是( )
A.32°
B.34°
C.36°
D.38°
5.如图,直线AB,CD相交于点O,因为∠1+∠3=180°,∠2+∠3=180°,所以∠1=∠2,其推理依据为( )
A.对顶角相等
B.同角的余角相等
C.等量代换
D.同角的补角相等
6.如图,直线AB,CD相交于点O,OE,OF为射线,则图中的对顶角有( )
A.1对
B.2对
C.3对
D.4对
7.[2020·东营]如图,直线AB,CD相交于点O,射线OM平分∠BOD,若∠AOC=42°,则∠AOM等于 ( )
A.159°
B.161°
C.169°
D.138°
二、填空题
8.(2021江西九江期末模拟)如图,直线a,b相交,∠1+∠2=58°,则∠3的大小为 .
9.如图,直线AB,CD相交于点O,∠EOB=90°,∠COB=145°,则∠DOE= .
10.(2021黑龙江大庆中考)如图,3条直线两两相交最多有3个交点,4条直线两两相交最多有6个交点,按照这样的规律,则20条直线两两相交最多有 个交点.
11.如图 ,直线AB,CD,MN相交于点O,则∠AOD的对顶角是________,∠COM的邻补角是____________.若∠AOC=50°,则∠BOD=________,∠COB=________.
12. 填空:
(1)两条直线相交于一点,有________对对顶角;
(2)三条直线相交于一点,有________对对顶角;
(3)四条直线相交于一点,有________对对顶角;
(4)n条直线相交于一点,有________对对顶角.
三、解答题
13.(2021湖南长沙天心明德教育集团第一次月考)如图,两条直线a,b相交.
(1)如果∠1=50°,求∠2,∠3的度数;
(2)如果∠2=3∠1,求∠3,∠4的度数.
14.(2021河南商丘柘城期末)如图,直线AB,CD相交于点O,OA平分∠EOC.
(1)若∠EOC=70°,求∠BOD的度数;
(2)若∠EOC∶∠EOD=2∶3,求∠BOD的度数.
15.如图,直线AB、CD相交于O,OD平分∠AOF,∠EOD=90°,∠1=50°,求∠COB、∠BOF的度数.
一、选择题
1.答案 A 选项B、C、D中的∠1和∠2的两边都不是互为反向延长线,所以不是对顶角;只有选项A符合题意,故选A.
2.答案 B ∵将剪刀的两边抽象为两条直线AB与CD,∠1=35°,
∴∠2=∠1=35°.故选B.
3.答案 D 根据邻补角的定义可知,只有D选项中的∠1与∠2互为邻补角.
4.答案 B ∵∠BOC与∠AOD互为对顶角,∴∠BOC=∠AOD,
∵∠AOD=68°,∴∠BOC=68°,
∵OE平分∠BOC,∴∠COE=∠BOC=×68°=34°.故选B.
5.答案 D
6. 答案 B
7. 答案 A
二、填空题
8.答案 151°
解析 ∵∠1+∠2=58°,∠1=∠2(对顶角相等),∴∠1=×58°=29°,
∴∠3=180°-∠1=180°-29°=151°.故答案为151°.
9.答案 55°
解析 ∵∠COB=145°,∴∠DOB=35°,∵∠EOB=90°,∴∠DOE=90°-35°=55°.
10.答案 190
解析 2条直线相交有1个交点,
3条直线两两相交最多有1+2=3个交点,
4条直线两两相交最多有1+2+3=6个交点,……
n条直线两两相交最多有个交点,
∴20条直线两两相交最多有190个交点.
故答案为190.
11. 答案 ∠BOC ∠CON,∠MOD 50° 130°
12. 答案 (1)2 (2)6 (3)12 (4)n(n-1)
三、解答题
13.解析 (1)∵∠1=50°,∠1+∠2=180°,
∴∠2=180°-50°=130°.
∵∠3与∠1是对顶角,∴∠3=∠1=50°.
(2)∵∠2=3∠1,∠1+∠2=180°,
∴∠1+3∠1=180°,∴4∠1=180°,
∴∠1=45°,∴∠3=∠1=45°.
∵∠1+∠4=180°,
∴∠4=180°-∠1=180°-45°=135°.
14.解析 (1)∵OA平分∠EOC,∴∠AOC=∠EOC=×70°=35°,
∴∠BOD=∠AOC=35°.
(2)设∠EOC=2x,∠EOD=3x,根据题意得2x+3x=180°,解得x=36°,
∴∠EOC=2x=72°,∴∠AOC=∠EOC=×72°=36°,
∴∠BOD=∠AOC=36°.
15.解析 ∵∠EOD=90°,∠1=50°,∴∠AOD=90°-∠1=40°,
∵∠BOC与∠AOD是对顶角,∴∠BOC=∠AOD=40°.
∵OD平分∠AOF,∴∠DOF=∠AOD=40°,
∴∠BOF=180°-∠BOC-∠DOF=180°-40°-40°=100°.
1
