广东省湛江市2013届高三10月调研测试数学文试题
文档属性
| 名称 | 广东省湛江市2013届高三10月调研测试数学文试题 |  | |
| 格式 | zip | ||
| 文件大小 | 3.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标B版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2012-10-29 21:36:37 | ||
图片预览


文档简介
广东省湛江市2013届高中毕业班调研测试
数学(文)试题
本试卷共4页,共21小题,满分150分。考试用时120分钟。
注意事项:
1.答卷前,考生务必用黑色字迹的钢笔或签字笔将自己的姓名和考生号填在答题卡上。用2B铅笔将答题卡试卷类型(A)填涂在答题卡上。在答题卡右上角的"试室号"和"座位号"栏填写试室号、座位号,将相应的试室号、座位号信息点涂黑。
2.选择题每小题选出答案后,用2B铅笔把答题卡上对应题目的答案标号涂黑;如需改动,用橡皮擦干净后,再选涂其它答案,不能答在试卷上。
3.非选择题必须用黑色字迹钢笔或签字笔作答,答案必须写在答题卡各题目指定区域内相应位置上;如需改动,先划掉原来的答案,然后再写上新的答案;不准使用铅笔和涂改液。不按以上求作答的答案无效。
4.考试结束后,将试卷和答题卡一并交回。
参考公式:
锥体的体积公式:V=·S·h,其中S是底面积,h是高。
一组数据x1,x2,…,xn的方差…+,其中为…的平均数。
一、选择题:本大题共10小题,每小题5分,共50分。在每小题给出的四个选项中,只有一项是符合题目要求的。
1.已知i是虚数单位,则复数 ( )
A.-1-i B.-1+i C.1+i D.1-i
2.函数是 ( )
A.奇函数 B.偶函数
C.既是奇函数又是偶函数 D.既不是奇函数也不是偶函数
3.设集合 ( )
A. B.
C. D.
4.已知函数,若,则a= ( )
A.4 B.2 C.1 D.-1
5.已知等差数列的前n项和为Sn,若 ( )
A.18 B.36 C.54 D.72
6.曲线在x=1处的切线方程为 ( )
A.y=x B.y=x-1
C.y=x+1 D.y=-x+1
7.已知m,则“m>2”是“方程
表示双椭圆”的 ( )
A.充分不必要条件
B.必要不充分条件
C.充要条件
D.既不充分也不必要条件
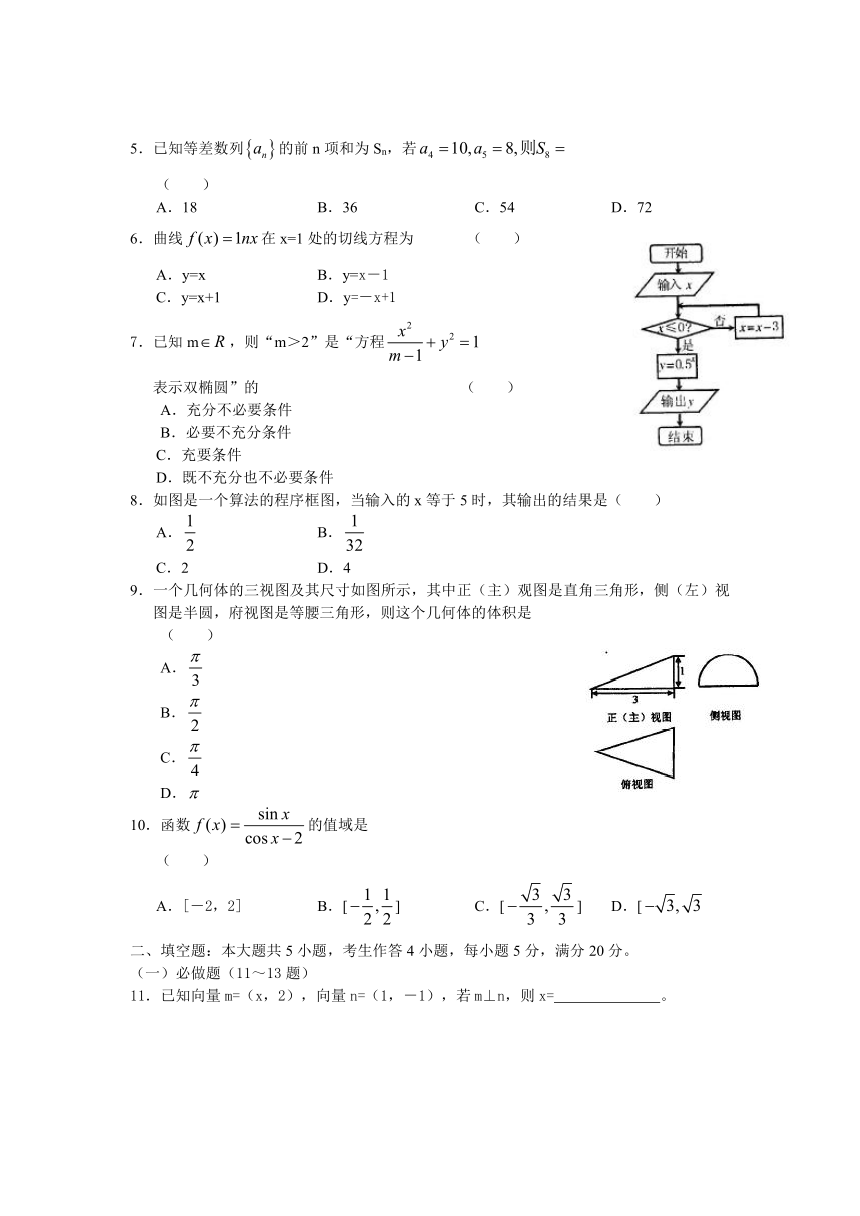
8.如图是一个算法的程序框图,当输入的x等于5时,其输出的结果是( )
A. B.
C.2 D.4
9.一个几何体的三视图及其尺寸如图所示,其中正(主)观图是直角三角形,侧(左)视图是半圆,府视图是等腰三角形,则这个几何体的体积是 ( )
A.
B.
C.
D.
10.函数的值域是 ( )
A.[-2,2] B.[] C.[] D.[
二、填空题:本大题共5小题,考生作答4小题,每小题5分,满分20分。
(一)必做题(11~13题)
11.已知向量m=(x,2),向量n=(1,-1),若 m⊥n,则x= 。
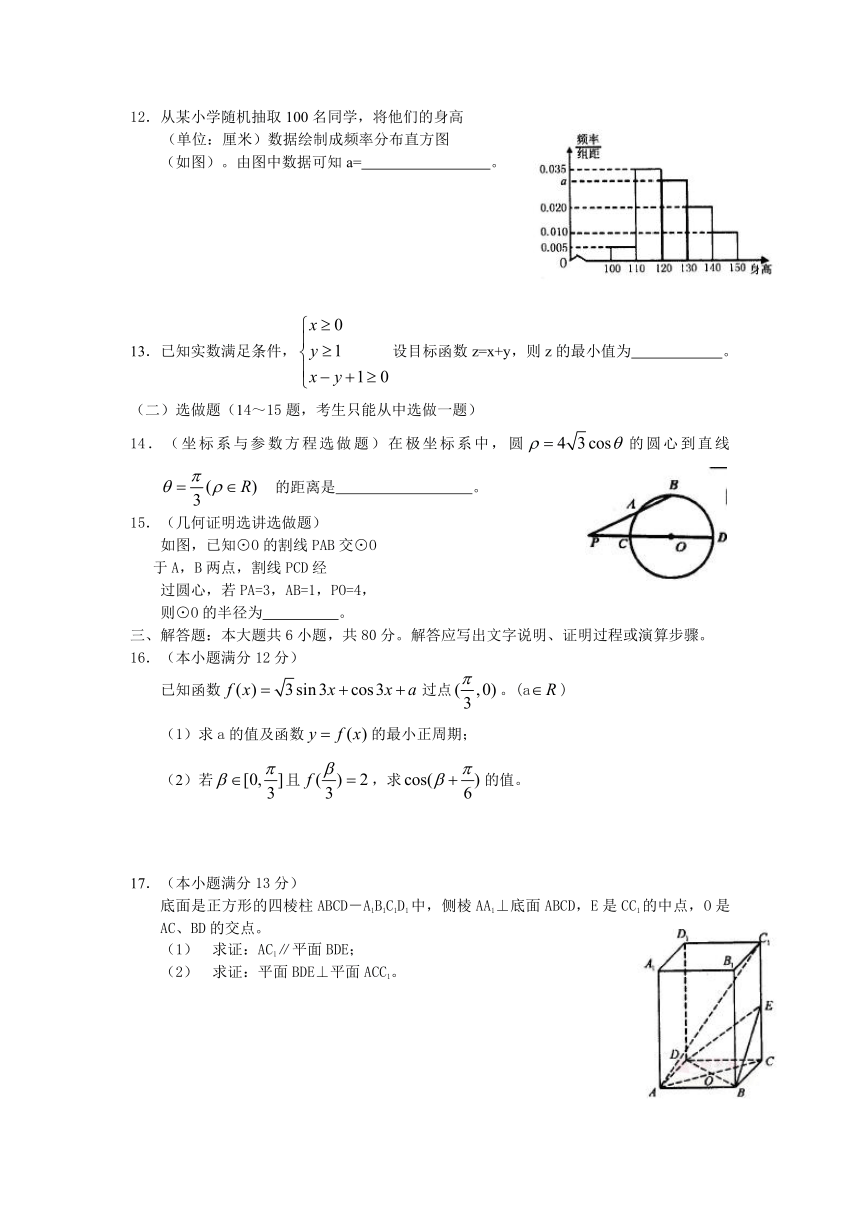
12.从某小学随机抽取100名同学,将他们的身高
(单位:厘米)数据绘制成频率分布直方图
(如图)。由图中数据可知a= 。
13.已知实数满足条件,设目标函数z=x+y,则z的最小值为 。
(二)选做题(14~15题,考生只能从中选做一题)
14.(坐标系与参数方程选做题)在极坐标系中,圆的圆心到直线 的距离是 。
15.(几何证明选讲选做题)
如图,已知⊙O的割线PAB交⊙O
于A,B两点,割线PCD经
过圆心,若PA=3,AB=1,PO=4,
则⊙O的半径为 。
三、解答题:本大题共6小题,共80分。解答应写出文字说明、证明过程或演算步骤。
16.(本小题满分12分)
已知函数过点。(a)
(1)求a的值及函数的最小正周期;
(2)若且,求的值。
17.(本小题满分13分)
底面是正方形的四棱柱ABCD-A1B1C1D1中,侧棱AA1⊥底面ABCD,E是CC1的中点,O是AC、BD的交点。
求证:AC1∥平面BDE;
求证:平面BDE⊥平面ACC1。
18.(本小题满分13分)
以下茎叶图记录了甲、乙两组各四名同学的投篮命中次数,乙组记录中有一个数据模糊,无法确认,在图中以X表示。
如果乙组同学投篮命中次数的平均数为,求X及乙组同学投篮命中次数的方差;
如果X=9,分别从甲、乙两组中随机选取一名同学,求这两名同学的投篮命中次数之和为19的概率。
19.(本小题满分14分)
已知等差数列的公差为,等比数列的公比为
求数列与的通项公式;
若cn=an·bn,求数列的前n项和Sn。
20.(本小题满分14分)
已知抛物线的焦点为F,A是抛物线上横坐标为4、且位于x轴上方的点,A到抛物线准线的距离等于5,过A作AB垂直于y轴,垂足为B,OB的中点为M。
(1)求抛物线方程;
(2)过M作MN⊥FA,垂足为N,求点N的坐标;
(3)以M为圆心,MB为半径作⊙M,当K(m,0)是x轴上一动点时,讨论直线AK与⊙M的位置关系。
21.(本小题满分14分)
已知函数的图象由函数·向左平移1个单位得到。
(1)求函数的表达式;
(2)当a=1时,求函数的最小值;
(3)若函数的最小值是m,且m>,求实数a的取值范围
数学(文)试题
本试卷共4页,共21小题,满分150分。考试用时120分钟。
注意事项:
1.答卷前,考生务必用黑色字迹的钢笔或签字笔将自己的姓名和考生号填在答题卡上。用2B铅笔将答题卡试卷类型(A)填涂在答题卡上。在答题卡右上角的"试室号"和"座位号"栏填写试室号、座位号,将相应的试室号、座位号信息点涂黑。
2.选择题每小题选出答案后,用2B铅笔把答题卡上对应题目的答案标号涂黑;如需改动,用橡皮擦干净后,再选涂其它答案,不能答在试卷上。
3.非选择题必须用黑色字迹钢笔或签字笔作答,答案必须写在答题卡各题目指定区域内相应位置上;如需改动,先划掉原来的答案,然后再写上新的答案;不准使用铅笔和涂改液。不按以上求作答的答案无效。
4.考试结束后,将试卷和答题卡一并交回。
参考公式:
锥体的体积公式:V=·S·h,其中S是底面积,h是高。
一组数据x1,x2,…,xn的方差…+,其中为…的平均数。
一、选择题:本大题共10小题,每小题5分,共50分。在每小题给出的四个选项中,只有一项是符合题目要求的。
1.已知i是虚数单位,则复数 ( )
A.-1-i B.-1+i C.1+i D.1-i
2.函数是 ( )
A.奇函数 B.偶函数
C.既是奇函数又是偶函数 D.既不是奇函数也不是偶函数
3.设集合 ( )
A. B.
C. D.
4.已知函数,若,则a= ( )
A.4 B.2 C.1 D.-1
5.已知等差数列的前n项和为Sn,若 ( )
A.18 B.36 C.54 D.72
6.曲线在x=1处的切线方程为 ( )
A.y=x B.y=x-1
C.y=x+1 D.y=-x+1
7.已知m,则“m>2”是“方程
表示双椭圆”的 ( )
A.充分不必要条件
B.必要不充分条件
C.充要条件
D.既不充分也不必要条件
8.如图是一个算法的程序框图,当输入的x等于5时,其输出的结果是( )
A. B.
C.2 D.4
9.一个几何体的三视图及其尺寸如图所示,其中正(主)观图是直角三角形,侧(左)视图是半圆,府视图是等腰三角形,则这个几何体的体积是 ( )
A.
B.
C.
D.
10.函数的值域是 ( )
A.[-2,2] B.[] C.[] D.[
二、填空题:本大题共5小题,考生作答4小题,每小题5分,满分20分。
(一)必做题(11~13题)
11.已知向量m=(x,2),向量n=(1,-1),若 m⊥n,则x= 。
12.从某小学随机抽取100名同学,将他们的身高
(单位:厘米)数据绘制成频率分布直方图
(如图)。由图中数据可知a= 。
13.已知实数满足条件,设目标函数z=x+y,则z的最小值为 。
(二)选做题(14~15题,考生只能从中选做一题)
14.(坐标系与参数方程选做题)在极坐标系中,圆的圆心到直线 的距离是 。
15.(几何证明选讲选做题)
如图,已知⊙O的割线PAB交⊙O
于A,B两点,割线PCD经
过圆心,若PA=3,AB=1,PO=4,
则⊙O的半径为 。
三、解答题:本大题共6小题,共80分。解答应写出文字说明、证明过程或演算步骤。
16.(本小题满分12分)
已知函数过点。(a)
(1)求a的值及函数的最小正周期;
(2)若且,求的值。
17.(本小题满分13分)
底面是正方形的四棱柱ABCD-A1B1C1D1中,侧棱AA1⊥底面ABCD,E是CC1的中点,O是AC、BD的交点。
求证:AC1∥平面BDE;
求证:平面BDE⊥平面ACC1。
18.(本小题满分13分)
以下茎叶图记录了甲、乙两组各四名同学的投篮命中次数,乙组记录中有一个数据模糊,无法确认,在图中以X表示。
如果乙组同学投篮命中次数的平均数为,求X及乙组同学投篮命中次数的方差;
如果X=9,分别从甲、乙两组中随机选取一名同学,求这两名同学的投篮命中次数之和为19的概率。
19.(本小题满分14分)
已知等差数列的公差为,等比数列的公比为
求数列与的通项公式;
若cn=an·bn,求数列的前n项和Sn。
20.(本小题满分14分)
已知抛物线的焦点为F,A是抛物线上横坐标为4、且位于x轴上方的点,A到抛物线准线的距离等于5,过A作AB垂直于y轴,垂足为B,OB的中点为M。
(1)求抛物线方程;
(2)过M作MN⊥FA,垂足为N,求点N的坐标;
(3)以M为圆心,MB为半径作⊙M,当K(m,0)是x轴上一动点时,讨论直线AK与⊙M的位置关系。
21.(本小题满分14分)
已知函数的图象由函数·向左平移1个单位得到。
(1)求函数的表达式;
(2)当a=1时,求函数的最小值;
(3)若函数的最小值是m,且m>,求实数a的取值范围
同课章节目录
