2021—2022学年人教版七年级数学下册5.2.1 平行线 同步训练 (Word版含简答)
文档属性
| 名称 | 2021—2022学年人教版七年级数学下册5.2.1 平行线 同步训练 (Word版含简答) |

|
|
| 格式 | doc | ||
| 文件大小 | 109.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-12-27 00:00:00 | ||
图片预览



文档简介
2022年春人教版初中七年级数学下册 同步训练
班级 姓名
第五章 相交线与平行线
5.2 平行线及其判定
5.2.1 平行线
测试时间:10分钟
一、选择题
1.(2021河北秦皇岛青龙期末)在同一平面内,不重合的两条直线的位置关系是( )
A.平行 B.相交
C.平行或相交 D.平行、相交或垂直
2.已知∠AOB,P是任一点,过点P画一条直线与OA平行,则这样的直线( )
A.有且仅有一条 B.有两条
C.不存在 D.有一条或不存在
3. 若M,N是直线AB外不重合的两点,下列说法不正确的是( )
A.直线MN可能与直线AB平行
B.直线MN可能与直线AB垂直
C.过点M能作一条直线与直线AB平行
D.过点N的直线一定能与直线AB相交
4.下列说法不正确的是( )
A.过任意一点可作已知直线的一条平行线
B.同一平面内两条不相交的直线是平行线
C.在同一平面内,过直线外一点只能画一条直线与已知直线垂直
D.平行于同一直线的两条直线平行
5. 下列说法中正确的个数有( )
①经过一点有且只有一条直线与已知直线垂直;
②经过直线外一点,有且只有一条直线与已知直线平行;
③连接直线外一点与直线上各点的所有线段中,垂线段最短;
④两条直线相交,对顶角相等.
A.1个 B.2个
C.3个 D.4个
二、填空题
6.在同一平面内,若a⊥b,b⊥c,则a与c的位置关系是 .
7.如图,AB∥l,AC∥l,则A,B,C三点共线,理由是: .
8.下列各说法中,错误的是 (填序号).
①过一点有且只有一条直线与已知直线平行;
②在同一平面内,两条不相交的线段是平行线段;
③两条直线没有交点,则这两条直线平行;
④在同一平面内,若直线AB∥CD,直线AB与EF相交,则直线CD与EF相交.
9.工人师傅在铺设地下管线时,为检验三条同一平面上的管线是否平行,工人师傅只检验其中两条是否与第三条平行即可,这种检验方法的依据是 .
10.如图 ,将一张长方形的硬纸片ABCD对折,MN是折痕,把面ABNM平摊在桌面上,另一个面CDMN不论怎样改变位置,总有MN∥________,MN∥________,因此________∥________.
11.两个相同的含30°,60°,90°角的三角尺,最多可以拼出________组不同的平行线.
12.如图 ,根据要求填空:
(1)过点A作AE∥BC,交________于点E;
(2)过点B作BF∥AD,交________于点F;
(3)过点D作DH∥BC,交BA的________于点H;
(4)过点C作CG∥AD,交_____________________.
三、解答题
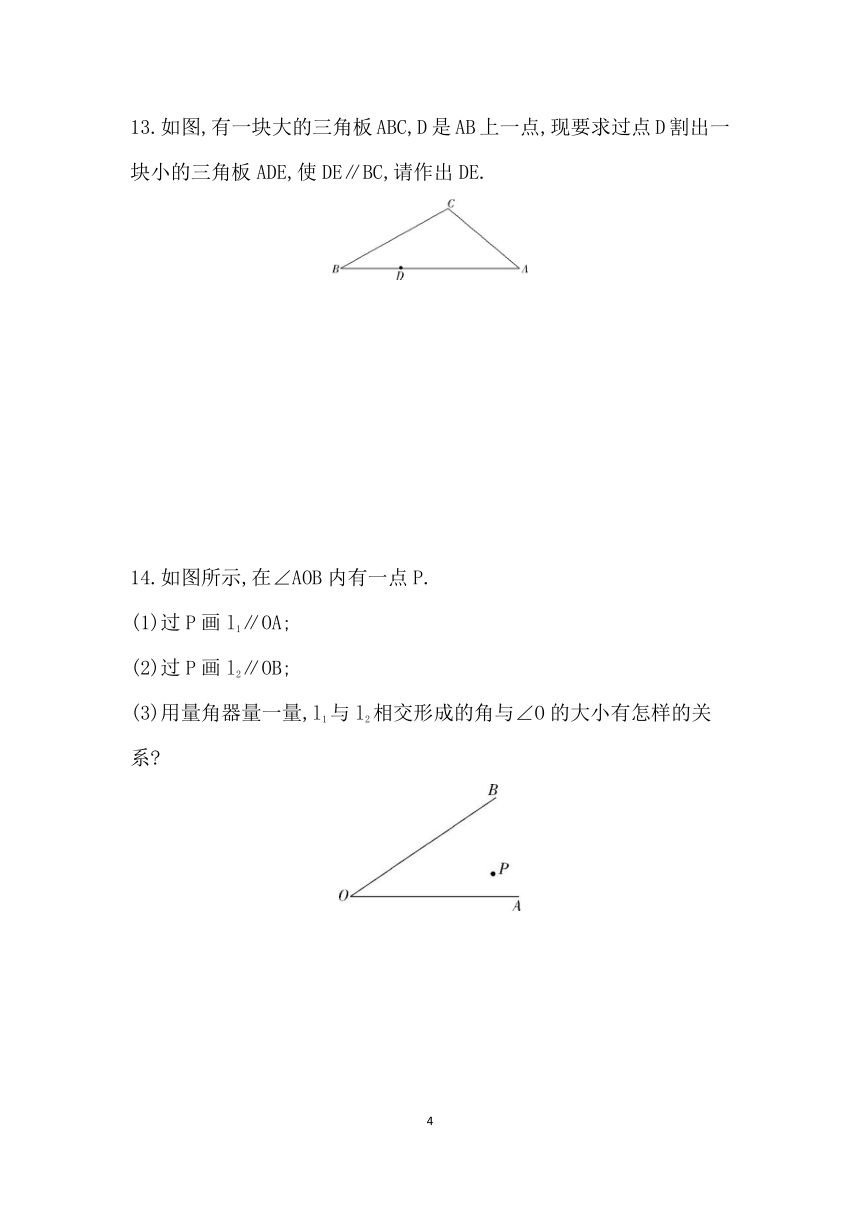
13.如图,有一块大的三角板ABC,D是AB上一点,现要求过点D割出一块小的三角板ADE,使DE∥BC,请作出DE.
14.如图所示,在∠AOB内有一点P.
(1)过P画l1∥OA;
(2)过P画l2∥OB;
(3)用量角器量一量,l1与l2相交形成的角与∠O的大小有怎样的关系
15.如图 .
(1)过点D画直线DE∥BC,交AC于点E,再过点E画EF∥AB,交BC于点F;
(2)分别量出∠B,∠BDE,∠DEF,∠EFC的度数,你有什么发现?
一、选择题
1.答案 C 在同一平面内,不重合的两条直线只有两种位置关系:平行和相交,故选C.
2.答案 D ①若点P在直线OA上,则过点P不能画出与OA平行的直线;②若点P不在直线OA上,则过点P有且只有一条直线与OA平行,所以这样的直线有一条或不存在.故选D.
3.答案 D 直线MN与直线AB可能平行,也可能垂直,过直线外一点有且只有一条直线与已知直线平行,故A、B、C说法均正确,选项D说法错误.故选D.
4. 答案 A
5. 答案 C
二、填空题
6.答案 a∥c
解析 根据在同一平面内,垂直于同一条直线的两条直线互相平行即可求解.
∵a⊥b,b⊥c,∴a∥c.
7.答案 经过直线外一点,有且只有一条直线与已知直线平行
解析 ∵AB∥l,AC∥l,
∴A,B,C三点共线(经过直线外一点,有且只有一条直线与已知直线平行).
8.答案 ①②③
解析 ①过直线外一点,有且只有一条直线与已知直线平行,原说法错误;
②在同一平面内,两条不相交的线段不一定是平行线段,原说法错误;
③没有说明在同一平面内,故原说法错误;
④在同一平面内,若直线AB∥CD,直线AB与EF相交,则直线CD与EF相交,说法正确.
故说法错误的是①②③.
9.答案 平行于同一条直线的两条直线平行
10. 答案 AB CD AB CD
11. 答案 3
12.答案 (1)DC (2)DC (3)延长线
(4)AB的延长线于点G
三、解答题
13.解析 如图.
14.解析 (1)(2)如图所示.
(3)如图,∠1=∠O,∠2+∠O=180°,所以l1和l2相交形成的角与∠O相等或互补.
15.解:(1)如答图.
(2)量出∠B=45°,∠BDE=135°,∠DEF=45°,∠EFC=45°,可以发现∠B=∠DEF=∠EFC,∠BDE+∠B=180°.
1
班级 姓名
第五章 相交线与平行线
5.2 平行线及其判定
5.2.1 平行线
测试时间:10分钟
一、选择题
1.(2021河北秦皇岛青龙期末)在同一平面内,不重合的两条直线的位置关系是( )
A.平行 B.相交
C.平行或相交 D.平行、相交或垂直
2.已知∠AOB,P是任一点,过点P画一条直线与OA平行,则这样的直线( )
A.有且仅有一条 B.有两条
C.不存在 D.有一条或不存在
3. 若M,N是直线AB外不重合的两点,下列说法不正确的是( )
A.直线MN可能与直线AB平行
B.直线MN可能与直线AB垂直
C.过点M能作一条直线与直线AB平行
D.过点N的直线一定能与直线AB相交
4.下列说法不正确的是( )
A.过任意一点可作已知直线的一条平行线
B.同一平面内两条不相交的直线是平行线
C.在同一平面内,过直线外一点只能画一条直线与已知直线垂直
D.平行于同一直线的两条直线平行
5. 下列说法中正确的个数有( )
①经过一点有且只有一条直线与已知直线垂直;
②经过直线外一点,有且只有一条直线与已知直线平行;
③连接直线外一点与直线上各点的所有线段中,垂线段最短;
④两条直线相交,对顶角相等.
A.1个 B.2个
C.3个 D.4个
二、填空题
6.在同一平面内,若a⊥b,b⊥c,则a与c的位置关系是 .
7.如图,AB∥l,AC∥l,则A,B,C三点共线,理由是: .
8.下列各说法中,错误的是 (填序号).
①过一点有且只有一条直线与已知直线平行;
②在同一平面内,两条不相交的线段是平行线段;
③两条直线没有交点,则这两条直线平行;
④在同一平面内,若直线AB∥CD,直线AB与EF相交,则直线CD与EF相交.
9.工人师傅在铺设地下管线时,为检验三条同一平面上的管线是否平行,工人师傅只检验其中两条是否与第三条平行即可,这种检验方法的依据是 .
10.如图 ,将一张长方形的硬纸片ABCD对折,MN是折痕,把面ABNM平摊在桌面上,另一个面CDMN不论怎样改变位置,总有MN∥________,MN∥________,因此________∥________.
11.两个相同的含30°,60°,90°角的三角尺,最多可以拼出________组不同的平行线.
12.如图 ,根据要求填空:
(1)过点A作AE∥BC,交________于点E;
(2)过点B作BF∥AD,交________于点F;
(3)过点D作DH∥BC,交BA的________于点H;
(4)过点C作CG∥AD,交_____________________.
三、解答题
13.如图,有一块大的三角板ABC,D是AB上一点,现要求过点D割出一块小的三角板ADE,使DE∥BC,请作出DE.
14.如图所示,在∠AOB内有一点P.
(1)过P画l1∥OA;
(2)过P画l2∥OB;
(3)用量角器量一量,l1与l2相交形成的角与∠O的大小有怎样的关系
15.如图 .
(1)过点D画直线DE∥BC,交AC于点E,再过点E画EF∥AB,交BC于点F;
(2)分别量出∠B,∠BDE,∠DEF,∠EFC的度数,你有什么发现?
一、选择题
1.答案 C 在同一平面内,不重合的两条直线只有两种位置关系:平行和相交,故选C.
2.答案 D ①若点P在直线OA上,则过点P不能画出与OA平行的直线;②若点P不在直线OA上,则过点P有且只有一条直线与OA平行,所以这样的直线有一条或不存在.故选D.
3.答案 D 直线MN与直线AB可能平行,也可能垂直,过直线外一点有且只有一条直线与已知直线平行,故A、B、C说法均正确,选项D说法错误.故选D.
4. 答案 A
5. 答案 C
二、填空题
6.答案 a∥c
解析 根据在同一平面内,垂直于同一条直线的两条直线互相平行即可求解.
∵a⊥b,b⊥c,∴a∥c.
7.答案 经过直线外一点,有且只有一条直线与已知直线平行
解析 ∵AB∥l,AC∥l,
∴A,B,C三点共线(经过直线外一点,有且只有一条直线与已知直线平行).
8.答案 ①②③
解析 ①过直线外一点,有且只有一条直线与已知直线平行,原说法错误;
②在同一平面内,两条不相交的线段不一定是平行线段,原说法错误;
③没有说明在同一平面内,故原说法错误;
④在同一平面内,若直线AB∥CD,直线AB与EF相交,则直线CD与EF相交,说法正确.
故说法错误的是①②③.
9.答案 平行于同一条直线的两条直线平行
10. 答案 AB CD AB CD
11. 答案 3
12.答案 (1)DC (2)DC (3)延长线
(4)AB的延长线于点G
三、解答题
13.解析 如图.
14.解析 (1)(2)如图所示.
(3)如图,∠1=∠O,∠2+∠O=180°,所以l1和l2相交形成的角与∠O相等或互补.
15.解:(1)如答图.
(2)量出∠B=45°,∠BDE=135°,∠DEF=45°,∠EFC=45°,可以发现∠B=∠DEF=∠EFC,∠BDE+∠B=180°.
1
