2021—2022学年沪科版八年级数学下册19.2平行四边形的性质第2课时 同步练习(word版含答案)
文档属性
| 名称 | 2021—2022学年沪科版八年级数学下册19.2平行四边形的性质第2课时 同步练习(word版含答案) |
|
|
| 格式 | docx | ||
| 文件大小 | 150.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-12-28 00:00:00 | ||
图片预览


文档简介
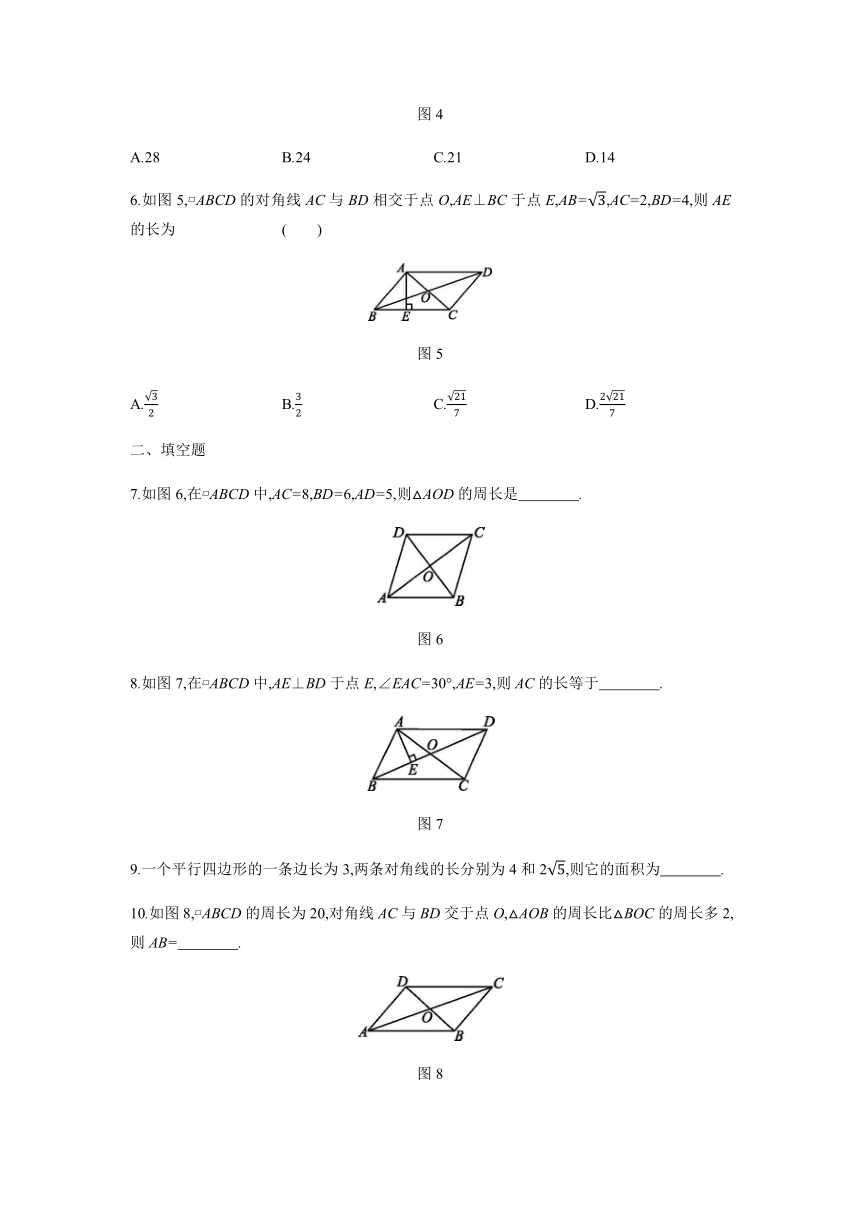
19.2 第2课时 平行四边形的性质3
一、选择题
1.平行四边形的对角线一定具有的性质是 ( )
A.相等 B.互相平分 C.互相垂直 D.互相垂直且相等
2.如图1所示,在 ABCD中,对角线AC,BD相交于点O,则下列结论中错误的是 ( )
图1
A.OA=OC B.AB=CD C.AC=BD D.∠ABC=∠ADC
3.如图2,在 ABCD中,对角线AC,BD相交于点O,AC=6,BD=10,则AD的长可以是 ( )
图2
A.2 B.7 C.8 D.10
4.如图3,在 ABCD中,AC,BD为对角线,BC=6,BC边上的高为4,则阴影部分的面积为 ( )
图3
A.3 B.6 C.12 D.24
5.如图4,在 ABCD中,对角线AC,BD相交于点O,OE⊥BD交AD于点E,连接BE,若 ABCD的周长为28,则△ABE的周长为 ( )
图4
A.28 B.24 C.21 D.14
6.如图5, ABCD的对角线AC与BD相交于点O,AE⊥BC于点E,AB=,AC=2,BD=4,则AE的长为 ( )
图5
A. B. C. D.
二、填空题
7.如图6,在 ABCD中,AC=8,BD=6,AD=5,则△AOD的周长是 .
图6
8.如图7,在 ABCD中,AE⊥BD于点E,∠EAC=30°,AE=3,则AC的长等于 .
图7
9.一个平行四边形的一条边长为3,两条对角线的长分别为4和2,则它的面积为 .
10.如图8, ABCD的周长为20,对角线AC与BD交于点O,△AOB的周长比△BOC的周长多2,则AB= .
图8
11.如图9,在 ABCD中,∠B=60°,AB=4,BC=5,P是对角线AC上任一点(点P不与点A,C重合),且PE∥BC交AB于点E,PF∥CD交AD于点F,则阴影部分的面积是 .
图9
三、解答题
12.如图10,已知 ABCD的对角线AC,BD相交于点O,AD=12,BD=10,AC=26.
(1)求△AOD的周长;
(2)求证:△AOD是直角三角形.
图10
13.如图11, ABCD的对角线AC,BD交于点O,AC⊥AB,AB=2,且AC∶BD=2∶3.
(1)求AC的长;
(2)求△AOD的面积.
图11
14.(1)如图12①,在 ABCD中,E是AB边的中点,O是对角线AC的中点,连接EO并延长交CD边于点F,求证:F是CD的中点;
(2)如图②,在 ABCD中,E是AB边的中点,仅用一把无刻度的直尺画出CD边的中点F.(保留作图痕迹,不写作法)
图12
15.在一次数学探究活动中,小强用两条直线把某个平行四边形分割成四部分,使含有一组对顶角的两个图形全等.
(1)根据小强的分割方法,你认为把平行四边形分割成满足以上全等关系的直线有
组;
(2)请你在如图13所示的三个平行四边形中画出满足小强分割方法的直线;
图13
(3)由上述实验操作过程,你发现所画的两条直线有什么规律
答案
1.B 2.C 3.B 4.B 5.D 6.D
7.12
8.4 .
9.4
10.6 .
11.5
12.解:(1)∵四边形ABCD是平行四边形,
∴对角线AC与BD相互平分,
∴OA=OC=AC,OB=OD=BD.
∵AC=26,BD=10,∴OA=13,OD=5.
又∵AD=12,∴△AOD的周长=5+12+13=30.
(2)证明:由(1)知OA=13,OD=5,AD=12.
∵122+52=132,
∴在△AOD中,AD2+OD2=OA2,
∴△AOD是直角三角形.
13.解:(1)∵AC∶BD=2∶3,
∴设AC=2x,则BD=3x.
∵四边形ABCD是平行四边形,
∴OA=AC=x,OB=BD=x.
∵AC⊥AB,
∴AB2+OA2=OB2,即(2)2+x2=x2,解得x=4(负值已舍去),
∴AC=8.
(2)∵S ABCD=AB·AC=2×8=16,
∴S△AOD=S ABCD=4.
14.解:(1)证明:∵在 ABCD中,AB=CD,AB∥CD,∴∠OAE=∠OCF.
∵O是对角线AC的中点,∴OA=OC.
在△AOE和△COF中,∵
∴△AOE≌△COF,∴AE=CF.
∵E是AB边的中点,∴AE=AB.
∵AB=CD,∴AE=CD,
∴CF=CD,∴F是CD的中点.
(2)如图,连接AC和BD交于点O,连接EO并延长交CD于点F,F即为CD的中点.
15.解:(1)无数
(2)答案不唯一,如图所示(O为平行四边形对角线的交点).
(3)这两条直线均过平行四边形的对角线的交点.
一、选择题
1.平行四边形的对角线一定具有的性质是 ( )
A.相等 B.互相平分 C.互相垂直 D.互相垂直且相等
2.如图1所示,在 ABCD中,对角线AC,BD相交于点O,则下列结论中错误的是 ( )
图1
A.OA=OC B.AB=CD C.AC=BD D.∠ABC=∠ADC
3.如图2,在 ABCD中,对角线AC,BD相交于点O,AC=6,BD=10,则AD的长可以是 ( )
图2
A.2 B.7 C.8 D.10
4.如图3,在 ABCD中,AC,BD为对角线,BC=6,BC边上的高为4,则阴影部分的面积为 ( )
图3
A.3 B.6 C.12 D.24
5.如图4,在 ABCD中,对角线AC,BD相交于点O,OE⊥BD交AD于点E,连接BE,若 ABCD的周长为28,则△ABE的周长为 ( )
图4
A.28 B.24 C.21 D.14
6.如图5, ABCD的对角线AC与BD相交于点O,AE⊥BC于点E,AB=,AC=2,BD=4,则AE的长为 ( )
图5
A. B. C. D.
二、填空题
7.如图6,在 ABCD中,AC=8,BD=6,AD=5,则△AOD的周长是 .
图6
8.如图7,在 ABCD中,AE⊥BD于点E,∠EAC=30°,AE=3,则AC的长等于 .
图7
9.一个平行四边形的一条边长为3,两条对角线的长分别为4和2,则它的面积为 .
10.如图8, ABCD的周长为20,对角线AC与BD交于点O,△AOB的周长比△BOC的周长多2,则AB= .
图8
11.如图9,在 ABCD中,∠B=60°,AB=4,BC=5,P是对角线AC上任一点(点P不与点A,C重合),且PE∥BC交AB于点E,PF∥CD交AD于点F,则阴影部分的面积是 .
图9
三、解答题
12.如图10,已知 ABCD的对角线AC,BD相交于点O,AD=12,BD=10,AC=26.
(1)求△AOD的周长;
(2)求证:△AOD是直角三角形.
图10
13.如图11, ABCD的对角线AC,BD交于点O,AC⊥AB,AB=2,且AC∶BD=2∶3.
(1)求AC的长;
(2)求△AOD的面积.
图11
14.(1)如图12①,在 ABCD中,E是AB边的中点,O是对角线AC的中点,连接EO并延长交CD边于点F,求证:F是CD的中点;
(2)如图②,在 ABCD中,E是AB边的中点,仅用一把无刻度的直尺画出CD边的中点F.(保留作图痕迹,不写作法)
图12
15.在一次数学探究活动中,小强用两条直线把某个平行四边形分割成四部分,使含有一组对顶角的两个图形全等.
(1)根据小强的分割方法,你认为把平行四边形分割成满足以上全等关系的直线有
组;
(2)请你在如图13所示的三个平行四边形中画出满足小强分割方法的直线;
图13
(3)由上述实验操作过程,你发现所画的两条直线有什么规律
答案
1.B 2.C 3.B 4.B 5.D 6.D
7.12
8.4 .
9.4
10.6 .
11.5
12.解:(1)∵四边形ABCD是平行四边形,
∴对角线AC与BD相互平分,
∴OA=OC=AC,OB=OD=BD.
∵AC=26,BD=10,∴OA=13,OD=5.
又∵AD=12,∴△AOD的周长=5+12+13=30.
(2)证明:由(1)知OA=13,OD=5,AD=12.
∵122+52=132,
∴在△AOD中,AD2+OD2=OA2,
∴△AOD是直角三角形.
13.解:(1)∵AC∶BD=2∶3,
∴设AC=2x,则BD=3x.
∵四边形ABCD是平行四边形,
∴OA=AC=x,OB=BD=x.
∵AC⊥AB,
∴AB2+OA2=OB2,即(2)2+x2=x2,解得x=4(负值已舍去),
∴AC=8.
(2)∵S ABCD=AB·AC=2×8=16,
∴S△AOD=S ABCD=4.
14.解:(1)证明:∵在 ABCD中,AB=CD,AB∥CD,∴∠OAE=∠OCF.
∵O是对角线AC的中点,∴OA=OC.
在△AOE和△COF中,∵
∴△AOE≌△COF,∴AE=CF.
∵E是AB边的中点,∴AE=AB.
∵AB=CD,∴AE=CD,
∴CF=CD,∴F是CD的中点.
(2)如图,连接AC和BD交于点O,连接EO并延长交CD于点F,F即为CD的中点.
15.解:(1)无数
(2)答案不唯一,如图所示(O为平行四边形对角线的交点).
(3)这两条直线均过平行四边形的对角线的交点.
