2021-2022学年沪科版数学九年级上册第22章 相似形 单元测试卷 (Word版含解析)
文档属性
| 名称 | 2021-2022学年沪科版数学九年级上册第22章 相似形 单元测试卷 (Word版含解析) |
|
|
| 格式 | doc | ||
| 文件大小 | 467.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-12-28 08:32:59 | ||
图片预览





文档简介
第22章 相似形单元综合测试卷
一.选择题
1.若=,则等于( )
A. B. C. D.
2.根据有关测定,当外界气温处于人体正常体温的黄金比值时,人体感到最舒适(人体正常体温约为37℃),这个气温大约为( )
A.23℃ B.28℃ C.30℃ D.37℃
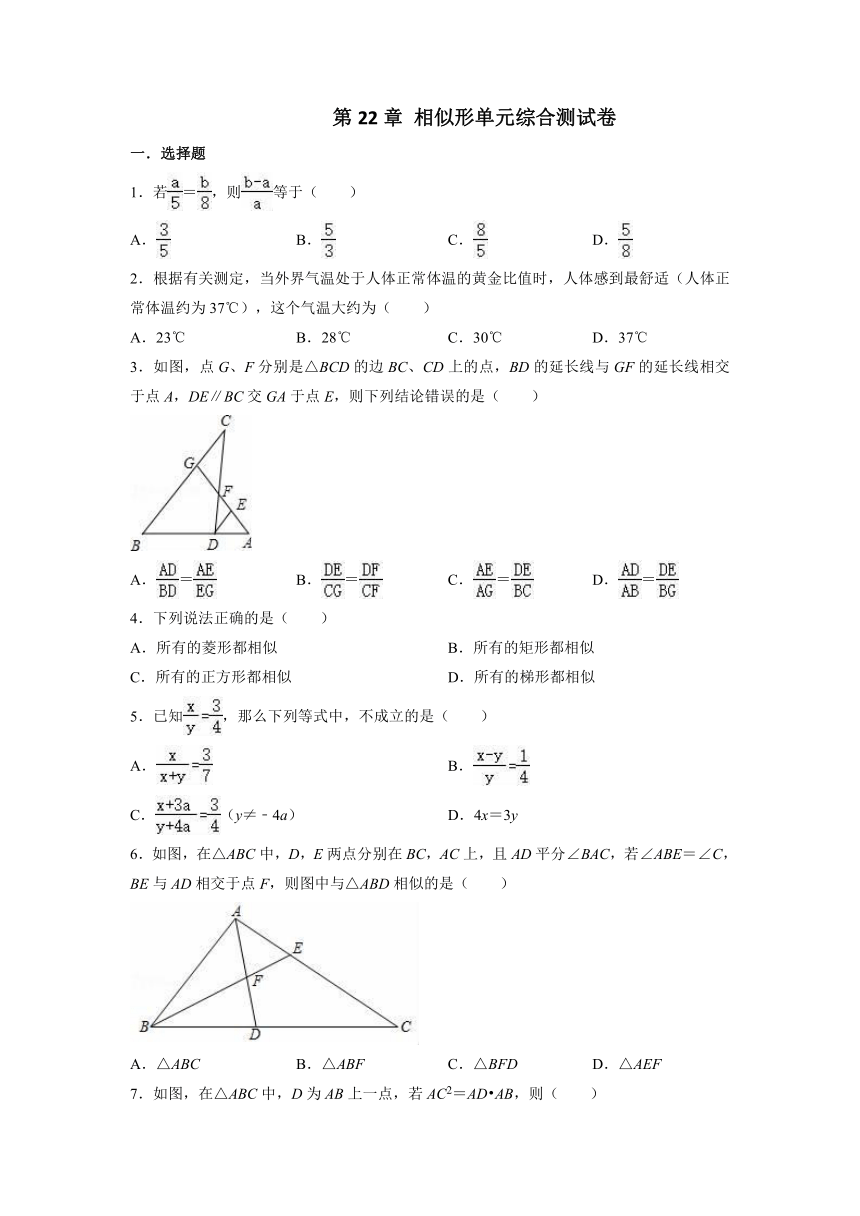
3.如图,点G、F分别是△BCD的边BC、CD上的点,BD的延长线与GF的延长线相交于点A,DE∥BC交GA于点E,则下列结论错误的是( )
A.= B.= C.= D.=
4.下列说法正确的是( )
A.所有的菱形都相似 B.所有的矩形都相似
C.所有的正方形都相似 D.所有的梯形都相似
5.已知,那么下列等式中,不成立的是( )
A. B.
C.(y≠﹣4a) D.4x=3y
6.如图,在△ABC中,D,E两点分别在BC,AC上,且AD平分∠BAC,若∠ABE=∠C,BE与AD相交于点F,则图中与△ABD相似的是( )
A.△ABC B.△ABF C.△BFD D.△AEF
7.如图,在△ABC中,D为AB上一点,若AC2=AD AB,则( )
A.△ADC∽△CBD B.△BDC∽△BCA C.△ADC∽△ACB D.无法判断
8.如图,在△ABC中,AD是中线,BC=8,∠B=∠DAC,则线段AC的长为( )
A.4 B.4 C.6 D.4
9.如图,在△ABC中,D,E分别是AB,BC上的点,且DE∥AC.若S△BDE∶S△CDE=1∶4,则S△BDE∶S△ADC等于( )
A.1∶16 B.1∶18 C.1∶20 D.1∶24
10.在△ABC中,AB=24,AC=18,D是AC上一点,AD=12,在AB上取一点E,使以A,D,E三点为顶点的三角形与△ABC相似,则AE的长为( )
A.16 B.14
C.16或14 D.16或9
二.填空题
11.若=,则= .
12.已知:,则= .
13.已知线段AB=10cm,点P是线段AB的黄金分割点,且AP>PB,则AP≈ cm.
14.如图,D,E分别是△ABC边AB,AC上的点,DE∥BC,AD=5,BD=3,BC=4,则DE长为 .
15.已知线段AB,点P是线段AB的黄金分割点,AP>BP,设以AP为边的正方形的面积为S1,以PB、AB为边的矩形的面积为S2,则S1 S2(填<、≤、=、>或≥).
16.某课外活动小组的同学在研究某种植物标本(如图所示)时,测得叶片①最大宽度是8cm,最大长度是16cm;叶片②最大宽度是7cm,最大长度是14cm;叶片③最大宽度约为6.5cm,请你用所学数学知识估算叶片③的完整叶片的最大长度,结果约为 cm.
17.在比例尺为1:5000的江阴市城区地图上,某段路的长度约为25厘米,则它的实际长度约为 米.
18.如图,在△ABC中,CD是高,CE为∠ACB的平分线.若AC=15,BC=20,CD=12,则CE的长等于 .
19.如图,点P在△ABC的边AC上,要使△ABP∽△ACB,添加一个条件 .
20.如图,在△ABC中,AC>AB,点D在BC上,且BD=BA,∠ABC的平分线BE交AD于点E,点F是AC的中点,连接EF.若四边形DCFE和△BDE的面积都为3,则△ABC的面积为 .
三.解答题
21.已知==,且2x+3y﹣z=18,求x,y,z的值.
22.已知,求m的值.
23.已知,求的值.
24.已知,求的值.
25.宽与长之比为:1的矩形叫黄金矩形,黄金矩形令人赏心悦目,它给我们以协调,匀称的美感,如图,如果在一个黄金矩形里画一个正方形,那么留下的矩形还是黄金矩形吗?请证明你的结论.
26.如图所示,正方形ABCD的边长为4 cm,P是边BC上不与点B,C重合的任意一点,连接AP,过点P作PQ⊥AP交DC于点Q.设BP的长为x cm,CQ的长为y cm.
(1)求点P在边BC上运动的过程中y的最大值;
(2)当y=时,求x的值.
27.如图,在△ABC中,∠ABC=90°,AB=BC,D是AC边所在直线上的一个动点,DE⊥BD交BC边所在直线于点E.
(1)在图①中,AD=CD,直接写出的值;
(2)在图②中,AD=2CD,直接写出的值;
(3)在图③中,AD=CD,先写出的值,再说明理由.
参考答案与试题解析
一.选择题
1.解:∵=,
∴a=b,
则==.
故选:A.
2.解:由=,得==.
故选:D.
3.解:A、1:2=3:6,即1cm,2cm,3cm,6cm成比例;
B、2:3=4:6,即2cm,3cm,4cm,6cm成比例;
C、1:=:,即1cm, cm, cm, cm成比例;
D、四条线段中,任意两条的比都不相等,因而不成比例.
故选:D.
4.解:两个矩形对应边的比不一定相等,故不一定相似;
两个等边三角形相似对应边的比相等,对应角相等,一定相似;
各有一角是80°的两个等腰三角形对应角不一定相等,故不一定相似;
任意两个菱形对应角不一定相等,故不一定相似;
故选:B.
5.解:A、∵,
∴=,此选项正确,不合题意;
B、∵,
∴=﹣,此选项错误,符合题意;
C、∵,
∴=,此选项正确,不合题意;
D、∵,
∴4x=3y,此选项正确,不合题意;
故选:B.
C 7.B 8.B
9.解:∵AB=AC=1,
∴△ABC的周长为2+k;
△BCD的周长为k+k+k2=k(2+k);
△CDE的周长为k2+k2+k3=k2(2+k);
依此类推,
第n个黄金三角形的周长为kn﹣1(2+k),
∴第2020个黄金三角形的周长为k2019(2+k).
故选:D.
10.解:过D作DH⊥AF于点H,延长DH与AB相交于点G,
∵四边形ABCD为矩形,
∴AD=BC,
∵DF=BC,
∴DA=DF,
∴AH=FH,
∵AF⊥BE,
∴DG∥BE,
∴AG=BG=,
∵矩形ABCD中,AB=DC=6,AB∥DC,
∴四边形BEDG为平行四边形,
∴DE=BG=3,
∴CE=CD﹣DE=6﹣3=3.
故选:C.
二.填空题
11.解:∵=,
∴a=b,
则==﹣.
故答案为:﹣.
12.解:∵=,
∴设a=2k,b=3k,
∴==﹣,
故答案为:﹣.
13.解:∵点P是线段AB的黄金分割点,且AP>PB,AB=10cm,
∴AP=AB≈6.18(cm).
故答案为6.18.
14.解:∵DE∥BC
∴,
∴=,
∴DE=,
故答案为:.
15.解:根据黄金分割的概念得:AP:AB=PB:AP,即AP2=PB AB,
则S1:S2=AP2:(PB AB)=1,即S1=S2.
故答案为:=.
16.解:根据叶片①②的最大长度和宽度,可得出这种植物的叶片的最大宽度:最大长度=1:2.由此可得出完整的叶片③的最大长度应是6.5×2=13cm.
故答案为:13.
17.解:设它的实际长度为x厘米,则:
1:5000=25:x,
解得x=125000.
125000厘米=1250米.
故答案为:1250.
18.解:如图,由勾股定理知AD=9,BD=16,
所以AB=AD+BD=25.
故由勾股定理逆定理知△ACB为直角三角形,
且∠ACB=90°.
作EF⊥BC,垂足为F.设EF=x,
由,
得CF=x,于是BF=20﹣x.由于EF∥AC,
所以,
即,
解得.
所以.
故答案为:.
19.解:在△ABP和△ACB中,
∵∠A=∠A,
∴当∠ABP=∠C或∠APB=∠ABC或=即AB2=AP AC时,
△ABP∽△ACB,
故答案为∠ABP=∠C或∠APB=∠ABC或AB2=AP AC.
20.解:∵BD=AB,BE是∠ABC的平分线,
∴AE=DE,
∴△BDE的面积与△ABE的面积均为3,
又∵点F是AC的中点,
∴EF是△ACD的中位线,
∴2EF=CD,EF∥DC,
∴△AEF∽△ADC,
∴S△ACD=4S△AEF,
∵四边形CDEF的面积为3,
∴△ACD的面积为4,
∴△ABC的面积为3+3+4=10.
故答案为:10.
三.解答题
21.解:由==,得
y=,z=2x.
将y=,z=2x代入2x+3y﹣z=1中,得
2x+﹣2x=18.
解得x=4,y==6,z=2x=8.
22.解:由可知:
x+y=mz,y+z=mx,z+x=my.
这几式相加可得:2(x+y+z)=m(x+y+z),
当x+y+z≠0时,有m=2,
当x+y+z=0时,有x+y=﹣z,y+z=﹣x,x+z=﹣y,m=﹣1.
故m=2或﹣1.
23.解:设=k,
则x=3k,y=4k,z=6k,
∴=.
24.解:解法1:(1)若a+b+c≠0,由等比定理有
若
=
=1,
所以a+b﹣c=c,a﹣b+c=b,﹣a+b+c=a,
于是有==8.
(2)若a+b+c=0,则a+b=﹣c,b+c=﹣a,c+a=﹣b,
于是有==﹣1.
解法2:若=k,
则a+b=(k+1)c,①
a+c=(k+1)b,②
b+c=(k+1)a.③
①+②+③有2(a+b+c)=(k+1)(a+b+c),
所以(a+b+c)(k﹣1)=0,
故有k=1或a+b+c=0.
当k=1时,==8.
当a+b+c=0时,==﹣1.
25.解:留下的矩形CDFE是黄金矩形.
证明:∵四边形ABEF是正方形,
∴AB=DC=AF,
又∵,
∴,
即点F是线段AD的黄金分割点,
∴,
即,
∴矩形CDFE是黄金矩形.
26.解:(1)∵PQ⊥AP,∴∠CPQ+∠APB=90°.
又∵∠BAP+∠APB=90°,
∴∠CPQ=∠BAP. 2分
又∵∠B=∠C=90°,
∴△ABP∽△PCQ, 4分
∴=.
∵AB=BC=4 cm,BP=x cm,CQ=y cm,
∴PC=(4-x)cm,
∴=,∴y=-x2+x,
即y=-(x-2)2+1(0∴当x=2时,y有最大值,最大值为1,即点P在边BC上运动的过程中,y的最大值为1. 6分
(2)x=2+或x=2-. 12分
27.解:(1)如图①,过点D作DF⊥BC于点F.
∵在△ABC中,∠ABC=90°,AB=BC,
∴∠ACB=45°,∴△DFC是等腰直角三角形,∴DF=CF.
∵∠DFC=∠ABC=90°,∠DCF=∠ACB=45°,
∴△DFC∽△ABC,∴=.
∵AD=CD,∴=.
设DF=CF=2k,则AB=BC=3k,∴BF=k.
易证△BDF∽△DEF,
∴===. 4分
(2)如图②,过点D作DF⊥BE于点F,同(1)可得△CDF是等腰直角三角形,∴CF=DF.
∵AD=2CD,∴AC=CD.
在△ABC与△DFC中,
∴△ABC≌△DFC,∴AB=DF,BC=FC,
∴AB=BC=FC=DF,∴BF=2DF.
易证△BDF∽△DEF,
∴==2. 8分
(3)=.
理由:如图③,过点D作DF⊥CE于点F.
∵在△ABC中,∠ABC=90°,AB=BC,
∴∠ACB=45°,
∴△DFC是等腰直角三角形,
∴DF=CF.
∵∠DFC=∠ABC=90°,∠DCF=∠ACB=45°,
∴△DFC∽△ABC,∴=.
∵AD=CD,∴==2.
设AB=m,则DF=2m,BC=m,CF=2m,
∴BF=m.
易证△BDF∽△DEF,
∴===. 14分
一.选择题
1.若=,则等于( )
A. B. C. D.
2.根据有关测定,当外界气温处于人体正常体温的黄金比值时,人体感到最舒适(人体正常体温约为37℃),这个气温大约为( )
A.23℃ B.28℃ C.30℃ D.37℃
3.如图,点G、F分别是△BCD的边BC、CD上的点,BD的延长线与GF的延长线相交于点A,DE∥BC交GA于点E,则下列结论错误的是( )
A.= B.= C.= D.=
4.下列说法正确的是( )
A.所有的菱形都相似 B.所有的矩形都相似
C.所有的正方形都相似 D.所有的梯形都相似
5.已知,那么下列等式中,不成立的是( )
A. B.
C.(y≠﹣4a) D.4x=3y
6.如图,在△ABC中,D,E两点分别在BC,AC上,且AD平分∠BAC,若∠ABE=∠C,BE与AD相交于点F,则图中与△ABD相似的是( )
A.△ABC B.△ABF C.△BFD D.△AEF
7.如图,在△ABC中,D为AB上一点,若AC2=AD AB,则( )
A.△ADC∽△CBD B.△BDC∽△BCA C.△ADC∽△ACB D.无法判断
8.如图,在△ABC中,AD是中线,BC=8,∠B=∠DAC,则线段AC的长为( )
A.4 B.4 C.6 D.4
9.如图,在△ABC中,D,E分别是AB,BC上的点,且DE∥AC.若S△BDE∶S△CDE=1∶4,则S△BDE∶S△ADC等于( )
A.1∶16 B.1∶18 C.1∶20 D.1∶24
10.在△ABC中,AB=24,AC=18,D是AC上一点,AD=12,在AB上取一点E,使以A,D,E三点为顶点的三角形与△ABC相似,则AE的长为( )
A.16 B.14
C.16或14 D.16或9
二.填空题
11.若=,则= .
12.已知:,则= .
13.已知线段AB=10cm,点P是线段AB的黄金分割点,且AP>PB,则AP≈ cm.
14.如图,D,E分别是△ABC边AB,AC上的点,DE∥BC,AD=5,BD=3,BC=4,则DE长为 .
15.已知线段AB,点P是线段AB的黄金分割点,AP>BP,设以AP为边的正方形的面积为S1,以PB、AB为边的矩形的面积为S2,则S1 S2(填<、≤、=、>或≥).
16.某课外活动小组的同学在研究某种植物标本(如图所示)时,测得叶片①最大宽度是8cm,最大长度是16cm;叶片②最大宽度是7cm,最大长度是14cm;叶片③最大宽度约为6.5cm,请你用所学数学知识估算叶片③的完整叶片的最大长度,结果约为 cm.
17.在比例尺为1:5000的江阴市城区地图上,某段路的长度约为25厘米,则它的实际长度约为 米.
18.如图,在△ABC中,CD是高,CE为∠ACB的平分线.若AC=15,BC=20,CD=12,则CE的长等于 .
19.如图,点P在△ABC的边AC上,要使△ABP∽△ACB,添加一个条件 .
20.如图,在△ABC中,AC>AB,点D在BC上,且BD=BA,∠ABC的平分线BE交AD于点E,点F是AC的中点,连接EF.若四边形DCFE和△BDE的面积都为3,则△ABC的面积为 .
三.解答题
21.已知==,且2x+3y﹣z=18,求x,y,z的值.
22.已知,求m的值.
23.已知,求的值.
24.已知,求的值.
25.宽与长之比为:1的矩形叫黄金矩形,黄金矩形令人赏心悦目,它给我们以协调,匀称的美感,如图,如果在一个黄金矩形里画一个正方形,那么留下的矩形还是黄金矩形吗?请证明你的结论.
26.如图所示,正方形ABCD的边长为4 cm,P是边BC上不与点B,C重合的任意一点,连接AP,过点P作PQ⊥AP交DC于点Q.设BP的长为x cm,CQ的长为y cm.
(1)求点P在边BC上运动的过程中y的最大值;
(2)当y=时,求x的值.
27.如图,在△ABC中,∠ABC=90°,AB=BC,D是AC边所在直线上的一个动点,DE⊥BD交BC边所在直线于点E.
(1)在图①中,AD=CD,直接写出的值;
(2)在图②中,AD=2CD,直接写出的值;
(3)在图③中,AD=CD,先写出的值,再说明理由.
参考答案与试题解析
一.选择题
1.解:∵=,
∴a=b,
则==.
故选:A.
2.解:由=,得==.
故选:D.
3.解:A、1:2=3:6,即1cm,2cm,3cm,6cm成比例;
B、2:3=4:6,即2cm,3cm,4cm,6cm成比例;
C、1:=:,即1cm, cm, cm, cm成比例;
D、四条线段中,任意两条的比都不相等,因而不成比例.
故选:D.
4.解:两个矩形对应边的比不一定相等,故不一定相似;
两个等边三角形相似对应边的比相等,对应角相等,一定相似;
各有一角是80°的两个等腰三角形对应角不一定相等,故不一定相似;
任意两个菱形对应角不一定相等,故不一定相似;
故选:B.
5.解:A、∵,
∴=,此选项正确,不合题意;
B、∵,
∴=﹣,此选项错误,符合题意;
C、∵,
∴=,此选项正确,不合题意;
D、∵,
∴4x=3y,此选项正确,不合题意;
故选:B.
C 7.B 8.B
9.解:∵AB=AC=1,
∴△ABC的周长为2+k;
△BCD的周长为k+k+k2=k(2+k);
△CDE的周长为k2+k2+k3=k2(2+k);
依此类推,
第n个黄金三角形的周长为kn﹣1(2+k),
∴第2020个黄金三角形的周长为k2019(2+k).
故选:D.
10.解:过D作DH⊥AF于点H,延长DH与AB相交于点G,
∵四边形ABCD为矩形,
∴AD=BC,
∵DF=BC,
∴DA=DF,
∴AH=FH,
∵AF⊥BE,
∴DG∥BE,
∴AG=BG=,
∵矩形ABCD中,AB=DC=6,AB∥DC,
∴四边形BEDG为平行四边形,
∴DE=BG=3,
∴CE=CD﹣DE=6﹣3=3.
故选:C.
二.填空题
11.解:∵=,
∴a=b,
则==﹣.
故答案为:﹣.
12.解:∵=,
∴设a=2k,b=3k,
∴==﹣,
故答案为:﹣.
13.解:∵点P是线段AB的黄金分割点,且AP>PB,AB=10cm,
∴AP=AB≈6.18(cm).
故答案为6.18.
14.解:∵DE∥BC
∴,
∴=,
∴DE=,
故答案为:.
15.解:根据黄金分割的概念得:AP:AB=PB:AP,即AP2=PB AB,
则S1:S2=AP2:(PB AB)=1,即S1=S2.
故答案为:=.
16.解:根据叶片①②的最大长度和宽度,可得出这种植物的叶片的最大宽度:最大长度=1:2.由此可得出完整的叶片③的最大长度应是6.5×2=13cm.
故答案为:13.
17.解:设它的实际长度为x厘米,则:
1:5000=25:x,
解得x=125000.
125000厘米=1250米.
故答案为:1250.
18.解:如图,由勾股定理知AD=9,BD=16,
所以AB=AD+BD=25.
故由勾股定理逆定理知△ACB为直角三角形,
且∠ACB=90°.
作EF⊥BC,垂足为F.设EF=x,
由,
得CF=x,于是BF=20﹣x.由于EF∥AC,
所以,
即,
解得.
所以.
故答案为:.
19.解:在△ABP和△ACB中,
∵∠A=∠A,
∴当∠ABP=∠C或∠APB=∠ABC或=即AB2=AP AC时,
△ABP∽△ACB,
故答案为∠ABP=∠C或∠APB=∠ABC或AB2=AP AC.
20.解:∵BD=AB,BE是∠ABC的平分线,
∴AE=DE,
∴△BDE的面积与△ABE的面积均为3,
又∵点F是AC的中点,
∴EF是△ACD的中位线,
∴2EF=CD,EF∥DC,
∴△AEF∽△ADC,
∴S△ACD=4S△AEF,
∵四边形CDEF的面积为3,
∴△ACD的面积为4,
∴△ABC的面积为3+3+4=10.
故答案为:10.
三.解答题
21.解:由==,得
y=,z=2x.
将y=,z=2x代入2x+3y﹣z=1中,得
2x+﹣2x=18.
解得x=4,y==6,z=2x=8.
22.解:由可知:
x+y=mz,y+z=mx,z+x=my.
这几式相加可得:2(x+y+z)=m(x+y+z),
当x+y+z≠0时,有m=2,
当x+y+z=0时,有x+y=﹣z,y+z=﹣x,x+z=﹣y,m=﹣1.
故m=2或﹣1.
23.解:设=k,
则x=3k,y=4k,z=6k,
∴=.
24.解:解法1:(1)若a+b+c≠0,由等比定理有
若
=
=1,
所以a+b﹣c=c,a﹣b+c=b,﹣a+b+c=a,
于是有==8.
(2)若a+b+c=0,则a+b=﹣c,b+c=﹣a,c+a=﹣b,
于是有==﹣1.
解法2:若=k,
则a+b=(k+1)c,①
a+c=(k+1)b,②
b+c=(k+1)a.③
①+②+③有2(a+b+c)=(k+1)(a+b+c),
所以(a+b+c)(k﹣1)=0,
故有k=1或a+b+c=0.
当k=1时,==8.
当a+b+c=0时,==﹣1.
25.解:留下的矩形CDFE是黄金矩形.
证明:∵四边形ABEF是正方形,
∴AB=DC=AF,
又∵,
∴,
即点F是线段AD的黄金分割点,
∴,
即,
∴矩形CDFE是黄金矩形.
26.解:(1)∵PQ⊥AP,∴∠CPQ+∠APB=90°.
又∵∠BAP+∠APB=90°,
∴∠CPQ=∠BAP. 2分
又∵∠B=∠C=90°,
∴△ABP∽△PCQ, 4分
∴=.
∵AB=BC=4 cm,BP=x cm,CQ=y cm,
∴PC=(4-x)cm,
∴=,∴y=-x2+x,
即y=-(x-2)2+1(0
(2)x=2+或x=2-. 12分
27.解:(1)如图①,过点D作DF⊥BC于点F.
∵在△ABC中,∠ABC=90°,AB=BC,
∴∠ACB=45°,∴△DFC是等腰直角三角形,∴DF=CF.
∵∠DFC=∠ABC=90°,∠DCF=∠ACB=45°,
∴△DFC∽△ABC,∴=.
∵AD=CD,∴=.
设DF=CF=2k,则AB=BC=3k,∴BF=k.
易证△BDF∽△DEF,
∴===. 4分
(2)如图②,过点D作DF⊥BE于点F,同(1)可得△CDF是等腰直角三角形,∴CF=DF.
∵AD=2CD,∴AC=CD.
在△ABC与△DFC中,
∴△ABC≌△DFC,∴AB=DF,BC=FC,
∴AB=BC=FC=DF,∴BF=2DF.
易证△BDF∽△DEF,
∴==2. 8分
(3)=.
理由:如图③,过点D作DF⊥CE于点F.
∵在△ABC中,∠ABC=90°,AB=BC,
∴∠ACB=45°,
∴△DFC是等腰直角三角形,
∴DF=CF.
∵∠DFC=∠ABC=90°,∠DCF=∠ACB=45°,
∴△DFC∽△ABC,∴=.
∵AD=CD,∴==2.
设AB=m,则DF=2m,BC=m,CF=2m,
∴BF=m.
易证△BDF∽△DEF,
∴===. 14分
