2021-2022学年北师大版九年级数学上册第3章概率的进一步认识期末综合复习训练(Word版含解析)
文档属性
| 名称 | 2021-2022学年北师大版九年级数学上册第3章概率的进一步认识期末综合复习训练(Word版含解析) |  | |
| 格式 | doc | ||
| 文件大小 | 239.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-12-28 08:39:20 | ||
图片预览



文档简介
2021-2022学年北师大版九年级数学上册《第3章概率的进一步认识》
期末综合复习训练2(附答案)
1.在相同条件下,移植10000棵幼苗,有8000棵幼苗成活,估计在相同条件下移植一棵这种幼苗成活的概率为( )
A.0.1 B.0.2 C.0.9 D.0.8
2.在一个不透明的口袋里有1个红球、1个黄球、1个蓝球,这三种颜色的小球除颜色外都相同.摇匀后,一次随机摸出2个球,则摸出的两个小球中有一个为红球的概率为( )
A. B. C. D.
3.从1,2,3中任取一个数作为十位上的数字,从4,5中任取一个数作为个位上的数字,组成的两位数是偶数的概率为( )
A. B. C. D.
4.下列说法正确的是( )
A.掷一枚质地均匀的骰子,掷得的点数为3的概率是
B.某种彩票中奖的概率是,那么买10000张这种彩票一定会中奖
C.掷两枚质地均匀的硬币,“两枚硬币都是正面朝上”的概率与“一枚硬币正面朝上,一枚硬币反面朝上”的概率相同
D.通过大量重复试验,可以用频率估计概率
5.甲、乙两名同学在一次用频率去估计概率的实验中,统计某一结果出现的频率绘出的统计图如图所示,则符合这一结果的实验可能是( )
A.抛一枚硬币,连续两次出现正面的概率
B.在“石头、剪刀、布”的游戏中,小明随机出的是“剪刀”
C.任意写一个正整数,它能被5整除的概率
D.掷一枚正六面体的骰子,出现1点的概率
6.小明、小颖和小丽三位同学随机地站成一排做游戏,小明站在排头的概率是( )
A.1 B. C. D.
7.学校60周年校庆,要从甲、乙、丙三人中选两名志愿者,甲被选中的概率是( )
A. B. C. D.1
8.从1,﹣2,﹣3三个数中,随机抽取两个数相乘,积是正数的概率是( )
A.0 B. C. D.1
9.淘淘和丽丽是九年级学生,在5月份进行的物理、化学、生物实验技能考试中,考试科目要求三选一,并且采取抽签方式取得,那么他们两人都抽到物理实验的概率是( )
A. B. C. D.
10.某学习小组进行“用频率估计概率”的试验时,统计了某一结果出现的频率如下表,则符合这一结果的试验可能是( )
试验次数 100 200 500 800 1000 1200
实验频率 0.343 0.326 0.335 0.330 0.331 0.330
A.先后两次抛掷一枚质地均匀的硬币,两次都是反面朝上
B.先后两次掷一枚质地均匀的骰子,两次的点数和不大于6
C.将一个篮球和一个足球随机放入三个不同的篮子中,恰有一个篮子为空
D.从两男两女四人中抽取两人参加朗读比赛,两人性别相同
11.学校组织户外研学活动,安排给九年级三辆车,小刚与小兰都可以从三辆车中任选一辆搭乘,则小刚和小兰搭乘同一辆车的概率为 .
12.在学校举办的“美德少年”评选活动中,九年级一班有甲,乙,丙,丁共4名学生获奖.班主任决定在这4名获奖学生中随机选出2名学生在班级进行主题演讲,则甲被选中的概率为 .
13.在一个不透明的袋子里装有红球6个,黄球若干个,这些球除颜色外都相同,小明通过多次试验发现,摸出红球的频率稳定在0.3左右,则袋子中黄球的个数可能是 个.
14.有五张正面分别标有数字﹣8,,0,2,8的卡片,它们除数字不同外其余全部相同.现将五张卡片背面朝上,洗匀后从中随机抽取两张,则抽取的两张卡片上的数字之积为一个非负数的概率是 .
15.一枚硬币抛三次都是正面向上的概率是 .
16.某校打算组织八年级90名团员开展一次以“爱国教育”为主题的观影活动.目前有A:《长津湖》、B:《我和我的父辈》、C:《雪纷飞》三部电影可供选择,小华和小军参加了此次观影活动.
(1)小军选择看《长津湖》的概率为 .
(2)请用画树状图或列表的方法,求出小华和小军选择看同一部电影的概率.
17.一只不透明的袋子中装有1个白球、2个黄球和1个红球,每个球除颜色外都相同,将球摇匀.
(1)求从中任意摸出1个白球的概率.
(2)从中任意摸出2个球,请利用画树状图或列表法,求出摸到2个都是黄球的概率.
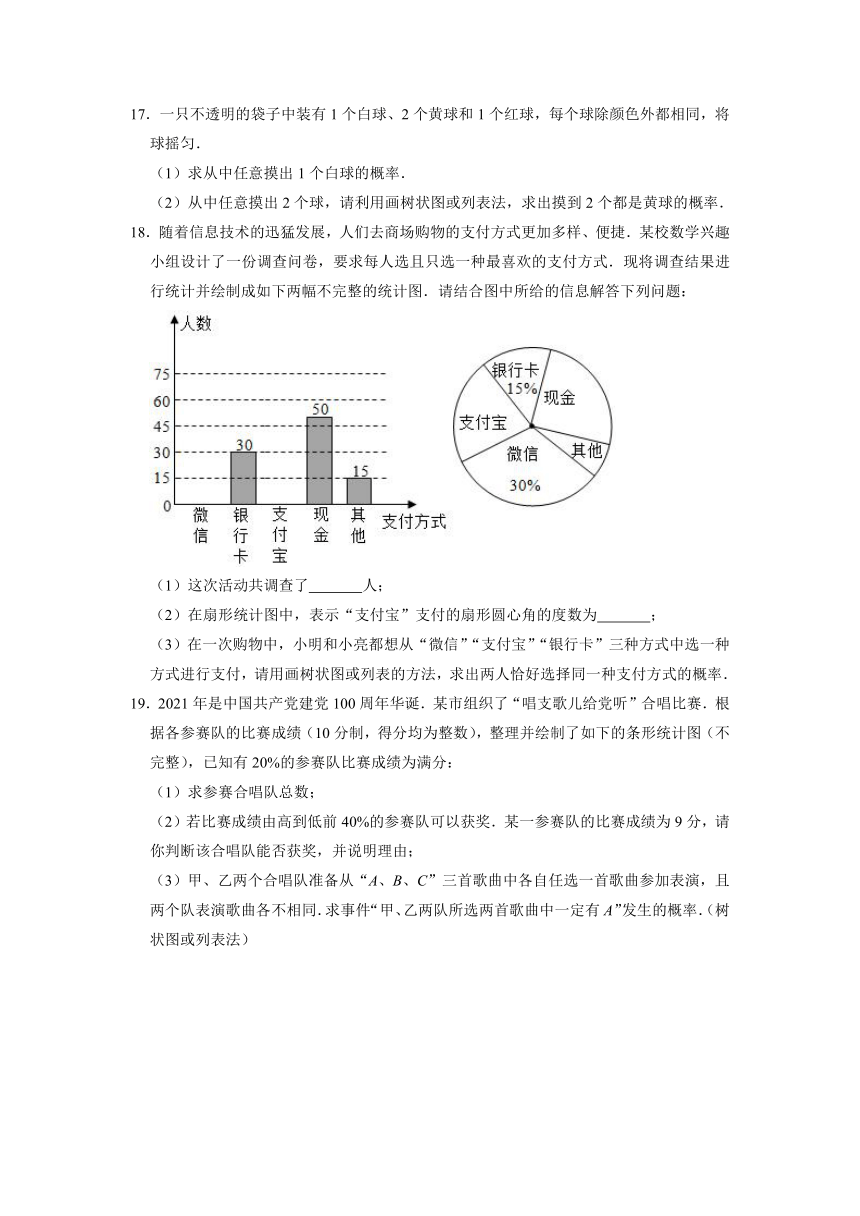
18.随着信息技术的迅猛发展,人们去商场购物的支付方式更加多样、便捷.某校数学兴趣小组设计了一份调查问卷,要求每人选且只选一种最喜欢的支付方式.现将调查结果进行统计并绘制成如下两幅不完整的统计图.请结合图中所给的信息解答下列问题:
(1)这次活动共调查了 人;
(2)在扇形统计图中,表示“支付宝”支付的扇形圆心角的度数为 ;
(3)在一次购物中,小明和小亮都想从“微信”“支付宝”“银行卡”三种方式中选一种方式进行支付,请用画树状图或列表的方法,求出两人恰好选择同一种支付方式的概率.
19.2021年是中国共产党建党100周年华诞.某市组织了“唱支歌儿给党听”合唱比赛.根据各参赛队的比赛成绩(10分制,得分均为整数),整理并绘制了如下的条形统计图(不完整),已知有20%的参赛队比赛成绩为满分:
(1)求参赛合唱队总数;
(2)若比赛成绩由高到低前40%的参赛队可以获奖.某一参赛队的比赛成绩为9分,请你判断该合唱队能否获奖,并说明理由;
(3)甲、乙两个合唱队准备从“A、B、C”三首歌曲中各自任选一首歌曲参加表演,且两个队表演歌曲各不相同.求事件“甲、乙两队所选两首歌曲中一定有A”发生的概率.(树状图或列表法)
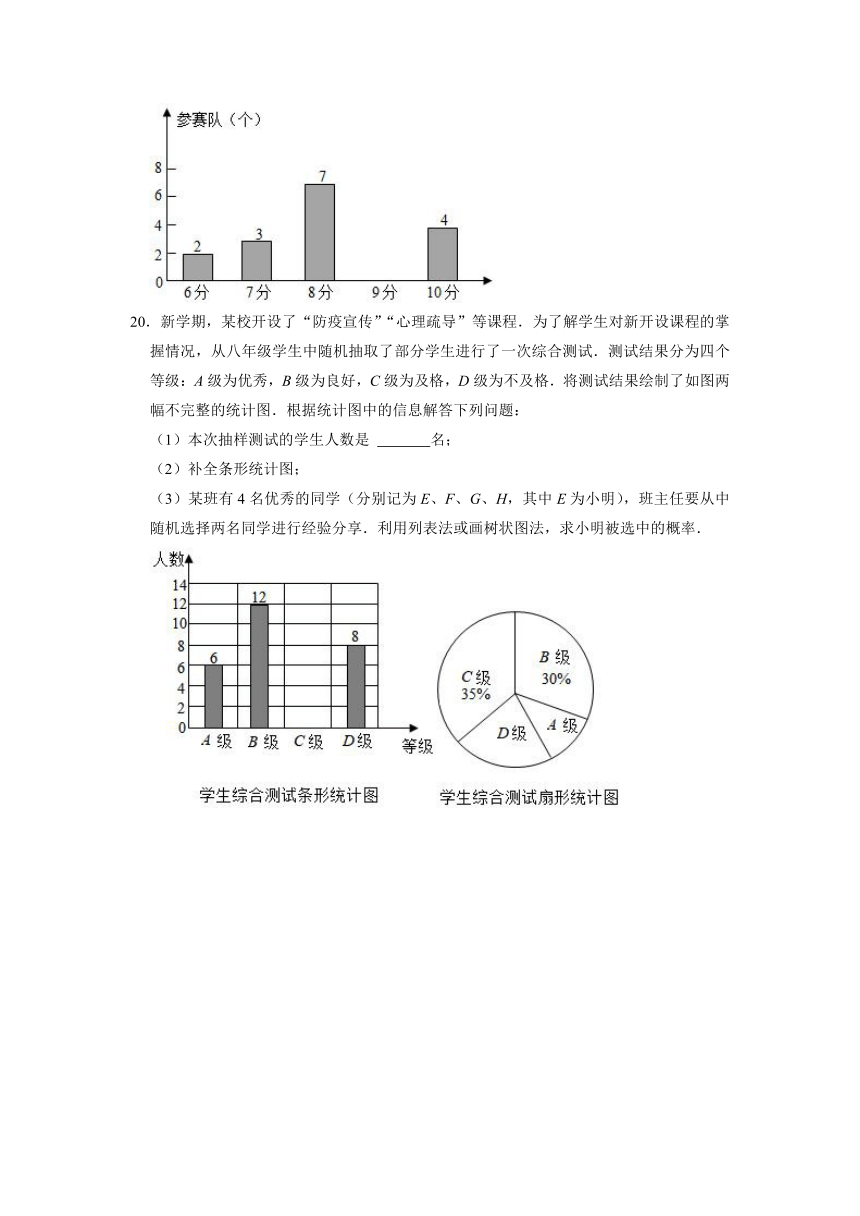
20.新学期,某校开设了“防疫宣传”“心理疏导”等课程.为了解学生对新开设课程的掌握情况,从八年级学生中随机抽取了部分学生进行了一次综合测试.测试结果分为四个等级:A级为优秀,B级为良好,C级为及格,D级为不及格.将测试结果绘制了如图两幅不完整的统计图.根据统计图中的信息解答下列问题:
(1)本次抽样测试的学生人数是 名;
(2)补全条形统计图;
(3)某班有4名优秀的同学(分别记为E、F、G、H,其中E为小明),班主任要从中随机选择两名同学进行经验分享.利用列表法或画树状图法,求小明被选中的概率.
参考答案
1.解:估计在相同条件下移植一棵这种幼苗成活的概率为=0.8,
故选:D.
2.解:画树状图如下:
共有6种等可能的结果,其中摸出的两个小球中有一个为红球的结果有4种,
则摸出的两个小球中有一个为红球的概率为=.
故选:D.
3.解:画树状图如下:
共有6种等可能的结果,组成的两位数是偶数的结果有3个,
∴组成的两位数是偶数的概率为=,
故选:A.
4.解:A.掷一枚质地均匀的骰子,掷得的点数为3的概率是,此选项错误,不符合题意;
B.某种彩票中奖的概率是,那么买10000张这种彩票不一定会中奖,原命题说法是错误的,此选项不符合题意;
C.连续掷两枚质地均匀的硬币,“两枚硬币都是正面朝上”的概率是,“一枚硬币正面朝上,一枚硬币反面朝上”的概率是,此选项错误,不符合题意;
D.通过大量重复试验,可以用频率估计概率,此选项符合题意;
故选:D.
5.解:A、掷一枚硬币,连续两次出现正面的概率为,故此选项不符合题意;
B、在“石头、剪刀、布”的游戏中,小明随机出的是“剪刀”的概率为,此选项符合题意;
C、任意写出一个正整数,能被5整除的概率为,故此选项不符合题意;
D、掷一枚正六面体的骰子,出现1点的概率为,故此选项不符合题意;
故选:B.
6.解:把小明、小颖和小丽三位同学分别记为A、B、C,
画树状图如下:
共有6种等可能的结果,小明站在排头的结果有2种,
∴小明站在排头的概率为=,
故选:D.
7.解:画树状图如下:
共有6种等可能的结果,其中甲被选中的结果有4种,
∴甲被选中的概率为=,
故选:C.
8.解:画树状图得:
∵共有6种等可能的结果,随机抽取两个数相乘,积是正数的有2种情况,
∴随机抽取两个数相乘,积是正数的概率是:=.
故选:B.
9.解:画树状图为:
因为共有9种等可能的结果数,其中他们两人都抽到物理实验的结果数为1,
所以他们两人都抽到物理实验的概率是.
故选:B.
10.解:A.先后两次抛掷一枚质地均匀的硬币,两次都是反面朝上的概率为,与表格不符,不符合题意;
B.先后两次掷一枚质地均匀的骰子,两次的点数和不大于3的概率为=,与表格不符,不符合题意;
C.将一个篮球和一个足球随机放入三个不同的篮子中,恰有一个篮子为空,概率为,与表格不符,不符合题意;
D.从两男两女四人中抽取两人参加朗读比赛,两人性别相同的概率为≈0.33,与表格相符,符合题意;
故选:D.
11.解:用A,B,C分别表示给九年级的三辆车,
画树状图得
∵共有9种等可能的结果,其中小刚和小兰搭乘同一辆车的有3种情况,
∴小刚和小兰搭乘同一辆车的概率为=.
故答案为:.
12.解:画树状图如下:
所有出现的等可能性结果共有12种,其中甲被选中的结果有6种,
所以甲被选中的的概率为=.
故答案为:.
13.解:设袋子中黄球的个数可能有x个,根据题意得:
=0.3,
解得:x=14,
经检验x=14是原方程的解,
答:袋子中黄球的个数可能是14个.
故答案为:14.
14.解:画树状图如下:
共有20种等可能的结果,抽取的两张卡片上的数字之积为一个非负数的结果有12种,
∴抽取的两张卡片上的数字之积为一个非负数的概率是=,
故答案为:.
15.解:画树状图为:
共有8种等可能的结果,其中三次都是正面向上的结果数为1,
所以三次都是正面向上的概率为.
故答案为.
16.解:(1)小军选择看《长津湖》的概率为,
故答案为:;
(2)画树状图如下:
共有9种等可能的结果,小华和小军选择看同一部电影的结果有3种,
∴小华和小军选择看同一部电影的概率为=.
17.解:(1)∵不透明的袋子中装有1个白球、2个黄球和1个红球,共4个球,
∴从中任意摸出1个白球的概率是;
(2)根据题意列表如下:
白 黄 黄 红
白 (白,黄) (白,黄) (白,红)
黄 (黄,白) (黄,黄) (黄,红)
黄 (黄,白) (黄,黄) (黄,红)
红 (红,白) (红,黄) (红,黄)
共有12中等可能的情况数,其中摸到2个都是黄球的有2种,
则摸到2个都是黄球的概率是=.
18.解:(1)这次活动共调查的人数为30÷15%=200(人),
故答案为:200;
(2)在扇形统计图中,表示“支付宝”支付的扇形圆心角的度数为360°×=81°,
故答案为:81°;
(3)将微信记为A,支付宝记为B,银行卡记为C,列表格如下:
A B C
A (A,A) (A,B) (A,C)
B (B,A) (B,B) (B,C)
C (C,A) (C,B) (C,C)
共有9种等可能性的结果,其中两人恰好选择同一种支付方式的结果有3种,
则P(两人恰好选择同一种支付方式)=.
19.解:(1)参赛合唱队总数为4÷20%=20(个);
(2)可以获奖的合唱队总数为20×40%=8(个),
∴得9分的合唱队有20﹣(2+3+7+4)=4(个),
∴参赛成绩为9分的合唱队可以获奖;
(3)列表如下:
A B C
A (B,A) (C,A)
B (A,B) (C,B)
C (A,C) (B,C)
由表知共有6种等可能结果,其中甲、乙两队所选两首歌曲中一定有A的有4种结果,
∴事件“甲、乙两队所选两首歌曲中一定有A”发生的概率为=.
20.解:(1)本次抽样测试的学生人数是:12÷30%=40(名);
(2)C级人数为:40﹣6﹣12﹣8=14(名),
补全统计图如下:
(3)画树状图得:
∵共有12种等可能的结果,选中小明的有6种情况,
∴选中小明的概率为.
期末综合复习训练2(附答案)
1.在相同条件下,移植10000棵幼苗,有8000棵幼苗成活,估计在相同条件下移植一棵这种幼苗成活的概率为( )
A.0.1 B.0.2 C.0.9 D.0.8
2.在一个不透明的口袋里有1个红球、1个黄球、1个蓝球,这三种颜色的小球除颜色外都相同.摇匀后,一次随机摸出2个球,则摸出的两个小球中有一个为红球的概率为( )
A. B. C. D.
3.从1,2,3中任取一个数作为十位上的数字,从4,5中任取一个数作为个位上的数字,组成的两位数是偶数的概率为( )
A. B. C. D.
4.下列说法正确的是( )
A.掷一枚质地均匀的骰子,掷得的点数为3的概率是
B.某种彩票中奖的概率是,那么买10000张这种彩票一定会中奖
C.掷两枚质地均匀的硬币,“两枚硬币都是正面朝上”的概率与“一枚硬币正面朝上,一枚硬币反面朝上”的概率相同
D.通过大量重复试验,可以用频率估计概率
5.甲、乙两名同学在一次用频率去估计概率的实验中,统计某一结果出现的频率绘出的统计图如图所示,则符合这一结果的实验可能是( )
A.抛一枚硬币,连续两次出现正面的概率
B.在“石头、剪刀、布”的游戏中,小明随机出的是“剪刀”
C.任意写一个正整数,它能被5整除的概率
D.掷一枚正六面体的骰子,出现1点的概率
6.小明、小颖和小丽三位同学随机地站成一排做游戏,小明站在排头的概率是( )
A.1 B. C. D.
7.学校60周年校庆,要从甲、乙、丙三人中选两名志愿者,甲被选中的概率是( )
A. B. C. D.1
8.从1,﹣2,﹣3三个数中,随机抽取两个数相乘,积是正数的概率是( )
A.0 B. C. D.1
9.淘淘和丽丽是九年级学生,在5月份进行的物理、化学、生物实验技能考试中,考试科目要求三选一,并且采取抽签方式取得,那么他们两人都抽到物理实验的概率是( )
A. B. C. D.
10.某学习小组进行“用频率估计概率”的试验时,统计了某一结果出现的频率如下表,则符合这一结果的试验可能是( )
试验次数 100 200 500 800 1000 1200
实验频率 0.343 0.326 0.335 0.330 0.331 0.330
A.先后两次抛掷一枚质地均匀的硬币,两次都是反面朝上
B.先后两次掷一枚质地均匀的骰子,两次的点数和不大于6
C.将一个篮球和一个足球随机放入三个不同的篮子中,恰有一个篮子为空
D.从两男两女四人中抽取两人参加朗读比赛,两人性别相同
11.学校组织户外研学活动,安排给九年级三辆车,小刚与小兰都可以从三辆车中任选一辆搭乘,则小刚和小兰搭乘同一辆车的概率为 .
12.在学校举办的“美德少年”评选活动中,九年级一班有甲,乙,丙,丁共4名学生获奖.班主任决定在这4名获奖学生中随机选出2名学生在班级进行主题演讲,则甲被选中的概率为 .
13.在一个不透明的袋子里装有红球6个,黄球若干个,这些球除颜色外都相同,小明通过多次试验发现,摸出红球的频率稳定在0.3左右,则袋子中黄球的个数可能是 个.
14.有五张正面分别标有数字﹣8,,0,2,8的卡片,它们除数字不同外其余全部相同.现将五张卡片背面朝上,洗匀后从中随机抽取两张,则抽取的两张卡片上的数字之积为一个非负数的概率是 .
15.一枚硬币抛三次都是正面向上的概率是 .
16.某校打算组织八年级90名团员开展一次以“爱国教育”为主题的观影活动.目前有A:《长津湖》、B:《我和我的父辈》、C:《雪纷飞》三部电影可供选择,小华和小军参加了此次观影活动.
(1)小军选择看《长津湖》的概率为 .
(2)请用画树状图或列表的方法,求出小华和小军选择看同一部电影的概率.
17.一只不透明的袋子中装有1个白球、2个黄球和1个红球,每个球除颜色外都相同,将球摇匀.
(1)求从中任意摸出1个白球的概率.
(2)从中任意摸出2个球,请利用画树状图或列表法,求出摸到2个都是黄球的概率.
18.随着信息技术的迅猛发展,人们去商场购物的支付方式更加多样、便捷.某校数学兴趣小组设计了一份调查问卷,要求每人选且只选一种最喜欢的支付方式.现将调查结果进行统计并绘制成如下两幅不完整的统计图.请结合图中所给的信息解答下列问题:
(1)这次活动共调查了 人;
(2)在扇形统计图中,表示“支付宝”支付的扇形圆心角的度数为 ;
(3)在一次购物中,小明和小亮都想从“微信”“支付宝”“银行卡”三种方式中选一种方式进行支付,请用画树状图或列表的方法,求出两人恰好选择同一种支付方式的概率.
19.2021年是中国共产党建党100周年华诞.某市组织了“唱支歌儿给党听”合唱比赛.根据各参赛队的比赛成绩(10分制,得分均为整数),整理并绘制了如下的条形统计图(不完整),已知有20%的参赛队比赛成绩为满分:
(1)求参赛合唱队总数;
(2)若比赛成绩由高到低前40%的参赛队可以获奖.某一参赛队的比赛成绩为9分,请你判断该合唱队能否获奖,并说明理由;
(3)甲、乙两个合唱队准备从“A、B、C”三首歌曲中各自任选一首歌曲参加表演,且两个队表演歌曲各不相同.求事件“甲、乙两队所选两首歌曲中一定有A”发生的概率.(树状图或列表法)
20.新学期,某校开设了“防疫宣传”“心理疏导”等课程.为了解学生对新开设课程的掌握情况,从八年级学生中随机抽取了部分学生进行了一次综合测试.测试结果分为四个等级:A级为优秀,B级为良好,C级为及格,D级为不及格.将测试结果绘制了如图两幅不完整的统计图.根据统计图中的信息解答下列问题:
(1)本次抽样测试的学生人数是 名;
(2)补全条形统计图;
(3)某班有4名优秀的同学(分别记为E、F、G、H,其中E为小明),班主任要从中随机选择两名同学进行经验分享.利用列表法或画树状图法,求小明被选中的概率.
参考答案
1.解:估计在相同条件下移植一棵这种幼苗成活的概率为=0.8,
故选:D.
2.解:画树状图如下:
共有6种等可能的结果,其中摸出的两个小球中有一个为红球的结果有4种,
则摸出的两个小球中有一个为红球的概率为=.
故选:D.
3.解:画树状图如下:
共有6种等可能的结果,组成的两位数是偶数的结果有3个,
∴组成的两位数是偶数的概率为=,
故选:A.
4.解:A.掷一枚质地均匀的骰子,掷得的点数为3的概率是,此选项错误,不符合题意;
B.某种彩票中奖的概率是,那么买10000张这种彩票不一定会中奖,原命题说法是错误的,此选项不符合题意;
C.连续掷两枚质地均匀的硬币,“两枚硬币都是正面朝上”的概率是,“一枚硬币正面朝上,一枚硬币反面朝上”的概率是,此选项错误,不符合题意;
D.通过大量重复试验,可以用频率估计概率,此选项符合题意;
故选:D.
5.解:A、掷一枚硬币,连续两次出现正面的概率为,故此选项不符合题意;
B、在“石头、剪刀、布”的游戏中,小明随机出的是“剪刀”的概率为,此选项符合题意;
C、任意写出一个正整数,能被5整除的概率为,故此选项不符合题意;
D、掷一枚正六面体的骰子,出现1点的概率为,故此选项不符合题意;
故选:B.
6.解:把小明、小颖和小丽三位同学分别记为A、B、C,
画树状图如下:
共有6种等可能的结果,小明站在排头的结果有2种,
∴小明站在排头的概率为=,
故选:D.
7.解:画树状图如下:
共有6种等可能的结果,其中甲被选中的结果有4种,
∴甲被选中的概率为=,
故选:C.
8.解:画树状图得:
∵共有6种等可能的结果,随机抽取两个数相乘,积是正数的有2种情况,
∴随机抽取两个数相乘,积是正数的概率是:=.
故选:B.
9.解:画树状图为:
因为共有9种等可能的结果数,其中他们两人都抽到物理实验的结果数为1,
所以他们两人都抽到物理实验的概率是.
故选:B.
10.解:A.先后两次抛掷一枚质地均匀的硬币,两次都是反面朝上的概率为,与表格不符,不符合题意;
B.先后两次掷一枚质地均匀的骰子,两次的点数和不大于3的概率为=,与表格不符,不符合题意;
C.将一个篮球和一个足球随机放入三个不同的篮子中,恰有一个篮子为空,概率为,与表格不符,不符合题意;
D.从两男两女四人中抽取两人参加朗读比赛,两人性别相同的概率为≈0.33,与表格相符,符合题意;
故选:D.
11.解:用A,B,C分别表示给九年级的三辆车,
画树状图得
∵共有9种等可能的结果,其中小刚和小兰搭乘同一辆车的有3种情况,
∴小刚和小兰搭乘同一辆车的概率为=.
故答案为:.
12.解:画树状图如下:
所有出现的等可能性结果共有12种,其中甲被选中的结果有6种,
所以甲被选中的的概率为=.
故答案为:.
13.解:设袋子中黄球的个数可能有x个,根据题意得:
=0.3,
解得:x=14,
经检验x=14是原方程的解,
答:袋子中黄球的个数可能是14个.
故答案为:14.
14.解:画树状图如下:
共有20种等可能的结果,抽取的两张卡片上的数字之积为一个非负数的结果有12种,
∴抽取的两张卡片上的数字之积为一个非负数的概率是=,
故答案为:.
15.解:画树状图为:
共有8种等可能的结果,其中三次都是正面向上的结果数为1,
所以三次都是正面向上的概率为.
故答案为.
16.解:(1)小军选择看《长津湖》的概率为,
故答案为:;
(2)画树状图如下:
共有9种等可能的结果,小华和小军选择看同一部电影的结果有3种,
∴小华和小军选择看同一部电影的概率为=.
17.解:(1)∵不透明的袋子中装有1个白球、2个黄球和1个红球,共4个球,
∴从中任意摸出1个白球的概率是;
(2)根据题意列表如下:
白 黄 黄 红
白 (白,黄) (白,黄) (白,红)
黄 (黄,白) (黄,黄) (黄,红)
黄 (黄,白) (黄,黄) (黄,红)
红 (红,白) (红,黄) (红,黄)
共有12中等可能的情况数,其中摸到2个都是黄球的有2种,
则摸到2个都是黄球的概率是=.
18.解:(1)这次活动共调查的人数为30÷15%=200(人),
故答案为:200;
(2)在扇形统计图中,表示“支付宝”支付的扇形圆心角的度数为360°×=81°,
故答案为:81°;
(3)将微信记为A,支付宝记为B,银行卡记为C,列表格如下:
A B C
A (A,A) (A,B) (A,C)
B (B,A) (B,B) (B,C)
C (C,A) (C,B) (C,C)
共有9种等可能性的结果,其中两人恰好选择同一种支付方式的结果有3种,
则P(两人恰好选择同一种支付方式)=.
19.解:(1)参赛合唱队总数为4÷20%=20(个);
(2)可以获奖的合唱队总数为20×40%=8(个),
∴得9分的合唱队有20﹣(2+3+7+4)=4(个),
∴参赛成绩为9分的合唱队可以获奖;
(3)列表如下:
A B C
A (B,A) (C,A)
B (A,B) (C,B)
C (A,C) (B,C)
由表知共有6种等可能结果,其中甲、乙两队所选两首歌曲中一定有A的有4种结果,
∴事件“甲、乙两队所选两首歌曲中一定有A”发生的概率为=.
20.解:(1)本次抽样测试的学生人数是:12÷30%=40(名);
(2)C级人数为:40﹣6﹣12﹣8=14(名),
补全统计图如下:
(3)画树状图得:
∵共有12种等可能的结果,选中小明的有6种情况,
∴选中小明的概率为.
同课章节目录
- 第一章 特殊平行四边形
- 1 菱形的性质与判定
- 2 矩形的性质与判定
- 3 正方形的性质与判定
- 第二章 一元二次方程
- 1 认识一元二次方程
- 2 用配方法求解一元二次方程
- 3 用公式法求解一元二次方程
- 4 用因式分解法求解一元二次方程
- 5 一元二次方程的根与系数的关系
- 6 应用一元二次方程
- 第三章 概率的进一步认识
- 1 用树状图或表格求概率
- 2 用频率估计概率
- 第四章 图形的相似
- 1 成比例线段
- 2 平行线分线段成比例
- 3 相似多边形
- 4 探索三角形相似的条件
- 5 相似三角形判定定理的证明
- 6 利用相似三角形测高
- 7 相似三角形的性质
- 8 图形的位似
- 第五章 投影与视图
- 1 投影
- 2 视图
- 第六章 反比例函数
- 1 反比例函数
- 2 反比例函数的图象与性质
- 3 反比例函数的应用
