七年级下册数学期中考试试卷(附答案)
图片预览


文档简介
七年级数学检测试题
时间:90分钟 总分:120分
一、选择题(每小题3分,共计36分)请把正确答案的序号填入表中
1.下列图形中,可用么∠1,∠AOB,∠O三种方法表示同一个角的是( )
2.如图,如果∠AOC=∠BOD,则∠AOB与∠DOC的大小关系是( )
A.∠AOB>∠DOC B.∠AOB<∠DOC C.∠AOB=∠DOC D.无法比较
3.一个游戏的中将率是1%,小花买100张奖券,下列说法正确的是()
A.一定会中奖 B.一定不中奖 C.中奖的可能性大 D.中奖的可能性小
4.从一只船上看一小岛,方向为北偏东35°,从小岛上看这只船,其方向为( )
A.南偏西35° B.南偏东55° C.北偏东55° D.北偏西35°
5.如图,下列说法中正确的是( )
A.∠1与∠C是同位角 B.∠1与∠3是同旁内角
C.∠3与∠C是内错角 D.∠1与∠3是对顶角
6.如图,根据下列条件,不能判定AB∥DF的是( )
A.∠A+∠2=180° B.∠A=∠3 C.∠1=∠4 D.∠1=∠A
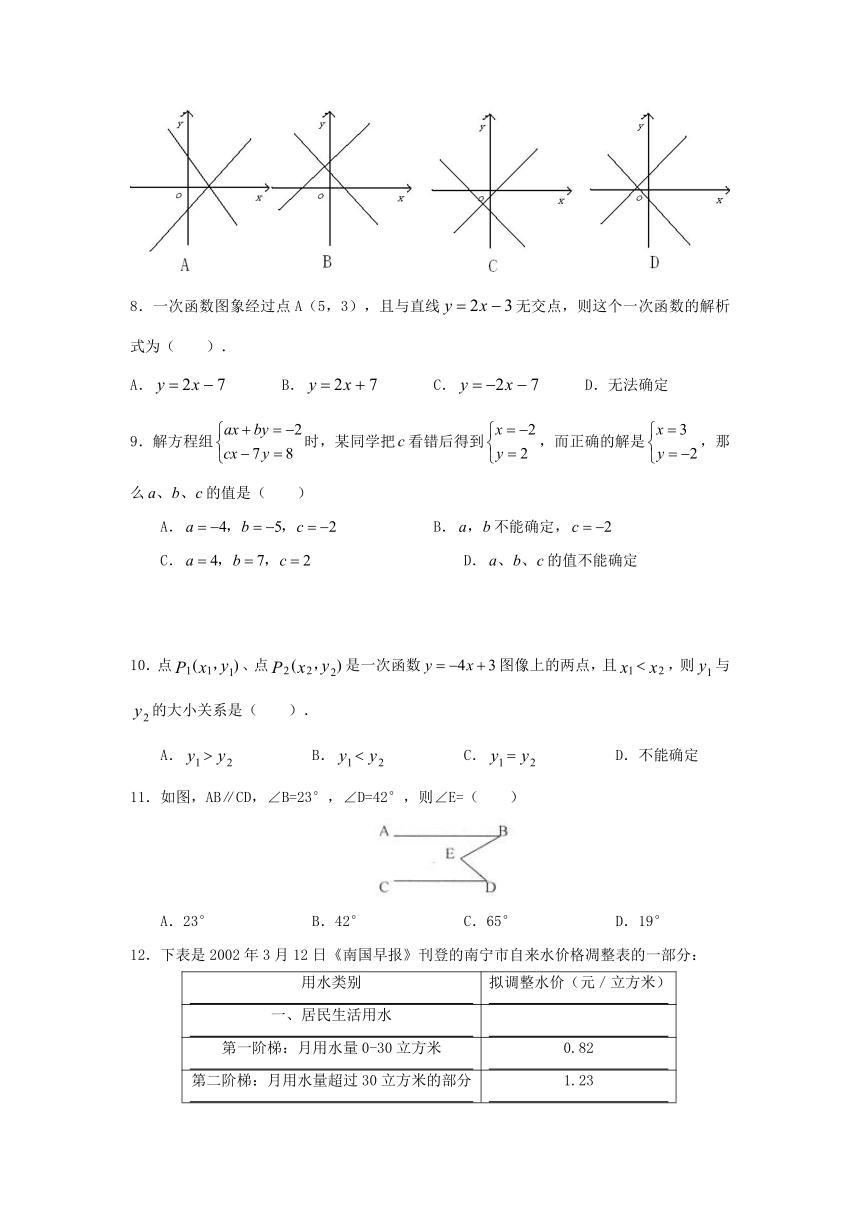
7.一次函数y1=ax+b与y2=bx+a在同一直角坐标系
内的函数图像可能是
8.一次函数图象经过点A(5,3),且与直线无交点,则这个一次函数的解析式为( ).
A. B. C. D.无法确定
9.解方程组时,某同学把看错后得到,而正确的解是,那么的值是( )
A. B.不能确定,
C. D.的值不能确定
10.点、点是一次函数图像上的两点,且,则与的大小关系是( ).
A. B. C. D.不能确定
11.如图,AB∥CD,∠B=23°,∠D=42°,则∠E=( )
A.23° B.42° C.65° D.19°
12.下表是2002年3月12日《南国早报》刊登的南宁市自来水价格凋整表的一部分:
用水类别
拟调整水价(元/立方米)
一、居民生活用水
第一阶梯:月用水量0-30立方米
0.82
第二阶梯:月用水量超过30立方米的部分
1.23
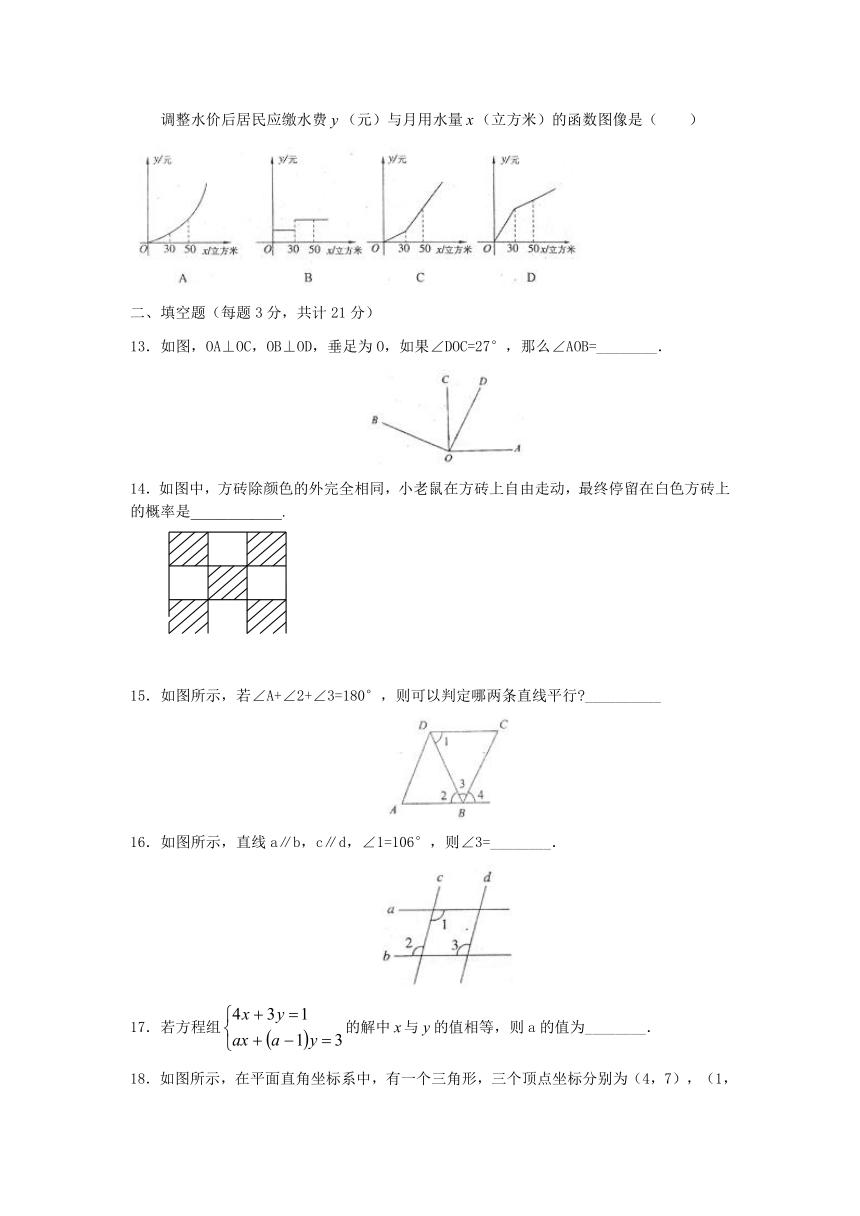
调整水价后居民应缴水费(元)与月用水量(立方米)的函数图像是( )
二、填空题(每题3分,共计21分)
13.如图,OA⊥OC,OB⊥OD,垂足为O,如果∠DOC=27°,那么∠AOB=________.
14.如图中,方砖除颜色的外完全相同,小老鼠在方砖上自由走动,最终停留在白色方砖上的概率是____________.
15.如图所示,若∠A+∠2+∠3=180°,则可以判定哪两条直线平行?__________
16.如图所示,直线a∥b,c∥d,∠1=106°,则∠3=________.
17.若方程组的解中与的值相等,则a的值为________.
18.如图所示,在平面直角坐标系中,有一个三角形,三个顶点坐标分别为(4,7),(1,1),(8,3).则这个三角形的面积是________.
19.已知方程组的解是,则的解是_______.
三、解答题(共63分)
20、(1)(8分)解方程组
(2)(8分)已知方程组的解能使等式成立,求的值.
21.(本题满分8分)已知在平面直角坐标系中,点A,点B的坐标分别为A(0,0),B(0,4)点C在x轴上,且ABC的面积为6,求点C的坐标。
22.(本题满分8分)如下图所示,已知点B、E分别在AC、DF上,BD、CE均与AF相交,∠1=∠2,∠C=∠D,
求证:∠A=∠F
23.(本题满分10分)
已知金属棒的长度是温度t的一次函数,现有一根金属棒,在0℃时长度是200厘米,温度每升高1℃,它就伸长0.002厘米。
(1)求这根金属棒的长度与温度t的函数关系式;
(2)当温度为100℃时,这根金属棒的长度是多少?
(3)当这根金属棒加热后长度伸长到201.6厘米时,这根金属棒的温度是多少?
24.(10分)某地生产一种绿色蔬菜,若在市场上直接销售,每吨利润为1000元,经粗加工后销售,每吨利润可达4500元,经精加工后销售,每吨利润涨至7500元,当地一家公司收购这种蔬菜140吨,该公司加工厂的生产能力是:如果对蔬菜进行粗加工,每天可加工16吨,若果进行精加工,每天可加工6吨,但两种加工方式不能同时进行,受季节的条件限制,公司必须在15天内将这些蔬菜全部销售或加工完毕,为此公司研制了三种方案:
方案一:将蔬菜全部进行粗加工;
方案二:尽可能多的对蔬菜进行精加工,没有来得及进行加工的蔬菜,在市场上销售;
方案三:将部分蔬菜进行粗加工,其余蔬菜进行精加工,并恰好在15天内完成。
你认为选择哪种方案获利最多?为什么?
25.(本题满分11分)
“五一黄金周”的某一天,小明全家上午8时自驾小汽车从家里出发,到距离180千米的某著名旅游景点游玩.该小汽车离家的距离s(千米)与时间t(时)的关系可以用图中的曲线表示.根据图象提供的有关信息,解答下列问题:
(1)小明全家在旅游景点游玩了多少小时?
(2)求出返程途中,s(千米)与时间t(时)的函数关系,并回答小明全家到家是什么时间?
(3)若出发时汽车油箱中存油15升,该汽车的油箱总容量为35升,汽车每行驶1千米耗油升.请你就“何时加油和加油量”给小明全家提出一个合理化的建议.(加油所用时间忽略不计)
参考答案
一、选择题(每小题3分,共计36分)
1-5 BCDAC 6-10 DAAAA 11-12 CC
二、填空题(每题3分,共计21分)
13.153° 14. 15.AD∥BC
16.106° 17.a=11 18.18
19.
三、解答题(共63分)
20.(1)(说明:只有结果没有过程,不得分)
(2)解:由题意得方程组
解得
把带入方程
得
21.设点C坐标是(x,0)根据题意得,AB×AC=6 即=6
解得=±3
所以点C坐标是(3,0)或(-3,0)
22.因为∠l=∠2(已知)
∠2=∠3(对顶角相等)
所以∠l=∠3(等量代换)
所以BD∥CE(同位角相等,两直线平行)
所以∠C=∠DBA(两直线平行,同位角相等)又因为∠C=∠D(已知)
所以∠DBA=∠D(等量代换)
所以DF∥AC(内错角相等,两直线平行)
所以∠A=∠F(两直线平行,内错角相等)
23.(本题满分10分)
解:(1)=200+0.002t
(2)=200.2厘米
(3)t=800℃
24.方案三获利最多,计算略
25.(本题满分11分)
解:(1)4h
(2)
17h
(3)建议:在9时即可加油,可以加30升.(答案不唯一)
时间:90分钟 总分:120分
一、选择题(每小题3分,共计36分)请把正确答案的序号填入表中
1.下列图形中,可用么∠1,∠AOB,∠O三种方法表示同一个角的是( )
2.如图,如果∠AOC=∠BOD,则∠AOB与∠DOC的大小关系是( )
A.∠AOB>∠DOC B.∠AOB<∠DOC C.∠AOB=∠DOC D.无法比较
3.一个游戏的中将率是1%,小花买100张奖券,下列说法正确的是()
A.一定会中奖 B.一定不中奖 C.中奖的可能性大 D.中奖的可能性小
4.从一只船上看一小岛,方向为北偏东35°,从小岛上看这只船,其方向为( )
A.南偏西35° B.南偏东55° C.北偏东55° D.北偏西35°
5.如图,下列说法中正确的是( )
A.∠1与∠C是同位角 B.∠1与∠3是同旁内角
C.∠3与∠C是内错角 D.∠1与∠3是对顶角
6.如图,根据下列条件,不能判定AB∥DF的是( )
A.∠A+∠2=180° B.∠A=∠3 C.∠1=∠4 D.∠1=∠A
7.一次函数y1=ax+b与y2=bx+a在同一直角坐标系
内的函数图像可能是
8.一次函数图象经过点A(5,3),且与直线无交点,则这个一次函数的解析式为( ).
A. B. C. D.无法确定
9.解方程组时,某同学把看错后得到,而正确的解是,那么的值是( )
A. B.不能确定,
C. D.的值不能确定
10.点、点是一次函数图像上的两点,且,则与的大小关系是( ).
A. B. C. D.不能确定
11.如图,AB∥CD,∠B=23°,∠D=42°,则∠E=( )
A.23° B.42° C.65° D.19°
12.下表是2002年3月12日《南国早报》刊登的南宁市自来水价格凋整表的一部分:
用水类别
拟调整水价(元/立方米)
一、居民生活用水
第一阶梯:月用水量0-30立方米
0.82
第二阶梯:月用水量超过30立方米的部分
1.23
调整水价后居民应缴水费(元)与月用水量(立方米)的函数图像是( )
二、填空题(每题3分,共计21分)
13.如图,OA⊥OC,OB⊥OD,垂足为O,如果∠DOC=27°,那么∠AOB=________.
14.如图中,方砖除颜色的外完全相同,小老鼠在方砖上自由走动,最终停留在白色方砖上的概率是____________.
15.如图所示,若∠A+∠2+∠3=180°,则可以判定哪两条直线平行?__________
16.如图所示,直线a∥b,c∥d,∠1=106°,则∠3=________.
17.若方程组的解中与的值相等,则a的值为________.
18.如图所示,在平面直角坐标系中,有一个三角形,三个顶点坐标分别为(4,7),(1,1),(8,3).则这个三角形的面积是________.
19.已知方程组的解是,则的解是_______.
三、解答题(共63分)
20、(1)(8分)解方程组
(2)(8分)已知方程组的解能使等式成立,求的值.
21.(本题满分8分)已知在平面直角坐标系中,点A,点B的坐标分别为A(0,0),B(0,4)点C在x轴上,且ABC的面积为6,求点C的坐标。
22.(本题满分8分)如下图所示,已知点B、E分别在AC、DF上,BD、CE均与AF相交,∠1=∠2,∠C=∠D,
求证:∠A=∠F
23.(本题满分10分)
已知金属棒的长度是温度t的一次函数,现有一根金属棒,在0℃时长度是200厘米,温度每升高1℃,它就伸长0.002厘米。
(1)求这根金属棒的长度与温度t的函数关系式;
(2)当温度为100℃时,这根金属棒的长度是多少?
(3)当这根金属棒加热后长度伸长到201.6厘米时,这根金属棒的温度是多少?
24.(10分)某地生产一种绿色蔬菜,若在市场上直接销售,每吨利润为1000元,经粗加工后销售,每吨利润可达4500元,经精加工后销售,每吨利润涨至7500元,当地一家公司收购这种蔬菜140吨,该公司加工厂的生产能力是:如果对蔬菜进行粗加工,每天可加工16吨,若果进行精加工,每天可加工6吨,但两种加工方式不能同时进行,受季节的条件限制,公司必须在15天内将这些蔬菜全部销售或加工完毕,为此公司研制了三种方案:
方案一:将蔬菜全部进行粗加工;
方案二:尽可能多的对蔬菜进行精加工,没有来得及进行加工的蔬菜,在市场上销售;
方案三:将部分蔬菜进行粗加工,其余蔬菜进行精加工,并恰好在15天内完成。
你认为选择哪种方案获利最多?为什么?
25.(本题满分11分)
“五一黄金周”的某一天,小明全家上午8时自驾小汽车从家里出发,到距离180千米的某著名旅游景点游玩.该小汽车离家的距离s(千米)与时间t(时)的关系可以用图中的曲线表示.根据图象提供的有关信息,解答下列问题:
(1)小明全家在旅游景点游玩了多少小时?
(2)求出返程途中,s(千米)与时间t(时)的函数关系,并回答小明全家到家是什么时间?
(3)若出发时汽车油箱中存油15升,该汽车的油箱总容量为35升,汽车每行驶1千米耗油升.请你就“何时加油和加油量”给小明全家提出一个合理化的建议.(加油所用时间忽略不计)
参考答案
一、选择题(每小题3分,共计36分)
1-5 BCDAC 6-10 DAAAA 11-12 CC
二、填空题(每题3分,共计21分)
13.153° 14. 15.AD∥BC
16.106° 17.a=11 18.18
19.
三、解答题(共63分)
20.(1)(说明:只有结果没有过程,不得分)
(2)解:由题意得方程组
解得
把带入方程
得
21.设点C坐标是(x,0)根据题意得,AB×AC=6 即=6
解得=±3
所以点C坐标是(3,0)或(-3,0)
22.因为∠l=∠2(已知)
∠2=∠3(对顶角相等)
所以∠l=∠3(等量代换)
所以BD∥CE(同位角相等,两直线平行)
所以∠C=∠DBA(两直线平行,同位角相等)又因为∠C=∠D(已知)
所以∠DBA=∠D(等量代换)
所以DF∥AC(内错角相等,两直线平行)
所以∠A=∠F(两直线平行,内错角相等)
23.(本题满分10分)
解:(1)=200+0.002t
(2)=200.2厘米
(3)t=800℃
24.方案三获利最多,计算略
25.(本题满分11分)
解:(1)4h
(2)
17h
(3)建议:在9时即可加油,可以加30升.(答案不唯一)
同课章节目录
