23.1图形的旋转-同步习题-2021-2022学年数学九年级上册 人教版(word版 含解析)
文档属性
| 名称 | 23.1图形的旋转-同步习题-2021-2022学年数学九年级上册 人教版(word版 含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 274.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-12-28 08:14:34 | ||
图片预览


文档简介
2021-2022学年初中数学九年级上册(人教版)
23.1图形的旋转-同步习题
时间:40分钟
一、单选题
1.下面四个图案中,是旋转对称图形的是( )
A. B. C. D.
2.在俄罗斯方块游戏中,已拼好的图案如图所示,现又出现一小方格体正向下运动,为了使所有图案消失,你必须进行以下哪项操作,才能拼成一个完整图案,使其自动消失( )
A.顺时针旋转,向右平移 B.逆时针旋转,向右平移
C.顺时针旋转,向下平移 D.逆时针旋转,向下平移
3.下列运动形式属于旋转的是( )
A.在空中上升的氢气球 B.飞驰的火车
C.时钟上钟摆的摆动 D.运动员掷出的标枪
4.如图,将三角形绕点A旋转到三角形,下列说法正确的个数有( )
(1);(2);(3);(4).
A.1个 B.2个 C.3个 D.4个
5.如图,若正方形旋转后能与正方形重合,则图形所在平面内可作为旋转中心的点共有( )个.
A.1 B.2 C.3 D.4
6.如图可以看作是由正五边形经过几次旋转得到的,则每次旋转的度数为( ).
A.72° B.90° C.108° D.144°
二、填空题
7.正六边形可以看成由基本图形________经过________次旋转而成.
8.如图,在正方形ABCD中,E为DC边上的点,连接BE,将△BCE绕点C顺时针方向旋转90°得到△DCF,连接EF,若∠BEC=60°,则∠EFD的度数为_______度.
9.如图,四边形中,,则四边形的面积为__________.
10.如图,边长为2的正三角形ABO的边OB在x轴上,将绕原点O逆时针旋转得到,则点的坐标为________.
11.如图,在平面直角坐标系中,点A的坐标为(1,4),将线段OA绕点O顺时针旋转90°得到线段OA′,则点A′的坐标是______.
三、解答题
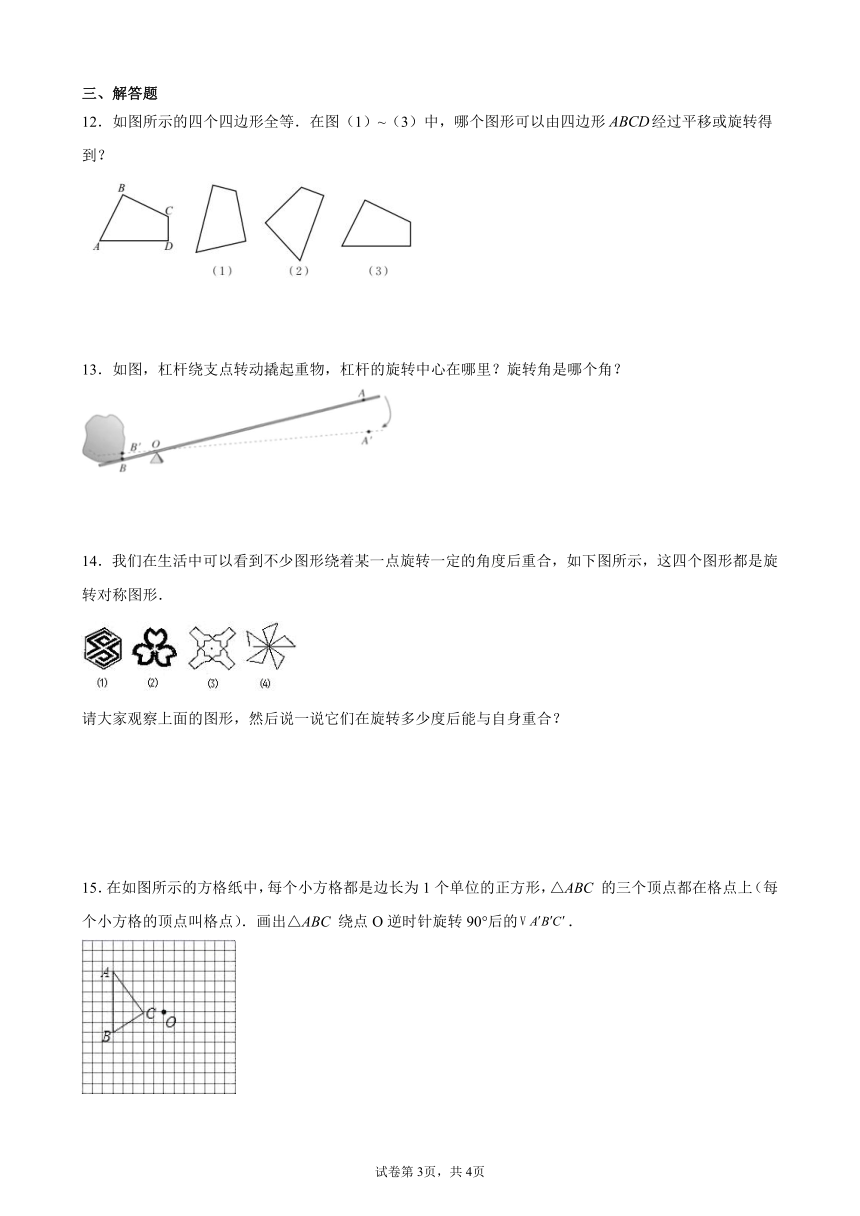
12.如图所示的四个四边形全等.在图(1)~(3)中,哪个图形可以由四边形经过平移或旋转得到?
13.如图,杠杆绕支点转动撬起重物,杠杆的旋转中心在哪里?旋转角是哪个角?
14.我们在生活中可以看到不少图形绕着某一点旋转一定的角度后重合,如下图所示,这四个图形都是旋转对称图形.
请大家观察上面的图形,然后说一说它们在旋转多少度后能与自身重合?
15.在如图所示的方格纸中,每个小方格都是边长为1个单位的正方形,△ABC 的三个顶点都在格点上(每个小方格的顶点叫格点).画出△ABC 绕点O逆时针旋转90°后的.
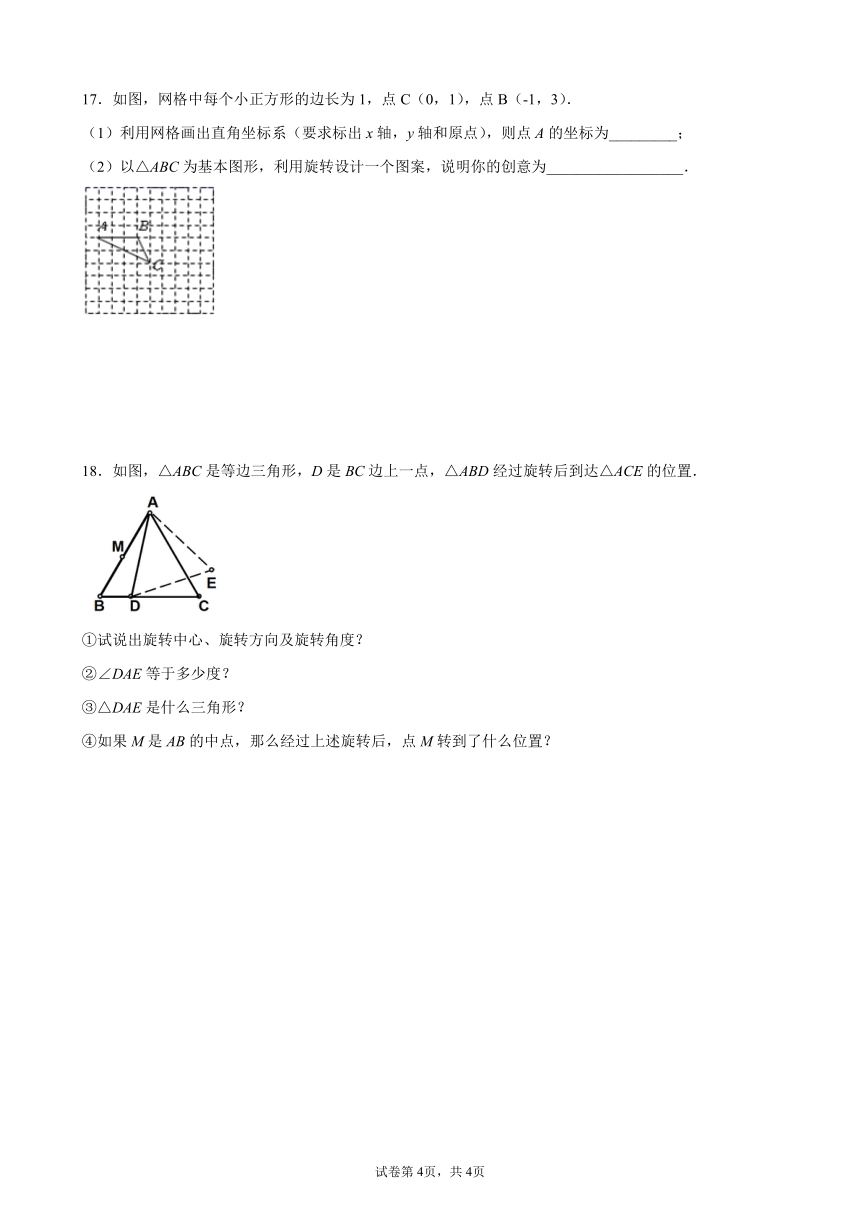
17.如图,网格中每个小正方形的边长为1,点C(0,1),点B(-1,3).
(1)利用网格画出直角坐标系(要求标出x轴,y轴和原点),则点A的坐标为_________;
(2)以△ABC为基本图形,利用旋转设计一个图案,说明你的创意为__________________.
18.如图,△ABC是等边三角形,D是BC边上一点,△ABD经过旋转后到达△ACE的位置.
①试说出旋转中心、旋转方向及旋转角度?
②∠DAE等于多少度?
③△DAE是什么三角形?
④如果M是AB的中点,那么经过上述旋转后,点M转到了什么位置?
试卷第1页,共3页
试卷第1页,共3页
参考答案
1.D
【解析】解:A、B、C不是旋转对称图形;D、是旋转对称图形.故选D.
2.A
【解析】由已知可得,顺时针旋转90°,向右平移,能把右下角完全填补.只有选项A符合条件,其他选项不能符合条件.
故选A.
3.C
【解析】在空气中上升的氢气球,飞驰的火车,运动员掷出标枪属于平移现象,时钟上钟摆的摆动属于旋转现象.
故答案选:C.
4.C
【解析】解:据旋转的性质,可知:,故(1)错误;
,故(2)正确;
,故(3)正确;
,故(4)正确.
故选:C.
5.C
【解析】以点C为旋转中心,把正方形DCEF逆时针旋转90°,可得到正方形ABCD;
以点D为旋转中心,把正方形DCEF顺时针旋转90°,可得到正方形ABCD;
以CD的中点为旋转中心,把正方形DCEF旋转180°,可得到正方形ABCD;
所以旋转中心有3个.
故选:C.
6.C
【解析】正五边形的内角是180°×(5-2)÷5=108°,所以图形是绕正五边形的顶点,经过6次顺时针旋转108°后得到的.
故选C.
7.正三角形 5
【解析】根据图形可得:正六边形可以看成由基本图形正三角形经过5次旋转而成.
8.15
【解析】∵△DCF是△BCE旋转以后得到的图形,
∴∠BEC=∠DFC=60°,∠ECF=∠BCE=90°,CF=CE.
又∵∠ECF=90°,
∴∠EFC=∠FEC=(180°﹣∠ECF)=(180°﹣90°)=45°,
故∠EFD=∠DFC﹣∠EFC=60°﹣45°=15°.
9.
【解析】解:∵CD=CB,∠DAB=∠BCD=90°,
∴将三角形CAD绕点C逆时针旋转90°,得到△CEB,
由旋转的性质可得
∴,,,,
∵∠DAB=∠BCD=90°,
∴∠D+∠ABC=180°,∠DCA+∠ACB=90°
∴∠CBE+∠ABC=180°,∠ACE=∠BCE+∠ACB=90°
∴A、B、E三点共线,
∴,
故答案为:.
11.
【解析】如图,设A1B1与x轴相交于C,
∵△ABO是等边三角形,旋转角为30°,
∴∠A1OC=60°-30°=30°,
∴A1B1⊥x轴,
∵等边△ABO的边长为2,
∴OC=×2=,
A1C=×2=1,
又∵A1在第四象限,
∴点A1的坐标为(,-1).
故答案为(,-1).
12.(4,﹣1)
【解析】由图可知A点的坐标为(1,4),根据旋转中心O,旋转方向顺时针,旋转角度90°,画图可得A′的坐标是(4, -1),故答案为: (4, -1).
13.图(2)(3)
【解析】解:图(1)是由四边形ABCD的翻折得到,
图(2)是由四边形ABCD旋转得到的,
图(3)是由四边形ABCD平移得到.
14.杠杆的旋转中心是点O,旋转角是∠BOB′(或∠AOA′)
【解析】解:杠杆绕支点转动撬起重物,杠杆绕点O旋转,所以杠杆的旋转中心是点 O,旋转角是∠BOB′(或∠AOA′).
15.见解析.
【解析】根据旋转的性质
图(1)绕着一点旋转180°后能与自身重合.
图(2)绕着一点旋转120°或240°后能与自身重合.
图(3)绕着一点旋转90°或180°或270°后能与自身重合.
图(4)绕着一点旋转72°划144°或216°或288°后能与自身重合.
16.详见解析.
【解析】如图所示即为绕点O逆时针旋转90°后.
17.A(-4,3) 见解析.
【解析】(1)直角坐标系如图所示,则A的坐标为(-4,3);
(2)如图,把△ABC绕点C顺时针旋转3次90°,180°,270°,即可得到一个风车的图案.
18.①点A、逆时针、60°;② 60°;③等边三角形;④AC边中点
【解析】略答案第1页,共2页
答案第1页,共2页
23.1图形的旋转-同步习题
时间:40分钟
一、单选题
1.下面四个图案中,是旋转对称图形的是( )
A. B. C. D.
2.在俄罗斯方块游戏中,已拼好的图案如图所示,现又出现一小方格体正向下运动,为了使所有图案消失,你必须进行以下哪项操作,才能拼成一个完整图案,使其自动消失( )
A.顺时针旋转,向右平移 B.逆时针旋转,向右平移
C.顺时针旋转,向下平移 D.逆时针旋转,向下平移
3.下列运动形式属于旋转的是( )
A.在空中上升的氢气球 B.飞驰的火车
C.时钟上钟摆的摆动 D.运动员掷出的标枪
4.如图,将三角形绕点A旋转到三角形,下列说法正确的个数有( )
(1);(2);(3);(4).
A.1个 B.2个 C.3个 D.4个
5.如图,若正方形旋转后能与正方形重合,则图形所在平面内可作为旋转中心的点共有( )个.
A.1 B.2 C.3 D.4
6.如图可以看作是由正五边形经过几次旋转得到的,则每次旋转的度数为( ).
A.72° B.90° C.108° D.144°
二、填空题
7.正六边形可以看成由基本图形________经过________次旋转而成.
8.如图,在正方形ABCD中,E为DC边上的点,连接BE,将△BCE绕点C顺时针方向旋转90°得到△DCF,连接EF,若∠BEC=60°,则∠EFD的度数为_______度.
9.如图,四边形中,,则四边形的面积为__________.
10.如图,边长为2的正三角形ABO的边OB在x轴上,将绕原点O逆时针旋转得到,则点的坐标为________.
11.如图,在平面直角坐标系中,点A的坐标为(1,4),将线段OA绕点O顺时针旋转90°得到线段OA′,则点A′的坐标是______.
三、解答题
12.如图所示的四个四边形全等.在图(1)~(3)中,哪个图形可以由四边形经过平移或旋转得到?
13.如图,杠杆绕支点转动撬起重物,杠杆的旋转中心在哪里?旋转角是哪个角?
14.我们在生活中可以看到不少图形绕着某一点旋转一定的角度后重合,如下图所示,这四个图形都是旋转对称图形.
请大家观察上面的图形,然后说一说它们在旋转多少度后能与自身重合?
15.在如图所示的方格纸中,每个小方格都是边长为1个单位的正方形,△ABC 的三个顶点都在格点上(每个小方格的顶点叫格点).画出△ABC 绕点O逆时针旋转90°后的.
17.如图,网格中每个小正方形的边长为1,点C(0,1),点B(-1,3).
(1)利用网格画出直角坐标系(要求标出x轴,y轴和原点),则点A的坐标为_________;
(2)以△ABC为基本图形,利用旋转设计一个图案,说明你的创意为__________________.
18.如图,△ABC是等边三角形,D是BC边上一点,△ABD经过旋转后到达△ACE的位置.
①试说出旋转中心、旋转方向及旋转角度?
②∠DAE等于多少度?
③△DAE是什么三角形?
④如果M是AB的中点,那么经过上述旋转后,点M转到了什么位置?
试卷第1页,共3页
试卷第1页,共3页
参考答案
1.D
【解析】解:A、B、C不是旋转对称图形;D、是旋转对称图形.故选D.
2.A
【解析】由已知可得,顺时针旋转90°,向右平移,能把右下角完全填补.只有选项A符合条件,其他选项不能符合条件.
故选A.
3.C
【解析】在空气中上升的氢气球,飞驰的火车,运动员掷出标枪属于平移现象,时钟上钟摆的摆动属于旋转现象.
故答案选:C.
4.C
【解析】解:据旋转的性质,可知:,故(1)错误;
,故(2)正确;
,故(3)正确;
,故(4)正确.
故选:C.
5.C
【解析】以点C为旋转中心,把正方形DCEF逆时针旋转90°,可得到正方形ABCD;
以点D为旋转中心,把正方形DCEF顺时针旋转90°,可得到正方形ABCD;
以CD的中点为旋转中心,把正方形DCEF旋转180°,可得到正方形ABCD;
所以旋转中心有3个.
故选:C.
6.C
【解析】正五边形的内角是180°×(5-2)÷5=108°,所以图形是绕正五边形的顶点,经过6次顺时针旋转108°后得到的.
故选C.
7.正三角形 5
【解析】根据图形可得:正六边形可以看成由基本图形正三角形经过5次旋转而成.
8.15
【解析】∵△DCF是△BCE旋转以后得到的图形,
∴∠BEC=∠DFC=60°,∠ECF=∠BCE=90°,CF=CE.
又∵∠ECF=90°,
∴∠EFC=∠FEC=(180°﹣∠ECF)=(180°﹣90°)=45°,
故∠EFD=∠DFC﹣∠EFC=60°﹣45°=15°.
9.
【解析】解:∵CD=CB,∠DAB=∠BCD=90°,
∴将三角形CAD绕点C逆时针旋转90°,得到△CEB,
由旋转的性质可得
∴,,,,
∵∠DAB=∠BCD=90°,
∴∠D+∠ABC=180°,∠DCA+∠ACB=90°
∴∠CBE+∠ABC=180°,∠ACE=∠BCE+∠ACB=90°
∴A、B、E三点共线,
∴,
故答案为:.
11.
【解析】如图,设A1B1与x轴相交于C,
∵△ABO是等边三角形,旋转角为30°,
∴∠A1OC=60°-30°=30°,
∴A1B1⊥x轴,
∵等边△ABO的边长为2,
∴OC=×2=,
A1C=×2=1,
又∵A1在第四象限,
∴点A1的坐标为(,-1).
故答案为(,-1).
12.(4,﹣1)
【解析】由图可知A点的坐标为(1,4),根据旋转中心O,旋转方向顺时针,旋转角度90°,画图可得A′的坐标是(4, -1),故答案为: (4, -1).
13.图(2)(3)
【解析】解:图(1)是由四边形ABCD的翻折得到,
图(2)是由四边形ABCD旋转得到的,
图(3)是由四边形ABCD平移得到.
14.杠杆的旋转中心是点O,旋转角是∠BOB′(或∠AOA′)
【解析】解:杠杆绕支点转动撬起重物,杠杆绕点O旋转,所以杠杆的旋转中心是点 O,旋转角是∠BOB′(或∠AOA′).
15.见解析.
【解析】根据旋转的性质
图(1)绕着一点旋转180°后能与自身重合.
图(2)绕着一点旋转120°或240°后能与自身重合.
图(3)绕着一点旋转90°或180°或270°后能与自身重合.
图(4)绕着一点旋转72°划144°或216°或288°后能与自身重合.
16.详见解析.
【解析】如图所示即为绕点O逆时针旋转90°后.
17.A(-4,3) 见解析.
【解析】(1)直角坐标系如图所示,则A的坐标为(-4,3);
(2)如图,把△ABC绕点C顺时针旋转3次90°,180°,270°,即可得到一个风车的图案.
18.①点A、逆时针、60°;② 60°;③等边三角形;④AC边中点
【解析】略答案第1页,共2页
答案第1页,共2页
同课章节目录
