23.3课题学习图案设计-同步习题-2021-2022学年数学九年级上册人教版(word版 含解析)
文档属性
| 名称 | 23.3课题学习图案设计-同步习题-2021-2022学年数学九年级上册人教版(word版 含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 621.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-12-28 08:30:39 | ||
图片预览



文档简介
2021-2022学年初中数学九年级上册(人教版)
23.3课题学习图案设计-同步习题
时间:40分钟
一、单选题
1.下列四组图形都含有两个可以重合的三角形,其中可以通过平移其中一个三角形得到另一个三角形的是( )
A. B. C. D.
2.如图是某公司的商品标志图案,则下列说法:①整个图案是按照中心对称设计的;②外部图案部分是按照轴对称设计的;③图案的外层“S”是按旋转设计的;④图案的内层“A”是按轴对称设计的.其中正确的有( )
A.1个 B.2个 C.3个 D.4个
3.边长为2的两种正方形卡片如上图①所示,卡片中的扇形半径均为2,图②是交替摆放A、B两种卡片得到的图案.若摆放这个图案共用两种卡片2021张,则这个图案中阴影部分图形的面积和为( )
A.4040 B.4044–π C.4044 D.4044+π
4.在下列四种图形变换中,如图图案包含的变换是( )
A.平移、旋转和轴对称 B.轴对称和平移
C.平移和旋转 D.旋转和轴对称
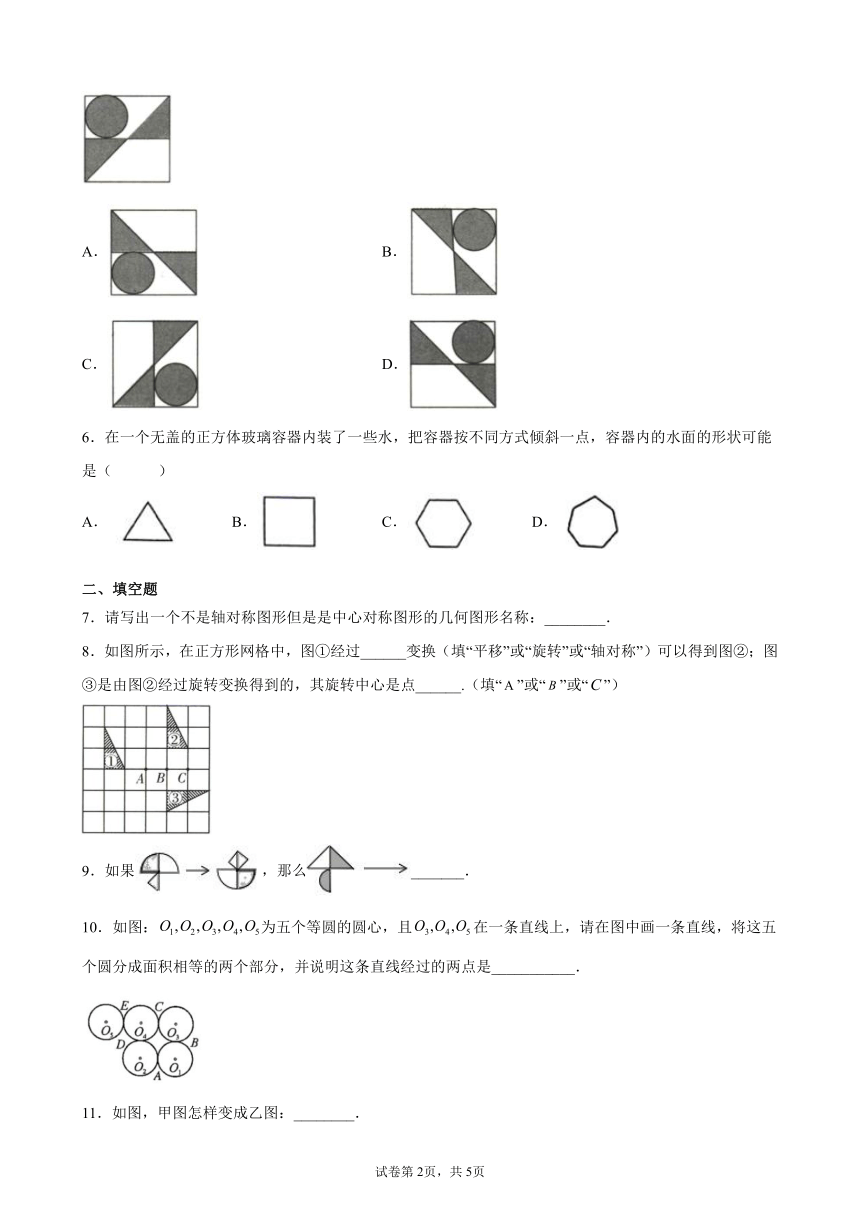
5.如图,先将该图沿着它自己的右边缘翻折,再绕着右下角的一个端点按顺时针方向旋转,之后所得到的图形是( )
A. B.
C. D.
6.在一个无盖的正方体玻璃容器内装了一些水,把容器按不同方式倾斜一点,容器内的水面的形状可能是( )
A. B. C. D.
二、填空题
7.请写出一个不是轴对称图形但是是中心对称图形的几何图形名称:________.
8.如图所示,在正方形网格中,图①经过______变换(填“平移”或“旋转”或“轴对称”)可以得到图②;图③是由图②经过旋转变换得到的,其旋转中心是点______.(填“”或“”或“”)
9.如果,那么_______.
10.如图:为五个等圆的圆心,且在一条直线上,请在图中画一条直线,将这五个圆分成面积相等的两个部分,并说明这条直线经过的两点是___________.
11.如图,甲图怎样变成乙图:________.
12.如图,第、、、…中分别有“小正方形”个、个、个、个…,则第幅图中有“小正方形”__________个.
(1) (2) (3) (4)
三、解答题
13.图中的风车图案,可以由哪个基本的图形、经过什么样的旋转得到?
14.欣赏图的图案,并分析这个图案形成的过程.
15.已知:如图甲,试用一条直线把图形分成面积相等的两部分(至少三种方法).
16.认真观察下列4个图中阴影部分构成的图案,回答下列问题:
(1)请写出这四个图案都具有的两个共同特征;
(2)请在下图中设计出你心中最美丽的图案,使它也具备你所写出的上述特征.
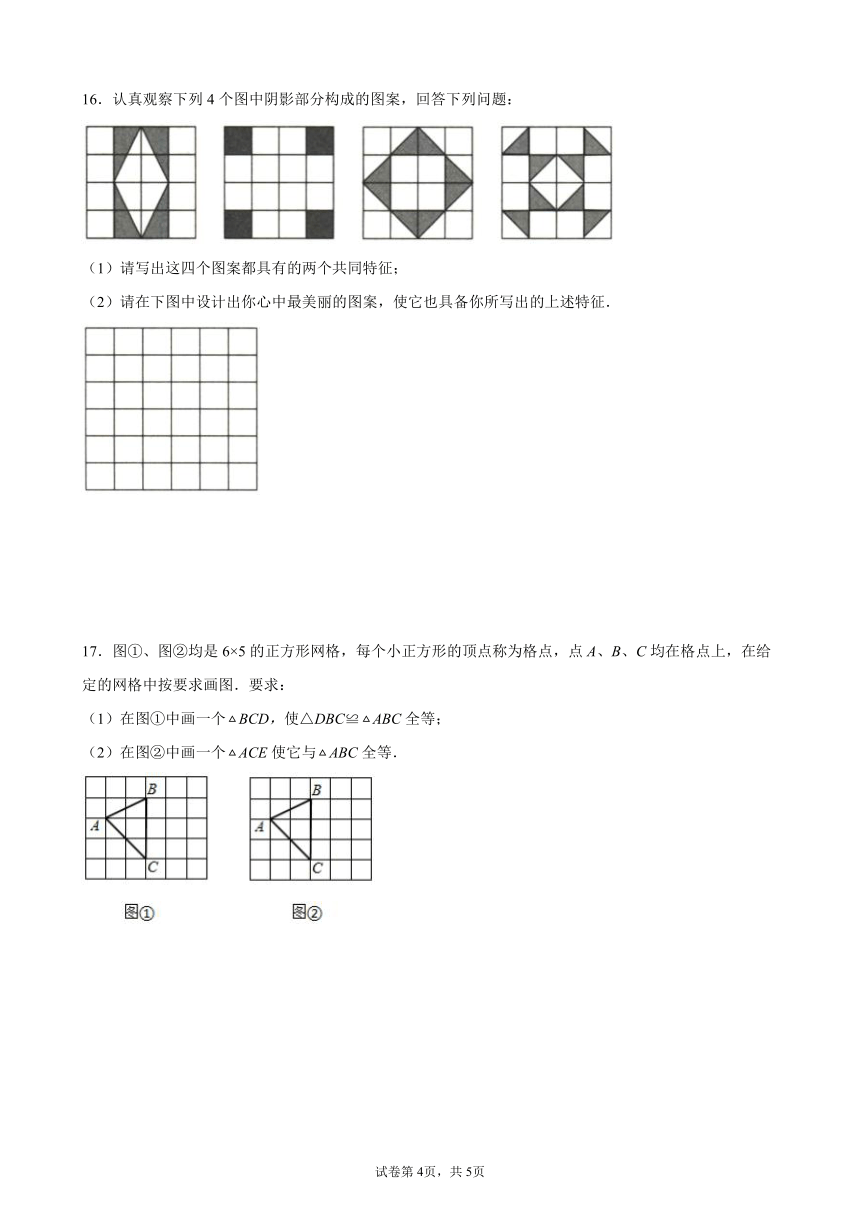
17.图①、图②均是6×5的正方形网格,每个小正方形的顶点称为格点,点A、B、C均在格点上,在给定的网格中按要求画图.要求:
(1)在图①中画一个BCD,使△DBC≌ABC全等;
(2)在图②中画一个ACE使它与ABC全等.
18.如图由长为a,宽为b的矩形、(2m+1)个长为4,宽为1的小矩形(为正整数)和若干个小圆组成,其中小圆的直径与小矩形的宽相等.
(1)当m=1时,a= ,b= ;
(2)当a=24时,求b的值;
(3)a的值能否等于30?请通过计算说明理由;
(4)直接写出a与b的数量关系.
试卷第1页,共3页
试卷第1页,共3页
参考答案
1.D
【解析】解:A、可以通过旋转或轴对称得到,故此选项错误;
B、可以通过旋转得到,故此选项错误;
C、可以通过轴对称得到,故此选项错误;
D、可通过平移得到,故此选项正确;
故选:D.
2.B
【解析】解:①整个图案内外两部分是按照不同的变换设计的,故错误;
②外部图案部分是按照旋转设计的,故错误;
③图案的外层“S”是按旋转设计的,正确;
④图案的内层“A”是按轴对称设计的,正确,
故选:B.
3.B
【解析】解:2021÷2=1010…1,
所以这个图案中阴影部分图形的面积和为:4×1010+A的阴影面积,
是:4440+4﹣π=4044﹣π.
故选:B.
4.D
【解析】解:图形的形状沿中间的竖线折叠,两部分可重合,得轴对称.
里外各一个顺时针旋转8次,得旋转.
故选:D.
5.A
【解析】先将图沿着它自己的右边缘翻折,得到,再绕着右下角的一个端点按顺时针方向旋转,之后所得到的图形为.
故选:A
6.A
【解析】解:根据题意,结合实际,容器内水面的形状不可能是正方形、六边形、七边形.
故选A.
7.平行四边形(答案不唯一)
【解析】解:根据轴对称和中心对称图形的概念,平行四边形满足要求,如图所示:
故答案为:平行四边形(答案不唯一)
8.平移
【解析】根据题意可得:图①与图②的对应点位置不变,通过平移可以得到;
根据旋转中心的确定方法是,两组对应点连线的垂直平分线的交点,可确定图②经过旋转变换得到图③的旋转中心是点A.
故填平移;A.
9..
【解析】解:由题意可知,先旋转了,上半部分再作轴对称变换,可得图形:
10.D与
【解析】点D恰好是平行四边形的中心,
则这里过D和O3即可.
故答案为:D和O3.
11.先将甲逆时针旋转度,再向左平移,就能与乙图重合.
【解析】由题意得:先将甲逆时针旋转30度,再向左平移5cm,就能与乙图重合.
故答案为先将甲逆时针旋转30度,再向左平移5cm,就能与乙图重合.
12.109
【解析】解:观察发现:
第(1)个图中有1×2-1=1个小正方形;
第(2)个图中有2×3-1=5个小正方形;
第(3)个图中有3×4-1=11个小正方形;
第(4)个图中有4×5-1=19个小正方形;
…
第(10)个图中有10×11-1=109个小正方形;
故答案为109.
13.由绕着中心经过三次逆(或顺)时针旋转90°得到.(答案不唯一).
【解析】解:图中可以将看作基本图案,图中的风车可以由绕着中心经过三次逆(或顺)时针旋转90°得到.(答案不唯一).
14.见解析
【解析】解:图中的图案是由三个“基本图案”组成的,它们分别是三种不同颜色的“爬虫”(形状、大小完全相同).在图中,同色的“爬虫”之间是平移关系,所有同色的“爬虫”可以通过其中一只经过平移而得到;相邻的不同色的“爬虫”之间可以通过旋转而得到,其中,旋转角度为120°,旋转中心为“爬虫”头上、腿上或脚趾上一点.
15.见解析
【解析】解:(1)如图所示,将图形分成两个平行四边形,分别连接两个平行四边形的对角线,产生两个交点,将两个交点连接即可得;
(2)如图所示,将图形分成两个平行四边形,分别连接两个平行四边形的对角线,产生两个交点,将两个交点连接即可得;
(3)如图所示,将不规则图形补全,然后按照(1)(2)方法,分别连接两个平行四边形的对角线,产生两个交点,将两个交点连接即可得;
16.(1)特征1:都是轴对称图形;特征2:都是中心对称图形;特征3:这些阴影图案的面积都等于4个小正方形的面积;(2)见解析
【解析】解:(1)特征1:都是轴对称图形;
特征2:都是中心对称图形;
特征3:这些阴影图案的面积都等于4个小正方形的面积;
(2)满足条件的图案有很多,这里画三个,三个都具有上述特征,如图所示:
17.(1)见解析;(2)见解析
【解析】解:(1)如图①,△BCD即为所求;
(2)如图②,△ACE即为所求.
18.(1)9,7;(2)22;(3)不能等于30,见解析;(4)
【解析】(1)长为,宽为的矩形,
当=1时,(2+1)=3,
3个长为4,宽为1的小矩形(为正整数)和5个小圆组成,
其中小圆的直径与小矩形的宽相等,
∴=3+3+1+1+1=9
=3+1+1+1+1=7
故答案为9,7;
(2)结合(1)并观察图形的变化规律可知:
=5+4,b=5+2
∴当=24时,5=20,
∴=22;
(3)不能等于30,理由如下:
∵=5+4
若=30,则5+4=30,=
∵是正整数,
∴不能等于30;
(4)结合(1)(2)可知:
,
所以与的数量关系为:.
答案第1页,共2页
答案第1页,共2页
23.3课题学习图案设计-同步习题
时间:40分钟
一、单选题
1.下列四组图形都含有两个可以重合的三角形,其中可以通过平移其中一个三角形得到另一个三角形的是( )
A. B. C. D.
2.如图是某公司的商品标志图案,则下列说法:①整个图案是按照中心对称设计的;②外部图案部分是按照轴对称设计的;③图案的外层“S”是按旋转设计的;④图案的内层“A”是按轴对称设计的.其中正确的有( )
A.1个 B.2个 C.3个 D.4个
3.边长为2的两种正方形卡片如上图①所示,卡片中的扇形半径均为2,图②是交替摆放A、B两种卡片得到的图案.若摆放这个图案共用两种卡片2021张,则这个图案中阴影部分图形的面积和为( )
A.4040 B.4044–π C.4044 D.4044+π
4.在下列四种图形变换中,如图图案包含的变换是( )
A.平移、旋转和轴对称 B.轴对称和平移
C.平移和旋转 D.旋转和轴对称
5.如图,先将该图沿着它自己的右边缘翻折,再绕着右下角的一个端点按顺时针方向旋转,之后所得到的图形是( )
A. B.
C. D.
6.在一个无盖的正方体玻璃容器内装了一些水,把容器按不同方式倾斜一点,容器内的水面的形状可能是( )
A. B. C. D.
二、填空题
7.请写出一个不是轴对称图形但是是中心对称图形的几何图形名称:________.
8.如图所示,在正方形网格中,图①经过______变换(填“平移”或“旋转”或“轴对称”)可以得到图②;图③是由图②经过旋转变换得到的,其旋转中心是点______.(填“”或“”或“”)
9.如果,那么_______.
10.如图:为五个等圆的圆心,且在一条直线上,请在图中画一条直线,将这五个圆分成面积相等的两个部分,并说明这条直线经过的两点是___________.
11.如图,甲图怎样变成乙图:________.
12.如图,第、、、…中分别有“小正方形”个、个、个、个…,则第幅图中有“小正方形”__________个.
(1) (2) (3) (4)
三、解答题
13.图中的风车图案,可以由哪个基本的图形、经过什么样的旋转得到?
14.欣赏图的图案,并分析这个图案形成的过程.
15.已知:如图甲,试用一条直线把图形分成面积相等的两部分(至少三种方法).
16.认真观察下列4个图中阴影部分构成的图案,回答下列问题:
(1)请写出这四个图案都具有的两个共同特征;
(2)请在下图中设计出你心中最美丽的图案,使它也具备你所写出的上述特征.
17.图①、图②均是6×5的正方形网格,每个小正方形的顶点称为格点,点A、B、C均在格点上,在给定的网格中按要求画图.要求:
(1)在图①中画一个BCD,使△DBC≌ABC全等;
(2)在图②中画一个ACE使它与ABC全等.
18.如图由长为a,宽为b的矩形、(2m+1)个长为4,宽为1的小矩形(为正整数)和若干个小圆组成,其中小圆的直径与小矩形的宽相等.
(1)当m=1时,a= ,b= ;
(2)当a=24时,求b的值;
(3)a的值能否等于30?请通过计算说明理由;
(4)直接写出a与b的数量关系.
试卷第1页,共3页
试卷第1页,共3页
参考答案
1.D
【解析】解:A、可以通过旋转或轴对称得到,故此选项错误;
B、可以通过旋转得到,故此选项错误;
C、可以通过轴对称得到,故此选项错误;
D、可通过平移得到,故此选项正确;
故选:D.
2.B
【解析】解:①整个图案内外两部分是按照不同的变换设计的,故错误;
②外部图案部分是按照旋转设计的,故错误;
③图案的外层“S”是按旋转设计的,正确;
④图案的内层“A”是按轴对称设计的,正确,
故选:B.
3.B
【解析】解:2021÷2=1010…1,
所以这个图案中阴影部分图形的面积和为:4×1010+A的阴影面积,
是:4440+4﹣π=4044﹣π.
故选:B.
4.D
【解析】解:图形的形状沿中间的竖线折叠,两部分可重合,得轴对称.
里外各一个顺时针旋转8次,得旋转.
故选:D.
5.A
【解析】先将图沿着它自己的右边缘翻折,得到,再绕着右下角的一个端点按顺时针方向旋转,之后所得到的图形为.
故选:A
6.A
【解析】解:根据题意,结合实际,容器内水面的形状不可能是正方形、六边形、七边形.
故选A.
7.平行四边形(答案不唯一)
【解析】解:根据轴对称和中心对称图形的概念,平行四边形满足要求,如图所示:
故答案为:平行四边形(答案不唯一)
8.平移
【解析】根据题意可得:图①与图②的对应点位置不变,通过平移可以得到;
根据旋转中心的确定方法是,两组对应点连线的垂直平分线的交点,可确定图②经过旋转变换得到图③的旋转中心是点A.
故填平移;A.
9..
【解析】解:由题意可知,先旋转了,上半部分再作轴对称变换,可得图形:
10.D与
【解析】点D恰好是平行四边形的中心,
则这里过D和O3即可.
故答案为:D和O3.
11.先将甲逆时针旋转度,再向左平移,就能与乙图重合.
【解析】由题意得:先将甲逆时针旋转30度,再向左平移5cm,就能与乙图重合.
故答案为先将甲逆时针旋转30度,再向左平移5cm,就能与乙图重合.
12.109
【解析】解:观察发现:
第(1)个图中有1×2-1=1个小正方形;
第(2)个图中有2×3-1=5个小正方形;
第(3)个图中有3×4-1=11个小正方形;
第(4)个图中有4×5-1=19个小正方形;
…
第(10)个图中有10×11-1=109个小正方形;
故答案为109.
13.由绕着中心经过三次逆(或顺)时针旋转90°得到.(答案不唯一).
【解析】解:图中可以将看作基本图案,图中的风车可以由绕着中心经过三次逆(或顺)时针旋转90°得到.(答案不唯一).
14.见解析
【解析】解:图中的图案是由三个“基本图案”组成的,它们分别是三种不同颜色的“爬虫”(形状、大小完全相同).在图中,同色的“爬虫”之间是平移关系,所有同色的“爬虫”可以通过其中一只经过平移而得到;相邻的不同色的“爬虫”之间可以通过旋转而得到,其中,旋转角度为120°,旋转中心为“爬虫”头上、腿上或脚趾上一点.
15.见解析
【解析】解:(1)如图所示,将图形分成两个平行四边形,分别连接两个平行四边形的对角线,产生两个交点,将两个交点连接即可得;
(2)如图所示,将图形分成两个平行四边形,分别连接两个平行四边形的对角线,产生两个交点,将两个交点连接即可得;
(3)如图所示,将不规则图形补全,然后按照(1)(2)方法,分别连接两个平行四边形的对角线,产生两个交点,将两个交点连接即可得;
16.(1)特征1:都是轴对称图形;特征2:都是中心对称图形;特征3:这些阴影图案的面积都等于4个小正方形的面积;(2)见解析
【解析】解:(1)特征1:都是轴对称图形;
特征2:都是中心对称图形;
特征3:这些阴影图案的面积都等于4个小正方形的面积;
(2)满足条件的图案有很多,这里画三个,三个都具有上述特征,如图所示:
17.(1)见解析;(2)见解析
【解析】解:(1)如图①,△BCD即为所求;
(2)如图②,△ACE即为所求.
18.(1)9,7;(2)22;(3)不能等于30,见解析;(4)
【解析】(1)长为,宽为的矩形,
当=1时,(2+1)=3,
3个长为4,宽为1的小矩形(为正整数)和5个小圆组成,
其中小圆的直径与小矩形的宽相等,
∴=3+3+1+1+1=9
=3+1+1+1+1=7
故答案为9,7;
(2)结合(1)并观察图形的变化规律可知:
=5+4,b=5+2
∴当=24时,5=20,
∴=22;
(3)不能等于30,理由如下:
∵=5+4
若=30,则5+4=30,=
∵是正整数,
∴不能等于30;
(4)结合(1)(2)可知:
,
所以与的数量关系为:.
答案第1页,共2页
答案第1页,共2页
同课章节目录
