2021-2022学年华东师大版九年级数学上册第二十一章二次根式 期末复习知识点分类训练(Word版含解析)
文档属性
| 名称 | 2021-2022学年华东师大版九年级数学上册第二十一章二次根式 期末复习知识点分类训练(Word版含解析) |  | |
| 格式 | doc | ||
| 文件大小 | 597.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-12-28 09:11:04 | ||
图片预览




文档简介
2021-2022学年华师大版九年级数学上册《二次根式》期末复习知识点分类训练(附答案)
一.二次根式的定义
1.下列各式中①;②; ③; ④(x≥1); ⑤;⑥一定是二次根式的有( )个.
A.3 B.4 C.5 D.6
2.当 时,是二次根式.
3.已知是整数,则满足条件的最小正整数n为 .
4.当x= 时二次根式有最小值.
二.二次根式有意义的条件
5.要使+有意义,则x应满足( )
A.≤x≤3 B.x≤3且x≠ C.<x<3 D.<x≤3
6.已知y=,则的值为( )
A. B.﹣ C. D.﹣
7.当代数式有意义时,x应满足的条件 .
8.若x,y为实数,且x=,求x﹣3+y的值.
三.二次根式的性质与化简
9.将a根号外的因式移到根号内,得( )
A. B.﹣ C.﹣ D.
10.下列变形中,正确的是( )
A.(2)2=2×3=6 B.=﹣
C.= D.=
11.实数a、b、c在数轴上的位置如图所示,化简下列代数式的值﹣+|b+c|﹣= .
四.最简二次根式
12.下列各式属于最简二次根式的是( )
A. B. C. D.
13.下列二次根式是最简二次根式的是( )
A. B. C. D.
14.已知是最简二次根式,且它与是同类二次根式,则a= .
五.二次根式的乘除法
15.化简,结果是( )
A.6x﹣6 B.﹣6x+6 C.﹣4 D.4
16.如果成立,那么( )
A.x≥0 B.x≥1 C.x>0 D.x>1
17.若成立,则( )
A.a≥0,b≥0 B.a≥0,b≤0 C.ab≥0 D.ab≤0
18.已知长方形的面积为12,其中一边长为,则另一边长为( )
A. B. C. D.
19.观察下列各式:①;②=;③,…请用含n(n≥1)的式子写出你猜想的规律: .
20.若=m,=n,则= (用含m、n的代数式表示).
六.分母有理化
21.已知a=,b=2﹣,则a与b的大小关系是( )
A.a>b B.a=b C.a<b D.不确定
22.α=﹣的倒数是 .
23.比较大小: (用>,<或=填空).
七.能合并的二次根式
24.下列根式中,不能与合并的是( )
A. B. C. D.
25.下列二次根式中,与可以合并式的是( )
A. B. C. D.
26.下列二次根式中,不能与合并的是( )
A. B. C. D.
27.若最简二次根式与最简二次根式可以合并,则x的值为( )
A.x=0 B.x=1 C.x=2 D.x=3
八.二次根式的加减法
28.若的整数部分为x,小数部分为y,则的值是( )
A. B. C.1 D.3
九.二次根式的混合运算
29.下列计算正确的是( )
A.3﹣2= B. (÷)=
C.(﹣)÷=2 D.﹣3=
30.估计的运算结果应在( )
A.6到7之间 B.7到8之间 C.8到9之间 D.9到10之间
31.计算:(﹣2)2020(+2)2021的结果是 .
32.观察下列运算过程:
请运用上面的运算方法计算:
= .
33.观察下列等式:
①3﹣2=(﹣1)2,
②5﹣2=(﹣)2,
③7﹣2=(﹣)2,…请你根据以上规律,写出第6个等式 .
34.已知a+=12,当0<a<1时,﹣= .
35.计算:.
36.计算:
(1)(3﹣)2++4.
(2)|﹣1|﹣ +(+1)2﹣()2.
(3)÷+(﹣1)0﹣1.
(4)+×﹣.
(5)()2(5+2)+5.
(6)÷﹣|2﹣3|+(﹣)﹣1.
十.二次根式的化简求值
37.已知x=,y=,则x2+xy+y2的值为( )
A.2 B.4 C.5 D.7
38.已知:m=+1,n=﹣1,则=( )
A.±3 B.﹣3 C.3 D.
39.若a=+1,则a2﹣2a+1的值为( )
A.6 B. C.﹣2 D.+2
40.如图,数轴上的点可近似表示(4﹣)÷的值是( )
A.点A B.点B C.点C D.点D
41.已知a=3﹣,b=2+,则代数式(a2﹣6a+9)(b2﹣4b+4)的值是( )
A.20 B.16 C.8 D.4
42.已知:x=(+),y=(﹣),代数式x2﹣xy+y2= .
43.已知a+=7,则= ,a﹣= .
44.若x=﹣1,则x3+x2﹣3x+2020的值为 .
45.我们将()、()称为一对“对偶式”,因为(+)(﹣)=()2﹣()2=a﹣b,所以构造“对偶式”再将其相乘可以有效的将(+)和(﹣)中的“”去掉于是二次根式除法可以这样解:如,.像这样,通过分子,分母同乘以一个式子把分母中的根号化去或把根号中的分母化去,叫做分母有理化根据以上材料,理解并运用材料提供的方法,解答以下问题:
(1)比较大小 (用“>”、“<”或“=”填空);
(2)已知x=,y=,求x2+y2的值;
(3)计算:
十一.二次根式的应用
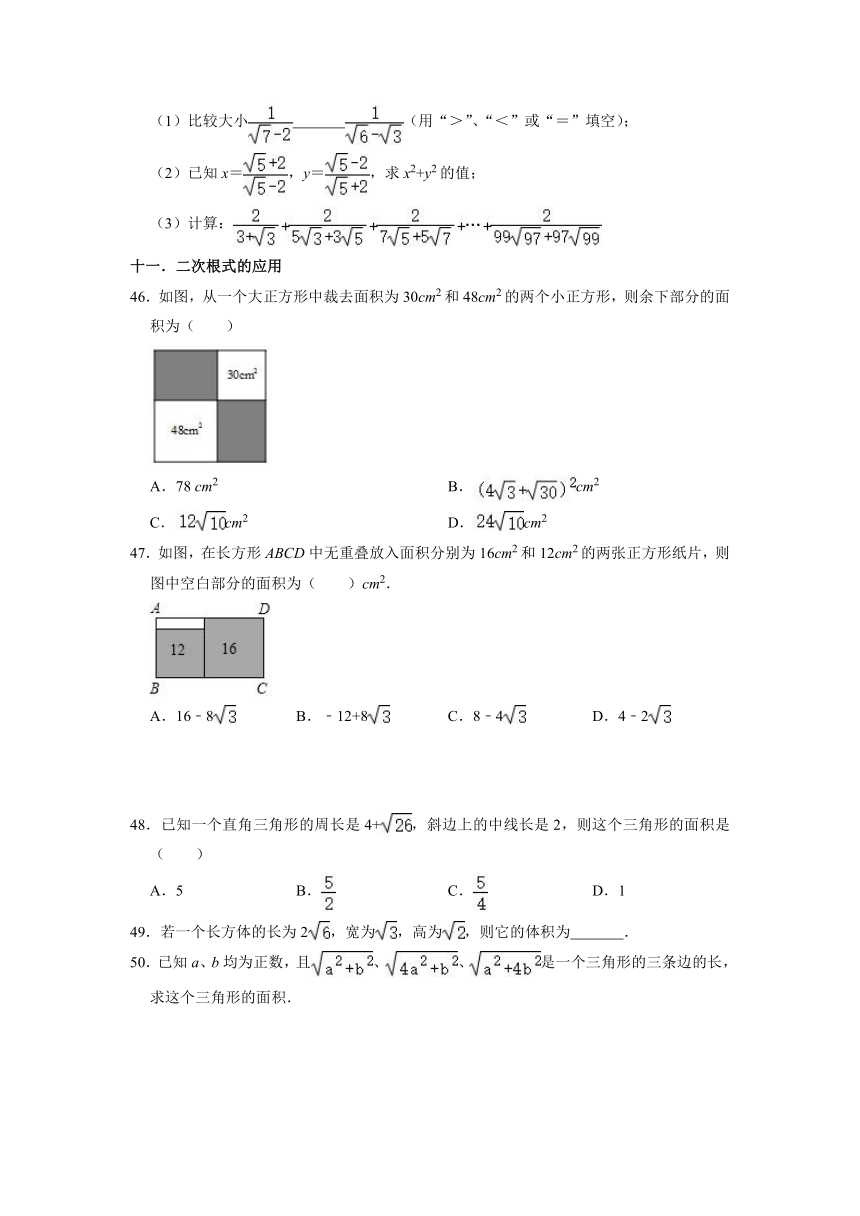
46.如图,从一个大正方形中裁去面积为30cm2和48cm2的两个小正方形,则余下部分的面积为( )
A.78 cm2 B.cm2
C.cm2 D.cm2
47.如图,在长方形ABCD中无重叠放入面积分别为16cm2和12cm2的两张正方形纸片,则图中空白部分的面积为( )cm2.
A.16﹣8 B.﹣12+8 C.8﹣4 D.4﹣2
48.已知一个直角三角形的周长是4+,斜边上的中线长是2,则这个三角形的面积是( )
A.5 B. C. D.1
49.若一个长方体的长为2,宽为,高为,则它的体积为 .
50.已知a、b均为正数,且、、是一个三角形的三条边的长,求这个三角形的面积.
参考答案
一.二次根式的定义
1.解:①符合二次根式的定义,故正确.
②无意义,故错误.
③中的a2≥0,符合二次根式的定义,故正确.
④(x≥1)中的x﹣1≥0,符合二次根式的定义,故正确.
⑤是开3次方,故错误.
⑥中的x2+2x+1=(x+1)2≥0,符合二次根式的定义,故正确.
故选:B.
2.解:∵x2≥0,
∴﹣x2≤0,
∴当x=0时,是二次根式.
3.解:∵==2,且是整数;
∴2是整数,即5n是完全平方数;
∴n的最小正整数值为5.
故答案是:5.
4.解:由题意得:2x+1=0,
解得:x=﹣,
故答案为:﹣.
二.二次根式有意义的条件
5.解:由题意得,,
解不等式①得,x≤3,
解不等式②的,x>,
所以,<x≤3.
故选:D.
6.解:由题意得,4﹣x≥0,x﹣4≥0,
解得x=4,
则y=3,
则=,
故选:C.
7.解:∵代数式有意义,
∴4﹣x≥0,x2﹣1≠0,
解得,x≤4且x≠±1,
故答案为:x≤4且x≠±1.
8.解:由题意得,y2﹣1≥0且1﹣y2≥0,
所以,y2≥1且y2≤1,
所以,y2=1,
所以,y=±1,
又∵y+1≠0,
∴y≠﹣1,
所以,y=1,
所以,x==,
x﹣3+y=()﹣3+1=8+1=9.
三.二次根式的性质与化简
9.解:a=﹣=﹣.
故选:B.
10.解;A、(2)2=12,故A错误;
B、=,故B错误;
C、=5,故C错误;
D、=,故D正确;
故选:D.
11.解:∵从数轴可知:a<b<0<c,|c|>|a|>|b|,
∴原式=|a|﹣|c﹣a+b|+|b+c|﹣b=﹣a﹣c+a﹣b+b+c﹣b=﹣b,
故答案为:﹣b.
四.最简二次根式
12.解:A、含有能开方的因数,不是最简二次根式,故本选项错误;
B、符合最简二次根式的定义,故本选项正确;
C、含有能开方的因式,不是最简二次根式,故本选项错误;
D、被开方数含分母,故本选项错误;
故选:B.
13.解:A、,故A不符合题意;
B、,故B不符合题意;
C、,故C不符合题意;
D、是最简二次根式,故D符合题意.
故选:D.
14.解:∵是最简二次根式,且它与是同类二次根式,而=4,
∴a+9=2,
∴a=﹣7,
故答案为:﹣7.
五.二次根式的乘除法
15.解:由二次根式的非负性及被开方数的非负性可得:
3x﹣5≥0
∴x≥
∴1﹣3x<0
∴
=﹣(3x﹣5)
=3x﹣1﹣3x+5
=4
故选:D.
16.解:∵成立,
∴x≥0,x﹣1>0,
解得:x>1.
故选:D.
17.解:∵成立,
∴a≥0,b≤0.
故选:B.
18.解:由题意得:12÷2===3,
故选:C.
19.解:从①②③三个式子中,
我们可以发现计算出的等号后面的系数为等号前面的根号里的整数加分数的分子,
根号里的还是原来的分数,
即=(n+1).
20.解:∵=m,=n,
∴=10 =10mn.
故答案为:10mn.
六.分母有理化
21.解:∵a===2﹣,
∴a=b.
故选:B.
22.解:==+,
故答案为:+
23.解:∵==+,
==+,
>,
∴<.
故答案为:<.
七能合并的二次根式
24.解:A、,本选项不合题意;
B、,本选项不合题意;
C、,本选项合题意;
D、,本选项不合题意;
故选:C.
25.解:A、=2,与不能合并,故本选项错误;
B、=3,与不能合并,故本选项错误;
C、=,与能合并,故本选项正确;
D、与不能合并,故本选项错误.
故选:C.
26.解:A、=2,能与合并,故此选项不符合题意;
B、=2与不是同类二次根式,不能与合并,故此选项符合题意;
C、=4,能与合并,故此选项不符合题意;
D、=6,能与合并,故此选项不符合题意;
故选:B.
27.解:∵最简二次根式与最简二次根式能合并,
∴x+3=2x,
解得:x=3,
故选:D.
八.二次根式的加减法
28.解:∵的整数部分为1,小数部分为﹣1,
∴x=1,y=﹣1,
∴=﹣(﹣1)=1.
故选:C.
九.二次根式的混合运算
29.解:A、3与﹣2不是同类二次根式,不能合并,此选项错误;
B、 (÷)= ==,此选项正确;
C、(﹣)÷=(5﹣)÷=5﹣,此选项错误;
D、﹣3=﹣2=﹣,此选项错误;
故选:B.
30.解:∵=4+,而4<<5,
∴原式运算的结果在8到9之间;
故选:C.
31.解:原式=[(﹣2)(+2)]2020 (+2)
=(5﹣4)2020 (+2)
=+2,
故答案为+2.
32.解:原式=(﹣1)+(﹣)+(﹣)+…+(﹣)+(﹣)
=(﹣1+﹣+…+﹣)
=.
故答案为.
33.解:写出第6个等式为13﹣2=(﹣)2.
故答案为13﹣2=(﹣)2.
34.解:(﹣)2=a+﹣2
=12﹣2
=10,
∵0<a<1,
∴0<<1,
∴﹣=﹣.
故答案为﹣.
35.解:原式=﹣+2
=4﹣+2
=4+.
36.解:(1)(3﹣)2++4
=9﹣6+2+4+2
=11;
(2)|﹣1|﹣ +(+1)2﹣()2
=﹣1﹣2+3+2+1﹣3
=;
(3)÷+(﹣1)0﹣1
=×+1﹣1
=5+1﹣1
=5;
(4)+×﹣
=3+﹣
=3;
(5)()2(5+2)+5
=(3﹣2+2)×(5+2)+5
=(5﹣2)×(5+2)+5
=25﹣24+5
=6;
(6)÷﹣|2﹣3|+(﹣)﹣1
=﹣(3﹣2)+(﹣2)
=﹣3+2+(﹣2)
=﹣5+.
十.二次根式的化简求值
37.解:原式=(x+y)2﹣xy
=(+)2﹣×=()2﹣=5﹣1=4.
故选:B.
38.解:∵m=,n=,
∴=8,
mn=,
∴==3,
故选:C.
39.解:a2﹣2a+1=(a﹣1)2=(+1﹣1)2=6.
故选:A.
40.解:原式=4﹣,
由于2<<3,
∴1<4﹣<2,
故选:A.
41.解:(a2﹣6a+9)(b2﹣4b+4)
=(a﹣3)2(b﹣2)2
=[(a﹣3)(b﹣2)]2
当a=3﹣,b=2+时,
原式=[(3﹣﹣3)(2+﹣2)]2
=(﹣2)2
=4.
故选:D.
42.解:∵x=(+),y=(﹣),
∴x+y=(+)+(﹣)=++﹣=2,
xy=(+)(﹣)=7﹣5=2,
∴x2﹣xy+y2
=(x+y)2﹣3xy
=(2)2﹣3×2
=28﹣6
=22,
故答案为:22.
43.解:∵a+=7,
∴=
=
=
=3;
a﹣=±=±
=±
=±3.
故答案为3;±3.
44.解:∵x=﹣1,
∴x+1=,
∴(x+1)2=2,即x2=﹣2x+1,
∴x3=﹣2x2+x
=﹣2(﹣2x+1)+x
=5x﹣2,
∴x3+x2﹣3x+2020
=5x﹣2﹣2x+1﹣3x+2020
=2019.
故答案为2019.
45.解:(1)∵==,==;
比较与
∵>,2>,
∴+2>+,
∴>.
故答案为:>.
(2)∵x2+y2=(x+y)2﹣2xy
=﹣2
=182﹣2
=324﹣2
=322
答:x2+y2的值为322.
(3)
=+++…+
=1﹣+﹣+﹣+…+﹣
=1﹣
=1﹣
答:的值为1﹣.
十一.二次根式的应用
46.解:从一个大正方形中裁去面积为30cm2和48cm2的两个小正方形,
大正方形的边长是+=(+4)cm,
留下部分(即阴影部分)的面积是(+4)2﹣30﹣48=8=24(cm2).
故选:D.
47.解:∵两张正方形纸片的面积分别为16cm2和12cm2,
∴它们的边长分别为=4cm,
=2cm,
∴AB=4cm,BC=(2+4)cm,
∴空白部分的面积=(2+4)×4﹣12﹣16,
=8+16﹣12﹣16,
=(﹣12+8)cm2.
故选:B.
48.解:设两直角边分别为a,b,斜边为c,
∵直角三角形斜边上的中线等于斜边的一半,
∴斜边c=2×2=4,
∵直角三角形的周长是4+,
∴a+b+c=4+,
∴
∴
∴ab=[(a+b)2﹣(a2+b2)]=×(26﹣16)=5,
故s三角形=ab=.
故选:B.
49.解:∵一个长方体的长为2,宽为,高为,
∴体积为:2××=2=2×6=12,
故答案为:12.
50.解:如图:
在矩形ABCD中,E、F分别为AD、AB的中点,
设AD=2b,AB=2a,
∴EF=,CE=,CF=,
∴S△CEF=S矩形ABCD﹣S△AEF﹣S△BCF﹣S△CDE=(2a) (2b)﹣ab﹣×2ba﹣×2ba=ab.
一.二次根式的定义
1.下列各式中①;②; ③; ④(x≥1); ⑤;⑥一定是二次根式的有( )个.
A.3 B.4 C.5 D.6
2.当 时,是二次根式.
3.已知是整数,则满足条件的最小正整数n为 .
4.当x= 时二次根式有最小值.
二.二次根式有意义的条件
5.要使+有意义,则x应满足( )
A.≤x≤3 B.x≤3且x≠ C.<x<3 D.<x≤3
6.已知y=,则的值为( )
A. B.﹣ C. D.﹣
7.当代数式有意义时,x应满足的条件 .
8.若x,y为实数,且x=,求x﹣3+y的值.
三.二次根式的性质与化简
9.将a根号外的因式移到根号内,得( )
A. B.﹣ C.﹣ D.
10.下列变形中,正确的是( )
A.(2)2=2×3=6 B.=﹣
C.= D.=
11.实数a、b、c在数轴上的位置如图所示,化简下列代数式的值﹣+|b+c|﹣= .
四.最简二次根式
12.下列各式属于最简二次根式的是( )
A. B. C. D.
13.下列二次根式是最简二次根式的是( )
A. B. C. D.
14.已知是最简二次根式,且它与是同类二次根式,则a= .
五.二次根式的乘除法
15.化简,结果是( )
A.6x﹣6 B.﹣6x+6 C.﹣4 D.4
16.如果成立,那么( )
A.x≥0 B.x≥1 C.x>0 D.x>1
17.若成立,则( )
A.a≥0,b≥0 B.a≥0,b≤0 C.ab≥0 D.ab≤0
18.已知长方形的面积为12,其中一边长为,则另一边长为( )
A. B. C. D.
19.观察下列各式:①;②=;③,…请用含n(n≥1)的式子写出你猜想的规律: .
20.若=m,=n,则= (用含m、n的代数式表示).
六.分母有理化
21.已知a=,b=2﹣,则a与b的大小关系是( )
A.a>b B.a=b C.a<b D.不确定
22.α=﹣的倒数是 .
23.比较大小: (用>,<或=填空).
七.能合并的二次根式
24.下列根式中,不能与合并的是( )
A. B. C. D.
25.下列二次根式中,与可以合并式的是( )
A. B. C. D.
26.下列二次根式中,不能与合并的是( )
A. B. C. D.
27.若最简二次根式与最简二次根式可以合并,则x的值为( )
A.x=0 B.x=1 C.x=2 D.x=3
八.二次根式的加减法
28.若的整数部分为x,小数部分为y,则的值是( )
A. B. C.1 D.3
九.二次根式的混合运算
29.下列计算正确的是( )
A.3﹣2= B. (÷)=
C.(﹣)÷=2 D.﹣3=
30.估计的运算结果应在( )
A.6到7之间 B.7到8之间 C.8到9之间 D.9到10之间
31.计算:(﹣2)2020(+2)2021的结果是 .
32.观察下列运算过程:
请运用上面的运算方法计算:
= .
33.观察下列等式:
①3﹣2=(﹣1)2,
②5﹣2=(﹣)2,
③7﹣2=(﹣)2,…请你根据以上规律,写出第6个等式 .
34.已知a+=12,当0<a<1时,﹣= .
35.计算:.
36.计算:
(1)(3﹣)2++4.
(2)|﹣1|﹣ +(+1)2﹣()2.
(3)÷+(﹣1)0﹣1.
(4)+×﹣.
(5)()2(5+2)+5.
(6)÷﹣|2﹣3|+(﹣)﹣1.
十.二次根式的化简求值
37.已知x=,y=,则x2+xy+y2的值为( )
A.2 B.4 C.5 D.7
38.已知:m=+1,n=﹣1,则=( )
A.±3 B.﹣3 C.3 D.
39.若a=+1,则a2﹣2a+1的值为( )
A.6 B. C.﹣2 D.+2
40.如图,数轴上的点可近似表示(4﹣)÷的值是( )
A.点A B.点B C.点C D.点D
41.已知a=3﹣,b=2+,则代数式(a2﹣6a+9)(b2﹣4b+4)的值是( )
A.20 B.16 C.8 D.4
42.已知:x=(+),y=(﹣),代数式x2﹣xy+y2= .
43.已知a+=7,则= ,a﹣= .
44.若x=﹣1,则x3+x2﹣3x+2020的值为 .
45.我们将()、()称为一对“对偶式”,因为(+)(﹣)=()2﹣()2=a﹣b,所以构造“对偶式”再将其相乘可以有效的将(+)和(﹣)中的“”去掉于是二次根式除法可以这样解:如,.像这样,通过分子,分母同乘以一个式子把分母中的根号化去或把根号中的分母化去,叫做分母有理化根据以上材料,理解并运用材料提供的方法,解答以下问题:
(1)比较大小 (用“>”、“<”或“=”填空);
(2)已知x=,y=,求x2+y2的值;
(3)计算:
十一.二次根式的应用
46.如图,从一个大正方形中裁去面积为30cm2和48cm2的两个小正方形,则余下部分的面积为( )
A.78 cm2 B.cm2
C.cm2 D.cm2
47.如图,在长方形ABCD中无重叠放入面积分别为16cm2和12cm2的两张正方形纸片,则图中空白部分的面积为( )cm2.
A.16﹣8 B.﹣12+8 C.8﹣4 D.4﹣2
48.已知一个直角三角形的周长是4+,斜边上的中线长是2,则这个三角形的面积是( )
A.5 B. C. D.1
49.若一个长方体的长为2,宽为,高为,则它的体积为 .
50.已知a、b均为正数,且、、是一个三角形的三条边的长,求这个三角形的面积.
参考答案
一.二次根式的定义
1.解:①符合二次根式的定义,故正确.
②无意义,故错误.
③中的a2≥0,符合二次根式的定义,故正确.
④(x≥1)中的x﹣1≥0,符合二次根式的定义,故正确.
⑤是开3次方,故错误.
⑥中的x2+2x+1=(x+1)2≥0,符合二次根式的定义,故正确.
故选:B.
2.解:∵x2≥0,
∴﹣x2≤0,
∴当x=0时,是二次根式.
3.解:∵==2,且是整数;
∴2是整数,即5n是完全平方数;
∴n的最小正整数值为5.
故答案是:5.
4.解:由题意得:2x+1=0,
解得:x=﹣,
故答案为:﹣.
二.二次根式有意义的条件
5.解:由题意得,,
解不等式①得,x≤3,
解不等式②的,x>,
所以,<x≤3.
故选:D.
6.解:由题意得,4﹣x≥0,x﹣4≥0,
解得x=4,
则y=3,
则=,
故选:C.
7.解:∵代数式有意义,
∴4﹣x≥0,x2﹣1≠0,
解得,x≤4且x≠±1,
故答案为:x≤4且x≠±1.
8.解:由题意得,y2﹣1≥0且1﹣y2≥0,
所以,y2≥1且y2≤1,
所以,y2=1,
所以,y=±1,
又∵y+1≠0,
∴y≠﹣1,
所以,y=1,
所以,x==,
x﹣3+y=()﹣3+1=8+1=9.
三.二次根式的性质与化简
9.解:a=﹣=﹣.
故选:B.
10.解;A、(2)2=12,故A错误;
B、=,故B错误;
C、=5,故C错误;
D、=,故D正确;
故选:D.
11.解:∵从数轴可知:a<b<0<c,|c|>|a|>|b|,
∴原式=|a|﹣|c﹣a+b|+|b+c|﹣b=﹣a﹣c+a﹣b+b+c﹣b=﹣b,
故答案为:﹣b.
四.最简二次根式
12.解:A、含有能开方的因数,不是最简二次根式,故本选项错误;
B、符合最简二次根式的定义,故本选项正确;
C、含有能开方的因式,不是最简二次根式,故本选项错误;
D、被开方数含分母,故本选项错误;
故选:B.
13.解:A、,故A不符合题意;
B、,故B不符合题意;
C、,故C不符合题意;
D、是最简二次根式,故D符合题意.
故选:D.
14.解:∵是最简二次根式,且它与是同类二次根式,而=4,
∴a+9=2,
∴a=﹣7,
故答案为:﹣7.
五.二次根式的乘除法
15.解:由二次根式的非负性及被开方数的非负性可得:
3x﹣5≥0
∴x≥
∴1﹣3x<0
∴
=﹣(3x﹣5)
=3x﹣1﹣3x+5
=4
故选:D.
16.解:∵成立,
∴x≥0,x﹣1>0,
解得:x>1.
故选:D.
17.解:∵成立,
∴a≥0,b≤0.
故选:B.
18.解:由题意得:12÷2===3,
故选:C.
19.解:从①②③三个式子中,
我们可以发现计算出的等号后面的系数为等号前面的根号里的整数加分数的分子,
根号里的还是原来的分数,
即=(n+1).
20.解:∵=m,=n,
∴=10 =10mn.
故答案为:10mn.
六.分母有理化
21.解:∵a===2﹣,
∴a=b.
故选:B.
22.解:==+,
故答案为:+
23.解:∵==+,
==+,
>,
∴<.
故答案为:<.
七能合并的二次根式
24.解:A、,本选项不合题意;
B、,本选项不合题意;
C、,本选项合题意;
D、,本选项不合题意;
故选:C.
25.解:A、=2,与不能合并,故本选项错误;
B、=3,与不能合并,故本选项错误;
C、=,与能合并,故本选项正确;
D、与不能合并,故本选项错误.
故选:C.
26.解:A、=2,能与合并,故此选项不符合题意;
B、=2与不是同类二次根式,不能与合并,故此选项符合题意;
C、=4,能与合并,故此选项不符合题意;
D、=6,能与合并,故此选项不符合题意;
故选:B.
27.解:∵最简二次根式与最简二次根式能合并,
∴x+3=2x,
解得:x=3,
故选:D.
八.二次根式的加减法
28.解:∵的整数部分为1,小数部分为﹣1,
∴x=1,y=﹣1,
∴=﹣(﹣1)=1.
故选:C.
九.二次根式的混合运算
29.解:A、3与﹣2不是同类二次根式,不能合并,此选项错误;
B、 (÷)= ==,此选项正确;
C、(﹣)÷=(5﹣)÷=5﹣,此选项错误;
D、﹣3=﹣2=﹣,此选项错误;
故选:B.
30.解:∵=4+,而4<<5,
∴原式运算的结果在8到9之间;
故选:C.
31.解:原式=[(﹣2)(+2)]2020 (+2)
=(5﹣4)2020 (+2)
=+2,
故答案为+2.
32.解:原式=(﹣1)+(﹣)+(﹣)+…+(﹣)+(﹣)
=(﹣1+﹣+…+﹣)
=.
故答案为.
33.解:写出第6个等式为13﹣2=(﹣)2.
故答案为13﹣2=(﹣)2.
34.解:(﹣)2=a+﹣2
=12﹣2
=10,
∵0<a<1,
∴0<<1,
∴﹣=﹣.
故答案为﹣.
35.解:原式=﹣+2
=4﹣+2
=4+.
36.解:(1)(3﹣)2++4
=9﹣6+2+4+2
=11;
(2)|﹣1|﹣ +(+1)2﹣()2
=﹣1﹣2+3+2+1﹣3
=;
(3)÷+(﹣1)0﹣1
=×+1﹣1
=5+1﹣1
=5;
(4)+×﹣
=3+﹣
=3;
(5)()2(5+2)+5
=(3﹣2+2)×(5+2)+5
=(5﹣2)×(5+2)+5
=25﹣24+5
=6;
(6)÷﹣|2﹣3|+(﹣)﹣1
=﹣(3﹣2)+(﹣2)
=﹣3+2+(﹣2)
=﹣5+.
十.二次根式的化简求值
37.解:原式=(x+y)2﹣xy
=(+)2﹣×=()2﹣=5﹣1=4.
故选:B.
38.解:∵m=,n=,
∴=8,
mn=,
∴==3,
故选:C.
39.解:a2﹣2a+1=(a﹣1)2=(+1﹣1)2=6.
故选:A.
40.解:原式=4﹣,
由于2<<3,
∴1<4﹣<2,
故选:A.
41.解:(a2﹣6a+9)(b2﹣4b+4)
=(a﹣3)2(b﹣2)2
=[(a﹣3)(b﹣2)]2
当a=3﹣,b=2+时,
原式=[(3﹣﹣3)(2+﹣2)]2
=(﹣2)2
=4.
故选:D.
42.解:∵x=(+),y=(﹣),
∴x+y=(+)+(﹣)=++﹣=2,
xy=(+)(﹣)=7﹣5=2,
∴x2﹣xy+y2
=(x+y)2﹣3xy
=(2)2﹣3×2
=28﹣6
=22,
故答案为:22.
43.解:∵a+=7,
∴=
=
=
=3;
a﹣=±=±
=±
=±3.
故答案为3;±3.
44.解:∵x=﹣1,
∴x+1=,
∴(x+1)2=2,即x2=﹣2x+1,
∴x3=﹣2x2+x
=﹣2(﹣2x+1)+x
=5x﹣2,
∴x3+x2﹣3x+2020
=5x﹣2﹣2x+1﹣3x+2020
=2019.
故答案为2019.
45.解:(1)∵==,==;
比较与
∵>,2>,
∴+2>+,
∴>.
故答案为:>.
(2)∵x2+y2=(x+y)2﹣2xy
=﹣2
=182﹣2
=324﹣2
=322
答:x2+y2的值为322.
(3)
=+++…+
=1﹣+﹣+﹣+…+﹣
=1﹣
=1﹣
答:的值为1﹣.
十一.二次根式的应用
46.解:从一个大正方形中裁去面积为30cm2和48cm2的两个小正方形,
大正方形的边长是+=(+4)cm,
留下部分(即阴影部分)的面积是(+4)2﹣30﹣48=8=24(cm2).
故选:D.
47.解:∵两张正方形纸片的面积分别为16cm2和12cm2,
∴它们的边长分别为=4cm,
=2cm,
∴AB=4cm,BC=(2+4)cm,
∴空白部分的面积=(2+4)×4﹣12﹣16,
=8+16﹣12﹣16,
=(﹣12+8)cm2.
故选:B.
48.解:设两直角边分别为a,b,斜边为c,
∵直角三角形斜边上的中线等于斜边的一半,
∴斜边c=2×2=4,
∵直角三角形的周长是4+,
∴a+b+c=4+,
∴
∴
∴ab=[(a+b)2﹣(a2+b2)]=×(26﹣16)=5,
故s三角形=ab=.
故选:B.
49.解:∵一个长方体的长为2,宽为,高为,
∴体积为:2××=2=2×6=12,
故答案为:12.
50.解:如图:
在矩形ABCD中,E、F分别为AD、AB的中点,
设AD=2b,AB=2a,
∴EF=,CE=,CF=,
∴S△CEF=S矩形ABCD﹣S△AEF﹣S△BCF﹣S△CDE=(2a) (2b)﹣ab﹣×2ba﹣×2ba=ab.
