人教版七年级上册数学:3.4 实际问题与一元一次方程---月历中的数学问题 课件(共30张PPT)
文档属性
| 名称 | 人教版七年级上册数学:3.4 实际问题与一元一次方程---月历中的数学问题 课件(共30张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-12-28 07:50:19 | ||
图片预览








文档简介
(共30张PPT)
月历中的数学问题
月历的相关知识
月历是指一月一页的历书,古时指史官记载下一个月所要做的政事的书册.日常生活中说的月历通常是阴历和阳历并存.
月历的相关知识
阴历是用月亮的周期来定月份的.月亮从
我们看不见它开始慢慢的长大,变成满月,
也就是圆圆的月亮,再慢慢的变小,最后再
到我们看不见它,这时就叫一个月了.所以也
叫月历.我国古代又把月亮叫太阴,所以便把
月历称为阴历.
阳历也是国际通用的公历,阳历以地球
绕太阳转一圈的时间定做一年,共365天5小
时48分46秒.平年只计365天这个整数,不计
尾数;一年分做12个月,大月31天,小月30
天,二月只有28天.四年的尾数积累起来共1
天光景,加在第四年的二月里,这一年叫做
闰年,故而闰年的二月有29天.
月历是我们日常生活中常见的一种数的排列与组合.一份完整的月历中,阴历、阳历、星期三者并存,它里面蕴含有丰富
的数学知识.
月历的相关知识
日 一 二 三 四 五 六
1 2 3 4 5 6
7 8 9 10 11 12 13
14 15 16 17 18 19 20
21 22 23 24 25 26 27
28 29 30 31
1 2 3 4 5 6
7 8 9 10 11 12 13
14 15 16 17 18 19 20
21 22 23 24 25 26 27
28 29 30 31
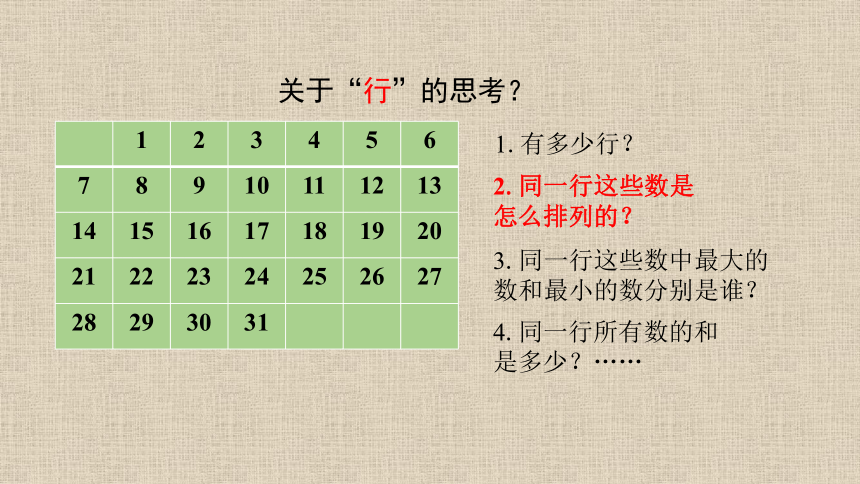
关于“行”的思考?
1.有多少行?
2.同一行这些数是
怎么排列的?
3.同一行这些数中最大的
数和最小的数分别是谁?
4.同一行所有数的和
是多少?……
1 2 3 4 5 6
7 8 9 10 11 12 13
14 15 16 17 18 19 20
21 22 23 24 25 26 27
28 29 30 31
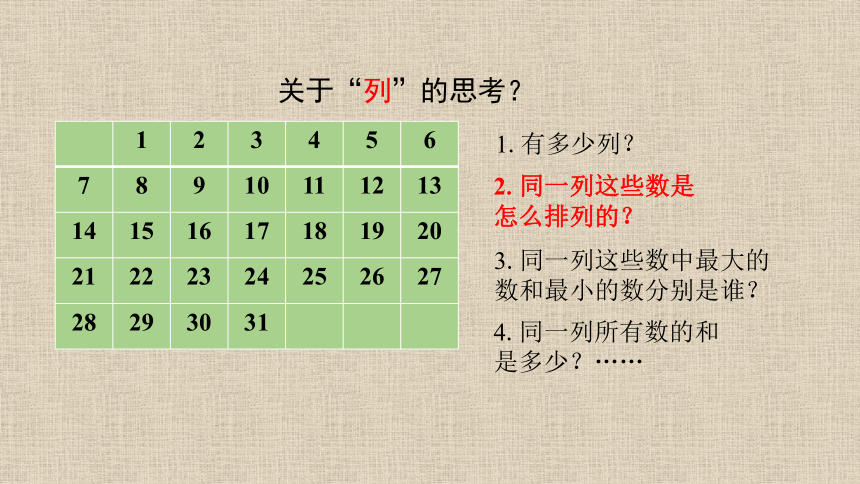
关于“列”的思考?
1.有多少列?
2.同一列这些数是
怎么排列的?
3.同一列这些数中最大的
数和最小的数分别是谁?
4.同一列所有数的和
是多少?……
1.用一个长方形的方
框框一些数来研究:
(1)框几个数?
2.尝试换一些别的图形
框框一些数来研究……
(2)研究什么?
1 2 3 4 5 6
7 8 9 10 11 12 13
14 15 16 17 18 19 20
21 22 23 24 25 26 27
28 29 30 31
关于“数与形”的思考?
1 2 3 4 5 6
7 8 9 10 11 12 13
14 15 16 17 18 19 20
21 22 23 24 25 26 27
28 29 30 31
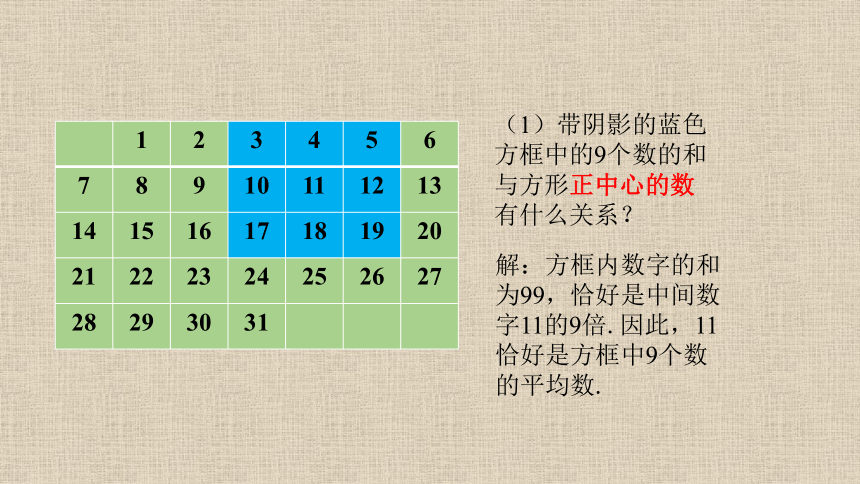
(1)带阴影的蓝色
方框中的9个数的和
与方形正中心的数
有什么关系?
解:方框内数字的和
为99,恰好是中间数
字11的9倍.因此,11
恰好是方框中9个数
的平均数.
1 2 3 4 5 6
7 8 9 10 11 12 13
14 15 16 17 18 19 20
21 22 23 24 25 26 27
28 29 30 31
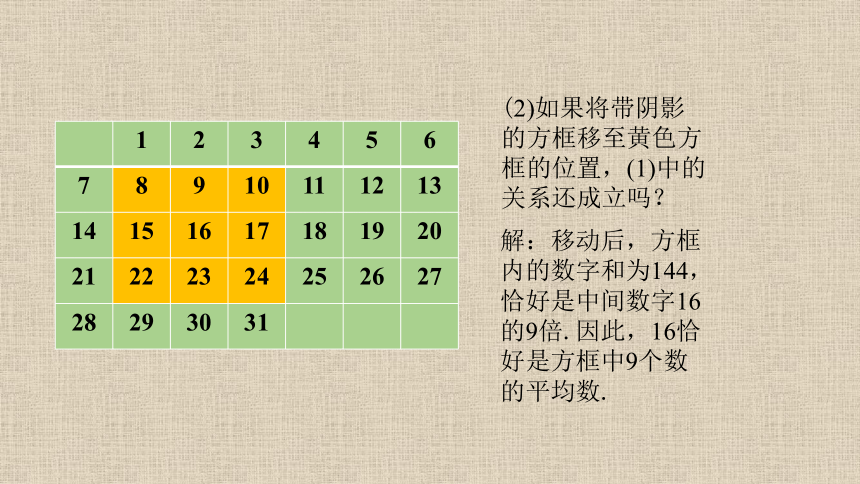
(2)如果将带阴影
的方框移至黄色方
框的位置,(1)中的
关系还成立吗?
解:移动后,方框
内的数字和为144,
恰好是中间数字16
的9倍.因此,16恰
好是方框中9个数
的平均数.
1 2 3 4 5 6
7 8 9 10 11 12 13
14 15 16 17 18 19 20
21 22 23 24 25 26 27
28 29 30 31
(3)不改变带阴影
的方框的大小,将
方框移动几个位置
试一试,你能得出
什么结论?你能证
明这个结论吗?
1 2 3 4 5 6
7 8 9 10 11 12 13
14 15 16 17 18 19 20
21 22 23 24 25 26 27
28 29 30 31
解:设方形正中心的数为x.
x
x+8
x-1
x+1
x+6
x-6
x-8
x+7
x-7
(x-8)+(x-7)+(x-6)
+(x-1)+x+(x+1)+
(x+6)+(x+7)+(x+8)
=9x.
结论:任意3×3方框
内的9个数的和都是
正中心数的9倍.
解:设方形正中心的数为x.
x
x+8
x-1
x+1
x+6
x-6
x-8
x+7
x-7
(4)这个结论对任何
一个月的月历都成立
吗?
解:仍然成立.
解:设方形正中心的数为x.
x
x+8
x-1
x+1
x+6
x-6
x-8
x+7
x-7
1 2 3 4 5 6
7 8 9 10 11 12 13
14 15 16 17 18 19 20
21 22 23 24 25 26 27
28 29 30 31
(5)如果带阴影的
蓝色方框里的数字
是4个,你能得出什
么结论?
解: 15+23=16+22;
11+19=12+18.
结论:对角线上两个
数的和相等.
1 2 3 4 5 6
7 8 9 10 11 12 13
14 15 16 17 18 19 20
21 22 23 24 25 26 27
28 29 30 31
解:设方形左上方的数为x.
x
x+8
x+7
x+1
x+(x+8)=(x+1)+(x+7).
1 2 3 4 5 6
7 8 9 10 11 12 13
14 15 16 17 18 19 20
21 22 23 24 25 26 27
28 29 30 31
(6)如图,对于蓝色
阴影的框中的4个数,
又能得出什么结论?
解:18+13=12+19.
结论:对角线上的两个
数字的和相等.
1 2 3 4 5 6
7 8 9 10 11 12 13
14 15 16 17 18 19 20
21 22 23 24 25 26 27
28 29 30 31
(7)如图,用十字形、
工字形、回字形、H形、
X形……,框出一些数
字,这里面的数字又
有哪些规律呢?大家
一起探究一下.
1 2 3 4 5 6
7 8 9 10 11 12 13
14 15 16 17 18 19 20
21 22 23 24 25 26 27
28 29 30 31
解:设十字形正中心的数为x.
x
x+1
x-1
x-7
x+7
解:设十字形正中心的数为x.
(x-7)+(x+7)+ x
(x-1)+(x+1)= 5x.
结论1:任意十字形
框内的5个数的和都
是正中心数的5倍.
x
x+1
x-1
x-7
x+7
解:设十字形正中心的数为x.
(x-7)+(x+7)+x = 3x.
结论2:任意十字形框
内的对角线上的3个数的和相等.
(x-1)+(x+1)+x = 3x.
x
x+1
x-1
x-7
x+7
1 2 3 4 5 6
7 8 9 10 11 12 13
14 15 16 17 18 19 20
21 22 23 24 25 26 27
28 29 30 31
解:设H形正中心的数为x.
x
x+1
x-1
x-6
x
x-1
x+1
x+6
x+8
x-8
解:设H形正中心的数为x.
(x-8)+(x+8)+(x-6) + x
+(x+6)+(x-1)+(x+1)= 7x.
结论1:任意H形框内
的7个数的和都是正中
心数的7倍.
x
x+1
x-1
x-6
x
x-1
x+1
x+6
x+8
x-8
解:设H形正中心的数为x.
(x-8)+(x+8)+x = 3x.
结论2:任意H形框内
的对角线上的3个数的
和都相等.
(x-6)+(x+6)+x = 3x.
x
x+1
x-1
x-6
x
x-1
x+1
x+6
x+8
x-8
解:设H形正中心的数为x.
结论3:任意H形框内,
从对角线左上到右下
看,数字依次递增8;
从对角线右上到左下
看,数字依次递增6.
……
x
x+1
x-1
x-6
x
x-1
x+1
x+6
x+8
x-8
课堂小结
1.解决本节课中的问题,
用到了什么知识?
2.解决本节课中的问题,
用到了什么思想方法?
2 4 6 8 10 12 14 16
18 20 22 24 26 28 30 32
34 36 38 40 42 44 46 48
50 52 54 56 58 60 62 64
拓展:若干个偶数排列如图所示,
探究方框中数之间的关系.
1 2 3 4 5 6
7 8 9 10 11 12 13
14 15 16 17 18 19 20
21 22 23 24 25 26 27
28 29 30 31
拓展:如图所示,框出同一直线上相邻
的三个数, 这里面的规律也很好玩,
同学们课后探究一下.
月历中的数学问题
月历的相关知识
月历是指一月一页的历书,古时指史官记载下一个月所要做的政事的书册.日常生活中说的月历通常是阴历和阳历并存.
月历的相关知识
阴历是用月亮的周期来定月份的.月亮从
我们看不见它开始慢慢的长大,变成满月,
也就是圆圆的月亮,再慢慢的变小,最后再
到我们看不见它,这时就叫一个月了.所以也
叫月历.我国古代又把月亮叫太阴,所以便把
月历称为阴历.
阳历也是国际通用的公历,阳历以地球
绕太阳转一圈的时间定做一年,共365天5小
时48分46秒.平年只计365天这个整数,不计
尾数;一年分做12个月,大月31天,小月30
天,二月只有28天.四年的尾数积累起来共1
天光景,加在第四年的二月里,这一年叫做
闰年,故而闰年的二月有29天.
月历是我们日常生活中常见的一种数的排列与组合.一份完整的月历中,阴历、阳历、星期三者并存,它里面蕴含有丰富
的数学知识.
月历的相关知识
日 一 二 三 四 五 六
1 2 3 4 5 6
7 8 9 10 11 12 13
14 15 16 17 18 19 20
21 22 23 24 25 26 27
28 29 30 31
1 2 3 4 5 6
7 8 9 10 11 12 13
14 15 16 17 18 19 20
21 22 23 24 25 26 27
28 29 30 31
关于“行”的思考?
1.有多少行?
2.同一行这些数是
怎么排列的?
3.同一行这些数中最大的
数和最小的数分别是谁?
4.同一行所有数的和
是多少?……
1 2 3 4 5 6
7 8 9 10 11 12 13
14 15 16 17 18 19 20
21 22 23 24 25 26 27
28 29 30 31
关于“列”的思考?
1.有多少列?
2.同一列这些数是
怎么排列的?
3.同一列这些数中最大的
数和最小的数分别是谁?
4.同一列所有数的和
是多少?……
1.用一个长方形的方
框框一些数来研究:
(1)框几个数?
2.尝试换一些别的图形
框框一些数来研究……
(2)研究什么?
1 2 3 4 5 6
7 8 9 10 11 12 13
14 15 16 17 18 19 20
21 22 23 24 25 26 27
28 29 30 31
关于“数与形”的思考?
1 2 3 4 5 6
7 8 9 10 11 12 13
14 15 16 17 18 19 20
21 22 23 24 25 26 27
28 29 30 31
(1)带阴影的蓝色
方框中的9个数的和
与方形正中心的数
有什么关系?
解:方框内数字的和
为99,恰好是中间数
字11的9倍.因此,11
恰好是方框中9个数
的平均数.
1 2 3 4 5 6
7 8 9 10 11 12 13
14 15 16 17 18 19 20
21 22 23 24 25 26 27
28 29 30 31
(2)如果将带阴影
的方框移至黄色方
框的位置,(1)中的
关系还成立吗?
解:移动后,方框
内的数字和为144,
恰好是中间数字16
的9倍.因此,16恰
好是方框中9个数
的平均数.
1 2 3 4 5 6
7 8 9 10 11 12 13
14 15 16 17 18 19 20
21 22 23 24 25 26 27
28 29 30 31
(3)不改变带阴影
的方框的大小,将
方框移动几个位置
试一试,你能得出
什么结论?你能证
明这个结论吗?
1 2 3 4 5 6
7 8 9 10 11 12 13
14 15 16 17 18 19 20
21 22 23 24 25 26 27
28 29 30 31
解:设方形正中心的数为x.
x
x+8
x-1
x+1
x+6
x-6
x-8
x+7
x-7
(x-8)+(x-7)+(x-6)
+(x-1)+x+(x+1)+
(x+6)+(x+7)+(x+8)
=9x.
结论:任意3×3方框
内的9个数的和都是
正中心数的9倍.
解:设方形正中心的数为x.
x
x+8
x-1
x+1
x+6
x-6
x-8
x+7
x-7
(4)这个结论对任何
一个月的月历都成立
吗?
解:仍然成立.
解:设方形正中心的数为x.
x
x+8
x-1
x+1
x+6
x-6
x-8
x+7
x-7
1 2 3 4 5 6
7 8 9 10 11 12 13
14 15 16 17 18 19 20
21 22 23 24 25 26 27
28 29 30 31
(5)如果带阴影的
蓝色方框里的数字
是4个,你能得出什
么结论?
解: 15+23=16+22;
11+19=12+18.
结论:对角线上两个
数的和相等.
1 2 3 4 5 6
7 8 9 10 11 12 13
14 15 16 17 18 19 20
21 22 23 24 25 26 27
28 29 30 31
解:设方形左上方的数为x.
x
x+8
x+7
x+1
x+(x+8)=(x+1)+(x+7).
1 2 3 4 5 6
7 8 9 10 11 12 13
14 15 16 17 18 19 20
21 22 23 24 25 26 27
28 29 30 31
(6)如图,对于蓝色
阴影的框中的4个数,
又能得出什么结论?
解:18+13=12+19.
结论:对角线上的两个
数字的和相等.
1 2 3 4 5 6
7 8 9 10 11 12 13
14 15 16 17 18 19 20
21 22 23 24 25 26 27
28 29 30 31
(7)如图,用十字形、
工字形、回字形、H形、
X形……,框出一些数
字,这里面的数字又
有哪些规律呢?大家
一起探究一下.
1 2 3 4 5 6
7 8 9 10 11 12 13
14 15 16 17 18 19 20
21 22 23 24 25 26 27
28 29 30 31
解:设十字形正中心的数为x.
x
x+1
x-1
x-7
x+7
解:设十字形正中心的数为x.
(x-7)+(x+7)+ x
(x-1)+(x+1)= 5x.
结论1:任意十字形
框内的5个数的和都
是正中心数的5倍.
x
x+1
x-1
x-7
x+7
解:设十字形正中心的数为x.
(x-7)+(x+7)+x = 3x.
结论2:任意十字形框
内的对角线上的3个数的和相等.
(x-1)+(x+1)+x = 3x.
x
x+1
x-1
x-7
x+7
1 2 3 4 5 6
7 8 9 10 11 12 13
14 15 16 17 18 19 20
21 22 23 24 25 26 27
28 29 30 31
解:设H形正中心的数为x.
x
x+1
x-1
x-6
x
x-1
x+1
x+6
x+8
x-8
解:设H形正中心的数为x.
(x-8)+(x+8)+(x-6) + x
+(x+6)+(x-1)+(x+1)= 7x.
结论1:任意H形框内
的7个数的和都是正中
心数的7倍.
x
x+1
x-1
x-6
x
x-1
x+1
x+6
x+8
x-8
解:设H形正中心的数为x.
(x-8)+(x+8)+x = 3x.
结论2:任意H形框内
的对角线上的3个数的
和都相等.
(x-6)+(x+6)+x = 3x.
x
x+1
x-1
x-6
x
x-1
x+1
x+6
x+8
x-8
解:设H形正中心的数为x.
结论3:任意H形框内,
从对角线左上到右下
看,数字依次递增8;
从对角线右上到左下
看,数字依次递增6.
……
x
x+1
x-1
x-6
x
x-1
x+1
x+6
x+8
x-8
课堂小结
1.解决本节课中的问题,
用到了什么知识?
2.解决本节课中的问题,
用到了什么思想方法?
2 4 6 8 10 12 14 16
18 20 22 24 26 28 30 32
34 36 38 40 42 44 46 48
50 52 54 56 58 60 62 64
拓展:若干个偶数排列如图所示,
探究方框中数之间的关系.
1 2 3 4 5 6
7 8 9 10 11 12 13
14 15 16 17 18 19 20
21 22 23 24 25 26 27
28 29 30 31
拓展:如图所示,框出同一直线上相邻
的三个数, 这里面的规律也很好玩,
同学们课后探究一下.
