人教版七年级上册数学 第三章一元一次方程 3.4实际问题与一元一次方程(七)(共20张)
文档属性
| 名称 | 人教版七年级上册数学 第三章一元一次方程 3.4实际问题与一元一次方程(七)(共20张) |  | |
| 格式 | pptx | ||
| 文件大小 | 622.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-12-28 11:14:45 | ||
图片预览







文档简介
(共20张PPT)
实际问题与一元一次方程(七)
行程问题的三个基本量:时间、速度、路程;
基本关系:路程=速度时间;
变形关系:速度=路程时间;
时间=路程
已知三个基本量中的两个,利用基本关系及变形关系可以求出另一个.
复习引入
练习:
(1)已知速度为 千米/时,时间为 小时,则路程为_____________千米;
(2)已知时间为 小时,路程为 千米,则速
度为___________千米/时;
(3)已知速度为 千米/时,路程为( )千米,
则时间为__________小时.
两个阶段:相遇前和相遇后;
两个研究对象:小刚和小强;
基本关系:路程=速度时间.
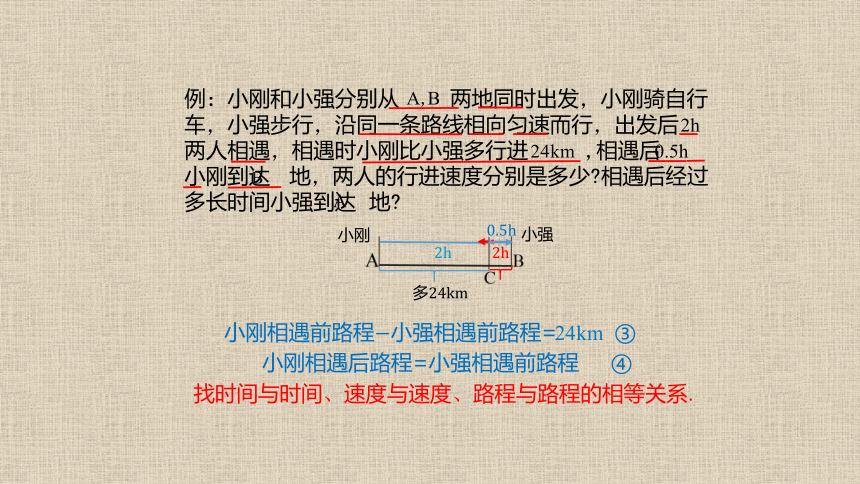
例:小刚和小强分别从 两地同时出发,小刚骑自行车,小强步行,沿同一条路线相向匀速而行,出发后 两人相遇,相遇时小刚比小强多行进 ,相遇后 小刚到达 地,两人的行进速度分别是多少 相遇后经过多长时间小强到达 地
例题讲解
例:小刚和小强分别从 两地同时出发,小刚骑自行车,小强步行,沿同一条路线相向匀速而行,出发后 两人相遇,相遇时小刚比小强多行进 ,相遇后 小刚到达 地,两人的行进速度分别是多少 相遇后经过多长时间小强到达 地
小刚相遇前速度=小刚相遇后速度①
小刚
小强
小刚
小强
小刚相遇前路程+小强相遇前路程= 两地距离②
例:小刚和小强分别从 两地同时出发,小刚骑自行车,小强步行,沿同一条路线相向匀速而行,出发后 两人相遇,相遇时小刚比小强多行进 ,相遇后 小刚到达 地,两人的行进速度分别是多少 相遇后经过多长时间小强到达 地
小刚相遇后路程=小强相遇前路程 ④
找时间与时间、速度与速度、路程与路程的相等关系.
小刚相遇前路程小强相遇前路程= ③
多
小刚
小强
小刚相遇前速度=小刚相遇后速度 ①
小刚相遇后路程=小强相遇前路程 ④
√
√
√
√
相遇前 相遇后
时间 速度 路程 时间 速度 路程
小刚
小强
(方法1):设小强的速度为. .
小刚相遇前路程小强相遇前路程= ③
小刚相遇前路程=小刚相遇前速度 ⑤
小强相遇前路程=小强相遇前速度 ⑥
小刚相遇后路程=小刚相遇后速度 ⑦
多
小刚
小强
√
小刚相遇前路程+小强相遇前路程= 两地距离 ②
小刚相遇前速度=小刚相遇后速度 ①
小刚相遇后路程=小强相遇前路程 ④
√
√
√
√
√
相遇前 相遇后
时间 速度 路程 时间 速度 路程
小刚
小强
小刚相遇前路程小强相遇前路程= ③
小刚相遇前路程=小刚相遇前速度 ⑤
小强相遇前路程=小强相遇前速度 ⑥
小刚相遇后路程=小刚相遇后速度 ⑦
(方法2):设小强的速度 .
多
小刚
小强
小刚相遇前速度=小刚相遇后速度 ①
小刚相遇后路程=小强相遇前路程 ④
√
√
√
√
√
相遇前 相遇后
时间 速度 路程 时间 速度 路程
小刚
小强
小刚相遇前路程=小刚相遇前速度 ⑤
小强相遇前路程=小强相遇前速度 ⑥
小刚相遇后路程=小刚相遇后速度 ⑦
小刚相遇前路程小强相遇前路程= ③
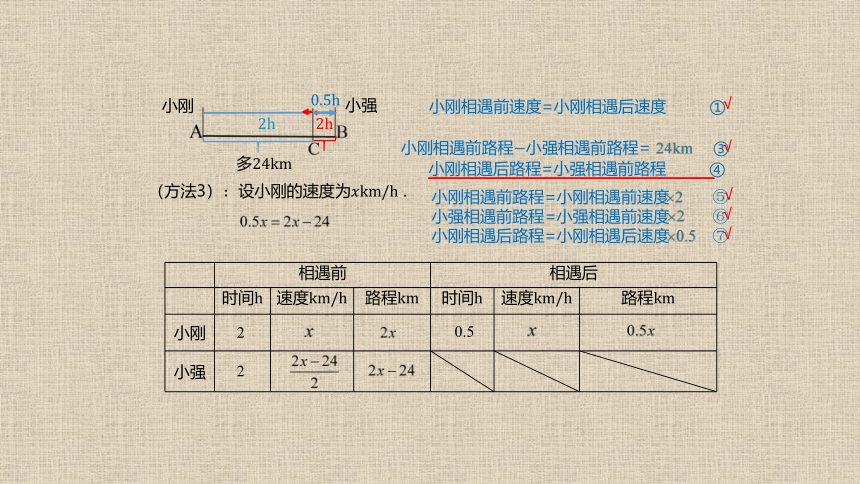
(方法3):设小刚的速度为 .
多
小刚
小强
根据“小刚相遇后的路程=小强相遇前的路程”得方程:
相遇前 相遇后
时间 速度 路程 时间 速度 路程
小刚
小强
(方法3)解:设小刚的速度为
则小刚相遇前行驶路程为 ,小强相遇前行驶路程为
,小刚相遇后的路程为
.
检验 是方程的解,符合实际情况.
小强的速度为 (km/h),
解方程,得
,
,
.
答:小刚的速度为16 km/h,小强的速度为4km/h,
相遇后经过8小时小强到达A地.
小强相遇后到达A地的时间为 ,
相遇点C与A的距离为 ,
(2)相等关系:题目中隐含的时间、速度、路程关系,以及研究对象每个运动阶段的基本关系.
(1)画线段图反映运动过程.
(3)有几个未知量就要找出几个含这些未知量的相等关系.
课堂小结
(5)从实际问题到列出方程这个过程是难点,完成这个过程的步骤和方法如下:
(4)用表格整理题目所有涉及的量,设恰当未知量,用合适的相等关系列方程.
用表格整理所有量,
设一个字母表示某一个未知量,用含该字母的式子表示其他未知量.
第一遍读题,理解题目背景,明确研究对象、阶段、基本量.
第二遍读题(逐句),
(画图)找同类量之间相等关系,基本量 之间相等关系.
检查相等关系漏、重.
列方程
(将相等关系中的量用已知数或含字母的式子表示)
思考练习
一辆卡车从甲地匀速开往乙地,出发2小时后,一辆轿车从甲地出发去追这辆卡车,轿车的速度比卡车的速度快30千米每小时,但轿车行驶一个小时后突遇故障,修理15分钟后,又上路追这辆卡车,但速度减小了 ,结果用两个小时才追上这辆卡车,求卡车的速度,只列出方程.
两个研究对象:卡车和轿车;
基本关系:路程=速度时间.
轿车两个阶段:故障前和故障后;
轿车
乙
卡车
甲
轿车故障前的速度=卡车速度+千米每小时①
一辆卡车从甲地匀速开往乙地,出发2小时后,一辆轿车从甲地出发去追这辆卡车,轿车的速度比卡车的速度快30千米每小时,但轿车行驶一个小时后突遇故障,修理15分钟后,又上路追这辆卡车,但速度减小了 ,结果用两个小时才追上这辆卡车,求卡车的速度,只列出方程.
轿车故障后的速度=轿车故障前速度 ②
一辆卡车从甲地匀速开往乙地,出发2小时后,一辆轿车从甲地出发去追这辆卡车,轿车的速度比卡车的速度快30千米每小时,但轿车行驶一个小时后突遇故障,修理15分钟后,又上路追这辆卡车,但速度减小了 ,结果用两个小时才追上这辆卡车,求卡车的速度,只列出方程.
轿车
乙
卡车
甲
轿车故障前路程+轿车故障后路程=卡车全程③
轿车
乙
卡车
甲
卡车全程=卡车速度 ④
轿车故障前路程=轿车故障前速度1 ⑤
轿车故障后路程=轿车故障后速度⑥
一辆卡车从甲地匀速开往乙地,出发2小时后,一辆轿车从甲地出发去追这辆卡车,轿车的速度比卡车的速度快30千米每小时,但轿车行驶一个小时后突遇故障,修理15分钟后,又上路追这辆卡车,但速度减小了 ,结果用两个小时才追上这辆卡车,求卡车的速度,只列出方程.
轿车故障前的速度=卡车速度+30千米每小时①
轿车故障后的速度=轿车故障前速度 ②
轿车故障前路程+轿车故障后路程=卡车全程③
轿车
乙
卡车
甲
卡车全程=卡车速度 ④
轿车故障前路程=轿车故障前速度1 ⑤
轿车故障后路程=轿车故障后速度⑥
时间 速度 路程
轿车 故障前
故障后
卡车 (全程)
1
2
(方法1)设卡车速度为.
√
√
√
√
√
轿车故障前的速度=卡车速度+30千米每小时①
轿车故障后的速度=轿车故障前速度 ②
轿车故障前路程+轿车故障后路程=卡车全程③
轿车
乙
卡车
甲
卡车全程=卡车速度 ④
轿车故障前路程=轿车故障前速度1 ⑤
轿车故障后路程=轿车故障后速度⑥
时间 速度 路程
轿车 故障前
故障后
卡车 (全程)
1
2
(方法2) 轿车故障前速度为.
√
√
√
√
√
实际问题与一元一次方程(七)
行程问题的三个基本量:时间、速度、路程;
基本关系:路程=速度时间;
变形关系:速度=路程时间;
时间=路程
已知三个基本量中的两个,利用基本关系及变形关系可以求出另一个.
复习引入
练习:
(1)已知速度为 千米/时,时间为 小时,则路程为_____________千米;
(2)已知时间为 小时,路程为 千米,则速
度为___________千米/时;
(3)已知速度为 千米/时,路程为( )千米,
则时间为__________小时.
两个阶段:相遇前和相遇后;
两个研究对象:小刚和小强;
基本关系:路程=速度时间.
例:小刚和小强分别从 两地同时出发,小刚骑自行车,小强步行,沿同一条路线相向匀速而行,出发后 两人相遇,相遇时小刚比小强多行进 ,相遇后 小刚到达 地,两人的行进速度分别是多少 相遇后经过多长时间小强到达 地
例题讲解
例:小刚和小强分别从 两地同时出发,小刚骑自行车,小强步行,沿同一条路线相向匀速而行,出发后 两人相遇,相遇时小刚比小强多行进 ,相遇后 小刚到达 地,两人的行进速度分别是多少 相遇后经过多长时间小强到达 地
小刚相遇前速度=小刚相遇后速度①
小刚
小强
小刚
小强
小刚相遇前路程+小强相遇前路程= 两地距离②
例:小刚和小强分别从 两地同时出发,小刚骑自行车,小强步行,沿同一条路线相向匀速而行,出发后 两人相遇,相遇时小刚比小强多行进 ,相遇后 小刚到达 地,两人的行进速度分别是多少 相遇后经过多长时间小强到达 地
小刚相遇后路程=小强相遇前路程 ④
找时间与时间、速度与速度、路程与路程的相等关系.
小刚相遇前路程小强相遇前路程= ③
多
小刚
小强
小刚相遇前速度=小刚相遇后速度 ①
小刚相遇后路程=小强相遇前路程 ④
√
√
√
√
相遇前 相遇后
时间 速度 路程 时间 速度 路程
小刚
小强
(方法1):设小强的速度为. .
小刚相遇前路程小强相遇前路程= ③
小刚相遇前路程=小刚相遇前速度 ⑤
小强相遇前路程=小强相遇前速度 ⑥
小刚相遇后路程=小刚相遇后速度 ⑦
多
小刚
小强
√
小刚相遇前路程+小强相遇前路程= 两地距离 ②
小刚相遇前速度=小刚相遇后速度 ①
小刚相遇后路程=小强相遇前路程 ④
√
√
√
√
√
相遇前 相遇后
时间 速度 路程 时间 速度 路程
小刚
小强
小刚相遇前路程小强相遇前路程= ③
小刚相遇前路程=小刚相遇前速度 ⑤
小强相遇前路程=小强相遇前速度 ⑥
小刚相遇后路程=小刚相遇后速度 ⑦
(方法2):设小强的速度 .
多
小刚
小强
小刚相遇前速度=小刚相遇后速度 ①
小刚相遇后路程=小强相遇前路程 ④
√
√
√
√
√
相遇前 相遇后
时间 速度 路程 时间 速度 路程
小刚
小强
小刚相遇前路程=小刚相遇前速度 ⑤
小强相遇前路程=小强相遇前速度 ⑥
小刚相遇后路程=小刚相遇后速度 ⑦
小刚相遇前路程小强相遇前路程= ③
(方法3):设小刚的速度为 .
多
小刚
小强
根据“小刚相遇后的路程=小强相遇前的路程”得方程:
相遇前 相遇后
时间 速度 路程 时间 速度 路程
小刚
小强
(方法3)解:设小刚的速度为
则小刚相遇前行驶路程为 ,小强相遇前行驶路程为
,小刚相遇后的路程为
.
检验 是方程的解,符合实际情况.
小强的速度为 (km/h),
解方程,得
,
,
.
答:小刚的速度为16 km/h,小强的速度为4km/h,
相遇后经过8小时小强到达A地.
小强相遇后到达A地的时间为 ,
相遇点C与A的距离为 ,
(2)相等关系:题目中隐含的时间、速度、路程关系,以及研究对象每个运动阶段的基本关系.
(1)画线段图反映运动过程.
(3)有几个未知量就要找出几个含这些未知量的相等关系.
课堂小结
(5)从实际问题到列出方程这个过程是难点,完成这个过程的步骤和方法如下:
(4)用表格整理题目所有涉及的量,设恰当未知量,用合适的相等关系列方程.
用表格整理所有量,
设一个字母表示某一个未知量,用含该字母的式子表示其他未知量.
第一遍读题,理解题目背景,明确研究对象、阶段、基本量.
第二遍读题(逐句),
(画图)找同类量之间相等关系,基本量 之间相等关系.
检查相等关系漏、重.
列方程
(将相等关系中的量用已知数或含字母的式子表示)
思考练习
一辆卡车从甲地匀速开往乙地,出发2小时后,一辆轿车从甲地出发去追这辆卡车,轿车的速度比卡车的速度快30千米每小时,但轿车行驶一个小时后突遇故障,修理15分钟后,又上路追这辆卡车,但速度减小了 ,结果用两个小时才追上这辆卡车,求卡车的速度,只列出方程.
两个研究对象:卡车和轿车;
基本关系:路程=速度时间.
轿车两个阶段:故障前和故障后;
轿车
乙
卡车
甲
轿车故障前的速度=卡车速度+千米每小时①
一辆卡车从甲地匀速开往乙地,出发2小时后,一辆轿车从甲地出发去追这辆卡车,轿车的速度比卡车的速度快30千米每小时,但轿车行驶一个小时后突遇故障,修理15分钟后,又上路追这辆卡车,但速度减小了 ,结果用两个小时才追上这辆卡车,求卡车的速度,只列出方程.
轿车故障后的速度=轿车故障前速度 ②
一辆卡车从甲地匀速开往乙地,出发2小时后,一辆轿车从甲地出发去追这辆卡车,轿车的速度比卡车的速度快30千米每小时,但轿车行驶一个小时后突遇故障,修理15分钟后,又上路追这辆卡车,但速度减小了 ,结果用两个小时才追上这辆卡车,求卡车的速度,只列出方程.
轿车
乙
卡车
甲
轿车故障前路程+轿车故障后路程=卡车全程③
轿车
乙
卡车
甲
卡车全程=卡车速度 ④
轿车故障前路程=轿车故障前速度1 ⑤
轿车故障后路程=轿车故障后速度⑥
一辆卡车从甲地匀速开往乙地,出发2小时后,一辆轿车从甲地出发去追这辆卡车,轿车的速度比卡车的速度快30千米每小时,但轿车行驶一个小时后突遇故障,修理15分钟后,又上路追这辆卡车,但速度减小了 ,结果用两个小时才追上这辆卡车,求卡车的速度,只列出方程.
轿车故障前的速度=卡车速度+30千米每小时①
轿车故障后的速度=轿车故障前速度 ②
轿车故障前路程+轿车故障后路程=卡车全程③
轿车
乙
卡车
甲
卡车全程=卡车速度 ④
轿车故障前路程=轿车故障前速度1 ⑤
轿车故障后路程=轿车故障后速度⑥
时间 速度 路程
轿车 故障前
故障后
卡车 (全程)
1
2
(方法1)设卡车速度为.
√
√
√
√
√
轿车故障前的速度=卡车速度+30千米每小时①
轿车故障后的速度=轿车故障前速度 ②
轿车故障前路程+轿车故障后路程=卡车全程③
轿车
乙
卡车
甲
卡车全程=卡车速度 ④
轿车故障前路程=轿车故障前速度1 ⑤
轿车故障后路程=轿车故障后速度⑥
时间 速度 路程
轿车 故障前
故障后
卡车 (全程)
1
2
(方法2) 轿车故障前速度为.
√
√
√
√
√
