人教版七年级上册数学第三章一元一次方程 3.4实际问题与一元一次方程(四)(共27张)
文档属性
| 名称 | 人教版七年级上册数学第三章一元一次方程 3.4实际问题与一元一次方程(四)(共27张) |  | |
| 格式 | pptx | ||
| 文件大小 | 455.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-12-28 12:19:18 | ||
图片预览





文档简介
(共27张PPT)
实际问题与一元一次方程(四)
学习新知
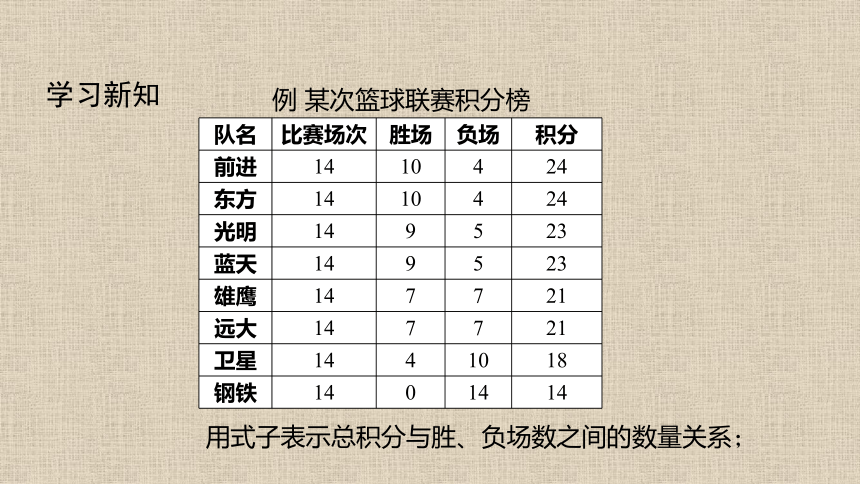
例 某次篮球联赛积分榜
用式子表示总积分与胜、负场数之间的数量关系;
队名 比赛场次 胜场 负场 积分
前进 14 10 4 24
东方 14 10 4 24
光明 14 9 5 23
蓝天 14 9 5 23
雄鹰 14 7 7 21
远大 14 7 7 21
卫星 14 4 10 18
钢铁 14 0 14 14
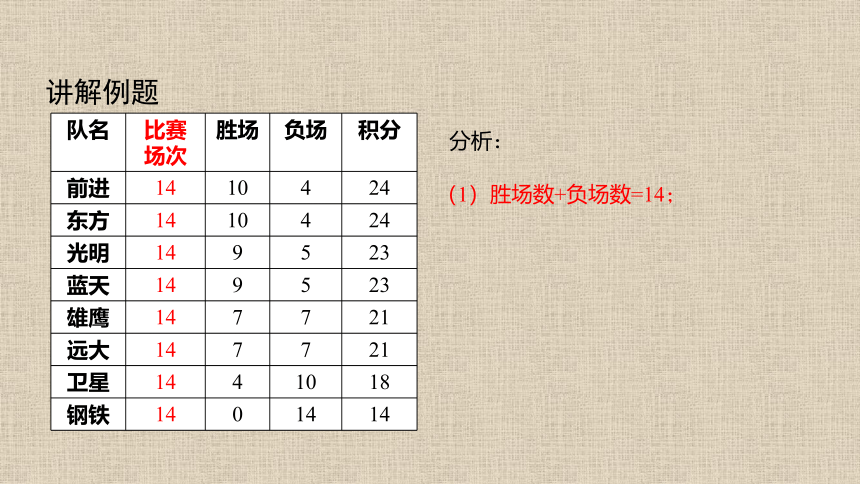
讲解例题
(1)胜场数+负场数=14;
分析:
队名 比赛 场次 胜场 负场 积分
前进 14 10 4 24
东方 14 10 4 24
光明 14 9 5 23
蓝天 14 9 5 23
雄鹰 14 7 7 21
远大 14 7 7 21
卫星 14 4 10 18
钢铁 14 0 14 14
(1)胜场数+负场数=14;
分析:
队名 比赛 场次 胜场 负场 积分
前进 14 10 4 24
东方 14 10 4 24
光明 14 9 5 23
蓝天 14 9 5 23
雄鹰 14 7 7 21
远大 14 7 7 21
卫星 14 4 10 18
钢铁 14 0 14 14
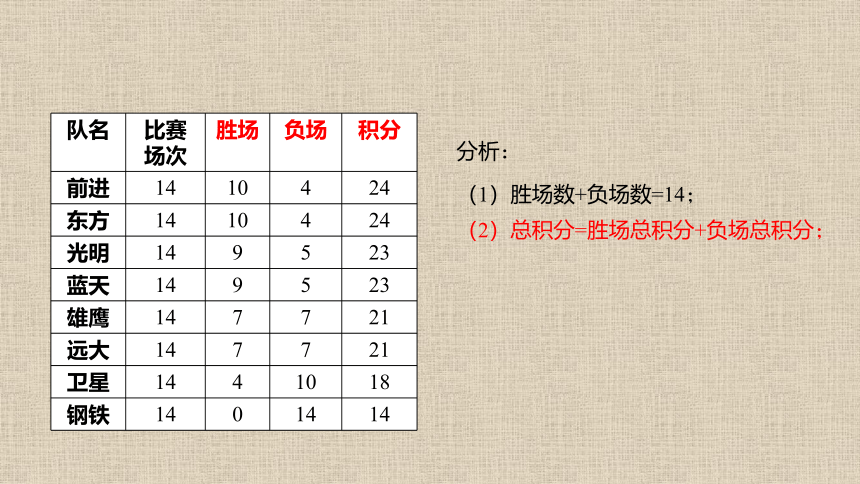
(2)总积分=胜场总积分+负场总积分;
(1)胜场数+负场数=14;
分析:
(2)总积分=胜场总积分+负场总积分;
(3)胜场总积分=×胜场数
负场总积分=×负场数.
队名 比赛 场次 胜场 负场 积分
前进 14 10 4 24
东方 14 10 4 24
光明 14 9 5 23
蓝天 14 9 5 23
雄鹰 14 7 7 21
远大 14 7 7 21
卫星 14 4 10 18
钢铁 14 0 14 14
(3)胜场总积分=×胜场数
负场总积分=×负场数.
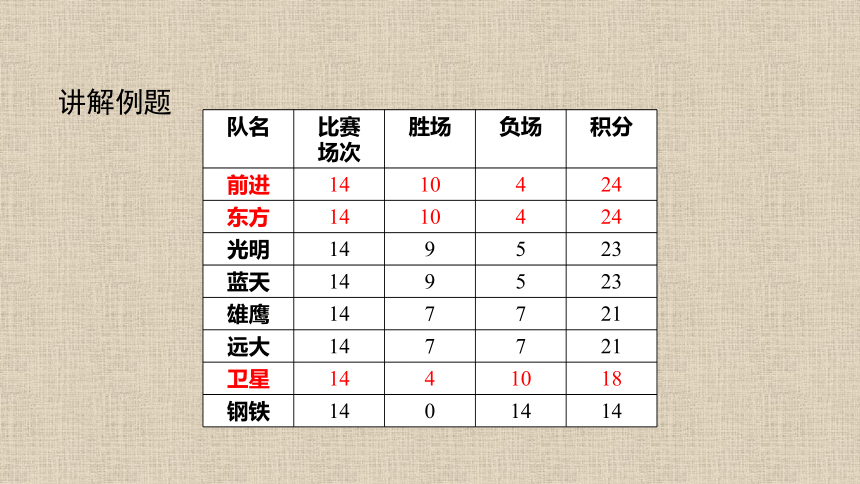
讲解例题
(2)总积分=胜场总积分+负场总积分;
分析:(1)胜场数+负场数=14;
想一想:哪些未知量是可以通过表格信息求出来的?
①钢铁队胜场总积分=0;
②钢铁队负场总积分=14=14×1;
③负一场积分=1.
分析:
队名 比赛场次 胜场 负场 积分
钢铁 14 0 14 14
讲解例题
队名 比赛 场次 胜场 负场 积分
前进 14 10 4 24
东方 14 10 4 24
光明 14 9 5 23
蓝天 14 9 5 23
雄鹰 14 7 7 21
远大 14 7 7 21
卫星 14 4 10 18
钢铁 14 0 14 14
①=1×4=4;
②前进队胜场总积分=20=2×10;
③胜一场积分=2.
分析:
队名 比赛场次 胜场 负场 积分
前进 14 10 4 24
未知量:
胜场总积分、负场总积分、胜一场积分、负一场积分
1
2
讲解例题
(3)胜场总积分=×胜场数
负场总积分=×负场数.
(2)总积分=胜场总积分+负场总积分;
分析:(1)胜场数+负场数=14;
胜场总积分、负场总积分、胜一场积分、负一场积分
1
2
分析:设若某队胜m场,则负(14m)场.
(14m)
2m
解:如果一个队胜m场,则负(14m)场.
胜场总积分为2m,负场总积分为14m,
总积分为
2m+(14m)=m+14.
讲解例题
解:设一个队胜x场,则负(14x)场.
如果这个队的胜场总积分等于负场总积分,则得方程
2x=14x.
由此得 x= .
检验,x= 是原方程的解但不符合实际意义.
答:没有哪个队的胜场总积分可以等于它的负场总积分.
14
3
14
3
想一想:某队的胜场总积分能等于它的负场总积分吗?
小结
1.这是一道探究篮球比赛积分的问题,由于它以表格的形式呈现,所以我们首先要通过观察表格,尽可能多地获取其中的信息;
队名 比赛 场次 胜场 负场 积分
前进 14 10 4 24
东方 14 10 4 24
光明 14 9 5 23
蓝天 14 9 5 23
雄鹰 14 7 7 21
远大 14 7 7 21
卫星 14 4 10 18
钢铁 14 0 14 14
小结
2.当遇到判断一个结论是否正确的问题时,我们可以先假设结论成立,然后依据这个假设列出方程,最后检验求出的解是否为所列方程的解,是否符合实际意义.
参赛者 答对题数 答错题数 得分
A 20 0 100
B 19 1 94
C 18 2 88
D 14 6 64
E 10 10 40
某电视台组织知识竞赛,共设20道选择题,各题分值相同,
每题必答.下表记录了5个参赛者的得分情况.
巩固练习
(1)参赛者F得76分,他答对了几道题?
(2)参赛者G说他得80分,你认为可能吗?为什么?
讲解练习
某电视台组织知识竞赛,共设20道选择题,各题分值
相同,每题必答.下表记录了5个参赛者的得分情况.
分析:(1)答对题数+答错题数=20;
参赛者 答对题数 答错题数 得分
A 20 0 100
B 19 1 94
C 18 2 88
D 14 6 64
E 10 10 40
讲解练习
(1)答对题数+答错题数=20;
(2)答对题得分+答错题得分=总得分;
分析:
参赛 者 答对 题数 答错 题数 得分
讲解练习
分析:(1)答对题数+答错题数=20;
(2)答对题得分+答错题得分=总得分;
(3)答对题得分=答对题数×
答错题得分=答错题数×.
参赛者 答对题数 答错题数 得分
A 20 0 100
B 19 1 94
C 18 2 88
D 14 6 64
E 10 10 40
讲解练习
想一想:哪些未知量是可以通过表格信息求出来的?
分析:(1)答对题数+答错题数=20;
(2)答对题得分+答错题得分=总得分;
(3)答对题得分=答对题数×
答错题得分=答错题数×.
讲解练习
分析:
① A答错题得分0;
② A答对题得分=100=20×5;
③对一题得分=5.
参赛者 答对题数 答错题数 得分
A 20 0 100
B 19 1 94
C 18 2 88
D 14 6 64
E 10 10 40
讲解练习
分析:
① E答对题得分=5×10=50;
② E答错题得分= 0= 1×10;
③错一题得分=.
参赛者 答对题数 答错题数 得分
A 20 0 100
B 19 1 94
C 18 2 88
D 14 6 64
E 10 10 40
未知量:
答对题得分 答错题得分 对一题得分 错一题得分
5
1
分析:(1)答对题数+答错题数=20;
(2)答对题得分+答错题得分=总得分;
(3)答对题得分=答对题数×
答错题得分=答错题数×.
分析:设某个人答对了n道题,则答错了(20n)道题.
答对题得分 答错题得分 对一题得分 错一题得分
5
1
5n
1×(20n)
(1)参赛者F得76分,他答对了几道题?
解:
设F答对了x道题,则答错了(20x)道题.
讲解练习
列出方程
5x+(1)×(20x)=76.
由此得 x=16.
(口头检验:x16是原方程的解且符合实际意义.)
答:他答对了16道题.
检验: 是原方程的解但不符合实际意义.
答:参赛者G不可能得80分.
(2)参赛者G说他得80分,你认为可能吗?为什么?
解:设G答对了m道题,则答错了(20m)道题.
假设G得80分,可列方程
5m+(1)×(20m)=80.
m=
50
3
m=
50
3
.
课堂小结
今天我们学习的内容是,利用一元一次方程的知识探究球赛积分问题.
在解决这类问题时
1.我们需要仔细观察题目中给出的表格,尽可能多地获取其中的信息,并由此表示或求出相关的未知量;
2.当遇到判断一个结论是否正确的问题时,我们可以先假设结论成立,然后依据这个假设列出方程,并求出它的解,最后检验求出的解是否为所列方程的解,是否符合实际意义.
实际问题与一元一次方程(四)
学习新知
例 某次篮球联赛积分榜
用式子表示总积分与胜、负场数之间的数量关系;
队名 比赛场次 胜场 负场 积分
前进 14 10 4 24
东方 14 10 4 24
光明 14 9 5 23
蓝天 14 9 5 23
雄鹰 14 7 7 21
远大 14 7 7 21
卫星 14 4 10 18
钢铁 14 0 14 14
讲解例题
(1)胜场数+负场数=14;
分析:
队名 比赛 场次 胜场 负场 积分
前进 14 10 4 24
东方 14 10 4 24
光明 14 9 5 23
蓝天 14 9 5 23
雄鹰 14 7 7 21
远大 14 7 7 21
卫星 14 4 10 18
钢铁 14 0 14 14
(1)胜场数+负场数=14;
分析:
队名 比赛 场次 胜场 负场 积分
前进 14 10 4 24
东方 14 10 4 24
光明 14 9 5 23
蓝天 14 9 5 23
雄鹰 14 7 7 21
远大 14 7 7 21
卫星 14 4 10 18
钢铁 14 0 14 14
(2)总积分=胜场总积分+负场总积分;
(1)胜场数+负场数=14;
分析:
(2)总积分=胜场总积分+负场总积分;
(3)胜场总积分=×胜场数
负场总积分=×负场数.
队名 比赛 场次 胜场 负场 积分
前进 14 10 4 24
东方 14 10 4 24
光明 14 9 5 23
蓝天 14 9 5 23
雄鹰 14 7 7 21
远大 14 7 7 21
卫星 14 4 10 18
钢铁 14 0 14 14
(3)胜场总积分=×胜场数
负场总积分=×负场数.
讲解例题
(2)总积分=胜场总积分+负场总积分;
分析:(1)胜场数+负场数=14;
想一想:哪些未知量是可以通过表格信息求出来的?
①钢铁队胜场总积分=0;
②钢铁队负场总积分=14=14×1;
③负一场积分=1.
分析:
队名 比赛场次 胜场 负场 积分
钢铁 14 0 14 14
讲解例题
队名 比赛 场次 胜场 负场 积分
前进 14 10 4 24
东方 14 10 4 24
光明 14 9 5 23
蓝天 14 9 5 23
雄鹰 14 7 7 21
远大 14 7 7 21
卫星 14 4 10 18
钢铁 14 0 14 14
①=1×4=4;
②前进队胜场总积分=20=2×10;
③胜一场积分=2.
分析:
队名 比赛场次 胜场 负场 积分
前进 14 10 4 24
未知量:
胜场总积分、负场总积分、胜一场积分、负一场积分
1
2
讲解例题
(3)胜场总积分=×胜场数
负场总积分=×负场数.
(2)总积分=胜场总积分+负场总积分;
分析:(1)胜场数+负场数=14;
胜场总积分、负场总积分、胜一场积分、负一场积分
1
2
分析:设若某队胜m场,则负(14m)场.
(14m)
2m
解:如果一个队胜m场,则负(14m)场.
胜场总积分为2m,负场总积分为14m,
总积分为
2m+(14m)=m+14.
讲解例题
解:设一个队胜x场,则负(14x)场.
如果这个队的胜场总积分等于负场总积分,则得方程
2x=14x.
由此得 x= .
检验,x= 是原方程的解但不符合实际意义.
答:没有哪个队的胜场总积分可以等于它的负场总积分.
14
3
14
3
想一想:某队的胜场总积分能等于它的负场总积分吗?
小结
1.这是一道探究篮球比赛积分的问题,由于它以表格的形式呈现,所以我们首先要通过观察表格,尽可能多地获取其中的信息;
队名 比赛 场次 胜场 负场 积分
前进 14 10 4 24
东方 14 10 4 24
光明 14 9 5 23
蓝天 14 9 5 23
雄鹰 14 7 7 21
远大 14 7 7 21
卫星 14 4 10 18
钢铁 14 0 14 14
小结
2.当遇到判断一个结论是否正确的问题时,我们可以先假设结论成立,然后依据这个假设列出方程,最后检验求出的解是否为所列方程的解,是否符合实际意义.
参赛者 答对题数 答错题数 得分
A 20 0 100
B 19 1 94
C 18 2 88
D 14 6 64
E 10 10 40
某电视台组织知识竞赛,共设20道选择题,各题分值相同,
每题必答.下表记录了5个参赛者的得分情况.
巩固练习
(1)参赛者F得76分,他答对了几道题?
(2)参赛者G说他得80分,你认为可能吗?为什么?
讲解练习
某电视台组织知识竞赛,共设20道选择题,各题分值
相同,每题必答.下表记录了5个参赛者的得分情况.
分析:(1)答对题数+答错题数=20;
参赛者 答对题数 答错题数 得分
A 20 0 100
B 19 1 94
C 18 2 88
D 14 6 64
E 10 10 40
讲解练习
(1)答对题数+答错题数=20;
(2)答对题得分+答错题得分=总得分;
分析:
参赛 者 答对 题数 答错 题数 得分
讲解练习
分析:(1)答对题数+答错题数=20;
(2)答对题得分+答错题得分=总得分;
(3)答对题得分=答对题数×
答错题得分=答错题数×.
参赛者 答对题数 答错题数 得分
A 20 0 100
B 19 1 94
C 18 2 88
D 14 6 64
E 10 10 40
讲解练习
想一想:哪些未知量是可以通过表格信息求出来的?
分析:(1)答对题数+答错题数=20;
(2)答对题得分+答错题得分=总得分;
(3)答对题得分=答对题数×
答错题得分=答错题数×.
讲解练习
分析:
① A答错题得分0;
② A答对题得分=100=20×5;
③对一题得分=5.
参赛者 答对题数 答错题数 得分
A 20 0 100
B 19 1 94
C 18 2 88
D 14 6 64
E 10 10 40
讲解练习
分析:
① E答对题得分=5×10=50;
② E答错题得分= 0= 1×10;
③错一题得分=.
参赛者 答对题数 答错题数 得分
A 20 0 100
B 19 1 94
C 18 2 88
D 14 6 64
E 10 10 40
未知量:
答对题得分 答错题得分 对一题得分 错一题得分
5
1
分析:(1)答对题数+答错题数=20;
(2)答对题得分+答错题得分=总得分;
(3)答对题得分=答对题数×
答错题得分=答错题数×.
分析:设某个人答对了n道题,则答错了(20n)道题.
答对题得分 答错题得分 对一题得分 错一题得分
5
1
5n
1×(20n)
(1)参赛者F得76分,他答对了几道题?
解:
设F答对了x道题,则答错了(20x)道题.
讲解练习
列出方程
5x+(1)×(20x)=76.
由此得 x=16.
(口头检验:x16是原方程的解且符合实际意义.)
答:他答对了16道题.
检验: 是原方程的解但不符合实际意义.
答:参赛者G不可能得80分.
(2)参赛者G说他得80分,你认为可能吗?为什么?
解:设G答对了m道题,则答错了(20m)道题.
假设G得80分,可列方程
5m+(1)×(20m)=80.
m=
50
3
m=
50
3
.
课堂小结
今天我们学习的内容是,利用一元一次方程的知识探究球赛积分问题.
在解决这类问题时
1.我们需要仔细观察题目中给出的表格,尽可能多地获取其中的信息,并由此表示或求出相关的未知量;
2.当遇到判断一个结论是否正确的问题时,我们可以先假设结论成立,然后依据这个假设列出方程,并求出它的解,最后检验求出的解是否为所列方程的解,是否符合实际意义.
