2020-2021学年高一下学期数学人教A版(2019)必修第二册8.3.1棱柱、棱锥、棱台的表面积和体积教学设计
文档属性
| 名称 | 2020-2021学年高一下学期数学人教A版(2019)必修第二册8.3.1棱柱、棱锥、棱台的表面积和体积教学设计 |

|
|
| 格式 | docx | ||
| 文件大小 | 620.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-12-27 00:00:00 | ||
图片预览


文档简介
8.3.1 棱柱、棱锥、棱台的表面积和体积
(人教A版普通高中教科书数学必修第二册第八章)
本节课选自《普通高中课程标准数学教科书-必修第二册》(人教A版)第八章《立体几何初步》,本节课主要学习棱柱、棱锥、棱台的表面积和体积的表面积、体积公式及其求法,还有简单组合体的体积的求解。
教材从分析简单几何体的侧面展开图得到了它们的表面积公式,体现了立体问题平面化的解决策略,这是本节课的灵魂,也是立体几何的灵魂,在立体几何中,要注意将立体问题转化为平面几何问题,在教学中应加以重视。
一、教学目标与数学学科素养
课程目标
1.通过对棱柱、棱锥、棱台的研究,掌握棱柱、棱锥、棱台的表面积和体积计算公式.
2.能运用棱柱、棱锥、棱台的表面积和体积公式进行计算和解决有关实际问题.
数学学科素养
1.数学抽象:棱柱、棱锥、棱台的体积公式;
2.数学运算:求多面体或多面体组合体的表面积和体积;
3.数学建模:数形结合,运用棱柱、棱锥、棱台的表面积和体积公式进行计算和解决有关实际问题.
二、教学重难点
1.教学重点:棱柱、棱锥、棱台的表面积与体积;
2.教学难点:求棱柱、棱锥、棱台有关的组合体的表面积与体积.
三、教学过程
1.表面积
1.1创设情境,引入课题
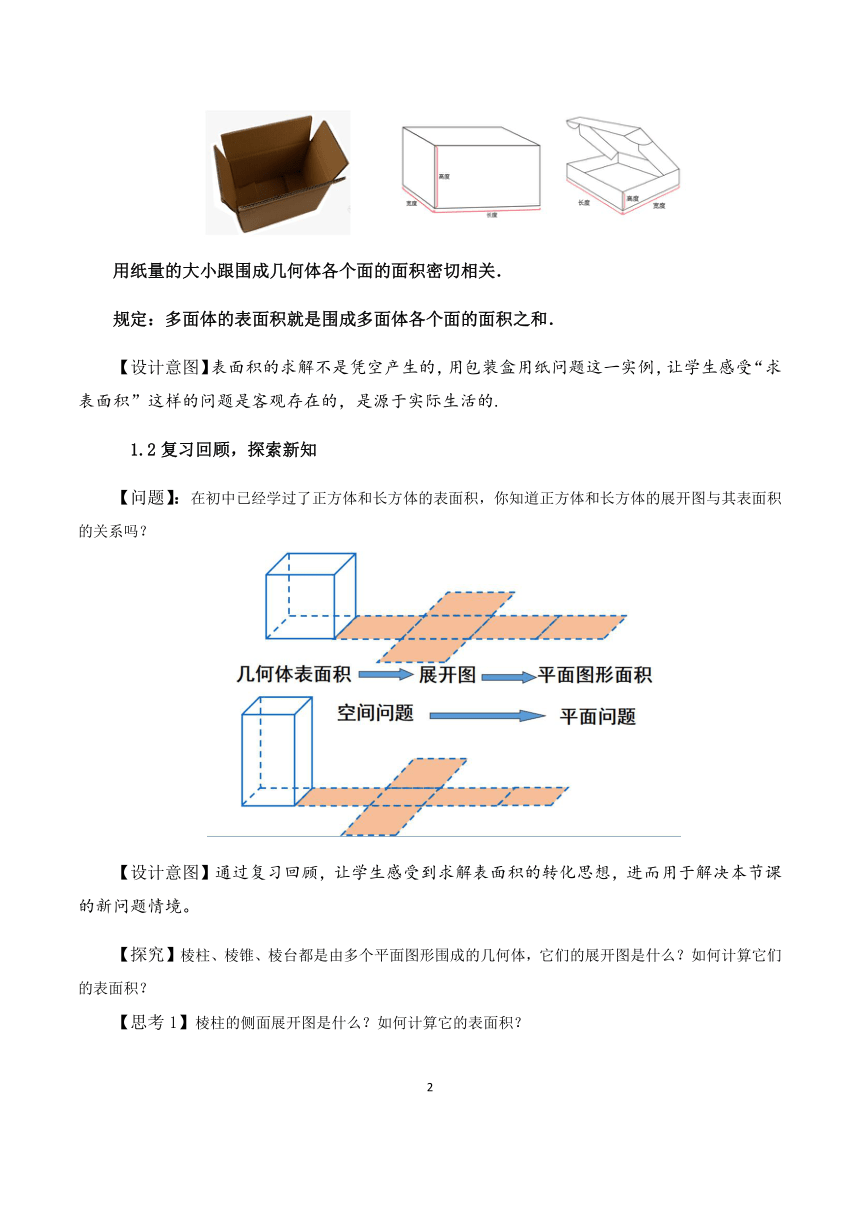
【实际情境】在生产生活中,会遇到包装盒用纸量的计算问题
用纸量的大小跟围成几何体各个面的面积密切相关.
规定:多面体的表面积就是围成多面体各个面的面积之和.
【设计意图】表面积的求解不是凭空产生的,用包装盒用纸问题这一实例,让学生感受“求表面积”这样的问题是客观存在的,是源于实际生活的.
1.2复习回顾,探索新知
【问题】:在初中已经学过了正方体和长方体的表面积,你知道正方体和长方体的展开图与其表面积的关系吗?
【设计意图】通过复习回顾,让学生感受到求解表面积的转化思想,进而用于解决本节课的新问题情境。
【探究】棱柱、棱锥、棱台都是由多个平面图形围成的几何体,它们的展开图是什么?如何计算它们的表面积?
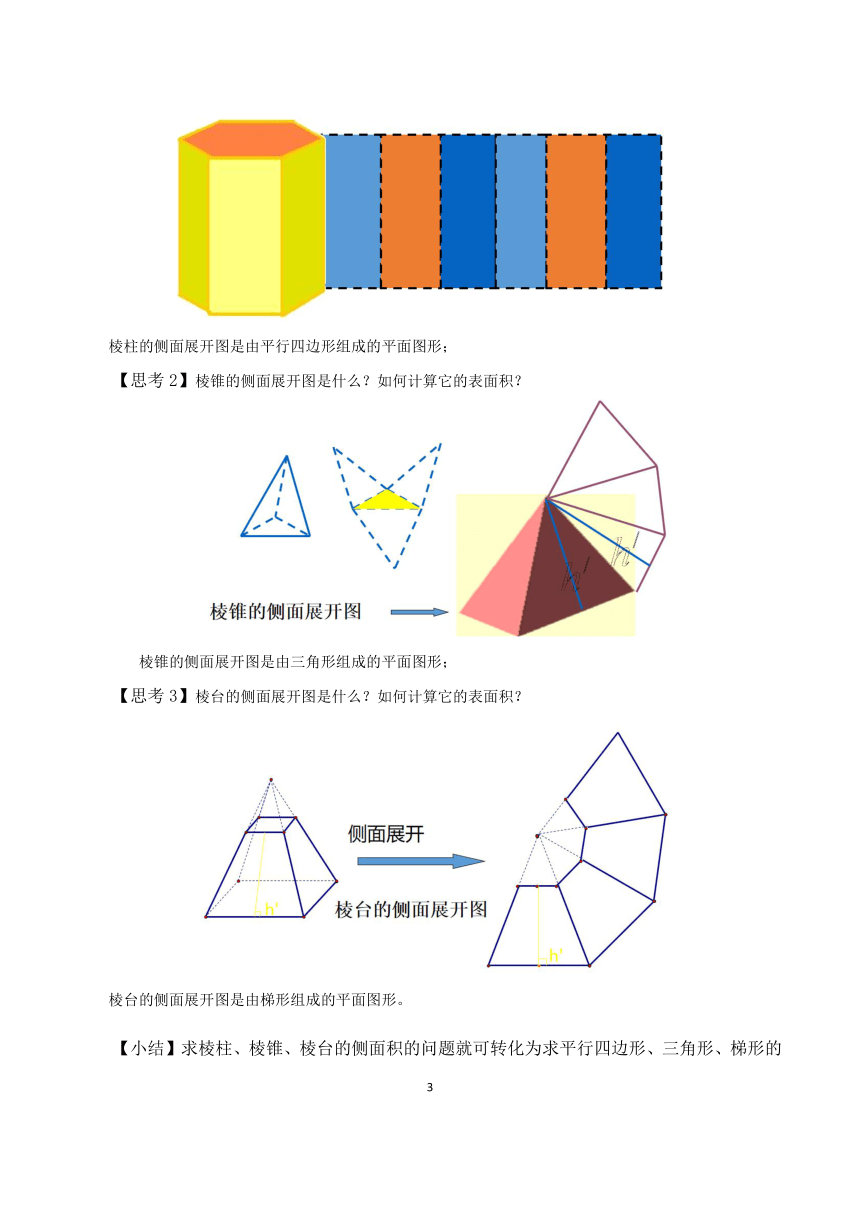
【思考1】棱柱的侧面展开图是什么?如何计算它的表面积?
棱柱的侧面展开图是由平行四边形组成的平面图形;
【思考2】棱锥的侧面展开图是什么?如何计算它的表面积?
棱锥的侧面展开图是由三角形组成的平面图形;
【思考3】棱台的侧面展开图是什么?如何计算它的表面积?
棱台的侧面展开图是由梯形组成的平面图形。
【小结】求棱柱、棱锥、棱台的侧面积的问题就可转化为求平行四边形、三角形、梯形的面积问题,而计算它们的表面积就是计算它的各个侧面面积和底面面积之和。
【设计意图】通过初中正方体,长方体表面积的求法,提炼出求解表面积的基本思想方法,并且在探究棱柱,棱锥,棱台的基础上,了解从空间问题到平面问题转化的思路,形成求解表面积问题的一般方法.
1.3典例分析,举一反三
例1 已知如图,四面体的棱长均为,求它的表面积.
【答案】
【解析】因为四面体S-ABC的四个面是全等的等边三角形,
所以四面体的表面积等于其中任何一个面面积的4倍.
不妨求△SBC的面积,过点S作SD⊥BC,交BC于点D,如图所示.
因为BC=SB=a,SD=,
所以S△SBC=BC·SD=a×a=a2.
故四面体S-ABC的表面积S=4×a2=a2.
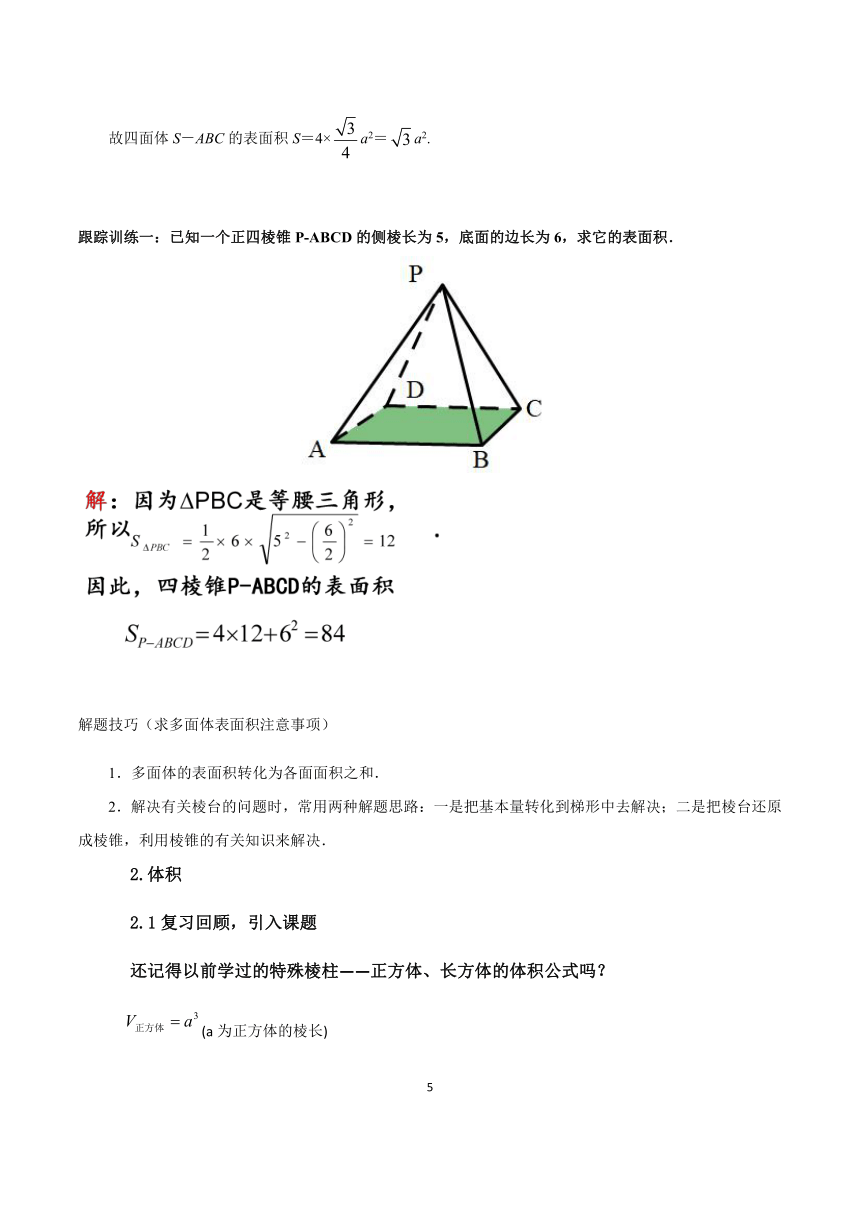
跟踪训练一:已知一个正四棱锥P-ABCD的侧棱长为5,底面的边长为6,求它的表面积.
解题技巧(求多面体表面积注意事项)
1.多面体的表面积转化为各面面积之和.
2.解决有关棱台的问题时,常用两种解题思路:一是把基本量转化到梯形中去解决;二是把棱台还原成棱锥,利用棱锥的有关知识来解决.
2.体积
2.1复习回顾,引入课题
还记得以前学过的特殊棱柱——正方体、长方体的体积公式吗?
(a为正方体的棱长)
(a、b、c为长方体的长、宽、高)
正方体、长方体的体积公式可以统一为:sh
2.2探索新知
【思考1】棱柱的体积公式是什么?如何计算它的体积?
一般地,如果棱柱的底面积是S,高是h,那么这个棱柱的体积V棱柱=sh
【思考2】棱锥的体积公式是什么?如何计算它的体积?
一个三棱柱可以分解成三个体积相等的三棱锥,如图所示:
如果一个棱柱和一个棱锥的底面积相等,高也相等,那么,棱柱的体积是棱锥的体积的3倍.
因此,一般地,如果棱锥的底面面积为S,高为h,那么该棱锥的体积
【思考3】棱台的体积公式是什么?如何计算它的体积?
【思考3】棱柱、棱锥、棱台的体积公式之间有什么关系?你能用棱柱、棱锥、棱台的结构特征来解释这种关系吗?
【设计意图】通过初中正方体,长方体体积公式,归纳出求解棱柱的体积公式。然后将棱柱分解,进而求出棱锥的体积公式。接着将棱台看成大棱锥截取一个小棱锥,通过一些相似知识的应用,进而得出棱台的体积公式。过程中让学生体会化归的基本思想方法,并且在探究棱柱,棱锥,棱台的基础上,感受求解体积问题的一般方法。最后再从形和数的角度让学生感受棱柱,棱锥,棱台的结构特征及其联系。
2.3典例分析,举一反三
例3 如图,一个漏斗的上面部分是一个长方体,下面部分是一个四棱锥,两部分的高都是0.5m,公共面是边长为1m的正方形,那么这个漏斗的容积是多少立方米(精确到)?
【答案】
【解析】由题意知长方体的体积,
棱锥的体积,
所以这个漏斗的容积
.
跟踪训练二:如图,已知ABCD-A1B1C1D1是棱长为a的正方体,E为AA1的中点,F为CC1上一点,求三棱锥A1-D1EF的体积.
解:(1)由V三棱锥A1-D1EF=V三棱锥F-A1D1E,
∵S△A1D1E=EA1·A1D1=a2,
又三棱锥F-A1D1E的高为CD=a,
∴V三棱锥F-A1D1E=×a×a2=a3,
∴V三棱锥A1-D1EF=a3.
解题技巧(求棱柱、棱锥、棱台体积的注意事项)
1.常见的求几何体体积的方法
①公式法:直接代入公式求解.②等积法:如四面体的任何一个面都可以作为底面,只需选用底面积和高都易求的形式即可.③分割法:将几何体分割成易求解的几部分,分别求体积.
2.求几何体体积时需注意的问题
柱、锥、台的体积的计算,一般要找出相应的底面和高,要充分利用截面、轴截面,求出所需要的量,最后代入公式计算.
归纳小结,提炼升华
1、求几何体的表面积
2、求几何体体积的常用方法
课外作业
四、教学反思
本节课的重点是掌握棱柱、棱锥、棱台的表面积和体积计算公式和应用,通过本节课的例题及练习,学生基本掌握.而本节课的难点可以通过三组体积公式对比,寻找其联系(棱台上底面和下底面面积一样时,图形变成棱柱,对应的公式,经推导也就变成棱柱的体积公式了; 棱台上底面无限缩小至点时,图形变成棱锥,对应的公式,经推导也就变成棱锥的体积公式了.)使学生对其更加理解.再有解决实际问题时可先抽象出几何图形,再利用相关公式解决.
2
(人教A版普通高中教科书数学必修第二册第八章)
本节课选自《普通高中课程标准数学教科书-必修第二册》(人教A版)第八章《立体几何初步》,本节课主要学习棱柱、棱锥、棱台的表面积和体积的表面积、体积公式及其求法,还有简单组合体的体积的求解。
教材从分析简单几何体的侧面展开图得到了它们的表面积公式,体现了立体问题平面化的解决策略,这是本节课的灵魂,也是立体几何的灵魂,在立体几何中,要注意将立体问题转化为平面几何问题,在教学中应加以重视。
一、教学目标与数学学科素养
课程目标
1.通过对棱柱、棱锥、棱台的研究,掌握棱柱、棱锥、棱台的表面积和体积计算公式.
2.能运用棱柱、棱锥、棱台的表面积和体积公式进行计算和解决有关实际问题.
数学学科素养
1.数学抽象:棱柱、棱锥、棱台的体积公式;
2.数学运算:求多面体或多面体组合体的表面积和体积;
3.数学建模:数形结合,运用棱柱、棱锥、棱台的表面积和体积公式进行计算和解决有关实际问题.
二、教学重难点
1.教学重点:棱柱、棱锥、棱台的表面积与体积;
2.教学难点:求棱柱、棱锥、棱台有关的组合体的表面积与体积.
三、教学过程
1.表面积
1.1创设情境,引入课题
【实际情境】在生产生活中,会遇到包装盒用纸量的计算问题
用纸量的大小跟围成几何体各个面的面积密切相关.
规定:多面体的表面积就是围成多面体各个面的面积之和.
【设计意图】表面积的求解不是凭空产生的,用包装盒用纸问题这一实例,让学生感受“求表面积”这样的问题是客观存在的,是源于实际生活的.
1.2复习回顾,探索新知
【问题】:在初中已经学过了正方体和长方体的表面积,你知道正方体和长方体的展开图与其表面积的关系吗?
【设计意图】通过复习回顾,让学生感受到求解表面积的转化思想,进而用于解决本节课的新问题情境。
【探究】棱柱、棱锥、棱台都是由多个平面图形围成的几何体,它们的展开图是什么?如何计算它们的表面积?
【思考1】棱柱的侧面展开图是什么?如何计算它的表面积?
棱柱的侧面展开图是由平行四边形组成的平面图形;
【思考2】棱锥的侧面展开图是什么?如何计算它的表面积?
棱锥的侧面展开图是由三角形组成的平面图形;
【思考3】棱台的侧面展开图是什么?如何计算它的表面积?
棱台的侧面展开图是由梯形组成的平面图形。
【小结】求棱柱、棱锥、棱台的侧面积的问题就可转化为求平行四边形、三角形、梯形的面积问题,而计算它们的表面积就是计算它的各个侧面面积和底面面积之和。
【设计意图】通过初中正方体,长方体表面积的求法,提炼出求解表面积的基本思想方法,并且在探究棱柱,棱锥,棱台的基础上,了解从空间问题到平面问题转化的思路,形成求解表面积问题的一般方法.
1.3典例分析,举一反三
例1 已知如图,四面体的棱长均为,求它的表面积.
【答案】
【解析】因为四面体S-ABC的四个面是全等的等边三角形,
所以四面体的表面积等于其中任何一个面面积的4倍.
不妨求△SBC的面积,过点S作SD⊥BC,交BC于点D,如图所示.
因为BC=SB=a,SD=,
所以S△SBC=BC·SD=a×a=a2.
故四面体S-ABC的表面积S=4×a2=a2.
跟踪训练一:已知一个正四棱锥P-ABCD的侧棱长为5,底面的边长为6,求它的表面积.
解题技巧(求多面体表面积注意事项)
1.多面体的表面积转化为各面面积之和.
2.解决有关棱台的问题时,常用两种解题思路:一是把基本量转化到梯形中去解决;二是把棱台还原成棱锥,利用棱锥的有关知识来解决.
2.体积
2.1复习回顾,引入课题
还记得以前学过的特殊棱柱——正方体、长方体的体积公式吗?
(a为正方体的棱长)
(a、b、c为长方体的长、宽、高)
正方体、长方体的体积公式可以统一为:sh
2.2探索新知
【思考1】棱柱的体积公式是什么?如何计算它的体积?
一般地,如果棱柱的底面积是S,高是h,那么这个棱柱的体积V棱柱=sh
【思考2】棱锥的体积公式是什么?如何计算它的体积?
一个三棱柱可以分解成三个体积相等的三棱锥,如图所示:
如果一个棱柱和一个棱锥的底面积相等,高也相等,那么,棱柱的体积是棱锥的体积的3倍.
因此,一般地,如果棱锥的底面面积为S,高为h,那么该棱锥的体积
【思考3】棱台的体积公式是什么?如何计算它的体积?
【思考3】棱柱、棱锥、棱台的体积公式之间有什么关系?你能用棱柱、棱锥、棱台的结构特征来解释这种关系吗?
【设计意图】通过初中正方体,长方体体积公式,归纳出求解棱柱的体积公式。然后将棱柱分解,进而求出棱锥的体积公式。接着将棱台看成大棱锥截取一个小棱锥,通过一些相似知识的应用,进而得出棱台的体积公式。过程中让学生体会化归的基本思想方法,并且在探究棱柱,棱锥,棱台的基础上,感受求解体积问题的一般方法。最后再从形和数的角度让学生感受棱柱,棱锥,棱台的结构特征及其联系。
2.3典例分析,举一反三
例3 如图,一个漏斗的上面部分是一个长方体,下面部分是一个四棱锥,两部分的高都是0.5m,公共面是边长为1m的正方形,那么这个漏斗的容积是多少立方米(精确到)?
【答案】
【解析】由题意知长方体的体积,
棱锥的体积,
所以这个漏斗的容积
.
跟踪训练二:如图,已知ABCD-A1B1C1D1是棱长为a的正方体,E为AA1的中点,F为CC1上一点,求三棱锥A1-D1EF的体积.
解:(1)由V三棱锥A1-D1EF=V三棱锥F-A1D1E,
∵S△A1D1E=EA1·A1D1=a2,
又三棱锥F-A1D1E的高为CD=a,
∴V三棱锥F-A1D1E=×a×a2=a3,
∴V三棱锥A1-D1EF=a3.
解题技巧(求棱柱、棱锥、棱台体积的注意事项)
1.常见的求几何体体积的方法
①公式法:直接代入公式求解.②等积法:如四面体的任何一个面都可以作为底面,只需选用底面积和高都易求的形式即可.③分割法:将几何体分割成易求解的几部分,分别求体积.
2.求几何体体积时需注意的问题
柱、锥、台的体积的计算,一般要找出相应的底面和高,要充分利用截面、轴截面,求出所需要的量,最后代入公式计算.
归纳小结,提炼升华
1、求几何体的表面积
2、求几何体体积的常用方法
课外作业
四、教学反思
本节课的重点是掌握棱柱、棱锥、棱台的表面积和体积计算公式和应用,通过本节课的例题及练习,学生基本掌握.而本节课的难点可以通过三组体积公式对比,寻找其联系(棱台上底面和下底面面积一样时,图形变成棱柱,对应的公式,经推导也就变成棱柱的体积公式了; 棱台上底面无限缩小至点时,图形变成棱锥,对应的公式,经推导也就变成棱锥的体积公式了.)使学生对其更加理解.再有解决实际问题时可先抽象出几何图形,再利用相关公式解决.
2
同课章节目录
- 第六章 平面向量及其应用
- 6.1 平面向量的概念
- 6.2 平面向量的运算
- 6.3 平面向量基本定理及坐标表示
- 6.4 平面向量的应用
- 第七章 复数
- 7.1 复数的概念
- 7.2 复数的四则运算
- 7.3 * 复数的三角表示
- 第八章 立体几何初步
- 8.1 基本立体图形
- 8.2 立体图形的直观图
- 8.3 简单几何体的表面积与体积
- 8.4 空间点、直线、平面之间的位置关系
- 8.5 空间直线、平面的平行
- 8.6 空间直线、平面的垂直
- 第九章 统计
- 9.1 随机抽样
- 9.2 用样本估计总体
- 9.3 统计分析案例 公司员工
- 第十章 概率
- 10.1 随机事件与概率
- 10.2 事件的相互独立性
- 10.3 频率与概率
