2021—2022学年华东师大版八年级数学下册17.5.1一次函数与二元一次方程(组) 同步练习(word版、含答案)
文档属性
| 名称 | 2021—2022学年华东师大版八年级数学下册17.5.1一次函数与二元一次方程(组) 同步练习(word版、含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 140.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-12-28 14:39:07 | ||
图片预览



文档简介
17.5 第1课时 一次函数与二元一次方程(组)
一、选择题
1.如图1,在平面直角坐标系中,一次函数y=kx+b和y=mx+n的图象相交于点(2,-1),则关于x,y的方程组的解是 ( )
图1
A. B.
C. D.
2.已知一次函数y=ax+2的图象与x轴的交点坐标为(3,0),则关于x的一元一次方程ax+2=0的解为 ( )
A.x=3 B.x=0 C.x=2 D.x=a
3.下面的四条直线中,直线上每个点的坐标都是二元一次方程2x-y=2的解的是 ( )
图2
4.直线y=x+1和y=2x+a的交点在第一象限,则a的取值可以是 ( )
A.-1 B.0 C.1 D.2
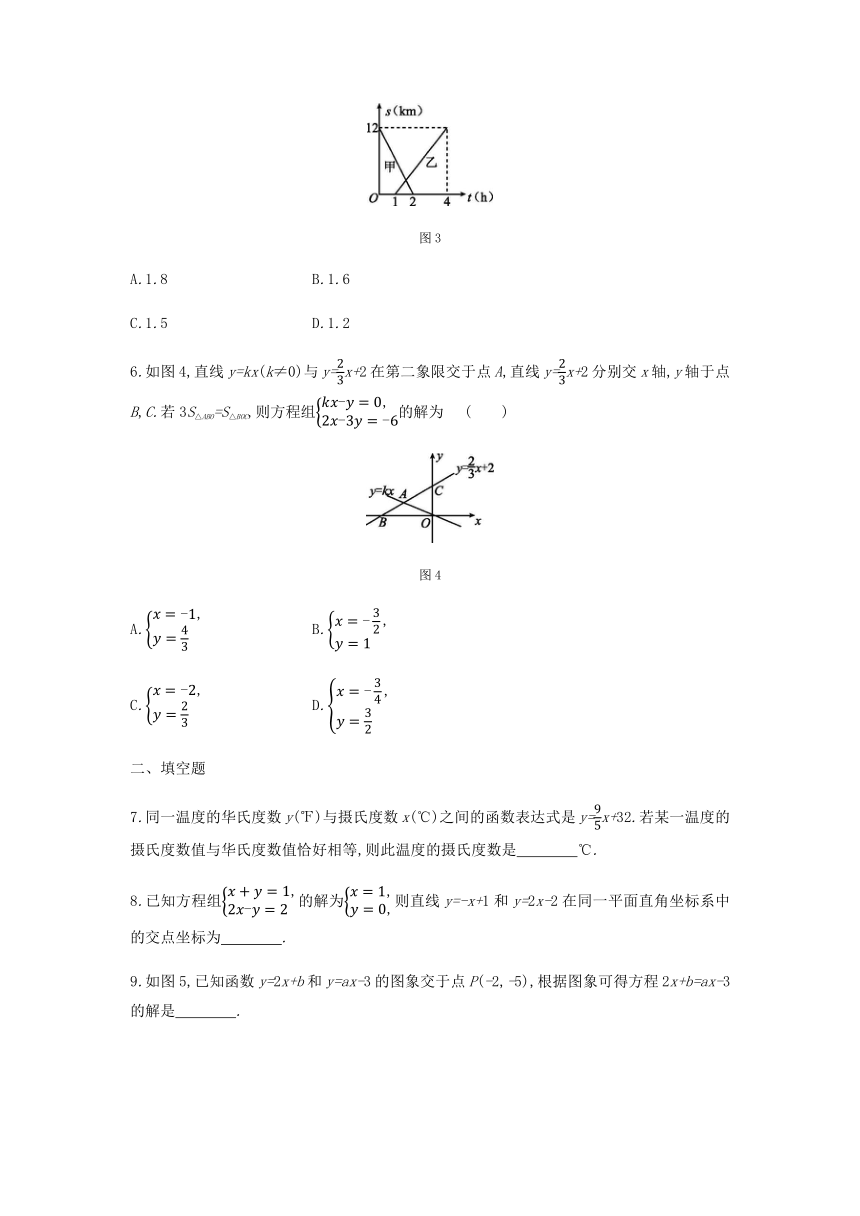
5.已知A,B两地相距12 km,甲、乙两人沿同一条公路分别从A,B两地出发相向而行,甲、乙两人离B地的距离s(km)与时间t(h)的函数关系图象如图3所示,则在甲出发
h后两人相遇 ( )
图3
A.1.8 B.1.6
C.1.5 D.1.2
6.如图4,直线y=kx(k≠0)与y=x+2在第二象限交于点A,直线y=x+2分别交x轴,y轴于点B,C.若3S△ABO=S△BOC,则方程组的解为 ( )
图4
A. B.
C. D.
二、填空题
7.同一温度的华氏度数y(℉)与摄氏度数x(℃)之间的函数表达式是y=x+32.若某一温度的摄氏度数值与华氏度数值恰好相等,则此温度的摄氏度数是 ℃.
8.已知方程组的解为则直线y=-x+1和y=2x-2在同一平面直角坐标系中的交点坐标为 .
9.如图5,已知函数y=2x+b和y=ax-3的图象交于点P(-2,-5),根据图象可得方程2x+b=ax-3的解是 .
图5
10.若直线y=x+b和直线y=-x+a的交点坐标为(m,8),则a+b= .
11.在平面直角坐标系中,一次函数y=k1x+b1与y=k2x+b2的图象如图6所示,则关于x,y的方程组的解是 .
图6
三、解答题
12.利用一次函数图象,求二元一次方程组的解.
13.(1)请在如图7所示的平面直角坐标系中画出一次函数y1=x+1和y2=-x+3的图象;
(2)根据图象直接写出方程组的解为 ;
(3)利用图象直接写出当x在什么范围内时,y1>y2>0.
图7
14.如图8,直线y1=2x-2与y轴交于点A,直线y2=-2x+6与y轴交于点B,两者相交于点C.
(1)方程组的解是 ;
(2)当y1>0与y2>0同时成立时,x的取值范围为 ;
(3)求△ABC的面积;
(4)在直线y1=2x-2上存在异于点C的另一点P,使得△ABC与△ABP的面积相等,请求出点P的坐标.
图8
答案
1.B
2.A
3.B
4.D
5.B
6.C
7.-40
8.(1,0)
9.x=-2
10.16
11.
12.解:将原方程组变形,得
在同一平面直角坐标系中,画出函数y=2x+4与y=-x-2的图象,如图所示:
观察图象得出直线y=2x+4与y=-x-2的交点坐标为(-2,0),即二元一次方程组的解为
13.[解析] (1)分别令x=0求出y的值,令y=0求出x的值,再分别描出此两点,画出函数图象即可.
(2)由(1)中两函数图象可知,其交点坐标为(1,2),
则方程组的解为
(3)根据y1在y2的上方并且都在x轴上方时x的取值范围即可解答.
解:(1)如图所示.
(2)
(3)由(1)中两函数图象可知,当1y2>0.
14.解:(1) (2)1(3)由(1)知C(2,2).
令x=0,则y1=-2,y2=6,
∴A(0,-2),B(0,6),
∴AB=8,∴S△ABC=×8×2=8.
(4)令P(x0,2x0-2).
∵△ABC与△ABP的面积相等,
∴S△ABP=×8×|x0|=8,
∴x0=±2.
∵点P异于点C,
∴x0=-2,2x0-2=-6,
∴点P的坐标为(-2,-6).
一、选择题
1.如图1,在平面直角坐标系中,一次函数y=kx+b和y=mx+n的图象相交于点(2,-1),则关于x,y的方程组的解是 ( )
图1
A. B.
C. D.
2.已知一次函数y=ax+2的图象与x轴的交点坐标为(3,0),则关于x的一元一次方程ax+2=0的解为 ( )
A.x=3 B.x=0 C.x=2 D.x=a
3.下面的四条直线中,直线上每个点的坐标都是二元一次方程2x-y=2的解的是 ( )
图2
4.直线y=x+1和y=2x+a的交点在第一象限,则a的取值可以是 ( )
A.-1 B.0 C.1 D.2
5.已知A,B两地相距12 km,甲、乙两人沿同一条公路分别从A,B两地出发相向而行,甲、乙两人离B地的距离s(km)与时间t(h)的函数关系图象如图3所示,则在甲出发
h后两人相遇 ( )
图3
A.1.8 B.1.6
C.1.5 D.1.2
6.如图4,直线y=kx(k≠0)与y=x+2在第二象限交于点A,直线y=x+2分别交x轴,y轴于点B,C.若3S△ABO=S△BOC,则方程组的解为 ( )
图4
A. B.
C. D.
二、填空题
7.同一温度的华氏度数y(℉)与摄氏度数x(℃)之间的函数表达式是y=x+32.若某一温度的摄氏度数值与华氏度数值恰好相等,则此温度的摄氏度数是 ℃.
8.已知方程组的解为则直线y=-x+1和y=2x-2在同一平面直角坐标系中的交点坐标为 .
9.如图5,已知函数y=2x+b和y=ax-3的图象交于点P(-2,-5),根据图象可得方程2x+b=ax-3的解是 .
图5
10.若直线y=x+b和直线y=-x+a的交点坐标为(m,8),则a+b= .
11.在平面直角坐标系中,一次函数y=k1x+b1与y=k2x+b2的图象如图6所示,则关于x,y的方程组的解是 .
图6
三、解答题
12.利用一次函数图象,求二元一次方程组的解.
13.(1)请在如图7所示的平面直角坐标系中画出一次函数y1=x+1和y2=-x+3的图象;
(2)根据图象直接写出方程组的解为 ;
(3)利用图象直接写出当x在什么范围内时,y1>y2>0.
图7
14.如图8,直线y1=2x-2与y轴交于点A,直线y2=-2x+6与y轴交于点B,两者相交于点C.
(1)方程组的解是 ;
(2)当y1>0与y2>0同时成立时,x的取值范围为 ;
(3)求△ABC的面积;
(4)在直线y1=2x-2上存在异于点C的另一点P,使得△ABC与△ABP的面积相等,请求出点P的坐标.
图8
答案
1.B
2.A
3.B
4.D
5.B
6.C
7.-40
8.(1,0)
9.x=-2
10.16
11.
12.解:将原方程组变形,得
在同一平面直角坐标系中,画出函数y=2x+4与y=-x-2的图象,如图所示:
观察图象得出直线y=2x+4与y=-x-2的交点坐标为(-2,0),即二元一次方程组的解为
13.[解析] (1)分别令x=0求出y的值,令y=0求出x的值,再分别描出此两点,画出函数图象即可.
(2)由(1)中两函数图象可知,其交点坐标为(1,2),
则方程组的解为
(3)根据y1在y2的上方并且都在x轴上方时x的取值范围即可解答.
解:(1)如图所示.
(2)
(3)由(1)中两函数图象可知,当1
14.解:(1) (2)1
令x=0,则y1=-2,y2=6,
∴A(0,-2),B(0,6),
∴AB=8,∴S△ABC=×8×2=8.
(4)令P(x0,2x0-2).
∵△ABC与△ABP的面积相等,
∴S△ABP=×8×|x0|=8,
∴x0=±2.
∵点P异于点C,
∴x0=-2,2x0-2=-6,
∴点P的坐标为(-2,-6).
