新人教版八年级下册19.2正方形变换说课
文档属性
| 名称 | 新人教版八年级下册19.2正方形变换说课 |

|
|
| 格式 | zip | ||
| 文件大小 | 15.4MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2012-10-30 00:00:00 | ||
图片预览











文档简介
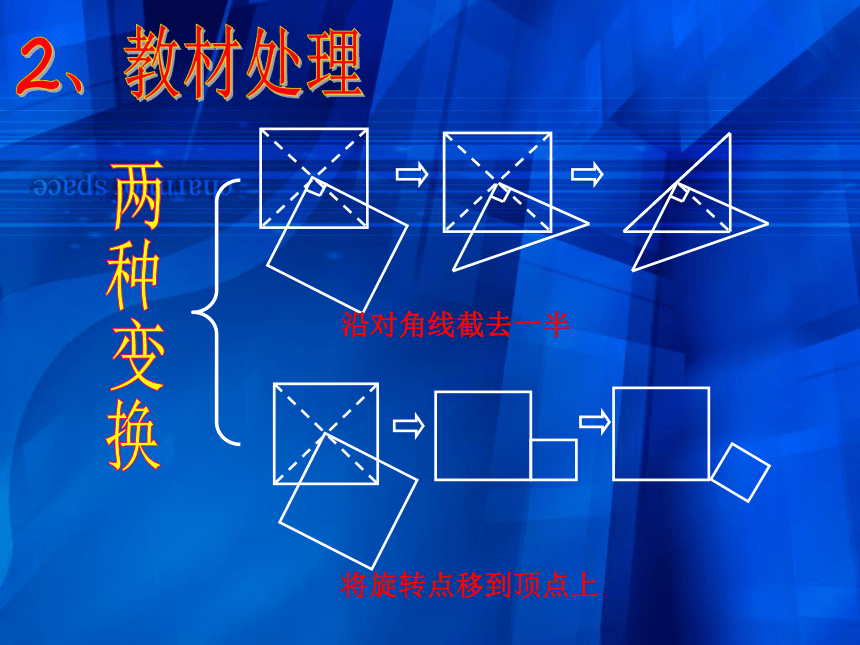
课件42张PPT。正方形变换专题学习一、教材分析二、学情分析三、教法学法与教学手段四、教学程序设计五、教学设计说明1、教材的地位与作用 既是三角形全等和正方形的性质等相关知识的综合应用,又为后继学习图形变换做好铺垫。 2、教材处理2、教材处理两种变换3、教学目标 掌握两个正方形旋转问题的两种基本解法,学会灵活应用。培养学生的识图能力,分析能力,推理能力。 3、教学目标 经历对两个正方形变换的探究,让学生体会知识的发生、发展、形成的过程,在变化当中找不变的量,构建全等三角形,从而掌握解决图形变换的基本方法。3、教学目标 通过合作交流,增强团队意识;利用图形的不断变换来激发学生的学习兴趣和探究欲望,从而体验成功的快乐。3、教学目标重点:利用正方形的性质寻找不变量及构造全等三角形。
难点:从复杂图形中找到基本图形及合理添辅助线。 4、教学重点难点一、教材分析二、学情分析三、教法学法与教学手段四、教学程序设计五、教学设计说明 采用研究体验式教学方法。
主动探究,合作交流教 法 学 法三、教法学法与教学手段多媒体
材料单 教 学 手 段三、教法学法与教学手段四、教学程序设计环节一:欣赏 导课
环节二:探究 说理
环节三:变式 开放
环节四:感悟 收获
环节五:拓展 延伸
⊥环节一:欣赏 导课
⊥以学生生活世界为切入点环节一:欣赏 导课
⊥环节二:探究 说理
教材中的基本图形: 正方形ABCD的对角线相交于点O,以点O为一个顶点作正方A′B′C′O,且2OA′>AC,说明正方形A′B′C′O绕点O无论怎样转动,两个正方形重叠部分的面积等于正方形ABCD 面积的四分之一。探究: 如图所示,正方形ABCD的对角线相交于点O,以点O为一个顶点作正方A′B′C′O,且2OA′>AC,说明正方形A′B′C′O绕点O无论怎样转动,两个正方形重叠部分的面积等于正方形ABCD 面积的四分之一。探究:解法1:利用两正方形边、对角线及其夹角,找不变的量,直接构造全等 三角形。MN解法2:正方形的对角线又是角平分线,添加垂线构造全等三角形。43构造全等两正方形边、对角线及夹角找到两个基本三角形作出两个直角三角形正方形对角线又是角平分线我来总结方法(找不变量构全等)⊥环节二:探究 说理
以学生合作学习为关键点环节三:变式 开放
一、探究图形变换变式训练: 一幅三角板,将含30度角的三角板直角顶点放在斜边AC的中点D处,然后绕点D旋转,两直角边分别交AB、CB于M、N两点。线段DM与DN之间有怎样的数量关系?并结合图2或图3加以证明;DM=DNDM=DNDM=DN44二、探究题型变换图1 图2图3BG =DE BG=DE BG=DE △BGC≌ △DEC小正方形一个顶点绕大正方形的一个顶点旋转,如下三图,试探究BG和DE之间的数量关系。变式训练:⊥环节三:变式 开放
以学生发散思维为立足点我来谈收获……环节四:感悟 收获
图形变换并不难,关键常在辅助线;条件分析找全等,首图常把方法现;等腰直角斜中点,可向两边作垂线; 图三如若不成立,加改减来试试看; 三图方法趋一致,变化当中找不变。点点感悟在心头以学生可持续发展为落脚点环节五:拓展 延伸
以学生应用意识为实践点正方形变换两个正方形旋转问题证明 方法总结 学生板演板书设计:以学生的发展为本让学生在创设的情境中愉快的学习; 在经历体验中感悟学习; 在合作交流中深化学习; 在问题解决中理解学习; 在实践活动中应用学习; 使学生真正成为数学学习的主人。五、教学设计说明作业训练:图形变式难不难,关键常在辅助线;条件分析找全等,首图常把方法现 ;等腰直角斜中点,可向两边作垂线; 图三如若不成立,加改减来试试看; 三图方法趋一致,变化当中找不变;数学需靠勤钻研,细心思维能闯关。反思小结,以学生的可持续发展为落脚点第四板块:
掌握两个正方形旋转问题的两种基本解法,学会灵活应用。培养学生的识图能力,分析能力,推理能力。 2、教学目标
难点:从复杂图形中找到基本图形及合理添辅助线。 4、教学重点难点一、教材分析二、学情分析三、教法学法与教学手段四、教学程序设计五、教学设计说明 采用研究体验式教学方法。
主动探究,合作交流教 法 学 法三、教法学法与教学手段多媒体
材料单 教 学 手 段三、教法学法与教学手段四、教学程序设计环节一:欣赏 导课
环节二:探究 说理
环节三:变式 开放
环节四:感悟 收获
环节五:拓展 延伸
⊥环节一:欣赏 导课
⊥以学生生活世界为切入点环节一:欣赏 导课
⊥环节二:探究 说理
教材中的基本图形: 正方形ABCD的对角线相交于点O,以点O为一个顶点作正方A′B′C′O,且2OA′>AC,说明正方形A′B′C′O绕点O无论怎样转动,两个正方形重叠部分的面积等于正方形ABCD 面积的四分之一。探究: 如图所示,正方形ABCD的对角线相交于点O,以点O为一个顶点作正方A′B′C′O,且2OA′>AC,说明正方形A′B′C′O绕点O无论怎样转动,两个正方形重叠部分的面积等于正方形ABCD 面积的四分之一。探究:解法1:利用两正方形边、对角线及其夹角,找不变的量,直接构造全等 三角形。MN解法2:正方形的对角线又是角平分线,添加垂线构造全等三角形。43构造全等两正方形边、对角线及夹角找到两个基本三角形作出两个直角三角形正方形对角线又是角平分线我来总结方法(找不变量构全等)⊥环节二:探究 说理
以学生合作学习为关键点环节三:变式 开放
一、探究图形变换变式训练: 一幅三角板,将含30度角的三角板直角顶点放在斜边AC的中点D处,然后绕点D旋转,两直角边分别交AB、CB于M、N两点。线段DM与DN之间有怎样的数量关系?并结合图2或图3加以证明;DM=DNDM=DNDM=DN44二、探究题型变换图1 图2图3BG =DE BG=DE BG=DE △BGC≌ △DEC小正方形一个顶点绕大正方形的一个顶点旋转,如下三图,试探究BG和DE之间的数量关系。变式训练:⊥环节三:变式 开放
以学生发散思维为立足点我来谈收获……环节四:感悟 收获
图形变换并不难,关键常在辅助线;条件分析找全等,首图常把方法现;等腰直角斜中点,可向两边作垂线; 图三如若不成立,加改减来试试看; 三图方法趋一致,变化当中找不变。点点感悟在心头以学生可持续发展为落脚点环节五:拓展 延伸
以学生应用意识为实践点正方形变换两个正方形旋转问题证明 方法总结 学生板演板书设计:以学生的发展为本让学生在创设的情境中愉快的学习; 在经历体验中感悟学习; 在合作交流中深化学习; 在问题解决中理解学习; 在实践活动中应用学习; 使学生真正成为数学学习的主人。五、教学设计说明作业训练:图形变式难不难,关键常在辅助线;条件分析找全等,首图常把方法现 ;等腰直角斜中点,可向两边作垂线; 图三如若不成立,加改减来试试看; 三图方法趋一致,变化当中找不变;数学需靠勤钻研,细心思维能闯关。反思小结,以学生的可持续发展为落脚点第四板块:
掌握两个正方形旋转问题的两种基本解法,学会灵活应用。培养学生的识图能力,分析能力,推理能力。 2、教学目标
