山东省临沂市滨河区高级中学校2022届高三上学期12月阶段性检测数学试卷(PDF版含答案)
文档属性
| 名称 | 山东省临沂市滨河区高级中学校2022届高三上学期12月阶段性检测数学试卷(PDF版含答案) |  | |
| 格式 | |||
| 文件大小 | 535.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-12-27 11:26:09 | ||
图片预览


文档简介
2021-2022学年度高三阶段性检测
数学
本试卷共 6页,共 150分,考试时间 120分钟
注意事项:
1.答题前,考生先将自己的姓名、考生号、座号填写在相应位置,认真核对条形码上的
姓名、考生号和座号,并将条形码粘贴在指定位置上。
2.选择题答案必须使用 2B铅笔(按填涂样例)正确填涂,非选择题答案必须使用 0. 5
毫米黑色签字笔书写,字体工整、笔迹清楚。
3.请按照题号在各题目的答题区域内作答,超出答题区域书写的答案无效;在草稿纸、
试题卷上答题无效。保持卡面清洁,不折叠、不破损。
第 I 卷(选择题)
一、单项选择题(本题共 8小题,每小题 5分,共 40分. 在每小题给出的四个选项中,
只有一项是符合题目要求.)
1.已知集合M {x | y ln(x 1)} . N y | y ex ,则M N ( )
A. ( 1,0) B. ( 1, ) C. (0, ) D. R
1
2.如图,若向量OZ对应的复数为 z,且 z 5,则 ( )z
1 2 i 1 2 i 1 2 1 2A. B. C. i D. i
5 5 5 5 5 5 5 5
2 13. (x 2 2)
3
展开式中的常数项为
x
A. 20 B. 20 C. 12 D. 8
4.函数 y cos x ln | x |的图象可能是( )
A. B.
C. D.
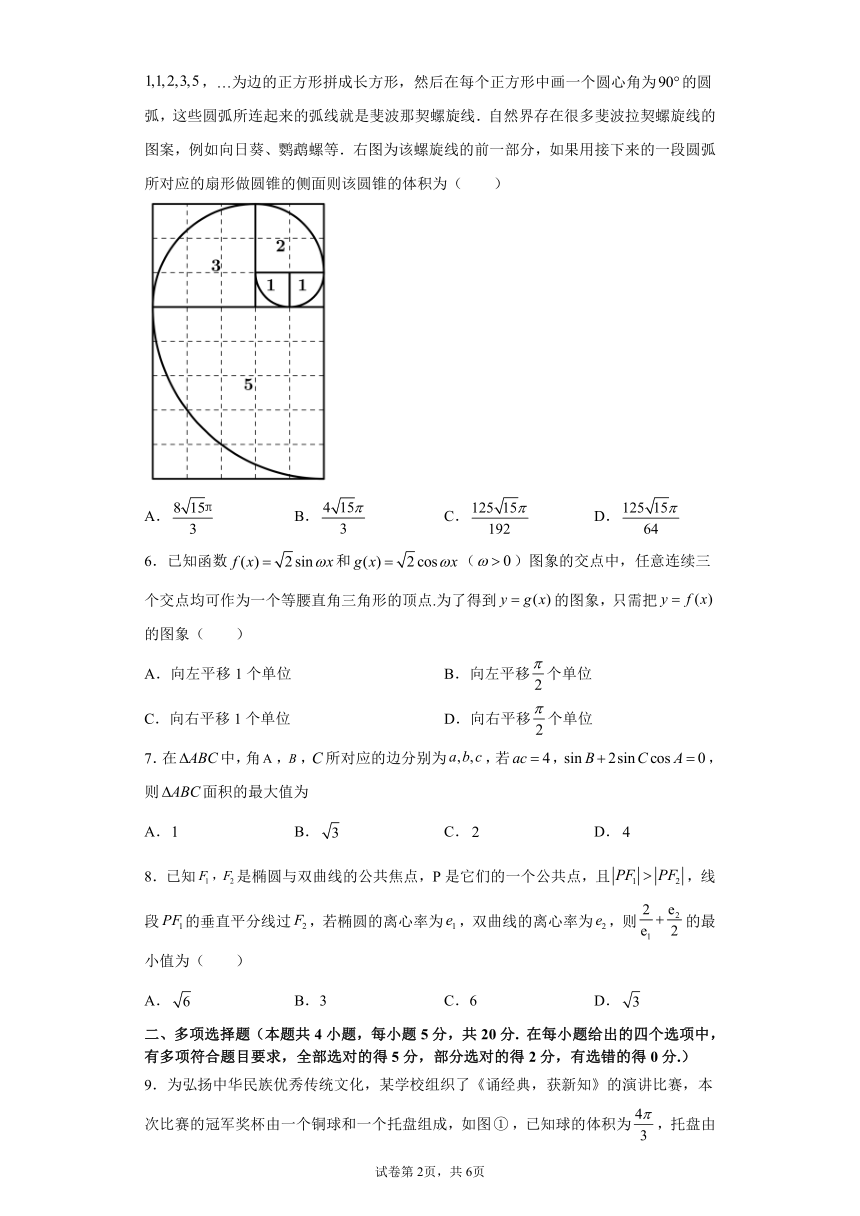
5.斐波那契螺旋线被誉为自然界最完美的“黄金螺旋”,它的画法是:以斐波那契数:
试卷第 1页,共 6页
1,1,2,3,5,…为边的正方形拼成长方形,然后在每个正方形中画一个圆心角为90 的圆
弧,这些圆弧所连起来的弧线就是斐波那契螺旋线.自然界存在很多斐波拉契螺旋线的
图案,例如向日葵、鹦鹉螺等.右图为该螺旋线的前一部分,如果用接下来的一段圆弧
所对应的扇形做圆锥的侧面则该圆锥的体积为( )
A 8 15π. B 4 15 C 125 15 D 125 15 . . .
3 3 192 64
6.已知函数 f (x) 2 sin x和 g(x) 2 cos x( 0)图象的交点中,任意连续三
个交点均可作为一个等腰直角三角形的顶点.为了得到 y g(x)的图象,只需把 y f (x)
的图象( )
A.向左平移 1个单位 B.向左平移 个单位
2
C.向右平移 1个单位 D.向右平移 个单位
2
7.在 ABC中,角A,B,C所对应的边分别为 a,b,c,若 ac 4,sin B 2sinC cos A 0,
则 ABC面积的最大值为
A.1 B. 3 C.2 D. 4
8.已知 F1,F2是椭圆与双曲线的公共焦点,P是它们的一个公共点,且 PF1 PF2 ,线
2 e2
段 PF1的垂直平分线过 F2,若椭圆的离心率为 e1,双曲线的离心率为 e2,则 e 的最1 2
小值为( )
A. 6 B.3 C.6 D. 3
二、多项选择题(本题共 4小题,每小题 5分,共 20分. 在每小题给出的四个选项中,
有多项符合题目要求,全部选对的得 5分,部分选对的得 2分,有选错的得 0分.)
9.为弘扬中华民族优秀传统文化,某学校组织了《诵经典,获新知》的演讲比赛,本
4
次比赛的冠军奖杯由一个铜球和一个托盘组成,如图①,已知球的体积为 ,托盘由
3
试卷第 2页,共 6页
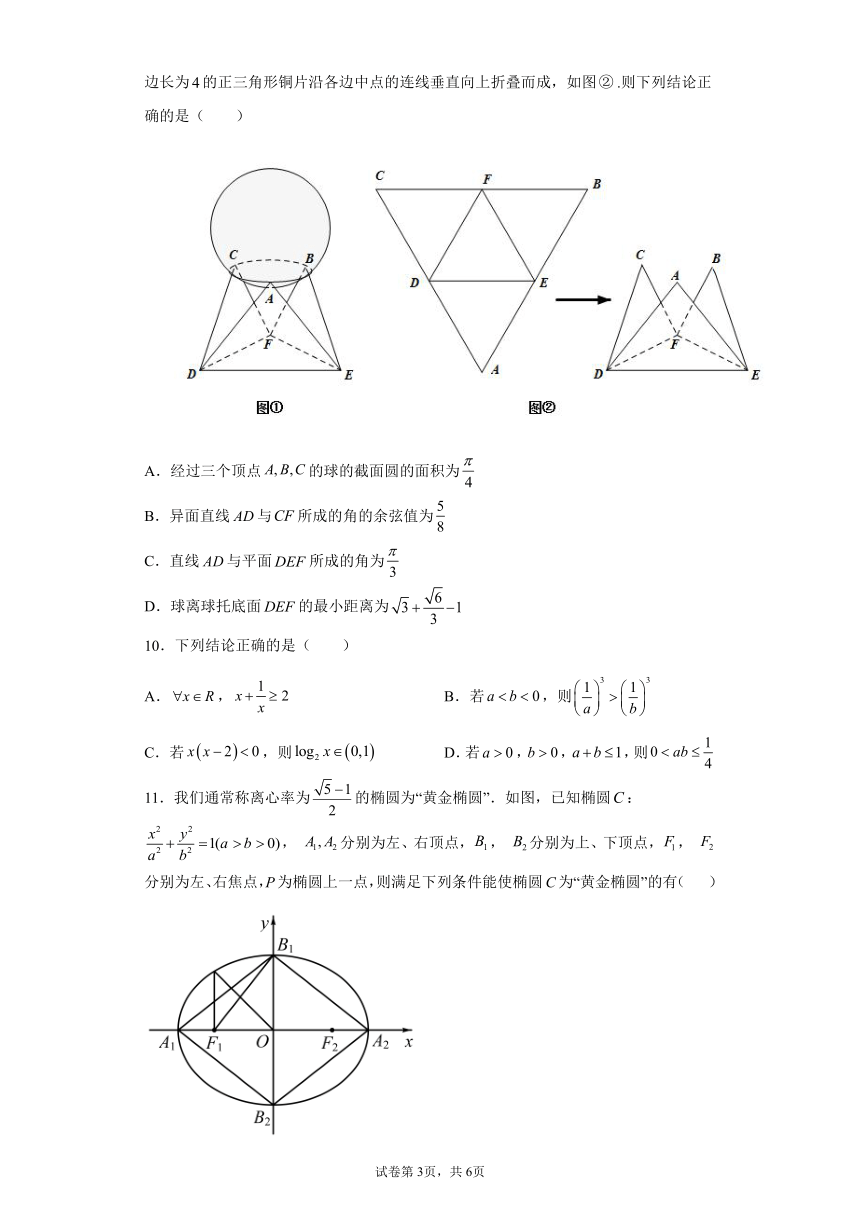
边长为 4的正三角形铜片沿各边中点的连线垂直向上折叠而成,如图② .则下列结论正
确的是( )
A.经过三个顶点 A,B,C的球的截面圆的面积为
4
5
B.异面直线 AD与CF所成的角的余弦值为
8
C.直线 AD与平面DEF所成的角为
3
D 6.球离球托底面DEF的最小距离为 3 1
3
10.下列结论正确的是( )
1 3 3
A x R x 2 B a b 0 1 1 . , .若 ,则
x a b
C.若 x x 2 0,则 log2 x 0,1 D.若 a 0
1
,b 0,a b 1,则0 ab
4
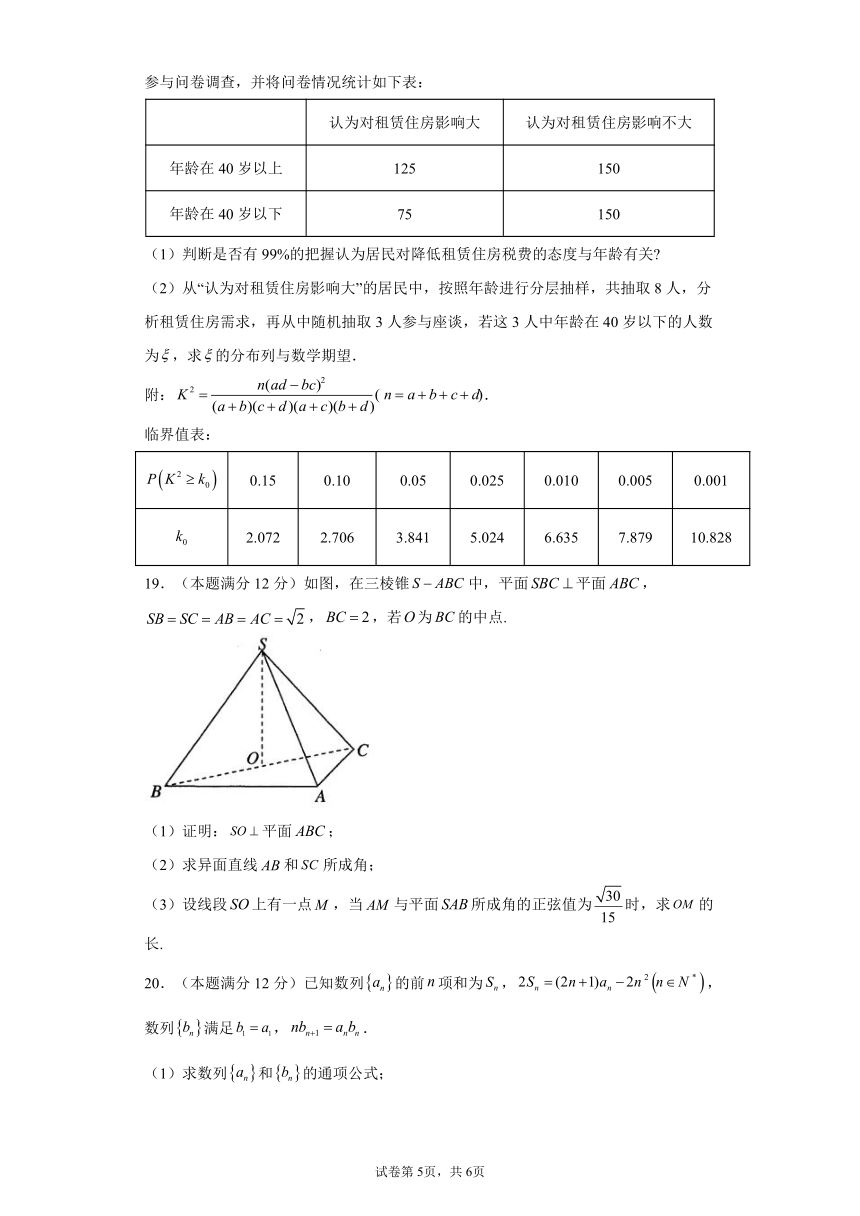
11 5 1.我们通常称离心率为 的椭圆为“黄金椭圆”.如图,已知椭圆C:
2
x2 y2
2 2 1(a b 0), A1, A2 分别为左、右顶点,B1, Ba b 2
分别为上、下顶点,F1, F2
分别为左、右焦点,P为椭圆上一点,则满足下列条件能使椭圆C为“黄金椭圆”的有( )
试卷第 3页,共 6页
A. A1F1 F2A2 F1F
2
2 B. F1B1A2 90
C. PF1 x轴,且 PO//A2B1 D.四边形 A1B2A2B1的内切圆过焦点 F1, F2
12.已知函数 f x ln x ax 1 a R ,则下列说法正确的是( )
A.若 f x 极大值为 0,则 a 2
B.当 a 0时, f x 在 0, 上单调递增
1
C. a 0时, f x x 1恒成立
2
D.若 a 1 2,则g x x 1 f x 有两个零点
第 II 卷(非选择题)
三、填空题(本题共 4小题,每小题 5分,共 20分.)
sin 1 cos
1 , 0, 5 13.已知 , , ,则 cos
________.3 6 5 4 3
uuur uuur uuur uuur uuur
14.已知向量 AB与 AC 的夹角为60 ,且 AB AC 2,若 AP AB AC 且 AP BC,
则实数 的值为________.
1 1
15 2.设 a b c 0,则 2a 10ac 25c2ab a(a b) 的最小值为________.
16.已知函数 f x 满足 f x f 3x ,当 x 1,3 时, f x ln x,若在区间 1,9
内,函数 g x f x ax有三个不同零点,则实数 a的取值范围为________.
四、解答题(本题共 6小题,共 70分.解答应写出文字说明、证明过程或演算步骤.)
17.(本题满分 10分)在①b sin B c sinC
2 3
b sinC a sin A;
3
② cos2 C sin B sinC sin2 B cos2 A;③2b 2acosC c这三个条件中任选一个,补充
在下面的问题中并作答.
在 ABC中,角A、 B、C所对的边分别是 a、b、c,______.
(1)求角A;
(2)若 a 10, ABC的面积为8 3,求 ABC的周长.
18.(本题满分 12分)2020年 12月 16日至 18日,中央经济工作会议在北京召开.会
议指出,近期社会上对于房屋租赁市场的一些乱象讨论颇多,此次会议也明确提出,要
降低租赁住房税费负担,整顿租赁市场秩序,规范市场行为,对租金水平进行合理调
控.为了解居民对降低租赁住房税费的态度,某社区居委会随机抽取了 500名社区居民
试卷第 4页,共 6页
参与问卷调查,并将问卷情况统计如下表:
认为对租赁住房影响大 认为对租赁住房影响不大
年龄在 40岁以上 125 150
年龄在 40岁以下 75 150
(1)判断是否有 99%的把握认为居民对降低租赁住房税费的态度与年龄有关
(2)从“认为对租赁住房影响大”的居民中,按照年龄进行分层抽样,共抽取 8人,分
析租赁住房需求,再从中随机抽取 3人参与座谈,若这 3人中年龄在 40岁以下的人数
为 ,求 的分布列与数学期望.
K 2 n(ad bc)
2
附: ( n a b c d).
(a b)(c d )(a c)(b d )
临界值表:
P K 2 k0 0.15 0.10 0.05 0.025 0.010 0.005 0.001
k0 2.072 2.706 3.841 5.024 6.635 7.879 10.828
19.(本题满分 12分)如图,在三棱锥 S ABC 中,平面 SBC 平面 ABC,
SB SC AB AC 2,BC 2,若O为 BC的中点.
(1)证明: SO 平面 ABC;
(2)求异面直线 AB和 SC 所成角;
(3)设线段 SO上有一点M ,当 AM 与平面 SAB 30所成角的正弦值为 时,求OM 的
15
长.
20 2 *.(本题满分 12分)已知数列 an 的前 n项和为 Sn, 2Sn (2n 1)an 2n n N ,
数列 bn 满足b1 a1, nbn 1 anbn.
(1)求数列 an 和 bn 的通项公式;
试卷第 5页,共 6页
a n 9 *
(2)设数列 n 的前 n项和为Tn,若不等式 b 2n
4 Tn n N 恒成立,求实数
n
的取值范围.
2
21 x.(本题满分 12分)如图,已知椭圆: y2 1,点A,B是它的两个顶点,过原
4
点且斜率为 k的直线 l与线段 AB相交于点D,且与椭圆相交于 E、 F 两点.
(Ⅰ)若 ED 6DF,求 k的值;
(Ⅱ)求四边形 AEBF 面积的最大值.
2
22.(本题满分 12分)已知函数 f (x) ax x 1(a R).e
(1)若函数 f (x)在区间 (1, )上单调递增,求实数 a的取值范围;
(2)当 a 0时,讨论函数 g(x) f (x) a 3的零点个数,并给予证明.
试卷第 6页,共 6页
2021-2022学年度高三阶段性检测参考答案
一、单项选择题(本题共 8 小题,每小题 5分,共 40分. 在每小题给出的四个选项中,只
有一项是符合题目要求.)
1—5 CDBAA 6—8 AAC
二、多项选择题(本题共 4 小题,每小题 5分,共 20分. 在每小题给出的四个选项中,有
多项符合题目要求,全部选对的得 5分,部分选对的得 2分,有选错的得 0分.)
9.BCD 10.BD 11.BD 12.BC
三、填空题(本题共 4小题,每小题 5分,共 20分.)
ln 3 1
13. 8 3 1 14.1 15.4 16. ,9 3e 15
四、解答题(本题共 6小题,共 70分.解答应写出文字说明、证明过程或演算步骤.)
17.(本题满分 10分)
2 3
解:(1)选择①:因为b sin B c sinC b sinC a sin A,
3
b2 2
2 3 2 3
所以由正弦定理可得 c b sinC a3
a,即b2 c2 a2 ab sinC ,
3
2 3
则由余弦定理可得 2bc cos A ab sinC 3,所以 sinC cos A sin AsinC.
3 3
C 0, ,则 sinC 0,所以 cos A 3 sin A,即 tan A 3,
3
因为 A 0, ,所以 A ;
3
选择②:由 cos2 C sin B sinC sin2 B cos2 A,
得1 sin2 C sin B sinC sin2 B 1 sin2 A,
即 sin2 B sin2 C sin2 A sin B sinC,
2 2 2
2 2 2 cos A b c a 1由正弦定理得b c a bc,由余弦定理得 .2bc 2
A 0, A 因为 ,所以 ;
3
选择③:由 2b 2acosC c,结合正弦定理得 2sin B 2sin AcosC sinC.
因为 A B C ,所以 sin B sin A C sin A C ,
则2sin A C 2 sin AcosC cos AsinC 2sin AcosC sinC,所以 2cos AsinC sinC.
因为C 0, 1,所以 sinC 0,故 cos A .
2
答案第 1页,共 7页
因为 A 0, ,所以 A ;
3
(2)由(1)知 A .
3
S 1 1 因为 △ABC bc sin A bc sin 8 3,所以bc 32.2 2 3
由余弦定理得, a2 b2 c2 2bc cosA b c 2 3bc ,
即 b c 2 a2 3bc 100 3 32 196,所以b c 14,
所以 ABC的周长为 a b c 24.
18.(本题满分 12分)
解:(1)由题意建立 2 2列联表如下:
认为对租赁住房影响大 认为对租赁住房影响不大 合计
年龄在 40岁以上 125 150 275
年龄在 40岁以下 75 150 225
合计 200 300 500
设H0:居民对降低租赁住房税费的态度与年龄无关
2
K 2 500 (125 150 75 150) 7.576 6.635,
200 300 275 225
所以有 99%的把握认为居民对降低租赁住房税费的态度与年龄有关.
(2)由题意可知,分层抽样抽取的 8人中,年龄在 40岁以上的有 5人,年龄在 40岁以下
的有 3人,则随机变量 的所有可能取值为 0,1,2,3.
3
P( 0) C5 5 C
2C1 15
3 , P( 1)
5 3 ,
C8 28 C
3
8 28
1 2 3
P( 2) C C 5 3 153 ,P( 3)
C 1
3
C 56 C3
,
8 8 56
所以随机变量 的分布列为
0 1 2 3
5 15 15 1
P
28 28 56 56
答案第 2页,共 7页
E( ) 0 5 1 15 2 15 3 1 9 .
28 28 56 56 8
19.(本题满分 12分)
解:(1)∵ SB SC, BO OC,
∴ SO BC,
∵平面 SBC 平面 ABC,
平面 SBC I平面 ABC BC,
SO 平面 SBC,
∴ SO 平面 SBC .
(2)∵ SB SC AB AC 2,BC 2,
∴BS CS,BA CA,
如图,分别以OB,OA,OC为 x轴, y轴, z轴的
非负半轴,建立空间直角坐标系,
∵ A 0,1,0 , B 1,0,0 , S 0,0,1 ,C 1,0,0 ,
uuur uur
∴ AB 1, 1,0 , SC 1,0, 1 ,
uuur uur
uuur uur AB SC
∵ cos AB,SC
1 1
uuur uur ,
AB SC 2 2 2
∴异面直线 AB和 SC 所成角为 .
3
(3)设m a,b,c 为平面 SBA的法向量,
uuur uur
∵ AB 1, 1,0 , SB 1,0, 1 ,
a b 0
∴ ,即m 1,1,1 ,
a c 0
设M 0,0, t , t 0,1 ,
uuur
∴ AM 0, 1, t ,
设 AM 与平面 SAB所成角为 ,
ur uuur
ur uuur m AM
∵sin cos m, AM ur uuur ,
m AM
答案第 3页,共 7页
30 t 1
∴ ,
15 3 1 t 2
6 6t 2 15 t 2 2t 1 ,
3t 2 10t 3 0,
t 3 3t 1 0,
1
t 3(舍), t ,
3
1
∴OM 的长为 .
3
20.(本题满分 12分)
2 *
解:(1)∵ 2Sn (2n 1)an 2n n N
∴当 n=1时, 2a1=3a1 2, a1=2 ,
2Sn= 2n+1 a 2n
2
当n 2 n时,由 ,
2Sn 1= 2n 1 an 1 2(n 1)
2
得2an= 2n+1 an 2n 1 an 1 2n2+2(n 1)2,即 an an 1=2,
数列 an 是公差为 2的等差数列,
a1=2, an=2n.
由条件得b1=2,nbn+1=2nbn, bn+1=2bn ,即数列 bn 是公比为 2的等比数列,
bn=2
n
;
an 2n n 2 3 4 n
(2)∵ = =b 2n 2n 1 ,则
Tn=1+ + 2 + 3+ + n 1 ,
n 2 2 2 2
1 T 1 2 3 n 1 n = + + + + + ,
2 n 2 22 23 2n 1 2n
答案第 4页,共 7页
1
1 1 n
Tn=1
1 1 1 1 n+ + + + + = 2 n =2 n+2 ,
2 2 2 2 2 3 2 n 1 2 n 1 1 2
n 2 n
2
T n+2 n=4 2n 1
,
n 9 n 4 Tn n N * 恒成立,2
n+9 n+2 n 5
则 4 n 4+2 2n 1
= n 恒成立,2
n 5 n 4 n 5 n+6
令 f n = n ,则 f n+1 f n =2 2n =+1 2n 2n+1 ,
f 1 <f 2 < <f 6 =f 7 >f 8 > ,
1
f (n)max=f 6 =f 7 = ,64
1
,
64
1
故实数 的取值范围是 ,+ ﹒ 64
21.(本题满分 12分)
x2
解:(1)椭圆: y2 1, A(2,0), B(0,1),
4
直线 AB, EF 的方程分别为 x 2y 2, y kx(k 0).
如图,设 D(x0 , kx0 ), E(x1, kx1), F (x2 , kx2 ),其中 x1 x2,
且 x1, x2满足方程 (1 4k 2 )x2 4,
x 2故 2 x1
1 4k 2
.①
1 5 10
由ED 6DF,知 x0 x1 6(x2 x0 ),得 x0 (6x2 x1) x2 7 7 ,7 1 4k 2
2
由D在 AB上知 x0 2kx0 2,得 x0 ,1 2k
10 2
所以 ,
7 1 4k 2 1 2k
化简得24k 2 25k 6 0,
答案第 5页,共 7页
2 3
解得 k 或 k .
3 8
(2)由题设, BO 1, | AO | 2.
由(Ⅰ)知, E(x1, kx1), F (x2 , kx2 ),
不妨设 y1 kx1, y2 kx2,由①得 x2 0,
根据 E与 F 关于原点对称可知 y2 y1 0,
故四边形 AEBF的面积为 S S OBE S OBF S OAE S OAF
1
OB ·( x1)
1 OB ·x 1 OA·y 1 OA·( y )
2 2 2 2 2 2 1
1 OB (x 1 2 x1) OA (y2 y1) x2 2y2 2 2
(x2 2y2 )
2 x 22 4y
2
2 4x2 y2 2(x 22 4y 22 ) 2 2,
当 x2 2y2时,上式取等号.所以S的最大值为 2 2.
22.(本题满分 12分)
解:(1) f (x) a
2
ex
2
由题意得 f (x) 0,即 a 在区间 (1, )上恒成立.
ex
当 x (1, )
2 2 2
时, x 0, ,所以 a ,e e e
2
故实数 a的取值范围为 , e
.
2
(2)由已知得 g(x) ax a 2,
ex
2 aex 2
则 g (x) a x e ex
.
当 a 0时, g (x) 0,函数 g(x)单调递减,
又 g(0) a 0 g(1)
2
, 2 0,故函数 g(x)有且只有一个零点.
e
2
当 a 0时,令 g (x) 0,得 x ln ,函数 g(x)单调递减,
a
令 g (x) 0,得 x ln
2
,函数 g(x)单调递增,
a
g ln 2 a ln 2 2 而 0, g
a 2 2
a 2 0,
a a a a e a
答案第 6页,共 7页
( ln x x在 (0, )上恒成立)
a 2 2 2 a 2
由于 x ln x,所以 ln
2
,所以 g(x) 在 ln ,
上存在一个零点.
a a a a a
g
ln 2 a a lna
2 a 2
ln 2 2又 2 ,且 2 ln , a a 2 2 a a 2 a
2 2
设 h(a) a ln a a 2 h (a) 1 2a 1 a a 1 ,则 0 在 (0, )上恒成立,
2 a2 a 2 a2 a 2
故 h(a)在 (0, )上单调递增.
2
而h(0) 0,所以 h(a) 0在 (0, )上恒成立,所以 g ln 2 0, a a 2
所以 g(x) 在 ln
2
2 , ln
2
上存在一个零点.
a a 2 a
综上所述,当 a 0时,函数 g(x)有且只有一个零点;当 a 0时,函数 g(x)有两个零点.
答案第 7页,共 7页
数学
本试卷共 6页,共 150分,考试时间 120分钟
注意事项:
1.答题前,考生先将自己的姓名、考生号、座号填写在相应位置,认真核对条形码上的
姓名、考生号和座号,并将条形码粘贴在指定位置上。
2.选择题答案必须使用 2B铅笔(按填涂样例)正确填涂,非选择题答案必须使用 0. 5
毫米黑色签字笔书写,字体工整、笔迹清楚。
3.请按照题号在各题目的答题区域内作答,超出答题区域书写的答案无效;在草稿纸、
试题卷上答题无效。保持卡面清洁,不折叠、不破损。
第 I 卷(选择题)
一、单项选择题(本题共 8小题,每小题 5分,共 40分. 在每小题给出的四个选项中,
只有一项是符合题目要求.)
1.已知集合M {x | y ln(x 1)} . N y | y ex ,则M N ( )
A. ( 1,0) B. ( 1, ) C. (0, ) D. R
1
2.如图,若向量OZ对应的复数为 z,且 z 5,则 ( )z
1 2 i 1 2 i 1 2 1 2A. B. C. i D. i
5 5 5 5 5 5 5 5
2 13. (x 2 2)
3
展开式中的常数项为
x
A. 20 B. 20 C. 12 D. 8
4.函数 y cos x ln | x |的图象可能是( )
A. B.
C. D.
5.斐波那契螺旋线被誉为自然界最完美的“黄金螺旋”,它的画法是:以斐波那契数:
试卷第 1页,共 6页
1,1,2,3,5,…为边的正方形拼成长方形,然后在每个正方形中画一个圆心角为90 的圆
弧,这些圆弧所连起来的弧线就是斐波那契螺旋线.自然界存在很多斐波拉契螺旋线的
图案,例如向日葵、鹦鹉螺等.右图为该螺旋线的前一部分,如果用接下来的一段圆弧
所对应的扇形做圆锥的侧面则该圆锥的体积为( )
A 8 15π. B 4 15 C 125 15 D 125 15 . . .
3 3 192 64
6.已知函数 f (x) 2 sin x和 g(x) 2 cos x( 0)图象的交点中,任意连续三
个交点均可作为一个等腰直角三角形的顶点.为了得到 y g(x)的图象,只需把 y f (x)
的图象( )
A.向左平移 1个单位 B.向左平移 个单位
2
C.向右平移 1个单位 D.向右平移 个单位
2
7.在 ABC中,角A,B,C所对应的边分别为 a,b,c,若 ac 4,sin B 2sinC cos A 0,
则 ABC面积的最大值为
A.1 B. 3 C.2 D. 4
8.已知 F1,F2是椭圆与双曲线的公共焦点,P是它们的一个公共点,且 PF1 PF2 ,线
2 e2
段 PF1的垂直平分线过 F2,若椭圆的离心率为 e1,双曲线的离心率为 e2,则 e 的最1 2
小值为( )
A. 6 B.3 C.6 D. 3
二、多项选择题(本题共 4小题,每小题 5分,共 20分. 在每小题给出的四个选项中,
有多项符合题目要求,全部选对的得 5分,部分选对的得 2分,有选错的得 0分.)
9.为弘扬中华民族优秀传统文化,某学校组织了《诵经典,获新知》的演讲比赛,本
4
次比赛的冠军奖杯由一个铜球和一个托盘组成,如图①,已知球的体积为 ,托盘由
3
试卷第 2页,共 6页
边长为 4的正三角形铜片沿各边中点的连线垂直向上折叠而成,如图② .则下列结论正
确的是( )
A.经过三个顶点 A,B,C的球的截面圆的面积为
4
5
B.异面直线 AD与CF所成的角的余弦值为
8
C.直线 AD与平面DEF所成的角为
3
D 6.球离球托底面DEF的最小距离为 3 1
3
10.下列结论正确的是( )
1 3 3
A x R x 2 B a b 0 1 1 . , .若 ,则
x a b
C.若 x x 2 0,则 log2 x 0,1 D.若 a 0
1
,b 0,a b 1,则0 ab
4
11 5 1.我们通常称离心率为 的椭圆为“黄金椭圆”.如图,已知椭圆C:
2
x2 y2
2 2 1(a b 0), A1, A2 分别为左、右顶点,B1, Ba b 2
分别为上、下顶点,F1, F2
分别为左、右焦点,P为椭圆上一点,则满足下列条件能使椭圆C为“黄金椭圆”的有( )
试卷第 3页,共 6页
A. A1F1 F2A2 F1F
2
2 B. F1B1A2 90
C. PF1 x轴,且 PO//A2B1 D.四边形 A1B2A2B1的内切圆过焦点 F1, F2
12.已知函数 f x ln x ax 1 a R ,则下列说法正确的是( )
A.若 f x 极大值为 0,则 a 2
B.当 a 0时, f x 在 0, 上单调递增
1
C. a 0时, f x x 1恒成立
2
D.若 a 1 2,则g x x 1 f x 有两个零点
第 II 卷(非选择题)
三、填空题(本题共 4小题,每小题 5分,共 20分.)
sin 1 cos
1 , 0, 5 13.已知 , , ,则 cos
________.3 6 5 4 3
uuur uuur uuur uuur uuur
14.已知向量 AB与 AC 的夹角为60 ,且 AB AC 2,若 AP AB AC 且 AP BC,
则实数 的值为________.
1 1
15 2.设 a b c 0,则 2a 10ac 25c2ab a(a b) 的最小值为________.
16.已知函数 f x 满足 f x f 3x ,当 x 1,3 时, f x ln x,若在区间 1,9
内,函数 g x f x ax有三个不同零点,则实数 a的取值范围为________.
四、解答题(本题共 6小题,共 70分.解答应写出文字说明、证明过程或演算步骤.)
17.(本题满分 10分)在①b sin B c sinC
2 3
b sinC a sin A;
3
② cos2 C sin B sinC sin2 B cos2 A;③2b 2acosC c这三个条件中任选一个,补充
在下面的问题中并作答.
在 ABC中,角A、 B、C所对的边分别是 a、b、c,______.
(1)求角A;
(2)若 a 10, ABC的面积为8 3,求 ABC的周长.
18.(本题满分 12分)2020年 12月 16日至 18日,中央经济工作会议在北京召开.会
议指出,近期社会上对于房屋租赁市场的一些乱象讨论颇多,此次会议也明确提出,要
降低租赁住房税费负担,整顿租赁市场秩序,规范市场行为,对租金水平进行合理调
控.为了解居民对降低租赁住房税费的态度,某社区居委会随机抽取了 500名社区居民
试卷第 4页,共 6页
参与问卷调查,并将问卷情况统计如下表:
认为对租赁住房影响大 认为对租赁住房影响不大
年龄在 40岁以上 125 150
年龄在 40岁以下 75 150
(1)判断是否有 99%的把握认为居民对降低租赁住房税费的态度与年龄有关
(2)从“认为对租赁住房影响大”的居民中,按照年龄进行分层抽样,共抽取 8人,分
析租赁住房需求,再从中随机抽取 3人参与座谈,若这 3人中年龄在 40岁以下的人数
为 ,求 的分布列与数学期望.
K 2 n(ad bc)
2
附: ( n a b c d).
(a b)(c d )(a c)(b d )
临界值表:
P K 2 k0 0.15 0.10 0.05 0.025 0.010 0.005 0.001
k0 2.072 2.706 3.841 5.024 6.635 7.879 10.828
19.(本题满分 12分)如图,在三棱锥 S ABC 中,平面 SBC 平面 ABC,
SB SC AB AC 2,BC 2,若O为 BC的中点.
(1)证明: SO 平面 ABC;
(2)求异面直线 AB和 SC 所成角;
(3)设线段 SO上有一点M ,当 AM 与平面 SAB 30所成角的正弦值为 时,求OM 的
15
长.
20 2 *.(本题满分 12分)已知数列 an 的前 n项和为 Sn, 2Sn (2n 1)an 2n n N ,
数列 bn 满足b1 a1, nbn 1 anbn.
(1)求数列 an 和 bn 的通项公式;
试卷第 5页,共 6页
a n 9 *
(2)设数列 n 的前 n项和为Tn,若不等式 b 2n
4 Tn n N 恒成立,求实数
n
的取值范围.
2
21 x.(本题满分 12分)如图,已知椭圆: y2 1,点A,B是它的两个顶点,过原
4
点且斜率为 k的直线 l与线段 AB相交于点D,且与椭圆相交于 E、 F 两点.
(Ⅰ)若 ED 6DF,求 k的值;
(Ⅱ)求四边形 AEBF 面积的最大值.
2
22.(本题满分 12分)已知函数 f (x) ax x 1(a R).e
(1)若函数 f (x)在区间 (1, )上单调递增,求实数 a的取值范围;
(2)当 a 0时,讨论函数 g(x) f (x) a 3的零点个数,并给予证明.
试卷第 6页,共 6页
2021-2022学年度高三阶段性检测参考答案
一、单项选择题(本题共 8 小题,每小题 5分,共 40分. 在每小题给出的四个选项中,只
有一项是符合题目要求.)
1—5 CDBAA 6—8 AAC
二、多项选择题(本题共 4 小题,每小题 5分,共 20分. 在每小题给出的四个选项中,有
多项符合题目要求,全部选对的得 5分,部分选对的得 2分,有选错的得 0分.)
9.BCD 10.BD 11.BD 12.BC
三、填空题(本题共 4小题,每小题 5分,共 20分.)
ln 3 1
13. 8 3 1 14.1 15.4 16. ,9 3e 15
四、解答题(本题共 6小题,共 70分.解答应写出文字说明、证明过程或演算步骤.)
17.(本题满分 10分)
2 3
解:(1)选择①:因为b sin B c sinC b sinC a sin A,
3
b2 2
2 3 2 3
所以由正弦定理可得 c b sinC a3
a,即b2 c2 a2 ab sinC ,
3
2 3
则由余弦定理可得 2bc cos A ab sinC 3,所以 sinC cos A sin AsinC.
3 3
C 0, ,则 sinC 0,所以 cos A 3 sin A,即 tan A 3,
3
因为 A 0, ,所以 A ;
3
选择②:由 cos2 C sin B sinC sin2 B cos2 A,
得1 sin2 C sin B sinC sin2 B 1 sin2 A,
即 sin2 B sin2 C sin2 A sin B sinC,
2 2 2
2 2 2 cos A b c a 1由正弦定理得b c a bc,由余弦定理得 .2bc 2
A 0, A 因为 ,所以 ;
3
选择③:由 2b 2acosC c,结合正弦定理得 2sin B 2sin AcosC sinC.
因为 A B C ,所以 sin B sin A C sin A C ,
则2sin A C 2 sin AcosC cos AsinC 2sin AcosC sinC,所以 2cos AsinC sinC.
因为C 0, 1,所以 sinC 0,故 cos A .
2
答案第 1页,共 7页
因为 A 0, ,所以 A ;
3
(2)由(1)知 A .
3
S 1 1 因为 △ABC bc sin A bc sin 8 3,所以bc 32.2 2 3
由余弦定理得, a2 b2 c2 2bc cosA b c 2 3bc ,
即 b c 2 a2 3bc 100 3 32 196,所以b c 14,
所以 ABC的周长为 a b c 24.
18.(本题满分 12分)
解:(1)由题意建立 2 2列联表如下:
认为对租赁住房影响大 认为对租赁住房影响不大 合计
年龄在 40岁以上 125 150 275
年龄在 40岁以下 75 150 225
合计 200 300 500
设H0:居民对降低租赁住房税费的态度与年龄无关
2
K 2 500 (125 150 75 150) 7.576 6.635,
200 300 275 225
所以有 99%的把握认为居民对降低租赁住房税费的态度与年龄有关.
(2)由题意可知,分层抽样抽取的 8人中,年龄在 40岁以上的有 5人,年龄在 40岁以下
的有 3人,则随机变量 的所有可能取值为 0,1,2,3.
3
P( 0) C5 5 C
2C1 15
3 , P( 1)
5 3 ,
C8 28 C
3
8 28
1 2 3
P( 2) C C 5 3 153 ,P( 3)
C 1
3
C 56 C3
,
8 8 56
所以随机变量 的分布列为
0 1 2 3
5 15 15 1
P
28 28 56 56
答案第 2页,共 7页
E( ) 0 5 1 15 2 15 3 1 9 .
28 28 56 56 8
19.(本题满分 12分)
解:(1)∵ SB SC, BO OC,
∴ SO BC,
∵平面 SBC 平面 ABC,
平面 SBC I平面 ABC BC,
SO 平面 SBC,
∴ SO 平面 SBC .
(2)∵ SB SC AB AC 2,BC 2,
∴BS CS,BA CA,
如图,分别以OB,OA,OC为 x轴, y轴, z轴的
非负半轴,建立空间直角坐标系,
∵ A 0,1,0 , B 1,0,0 , S 0,0,1 ,C 1,0,0 ,
uuur uur
∴ AB 1, 1,0 , SC 1,0, 1 ,
uuur uur
uuur uur AB SC
∵ cos AB,SC
1 1
uuur uur ,
AB SC 2 2 2
∴异面直线 AB和 SC 所成角为 .
3
(3)设m a,b,c 为平面 SBA的法向量,
uuur uur
∵ AB 1, 1,0 , SB 1,0, 1 ,
a b 0
∴ ,即m 1,1,1 ,
a c 0
设M 0,0, t , t 0,1 ,
uuur
∴ AM 0, 1, t ,
设 AM 与平面 SAB所成角为 ,
ur uuur
ur uuur m AM
∵sin cos m, AM ur uuur ,
m AM
答案第 3页,共 7页
30 t 1
∴ ,
15 3 1 t 2
6 6t 2 15 t 2 2t 1 ,
3t 2 10t 3 0,
t 3 3t 1 0,
1
t 3(舍), t ,
3
1
∴OM 的长为 .
3
20.(本题满分 12分)
2 *
解:(1)∵ 2Sn (2n 1)an 2n n N
∴当 n=1时, 2a1=3a1 2, a1=2 ,
2Sn= 2n+1 a 2n
2
当n 2 n时,由 ,
2Sn 1= 2n 1 an 1 2(n 1)
2
得2an= 2n+1 an 2n 1 an 1 2n2+2(n 1)2,即 an an 1=2,
数列 an 是公差为 2的等差数列,
a1=2, an=2n.
由条件得b1=2,nbn+1=2nbn, bn+1=2bn ,即数列 bn 是公比为 2的等比数列,
bn=2
n
;
an 2n n 2 3 4 n
(2)∵ = =b 2n 2n 1 ,则
Tn=1+ + 2 + 3+ + n 1 ,
n 2 2 2 2
1 T 1 2 3 n 1 n = + + + + + ,
2 n 2 22 23 2n 1 2n
答案第 4页,共 7页
1
1 1 n
Tn=1
1 1 1 1 n+ + + + + = 2 n =2 n+2 ,
2 2 2 2 2 3 2 n 1 2 n 1 1 2
n 2 n
2
T n+2 n=4 2n 1
,
n 9 n 4 Tn n N * 恒成立,2
n+9 n+2 n 5
则 4 n 4+2 2n 1
= n 恒成立,2
n 5 n 4 n 5 n+6
令 f n = n ,则 f n+1 f n =2 2n =+1 2n 2n+1 ,
f 1 <f 2 < <f 6 =f 7 >f 8 > ,
1
f (n)max=f 6 =f 7 = ,64
1
,
64
1
故实数 的取值范围是 ,+ ﹒ 64
21.(本题满分 12分)
x2
解:(1)椭圆: y2 1, A(2,0), B(0,1),
4
直线 AB, EF 的方程分别为 x 2y 2, y kx(k 0).
如图,设 D(x0 , kx0 ), E(x1, kx1), F (x2 , kx2 ),其中 x1 x2,
且 x1, x2满足方程 (1 4k 2 )x2 4,
x 2故 2 x1
1 4k 2
.①
1 5 10
由ED 6DF,知 x0 x1 6(x2 x0 ),得 x0 (6x2 x1) x2 7 7 ,7 1 4k 2
2
由D在 AB上知 x0 2kx0 2,得 x0 ,1 2k
10 2
所以 ,
7 1 4k 2 1 2k
化简得24k 2 25k 6 0,
答案第 5页,共 7页
2 3
解得 k 或 k .
3 8
(2)由题设, BO 1, | AO | 2.
由(Ⅰ)知, E(x1, kx1), F (x2 , kx2 ),
不妨设 y1 kx1, y2 kx2,由①得 x2 0,
根据 E与 F 关于原点对称可知 y2 y1 0,
故四边形 AEBF的面积为 S S OBE S OBF S OAE S OAF
1
OB ·( x1)
1 OB ·x 1 OA·y 1 OA·( y )
2 2 2 2 2 2 1
1 OB (x 1 2 x1) OA (y2 y1) x2 2y2 2 2
(x2 2y2 )
2 x 22 4y
2
2 4x2 y2 2(x 22 4y 22 ) 2 2,
当 x2 2y2时,上式取等号.所以S的最大值为 2 2.
22.(本题满分 12分)
解:(1) f (x) a
2
ex
2
由题意得 f (x) 0,即 a 在区间 (1, )上恒成立.
ex
当 x (1, )
2 2 2
时, x 0, ,所以 a ,e e e
2
故实数 a的取值范围为 , e
.
2
(2)由已知得 g(x) ax a 2,
ex
2 aex 2
则 g (x) a x e ex
.
当 a 0时, g (x) 0,函数 g(x)单调递减,
又 g(0) a 0 g(1)
2
, 2 0,故函数 g(x)有且只有一个零点.
e
2
当 a 0时,令 g (x) 0,得 x ln ,函数 g(x)单调递减,
a
令 g (x) 0,得 x ln
2
,函数 g(x)单调递增,
a
g ln 2 a ln 2 2 而 0, g
a 2 2
a 2 0,
a a a a e a
答案第 6页,共 7页
( ln x x在 (0, )上恒成立)
a 2 2 2 a 2
由于 x ln x,所以 ln
2
,所以 g(x) 在 ln ,
上存在一个零点.
a a a a a
g
ln 2 a a lna
2 a 2
ln 2 2又 2 ,且 2 ln , a a 2 2 a a 2 a
2 2
设 h(a) a ln a a 2 h (a) 1 2a 1 a a 1 ,则 0 在 (0, )上恒成立,
2 a2 a 2 a2 a 2
故 h(a)在 (0, )上单调递增.
2
而h(0) 0,所以 h(a) 0在 (0, )上恒成立,所以 g ln 2 0, a a 2
所以 g(x) 在 ln
2
2 , ln
2
上存在一个零点.
a a 2 a
综上所述,当 a 0时,函数 g(x)有且只有一个零点;当 a 0时,函数 g(x)有两个零点.
答案第 7页,共 7页
同课章节目录
