沪科版数学九年级上册 23.2 解直角三角形及其应用(教案)
文档属性
| 名称 | 沪科版数学九年级上册 23.2 解直角三角形及其应用(教案) |

|
|
| 格式 | doc | ||
| 文件大小 | 186.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-12-28 00:00:00 | ||
图片预览

文档简介
解直角三角形及其应用
【教学目标】
1.熟练掌握直角三角形除直角外五个元素之间的关系。
2.学会根据题目要求正确地选用这些关系式解直角三角形。
【教学重点】
会利用已知条件解直角三角形。
【教学难点】
根据题目要求正确选用适当的三角关系式解直角三角形。
【课时安排】
4课时。
【教学过程】
【第一课时】
一、复习回顾:
(一)直角三角形三边的关系:勾股定理a2+b2=c2。
(二)直角三角形两锐角的关系:两锐角互余∠A+∠B=90°。
(三)直角三角形边与角之间的关系:锐角三角函数。
(四)互余两角之间的三角函数关系:
同角之间的三角函数关系:
特殊角30°、45°、60°角的三角函数值。
二、新课探究:
有以上的关系,如果知道了五个元素中的两个元素(至少有一个是边),就可以求出其余的三个元素。
在直角三角形中,除直角外,由已知元素求出未知元素的过程,叫做解直角三角形。
例1:在RT△ABC中,∠C=90°,∠B=42°6′,c=287.4,解这个三角形。
解:∠A=90°-42°6′=47°54′,a=c·cosB=287.4×0.7420=213.3;
b=c·sinB=287.4×0.6704=192.7。
三、练习:
(一)在RT△ABC中,∠C=90°,AC=6,∠BAC的平分线AD=,解此直角三角形。
(二)已知AB=4,∠B=45°,∠C=30°,求△ABC其余各边的长,各角的度数和△ABC的面积。
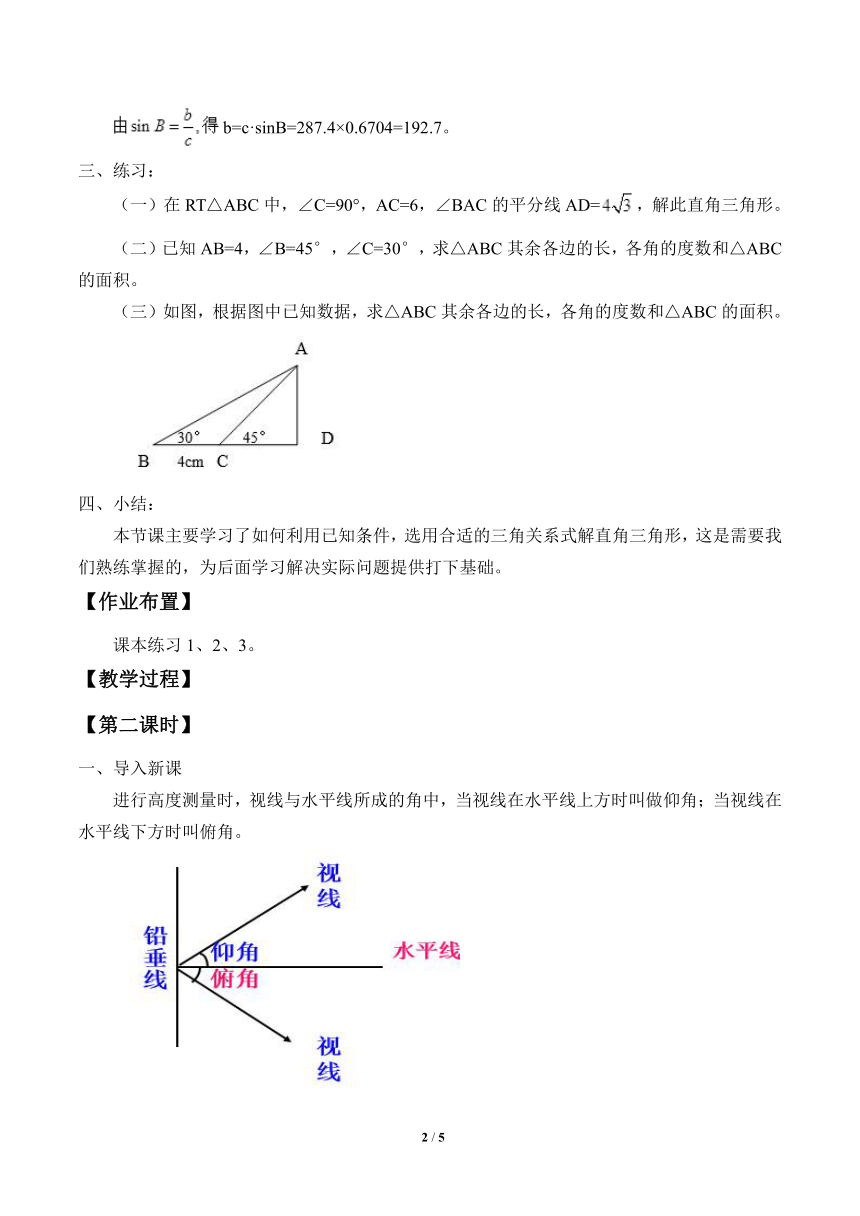
(三)如图,根据图中已知数据,求△ABC其余各边的长,各角的度数和△ABC的面积。
四、小结:
本节课主要学习了如何利用已知条件,选用合适的三角关系式解直角三角形,这是需要我们熟练掌握的,为后面学习解决实际问题提供打下基础。
【作业布置】
课本练习1、2、3。
【教学过程】
【第二课时】
一、导入新课
进行高度测量时,视线与水平线所成的角中,当视线在水平线上方时叫做仰角;当视线在水平线下方时叫俯角。
二、新课讲解:
例3:一学生要测量校园内一棵水杉树的高度,他站在距离水杉树8m的E处,测得树顶的仰角∠ACD=52°,已知测角仪的架高CE=1.6m,求树高AB。(精确到0.1m)
解:在Rt⊿ACD中,∠ACD=520,CD=EB=8m.;
由tan∠ACD=,得
AD=CD·tan∠ACD=8tan520=8×1.2799≈10.2(m);
又DB=CE=1.6m,得
AB=AD+DB=10.2+1.6=11.8m;
∴树高约为11.8m。
练习:飞机飞行的高度AB=1000m,从飞机上测得地面上跑道着地点C的俯角为18°,求飞机A到着地点C的距离。(精确到1m)。
例4:如图,要测量铁塔的高AB,在地面上选取一点C,在AC两点间选取一点D,测得CD=50米,在C、D两点处分别用测角仪测得铁塔顶端B的仰角为α=30°和β=45°。测角仪支架的高为1米,求铁塔的高(精确到0.1米)。
解:略。
课堂练习:
在与旗杆AB相距20m的C处,用高1.2m的测角仪测得旗杆的顶端B的仰角a=30°,求旗杆AB的高。(精确到0.1m)
【作业布置】
练习1、2。
【第三课时】
例5:某校九年级学生为了测量当地电视塔高AB,因为不能直接到塔底B处,他采用在发射塔院外与电视塔B成一直线的C、D两地面处,用测角器测得顶部A的仰角45°和30°,同时测得CD=50m,测角器高1m,你能求电视塔的高度吗?
解:设AB1=xm,在Rt⊿AC1B1中,由∠AC1B1=45°,得C1B1=AB1=x,又在Rt⊿AD1B1,中由∠AD1B1=30°,得:
tan∠AD1B1==,即tan30°=;
解方程,得x=25(+1)≈68(m);
∴AB=AB1+B1B≈68+1=69(m);
因而,电视塔的高约为69m。
练习:一船以20nm/h的速度向正东航行,在A处测得灯塔C在北偏东60°,继续航行1h到达B处,再测得灯塔C在北偏东30°,已知灯塔C四周10nm内有暗礁,问这船继续向东航行是否安全?
分析:这船继续向东航行是否安全,取决于灯塔到航线的距离是否大于10nm。
解:作CD⊥AB于点D,设CD=xnm;
在Rt⊿ACD中,AD==;
在Rt⊿BCD中,BD==;
由AB=AD-BD,得:
AB=-=20;
∴CD=x==10>10。
因而,船继续向东航行五触礁的危险。
例7:铁路路基的横断面是等腰梯形ABCD,路基的上底宽BC=9.8m,路基高BE=5.8m,斜坡的坡度1:1.6,求路基下底宽(精确到0.1m)与斜坡的坡角。
课堂练习:练习1、2。
【作业布置】
课本习题的2、3、5。
【第四课时】
例6.铁路路基的横断面是等腰梯形ABCD,路基的上底宽BC=9.8m,路基高BE=5.8m,斜坡的坡度1:1.6,求路基下底宽(精确到0.1m)与斜坡的坡角。
(解题过程略)
回顾解题思路,指导学生思考例7并求证,分小组写出求证过程,教师根据学生的解题过程展开讲解。
课堂练习:分别求直线y=+2的向上方向与x轴正方向和y轴正方向所夹的锐角。
【作业布置】
习题的6、8。
5 / 5
【教学目标】
1.熟练掌握直角三角形除直角外五个元素之间的关系。
2.学会根据题目要求正确地选用这些关系式解直角三角形。
【教学重点】
会利用已知条件解直角三角形。
【教学难点】
根据题目要求正确选用适当的三角关系式解直角三角形。
【课时安排】
4课时。
【教学过程】
【第一课时】
一、复习回顾:
(一)直角三角形三边的关系:勾股定理a2+b2=c2。
(二)直角三角形两锐角的关系:两锐角互余∠A+∠B=90°。
(三)直角三角形边与角之间的关系:锐角三角函数。
(四)互余两角之间的三角函数关系:
同角之间的三角函数关系:
特殊角30°、45°、60°角的三角函数值。
二、新课探究:
有以上的关系,如果知道了五个元素中的两个元素(至少有一个是边),就可以求出其余的三个元素。
在直角三角形中,除直角外,由已知元素求出未知元素的过程,叫做解直角三角形。
例1:在RT△ABC中,∠C=90°,∠B=42°6′,c=287.4,解这个三角形。
解:∠A=90°-42°6′=47°54′,a=c·cosB=287.4×0.7420=213.3;
b=c·sinB=287.4×0.6704=192.7。
三、练习:
(一)在RT△ABC中,∠C=90°,AC=6,∠BAC的平分线AD=,解此直角三角形。
(二)已知AB=4,∠B=45°,∠C=30°,求△ABC其余各边的长,各角的度数和△ABC的面积。
(三)如图,根据图中已知数据,求△ABC其余各边的长,各角的度数和△ABC的面积。
四、小结:
本节课主要学习了如何利用已知条件,选用合适的三角关系式解直角三角形,这是需要我们熟练掌握的,为后面学习解决实际问题提供打下基础。
【作业布置】
课本练习1、2、3。
【教学过程】
【第二课时】
一、导入新课
进行高度测量时,视线与水平线所成的角中,当视线在水平线上方时叫做仰角;当视线在水平线下方时叫俯角。
二、新课讲解:
例3:一学生要测量校园内一棵水杉树的高度,他站在距离水杉树8m的E处,测得树顶的仰角∠ACD=52°,已知测角仪的架高CE=1.6m,求树高AB。(精确到0.1m)
解:在Rt⊿ACD中,∠ACD=520,CD=EB=8m.;
由tan∠ACD=,得
AD=CD·tan∠ACD=8tan520=8×1.2799≈10.2(m);
又DB=CE=1.6m,得
AB=AD+DB=10.2+1.6=11.8m;
∴树高约为11.8m。
练习:飞机飞行的高度AB=1000m,从飞机上测得地面上跑道着地点C的俯角为18°,求飞机A到着地点C的距离。(精确到1m)。
例4:如图,要测量铁塔的高AB,在地面上选取一点C,在AC两点间选取一点D,测得CD=50米,在C、D两点处分别用测角仪测得铁塔顶端B的仰角为α=30°和β=45°。测角仪支架的高为1米,求铁塔的高(精确到0.1米)。
解:略。
课堂练习:
在与旗杆AB相距20m的C处,用高1.2m的测角仪测得旗杆的顶端B的仰角a=30°,求旗杆AB的高。(精确到0.1m)
【作业布置】
练习1、2。
【第三课时】
例5:某校九年级学生为了测量当地电视塔高AB,因为不能直接到塔底B处,他采用在发射塔院外与电视塔B成一直线的C、D两地面处,用测角器测得顶部A的仰角45°和30°,同时测得CD=50m,测角器高1m,你能求电视塔的高度吗?
解:设AB1=xm,在Rt⊿AC1B1中,由∠AC1B1=45°,得C1B1=AB1=x,又在Rt⊿AD1B1,中由∠AD1B1=30°,得:
tan∠AD1B1==,即tan30°=;
解方程,得x=25(+1)≈68(m);
∴AB=AB1+B1B≈68+1=69(m);
因而,电视塔的高约为69m。
练习:一船以20nm/h的速度向正东航行,在A处测得灯塔C在北偏东60°,继续航行1h到达B处,再测得灯塔C在北偏东30°,已知灯塔C四周10nm内有暗礁,问这船继续向东航行是否安全?
分析:这船继续向东航行是否安全,取决于灯塔到航线的距离是否大于10nm。
解:作CD⊥AB于点D,设CD=xnm;
在Rt⊿ACD中,AD==;
在Rt⊿BCD中,BD==;
由AB=AD-BD,得:
AB=-=20;
∴CD=x==10>10。
因而,船继续向东航行五触礁的危险。
例7:铁路路基的横断面是等腰梯形ABCD,路基的上底宽BC=9.8m,路基高BE=5.8m,斜坡的坡度1:1.6,求路基下底宽(精确到0.1m)与斜坡的坡角。
课堂练习:练习1、2。
【作业布置】
课本习题的2、3、5。
【第四课时】
例6.铁路路基的横断面是等腰梯形ABCD,路基的上底宽BC=9.8m,路基高BE=5.8m,斜坡的坡度1:1.6,求路基下底宽(精确到0.1m)与斜坡的坡角。
(解题过程略)
回顾解题思路,指导学生思考例7并求证,分小组写出求证过程,教师根据学生的解题过程展开讲解。
课堂练习:分别求直线y=+2的向上方向与x轴正方向和y轴正方向所夹的锐角。
【作业布置】
习题的6、8。
5 / 5
