人教版数学七年级下册5.2.2平行线及其判定 课件(共16张PPT)
文档属性
| 名称 | 人教版数学七年级下册5.2.2平行线及其判定 课件(共16张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 1.5MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-12-28 00:00:00 | ||
图片预览


文档简介
(共16张PPT)
新人教版-七年级(下)数学-第五章
5 .2.1 直线平行的条件(1)
一、学习目标
1、学会辨别同位角、内错角、同旁内角;
2、掌握“同位角相等,两直线平行”的条件,并能解决一些实际问题;
二、重点和难点
重点:探索两直线平行的条件
难点:同位角的寻找
回顾与思考
在同一平面内
相交
平行
二条直线的位置关系是:
的两条直线叫做平行线.
同一平面内,不相交
同一平面内
根据平行线的定义,两条直线平行必须符合
什么条件
——(1)同一平面内;
(2) 没有交点.
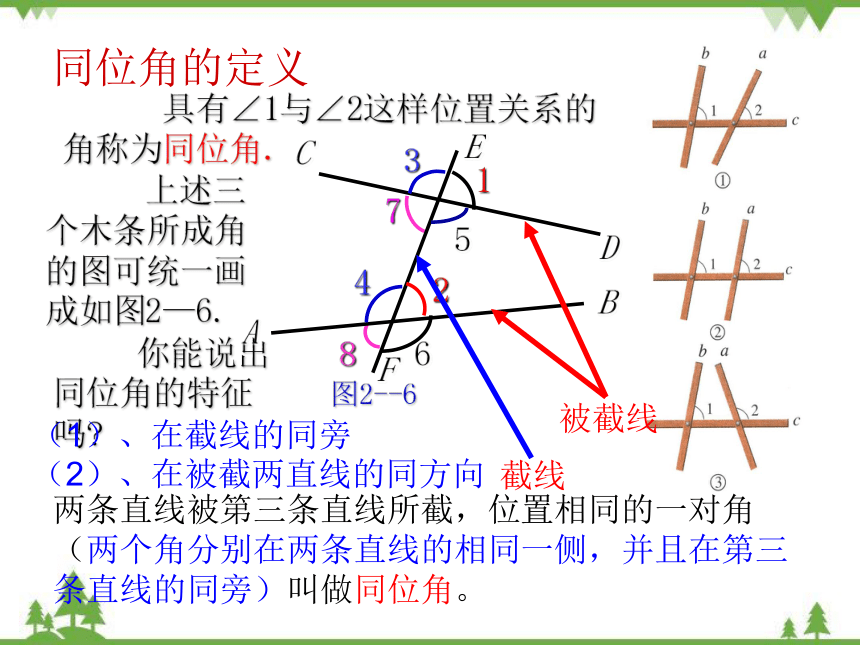
具有∠1与∠2这样位置关系的角称为同位角.
上述三个木条所成角的图可统一画成如图2—6.
你能说出同位角的特征吗
F
1
3
7
5
2
4
8
6
D
C
A
B
E
图2--6
同位角的定义
被截线
截线
(1)、在截线的同旁
(2)、在被截两直线的同方向
两条直线被第三条直线所截,位置相同的一对角(两个角分别在两条直线的相同一侧,并且在第三条直线的同旁)叫做同位角。
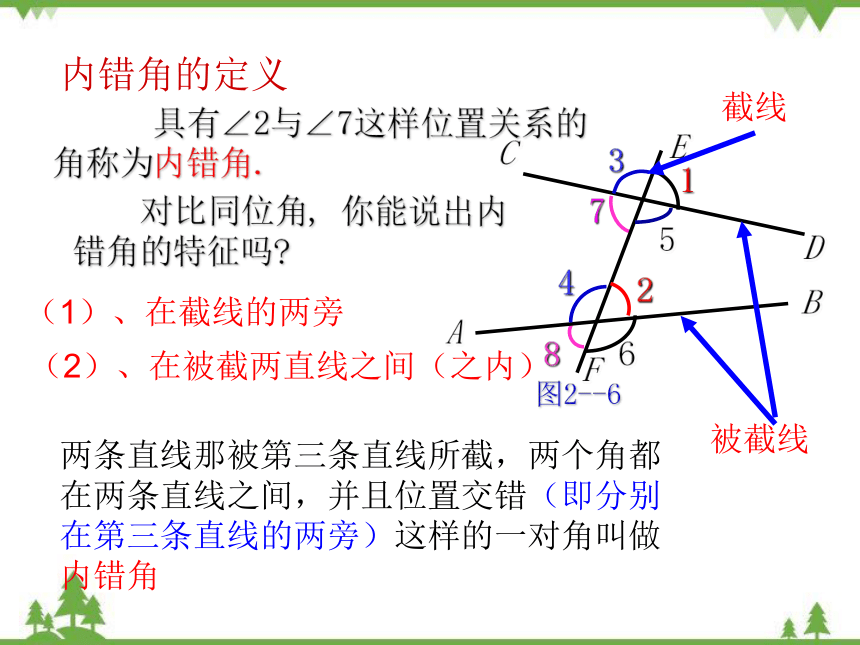
具有∠2与∠7这样位置关系的角称为内错角.
对比同位角, 你能说出内错角的特征吗
F
1
3
7
5
2
4
8
6
D
C
A
B
E
图2--6
内错角的定义
被截线
截线
(1)、在截线的两旁
(2)、在被截两直线之间(之内)
两条直线那被第三条直线所截,两个角都在两条直线之间,并且位置交错(即分别在第三条直线的两旁)这样的一对角叫做内错角
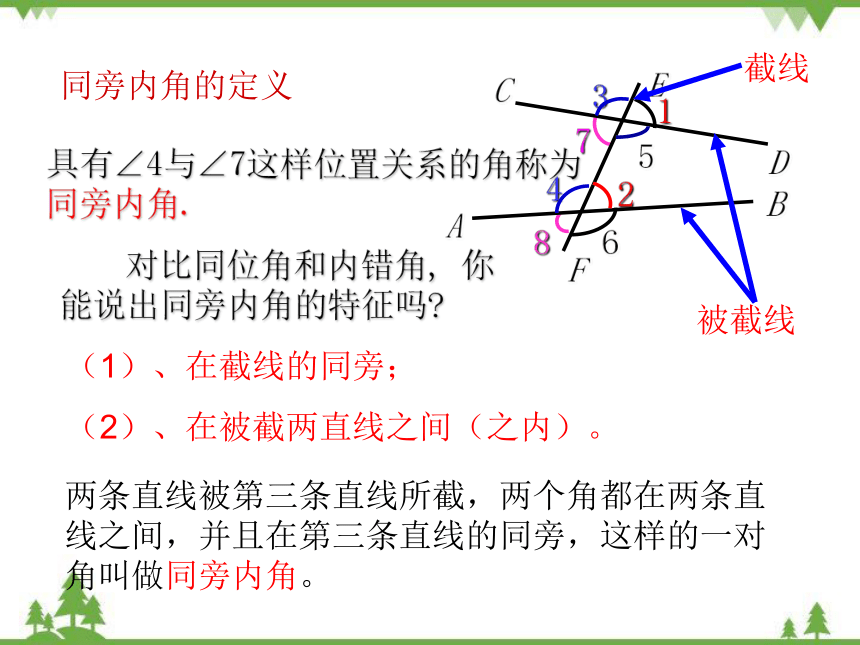
同旁内角的定义
F
1
3
7
5
2
8
6
D
C
A
B
E
4
具有∠4与∠7这样位置关系的角称为同旁内角.
对比同位角和内错角, 你能说出同旁内角的特征吗
被截线
截线
(1)、在截线的同旁;
(2)、在被截两直线之间(之内)。
两条直线被第三条直线所截,两个角都在两条直线之间,并且在第三条直线的同旁,这样的一对角叫做同旁内角。
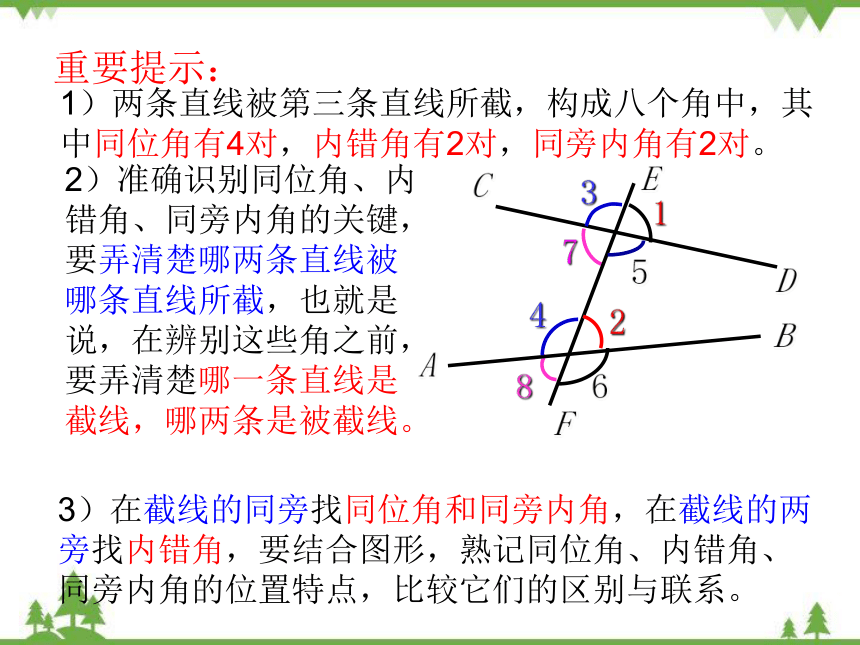
重要提示:
1)两条直线被第三条直线所截,构成八个角中,其中同位角有4对,内错角有2对,同旁内角有2对。
2)准确识别同位角、内错角、同旁内角的关键,要弄清楚哪两条直线被哪条直线所截,也就是说,在辨别这些角之前,要弄清楚哪一条直线是截线,哪两条是被截线。
3)在截线的同旁找同位角和同旁内角,在截线的两旁找内错角,要结合图形,熟记同位角、内错角、同旁内角的位置特点,比较它们的区别与联系。
F
1
3
7
5
2
8
6
D
C
A
B
E
4
同位角(F型)
内错角(Z型或N型)
同旁内角(U型)
归纳总结
练习1
如图,(1)指出DC、AB被AC所截的内错角;
(2)指出AD、BC被AE所截的同位角
答:
∠1与∠5
答:
∠9与∠DAE
练习1
如图(3)∠4与∠7,∠2与∠6,∠9与∠EAD,∠ADC与∠DAB分别是什么关系的角?并指出是哪两条直线被哪一条直线所截的?
答:
∠4与∠7是内错角,是DC、AB被DB所截
∠2与∠6是内错角,是AD、BC被AC所截
∠ADC与∠DAB是同旁内角,是DC、AB被AD所截
∠6与∠7既不是同位角;也不是内错角或同旁内角。
(4)∠6与∠7是什么关系的角?
如图,三根木条相交成∠1,∠2,固定木条b、c,转动木条a , 观察∠1,∠2满足什么条件时直线a与b平行.
当∠1>∠2时
当∠1=∠2时
当∠1<∠2时
①直线a和b不平行
②直线a∥b
③直线a和b不平行
做一做
判断两条直线平行的方法1:
当∠1>∠2时
①直线a和b ,
当∠1=∠2时
②直线a b;
当∠1<∠2时
③直线a和b 。
不平行
∥
不平行
1
2
由此可得:
同位角相等,两直线平行。
∠1、∠2是 角。
同位
两直线平行的判断
你还记得怎样用移动三角尺的方法画两条平行线吗?
同位角相等,两直线平行.
一、放
二、靠
三、推
四、画
0 1 2 3 4 5
0 1 2 3 4 5 6 7 8 9 10
0 1 2 3 4 5 6 7 8 9 10
请说出其中的道理。
0 1 2 3 4 5
0 1 2 3 4 5 6 7 8 9 10
0 1 2 3 4 5 6 7 8 9 10
0 1 2 3 4 5
0 1 2 3 4 5 6 7 8 9 10
0 1 2 3 4 5 6 7 8 9 10
0 1 2 3 4 5
0 1 2 3 4 5 6 7 8 9 10
0 1 2 3 4 5 6 7 8 9 10
0 1 2 3 4 5
0 1 2 3 4 5 6 7 8 9 10
0 1 2 3 4 5 6 7 8 9 10
0 1 2 3 4 5 6 7 8 9 10
0 1 2 3 4 5
0 1 2 3 4 5
●
试用这种方法 过已知直线外一点画它的平行线.
议一议
1、如图,∠1 = ∠2 = 55°, ∠3等于多少度?
直线AB、CD平行吗? 说明你的理由。
3
1
2
A
B
F
C
D
E
∵ ∠1 = ∠2 = 55°
∠3 = ∠2
∴ ∠3 =∠1= 55°
∴ AB∥CD.
随堂练习
( )
对顶角相等
(同位角相等,两直线平行)
小结:
(1)、在截线的同旁
(2)、在被截两直线的同方向
1、同位角的特征(F型)
(1)、在截线的两旁
(2)、在被截两直线之间(之内)
2、内错角的特征(Z型或N型)
(1)、在截线的同旁;
(2)、在被截两直线之间(之内)。
3、同旁内角的特征(U型)
祝同学们学习进步
新人教版-七年级(下)数学-第五章
5 .2.1 直线平行的条件(1)
一、学习目标
1、学会辨别同位角、内错角、同旁内角;
2、掌握“同位角相等,两直线平行”的条件,并能解决一些实际问题;
二、重点和难点
重点:探索两直线平行的条件
难点:同位角的寻找
回顾与思考
在同一平面内
相交
平行
二条直线的位置关系是:
的两条直线叫做平行线.
同一平面内,不相交
同一平面内
根据平行线的定义,两条直线平行必须符合
什么条件
——(1)同一平面内;
(2) 没有交点.
具有∠1与∠2这样位置关系的角称为同位角.
上述三个木条所成角的图可统一画成如图2—6.
你能说出同位角的特征吗
F
1
3
7
5
2
4
8
6
D
C
A
B
E
图2--6
同位角的定义
被截线
截线
(1)、在截线的同旁
(2)、在被截两直线的同方向
两条直线被第三条直线所截,位置相同的一对角(两个角分别在两条直线的相同一侧,并且在第三条直线的同旁)叫做同位角。
具有∠2与∠7这样位置关系的角称为内错角.
对比同位角, 你能说出内错角的特征吗
F
1
3
7
5
2
4
8
6
D
C
A
B
E
图2--6
内错角的定义
被截线
截线
(1)、在截线的两旁
(2)、在被截两直线之间(之内)
两条直线那被第三条直线所截,两个角都在两条直线之间,并且位置交错(即分别在第三条直线的两旁)这样的一对角叫做内错角
同旁内角的定义
F
1
3
7
5
2
8
6
D
C
A
B
E
4
具有∠4与∠7这样位置关系的角称为同旁内角.
对比同位角和内错角, 你能说出同旁内角的特征吗
被截线
截线
(1)、在截线的同旁;
(2)、在被截两直线之间(之内)。
两条直线被第三条直线所截,两个角都在两条直线之间,并且在第三条直线的同旁,这样的一对角叫做同旁内角。
重要提示:
1)两条直线被第三条直线所截,构成八个角中,其中同位角有4对,内错角有2对,同旁内角有2对。
2)准确识别同位角、内错角、同旁内角的关键,要弄清楚哪两条直线被哪条直线所截,也就是说,在辨别这些角之前,要弄清楚哪一条直线是截线,哪两条是被截线。
3)在截线的同旁找同位角和同旁内角,在截线的两旁找内错角,要结合图形,熟记同位角、内错角、同旁内角的位置特点,比较它们的区别与联系。
F
1
3
7
5
2
8
6
D
C
A
B
E
4
同位角(F型)
内错角(Z型或N型)
同旁内角(U型)
归纳总结
练习1
如图,(1)指出DC、AB被AC所截的内错角;
(2)指出AD、BC被AE所截的同位角
答:
∠1与∠5
答:
∠9与∠DAE
练习1
如图(3)∠4与∠7,∠2与∠6,∠9与∠EAD,∠ADC与∠DAB分别是什么关系的角?并指出是哪两条直线被哪一条直线所截的?
答:
∠4与∠7是内错角,是DC、AB被DB所截
∠2与∠6是内错角,是AD、BC被AC所截
∠ADC与∠DAB是同旁内角,是DC、AB被AD所截
∠6与∠7既不是同位角;也不是内错角或同旁内角。
(4)∠6与∠7是什么关系的角?
如图,三根木条相交成∠1,∠2,固定木条b、c,转动木条a , 观察∠1,∠2满足什么条件时直线a与b平行.
当∠1>∠2时
当∠1=∠2时
当∠1<∠2时
①直线a和b不平行
②直线a∥b
③直线a和b不平行
做一做
判断两条直线平行的方法1:
当∠1>∠2时
①直线a和b ,
当∠1=∠2时
②直线a b;
当∠1<∠2时
③直线a和b 。
不平行
∥
不平行
1
2
由此可得:
同位角相等,两直线平行。
∠1、∠2是 角。
同位
两直线平行的判断
你还记得怎样用移动三角尺的方法画两条平行线吗?
同位角相等,两直线平行.
一、放
二、靠
三、推
四、画
0 1 2 3 4 5
0 1 2 3 4 5 6 7 8 9 10
0 1 2 3 4 5 6 7 8 9 10
请说出其中的道理。
0 1 2 3 4 5
0 1 2 3 4 5 6 7 8 9 10
0 1 2 3 4 5 6 7 8 9 10
0 1 2 3 4 5
0 1 2 3 4 5 6 7 8 9 10
0 1 2 3 4 5 6 7 8 9 10
0 1 2 3 4 5
0 1 2 3 4 5 6 7 8 9 10
0 1 2 3 4 5 6 7 8 9 10
0 1 2 3 4 5
0 1 2 3 4 5 6 7 8 9 10
0 1 2 3 4 5 6 7 8 9 10
0 1 2 3 4 5 6 7 8 9 10
0 1 2 3 4 5
0 1 2 3 4 5
●
试用这种方法 过已知直线外一点画它的平行线.
议一议
1、如图,∠1 = ∠2 = 55°, ∠3等于多少度?
直线AB、CD平行吗? 说明你的理由。
3
1
2
A
B
F
C
D
E
∵ ∠1 = ∠2 = 55°
∠3 = ∠2
∴ ∠3 =∠1= 55°
∴ AB∥CD.
随堂练习
( )
对顶角相等
(同位角相等,两直线平行)
小结:
(1)、在截线的同旁
(2)、在被截两直线的同方向
1、同位角的特征(F型)
(1)、在截线的两旁
(2)、在被截两直线之间(之内)
2、内错角的特征(Z型或N型)
(1)、在截线的同旁;
(2)、在被截两直线之间(之内)。
3、同旁内角的特征(U型)
祝同学们学习进步
