2021-2022学年人教版七年级数学下册 5.2.2平行线的判定 同步训练(word版含答案)
文档属性
| 名称 | 2021-2022学年人教版七年级数学下册 5.2.2平行线的判定 同步训练(word版含答案) |

|
|
| 格式 | doc | ||
| 文件大小 | 212.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-12-28 18:49:05 | ||
图片预览

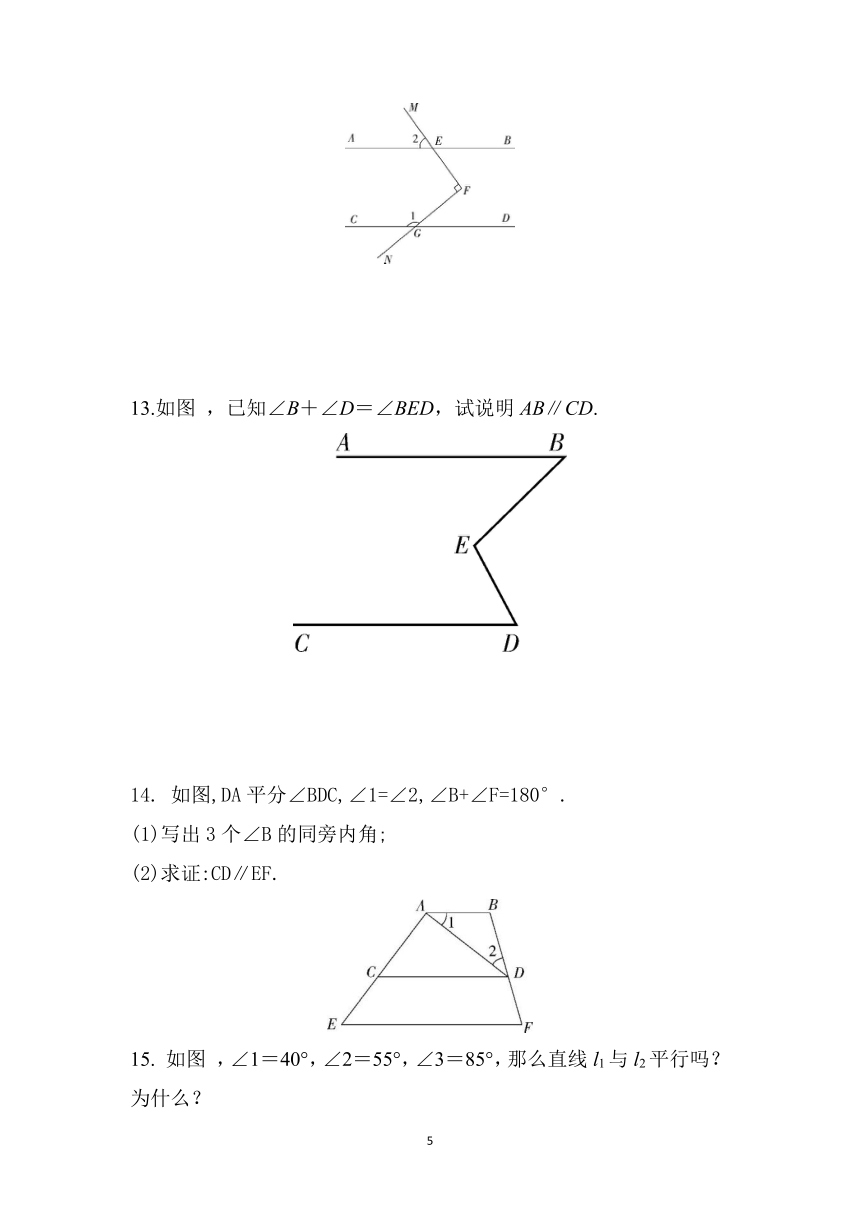
文档简介
2022年春人教版初中七年级数学下册 同步训练
班级 姓名
第五章 相交线与平行线
5.2 平行线及其判定
5.2.2 平行线的判定
一、选择题
1.下列图形中,由∠1=∠2能得到AB∥CD的是( )
2.如图,已知∠2=110°,要使a∥b,则须具备另一个条件,这个条件可以是( )
A.∠3=70° B.∠3=110°
C.∠4=70° D.∠1=70°
3.如图,下列选项中,不能得出直线l1∥l2的是( )
A.∠1=∠2 B.∠4=∠5
C.∠2+∠4=180° D.∠1=∠3
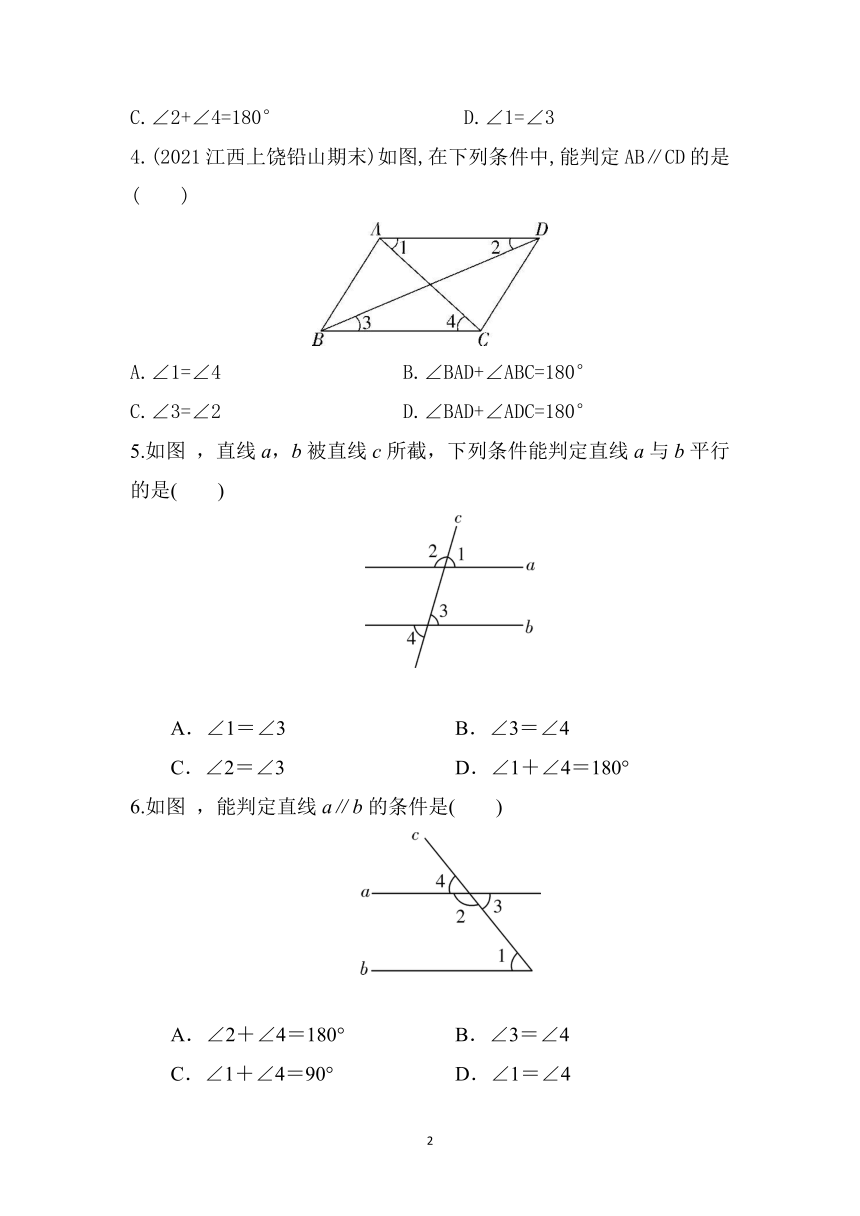
4.(2021江西上饶铅山期末)如图,在下列条件中,能判定AB∥CD的是( )
A.∠1=∠4 B.∠BAD+∠ABC=180°
C.∠3=∠2 D.∠BAD+∠ADC=180°
5.如图 ,直线a,b被直线c所截,下列条件能判定直线a与b平行的是( )
A.∠1=∠3 B.∠3=∠4
C.∠2=∠3 D.∠1+∠4=180°
6.如图 ,能判定直线a∥b的条件是( )
A.∠2+∠4=180° B.∠3=∠4
C.∠1+∠4=90° D.∠1=∠4
二、填空题
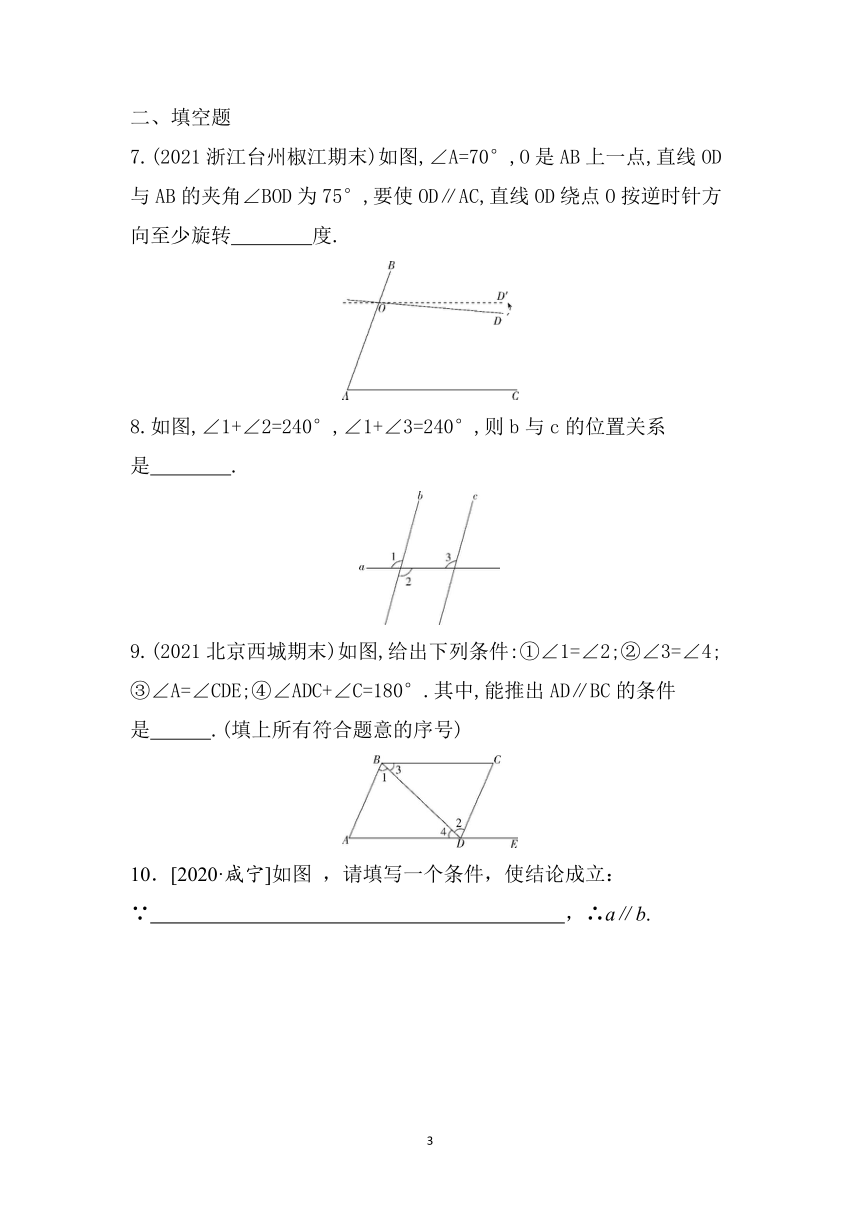
7.(2021浙江台州椒江期末)如图,∠A=70°,O是AB上一点,直线OD与AB的夹角∠BOD为75°,要使OD∥AC,直线OD绕点O按逆时针方向至少旋转 度.
8.如图,∠1+∠2=240°,∠1+∠3=240°,则b与c的位置关系是 .
9.(2021北京西城期末)如图,给出下列条件:①∠1=∠2;②∠3=∠4;③∠A=∠CDE;④∠ADC+∠C=180°.其中,能推出AD∥BC的条件是 .(填上所有符合题意的序号)
10.[2020·咸宁]如图 ,请填写一个条件,使结论成立:
∵ ,∴a∥b.
三、解答题
11.(2021山东济南高新区期末)填写下列空格(推理的理由或数学表达式):
已知:如图,CE平分∠ACD,∠AEC=∠ACE.
求证:AB∥CD.
证明:∵CE平分∠ACD(已知),
∴∠ =∠ ( ).
∵∠AEC=∠ACE(已知),
∴∠AEC=∠ ( ).
∴AB∥CD( ).
12.(2020江西赣州期中)MF⊥NF于F,MF交AB于点E,NF交CD于点G,∠1=140°,∠2=50°,试判断AB和CD的位置关系,并说明理由.
13.如图 ,已知∠B+∠D=∠BED,试说明AB∥CD.
14. 如图,DA平分∠BDC,∠1=∠2,∠B+∠F=180°.
(1)写出3个∠B的同旁内角;
(2)求证:CD∥EF.
15. 如图 ,∠1=40°,∠2=55°,∠3=85°,那么直线l1与l2平行吗?为什么?
一、选择题
1.答案 B A.若∠1+∠2=180°,则AB∥CD,不符合题意;
B.若∠1=∠2,则AB∥CD,符合题意;
C.由∠1=∠2得不出AB∥CD,不符合题意;
D.若∠1=∠2,则AD∥BC,不符合题意.故选B.
2.答案 A 当∠3=70°,∠2=110°时,∠2+∠3=180°,
∴a∥b(同旁内角互补,两直线平行),故选A.
3.答案 A A.由∠1=∠2不能判定直线l1∥l2,故此选项符合题意;
B.根据同位角相等,两直线平行,可判定直线l1∥l2,故此选项不合题意;
C.根据同旁内角互补,两直线平行,可判定直线l1∥l2,故此选项不合题意;
D.根据内错角相等,两直线平行,可判定直线l1∥l2,故此选项不合题意.
故选A.
4.答案 D 由∠1=∠4可判定AD∥BC,不能判定AB∥CD;
由∠BAD+∠ABC=180°可判定AD∥BC,不能判定AB∥CD;
由∠3=∠2可判定AD∥BC,不能判定AB∥CD;
由∠BAD+∠ADC=180°能判定AB∥CD,故选项A、B、C不符合题意,选项D符合题意.
故选D.
5.答案 A
6. 答案 D
二、填空题
7.答案 5
解析 当OD旋转到OD'时,OD'∥AC,根据同位角相等,两直线平行,则需要∠BOD'=∠A=70°.∴∠DOD'=∠BOD-∠BOD'=75°-70°=5°.∴要使OD∥AC,直线OD绕点O按逆时针方向至少旋转5度.故答案为5.
8.答案 b∥c
解析 ∵∠1+∠2=240°,∠1+∠3=240°,∴∠2=∠3,∴b∥c.
9.答案 ②④
解析 ①∵∠1=∠2,∴AB∥CD;
②∵∠3=∠4,∴AD∥BC;
③∵∠A=∠CDE,∴AB∥CD;
④∵∠ADC+∠C=180°,∴AD∥BC.故答案为②④.
10. 答案 ∠1=∠4或∠2=∠4或∠3+∠4=180°
三、解答题
11.解析 证明:∵CE平分∠ACD(已知),
∴∠ACE=∠DCE(角平分线的定义).
∵∠AEC=∠ACE(已知),
∴∠AEC=∠DCE(等量代换).
∴AB∥CD(内错角相等,两直线平行).
12.解析 AB∥CD.理由如下:
如图,延长MF交CD于点H,
∵∠1=140°,∴∠FGH=40°,
∵MF⊥NF,∴∠GFH=90°,
∴∠CHF=180°-40°-90°=50°,
∴∠CHF=∠2,∴AB∥CD.
13.解:如答图,过点E作∠BEF=∠B,
则有AB∥EF.
∵∠BED=∠BEF+∠DEF,
∠BED=∠B+∠D,
∴∠DEF=∠D,
∴CD∥EF.
又∵AB∥EF,
∴AB∥CD.
14.解析 (1)答案不唯一,∠B的同旁内角有∠2、∠BDC、∠F.
(2)证明:∵DA平分∠BDC,
∴∠ADC=∠2=∠BDC,
∵∠1=∠2,∴∠1=∠ADC,
∴AB∥CD,
∵∠B+∠F=180°,∴AB∥EF,
∴EF∥CD.
15.解:l1∥l2.理由如下:
∵∠2=55°,∴∠4=∠2=55°.
又∵∠3=85°,
∴∠5=180°-∠3-∠4=180°-85°-55°=40°.
又∵∠1=40°,∴∠1=∠5,∴l1∥l2.
1
班级 姓名
第五章 相交线与平行线
5.2 平行线及其判定
5.2.2 平行线的判定
一、选择题
1.下列图形中,由∠1=∠2能得到AB∥CD的是( )
2.如图,已知∠2=110°,要使a∥b,则须具备另一个条件,这个条件可以是( )
A.∠3=70° B.∠3=110°
C.∠4=70° D.∠1=70°
3.如图,下列选项中,不能得出直线l1∥l2的是( )
A.∠1=∠2 B.∠4=∠5
C.∠2+∠4=180° D.∠1=∠3
4.(2021江西上饶铅山期末)如图,在下列条件中,能判定AB∥CD的是( )
A.∠1=∠4 B.∠BAD+∠ABC=180°
C.∠3=∠2 D.∠BAD+∠ADC=180°
5.如图 ,直线a,b被直线c所截,下列条件能判定直线a与b平行的是( )
A.∠1=∠3 B.∠3=∠4
C.∠2=∠3 D.∠1+∠4=180°
6.如图 ,能判定直线a∥b的条件是( )
A.∠2+∠4=180° B.∠3=∠4
C.∠1+∠4=90° D.∠1=∠4
二、填空题
7.(2021浙江台州椒江期末)如图,∠A=70°,O是AB上一点,直线OD与AB的夹角∠BOD为75°,要使OD∥AC,直线OD绕点O按逆时针方向至少旋转 度.
8.如图,∠1+∠2=240°,∠1+∠3=240°,则b与c的位置关系是 .
9.(2021北京西城期末)如图,给出下列条件:①∠1=∠2;②∠3=∠4;③∠A=∠CDE;④∠ADC+∠C=180°.其中,能推出AD∥BC的条件是 .(填上所有符合题意的序号)
10.[2020·咸宁]如图 ,请填写一个条件,使结论成立:
∵ ,∴a∥b.
三、解答题
11.(2021山东济南高新区期末)填写下列空格(推理的理由或数学表达式):
已知:如图,CE平分∠ACD,∠AEC=∠ACE.
求证:AB∥CD.
证明:∵CE平分∠ACD(已知),
∴∠ =∠ ( ).
∵∠AEC=∠ACE(已知),
∴∠AEC=∠ ( ).
∴AB∥CD( ).
12.(2020江西赣州期中)MF⊥NF于F,MF交AB于点E,NF交CD于点G,∠1=140°,∠2=50°,试判断AB和CD的位置关系,并说明理由.
13.如图 ,已知∠B+∠D=∠BED,试说明AB∥CD.
14. 如图,DA平分∠BDC,∠1=∠2,∠B+∠F=180°.
(1)写出3个∠B的同旁内角;
(2)求证:CD∥EF.
15. 如图 ,∠1=40°,∠2=55°,∠3=85°,那么直线l1与l2平行吗?为什么?
一、选择题
1.答案 B A.若∠1+∠2=180°,则AB∥CD,不符合题意;
B.若∠1=∠2,则AB∥CD,符合题意;
C.由∠1=∠2得不出AB∥CD,不符合题意;
D.若∠1=∠2,则AD∥BC,不符合题意.故选B.
2.答案 A 当∠3=70°,∠2=110°时,∠2+∠3=180°,
∴a∥b(同旁内角互补,两直线平行),故选A.
3.答案 A A.由∠1=∠2不能判定直线l1∥l2,故此选项符合题意;
B.根据同位角相等,两直线平行,可判定直线l1∥l2,故此选项不合题意;
C.根据同旁内角互补,两直线平行,可判定直线l1∥l2,故此选项不合题意;
D.根据内错角相等,两直线平行,可判定直线l1∥l2,故此选项不合题意.
故选A.
4.答案 D 由∠1=∠4可判定AD∥BC,不能判定AB∥CD;
由∠BAD+∠ABC=180°可判定AD∥BC,不能判定AB∥CD;
由∠3=∠2可判定AD∥BC,不能判定AB∥CD;
由∠BAD+∠ADC=180°能判定AB∥CD,故选项A、B、C不符合题意,选项D符合题意.
故选D.
5.答案 A
6. 答案 D
二、填空题
7.答案 5
解析 当OD旋转到OD'时,OD'∥AC,根据同位角相等,两直线平行,则需要∠BOD'=∠A=70°.∴∠DOD'=∠BOD-∠BOD'=75°-70°=5°.∴要使OD∥AC,直线OD绕点O按逆时针方向至少旋转5度.故答案为5.
8.答案 b∥c
解析 ∵∠1+∠2=240°,∠1+∠3=240°,∴∠2=∠3,∴b∥c.
9.答案 ②④
解析 ①∵∠1=∠2,∴AB∥CD;
②∵∠3=∠4,∴AD∥BC;
③∵∠A=∠CDE,∴AB∥CD;
④∵∠ADC+∠C=180°,∴AD∥BC.故答案为②④.
10. 答案 ∠1=∠4或∠2=∠4或∠3+∠4=180°
三、解答题
11.解析 证明:∵CE平分∠ACD(已知),
∴∠ACE=∠DCE(角平分线的定义).
∵∠AEC=∠ACE(已知),
∴∠AEC=∠DCE(等量代换).
∴AB∥CD(内错角相等,两直线平行).
12.解析 AB∥CD.理由如下:
如图,延长MF交CD于点H,
∵∠1=140°,∴∠FGH=40°,
∵MF⊥NF,∴∠GFH=90°,
∴∠CHF=180°-40°-90°=50°,
∴∠CHF=∠2,∴AB∥CD.
13.解:如答图,过点E作∠BEF=∠B,
则有AB∥EF.
∵∠BED=∠BEF+∠DEF,
∠BED=∠B+∠D,
∴∠DEF=∠D,
∴CD∥EF.
又∵AB∥EF,
∴AB∥CD.
14.解析 (1)答案不唯一,∠B的同旁内角有∠2、∠BDC、∠F.
(2)证明:∵DA平分∠BDC,
∴∠ADC=∠2=∠BDC,
∵∠1=∠2,∴∠1=∠ADC,
∴AB∥CD,
∵∠B+∠F=180°,∴AB∥EF,
∴EF∥CD.
15.解:l1∥l2.理由如下:
∵∠2=55°,∴∠4=∠2=55°.
又∵∠3=85°,
∴∠5=180°-∠3-∠4=180°-85°-55°=40°.
又∵∠1=40°,∴∠1=∠5,∴l1∥l2.
1
