华东师大版八年级数学下册19.2.1第2课时菱形性质的应用 同步练习(word版含答案)
文档属性
| 名称 | 华东师大版八年级数学下册19.2.1第2课时菱形性质的应用 同步练习(word版含答案) |
|
|
| 格式 | docx | ||
| 文件大小 | 150.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-12-28 00:00:00 | ||
图片预览




文档简介
19.2.1第2课时 菱形性质的应用
一、选择题
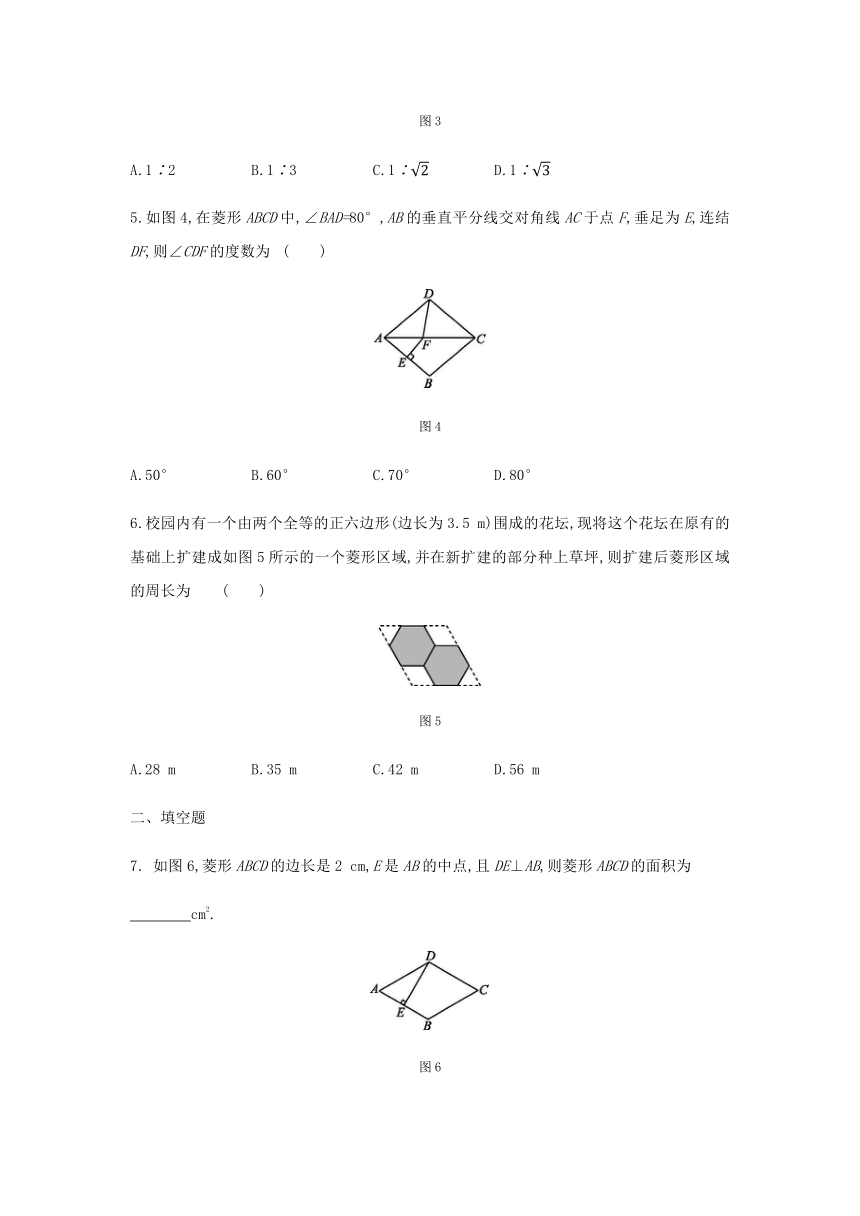
1.如图1,某菱形花坛ABCD的周长是24 m,∠BAD=120°,则花坛的对角线AC的长是 ( )
图1
A. m B.6 m C. m D.3 m
2.如图2,已知四边形ABCD是菱形,CE⊥AB交AB的延长线于点E,CF⊥AD交AD的延长线于点F.若CF=3,则CE的长为 ( )
图2
A.5 B.4 C.3 D.2
3.已知一个菱形的周长是20 cm,两条对角线的长度之比是4∶3,则这个菱形的面积是( )
A.12 cm2 B.24 cm2
C.48 cm2 D.96 cm2
4.如图3,菱形ABCD的周长为8 cm,BC边上的高AE为 cm,则对角线AC和BD的长度之比为 ( )
图3
A.1∶2 B.1∶3 C.1∶ D.1∶
5.如图4,在菱形ABCD中,∠BAD=80°,AB的垂直平分线交对角线AC于点F,垂足为E,连结DF,则∠CDF的度数为 ( )
图4
A.50° B.60° C.70° D.80°
6.校园内有一个由两个全等的正六边形(边长为3.5 m)围成的花坛,现将这个花坛在原有的基础上扩建成如图5所示的一个菱形区域,并在新扩建的部分种上草坪,则扩建后菱形区域的周长为 ( )
图5
A.28 m B.35 m C.42 m D.56 m
二、填空题
7. 如图6,菱形ABCD的边长是2 cm,E是AB的中点,且DE⊥AB,则菱形ABCD的面积为
cm2.
图6
8.如图7,菱形ABCD的对角线AC,BD相交于点O,且AC=8,BD=6,过点O作OH⊥AB,垂足为H,则点O到边AB的距离OH= .
图7
9.如图8所示,菱形ABCD的对角线的长分别为3和6,P是对角线AC上任一点(点P不与点A,C重合),且PE∥BC交AB于点E,PF∥CD交AD于点F,则阴影部分的面积是 .
图8
10.如图9,用3个全等的菱形构成活动衣帽架,顶点A,E,F,C,G,H是上、下两排挂钩,根据需要可以改变挂钩之间的距离(比如A,C两点可以自由上下活动).若菱形的边长为13厘米,要使两排挂钩之间的距离为24厘米,并在点B,M处固定,则点B,M之间的距离是 .
图9
三、解答题
11.如图10,在菱形ABCD中,P是BC边上的一点,连结AP,E,F是AP上的两点,连结DE,BF,使得∠AED=∠ABC,∠ABF=∠BPF.
求证:(1)△ABF≌△DAE;
(2)DE=BF+EF.
图10
12.如图11所示,在菱形ABCD中,P是AB上的一个动点(不与点A,B重合),连结DP,交对角线AC于点E,连结BE.
(1)求证:∠APD=∠CBE;
(2)当点P运动到什么位置时,△ADP的面积等于菱形ABCD面积的 为什么
图11
13.在菱形ABCD中,∠B=60°,点E在边BC上,点F在边CD上.
(1)如图12①,若E是BC的中点,∠AEF=60°,求证:BE=DF;
(2)如图②,若∠EAF=60°,求证:△AEF是等边三角形.
图12
14.如图,在菱形ABCD中,AB=2,E为BC边的中点,G为AD边上的一点,四边形AECG是矩形,AF⊥CD,垂足为F,CG与AF相交于点H.
(1)求菱形ABCD的面积;
(2)求∠CHA的度数.
15.已知:如图,在菱形ABCD中,∠B=60°,E,F分别是AB,AD上的两个动点,且始终保持∠ECF=60°.
(1)试判断△ECF的形状,并说明理由;
(2)若菱形的边长为2 cm,求CE的最小值.
答案
1.B
2.C .
3.B
4.D
5.B
6.C
7.2
8.
9.
10.30厘米
11.证明:(1)∵四边形ABCD是菱形,
∴AB=DA,DA∥BC,
∴∠BPA=∠EAD.
又∵∠ABC=∠AED,
∴∠BAF=∠ADE.
∵∠ABF=∠BPF且∠BAP=∠FAB,
∴∠ABP=∠BFA,
∴∠BFA=∠AED.
又∵AB=DA,∠BAF=∠ADE,
∴△ABF≌△DAE.
(2)∵△ABF≌△DAE,
∴BF=AE,AF=DE.
∵AF=AE+EF=BF+EF,
∴DE=BF+EF.
12.解:(1)证明:∵菱形ABCD是以对角线AC所在直线为对称轴的轴对称图形,
且点C与点C对应,点D与点B对应,点E与点E对应,
∴△CDE与△CBE关于直线AC对称,
∴∠CBE=∠CDE.
又∵AB∥DC,∴∠APD=∠CDE,
∴∠APD=∠CBE.
(2)当点P运动到AB边的中点时,△ADP的面积等于菱形ABCD面积的.
理由:如图,连结DB,
则S△ABD=S菱形ABCD.
∵P为AB边的中点,
∴S△ADP=S△ABD,
∴S△ADP=S菱形ABCD.
13.证明:(1)连结AC.
∵四边形ABCD是菱形,∴AB=BC=CD.
又∵∠B=60°,∴△ABC是等边三角形.
∵E是BC的中点,∴AE⊥BC.
∵∠AEF=60°,∴∠FEC=90°-60°=30°.
∵∠BCD=180°-∠B=120°,∴∠EFC=30°,
∴∠FEC=∠EFC,∴CE=CF.
又∵BC=CD,
∴BC-CE=CD-CF,即BE=DF.
(2)连结AC,由(1)得△ABC是等边三角形,
∴AB=AC,∠BAC=∠ACB=60°,
∴∠BAE+∠EAC=60°.
又∵∠EAF=∠CAF+∠EAC=60°,
∴∠BAE=∠CAF.
∵∠BCD=120°,∠ACB=60°,
∴∠ACF=60°=∠B,
∴△ABE≌△ACF,∴AE=AF.
又∵∠EAF=60°,
∴△AEF是等边三角形.
14.解:(1)∵在菱形ABCD中,AB=BC=2,E为BC边的中点,
∴BE=1.
∵四边形AECG为矩形,∴∠AEC=90°,
∴∠AEB=90°.
在Rt△ABE中,AE==,
∴菱形ABCD的面积=BC·AE=2.
(2)连结AC.
∵E为BC边的中点,AE⊥BC,
∴AB=AC.
又∵AB=BC,
∴△ABC为等边三角形,∴∠B=60°,
∴∠D=∠B=60°.
∵AF⊥CD,∴∠DAF=30°.
在矩形AECG中,∠AGH=90°,
∴∠CHA=∠DAF+∠AGH=30°+90°=120°.
15.解:(1)△ECF是等边三角形.
理由:连结AC.
∵四边形ABCD是菱形,
∴AB=BC,AD∥BC.
∵∠B=60°,
∴△ABC是等边三角形,
∴AB=AC=BC,∠ACB=∠BAC=60°,
∴∠FAC=∠ACB=60°=∠B,
∠BCE+∠ACE=60°.
∵∠ECF=60°,∴∠ACE+∠ACF=60°,
∴∠BCE=∠ACF.
在△BCE与△ACF中,
∵∠B=∠FAC,BC=AC,∠BCE=∠ACF,
∴△BCE≌△ACF,
∴CE=CF.
又∵∠ECF=60°,
∴△ECF是等边三角形.
(2)∵垂线段最短,
∴当CE⊥AB时,CE的值最小.
∵△ABC是等边三角形,
∴BE=AE=AB=1 cm,
∴CE===(cm),
∴CE的最小值为 cm.
一、选择题
1.如图1,某菱形花坛ABCD的周长是24 m,∠BAD=120°,则花坛的对角线AC的长是 ( )
图1
A. m B.6 m C. m D.3 m
2.如图2,已知四边形ABCD是菱形,CE⊥AB交AB的延长线于点E,CF⊥AD交AD的延长线于点F.若CF=3,则CE的长为 ( )
图2
A.5 B.4 C.3 D.2
3.已知一个菱形的周长是20 cm,两条对角线的长度之比是4∶3,则这个菱形的面积是( )
A.12 cm2 B.24 cm2
C.48 cm2 D.96 cm2
4.如图3,菱形ABCD的周长为8 cm,BC边上的高AE为 cm,则对角线AC和BD的长度之比为 ( )
图3
A.1∶2 B.1∶3 C.1∶ D.1∶
5.如图4,在菱形ABCD中,∠BAD=80°,AB的垂直平分线交对角线AC于点F,垂足为E,连结DF,则∠CDF的度数为 ( )
图4
A.50° B.60° C.70° D.80°
6.校园内有一个由两个全等的正六边形(边长为3.5 m)围成的花坛,现将这个花坛在原有的基础上扩建成如图5所示的一个菱形区域,并在新扩建的部分种上草坪,则扩建后菱形区域的周长为 ( )
图5
A.28 m B.35 m C.42 m D.56 m
二、填空题
7. 如图6,菱形ABCD的边长是2 cm,E是AB的中点,且DE⊥AB,则菱形ABCD的面积为
cm2.
图6
8.如图7,菱形ABCD的对角线AC,BD相交于点O,且AC=8,BD=6,过点O作OH⊥AB,垂足为H,则点O到边AB的距离OH= .
图7
9.如图8所示,菱形ABCD的对角线的长分别为3和6,P是对角线AC上任一点(点P不与点A,C重合),且PE∥BC交AB于点E,PF∥CD交AD于点F,则阴影部分的面积是 .
图8
10.如图9,用3个全等的菱形构成活动衣帽架,顶点A,E,F,C,G,H是上、下两排挂钩,根据需要可以改变挂钩之间的距离(比如A,C两点可以自由上下活动).若菱形的边长为13厘米,要使两排挂钩之间的距离为24厘米,并在点B,M处固定,则点B,M之间的距离是 .
图9
三、解答题
11.如图10,在菱形ABCD中,P是BC边上的一点,连结AP,E,F是AP上的两点,连结DE,BF,使得∠AED=∠ABC,∠ABF=∠BPF.
求证:(1)△ABF≌△DAE;
(2)DE=BF+EF.
图10
12.如图11所示,在菱形ABCD中,P是AB上的一个动点(不与点A,B重合),连结DP,交对角线AC于点E,连结BE.
(1)求证:∠APD=∠CBE;
(2)当点P运动到什么位置时,△ADP的面积等于菱形ABCD面积的 为什么
图11
13.在菱形ABCD中,∠B=60°,点E在边BC上,点F在边CD上.
(1)如图12①,若E是BC的中点,∠AEF=60°,求证:BE=DF;
(2)如图②,若∠EAF=60°,求证:△AEF是等边三角形.
图12
14.如图,在菱形ABCD中,AB=2,E为BC边的中点,G为AD边上的一点,四边形AECG是矩形,AF⊥CD,垂足为F,CG与AF相交于点H.
(1)求菱形ABCD的面积;
(2)求∠CHA的度数.
15.已知:如图,在菱形ABCD中,∠B=60°,E,F分别是AB,AD上的两个动点,且始终保持∠ECF=60°.
(1)试判断△ECF的形状,并说明理由;
(2)若菱形的边长为2 cm,求CE的最小值.
答案
1.B
2.C .
3.B
4.D
5.B
6.C
7.2
8.
9.
10.30厘米
11.证明:(1)∵四边形ABCD是菱形,
∴AB=DA,DA∥BC,
∴∠BPA=∠EAD.
又∵∠ABC=∠AED,
∴∠BAF=∠ADE.
∵∠ABF=∠BPF且∠BAP=∠FAB,
∴∠ABP=∠BFA,
∴∠BFA=∠AED.
又∵AB=DA,∠BAF=∠ADE,
∴△ABF≌△DAE.
(2)∵△ABF≌△DAE,
∴BF=AE,AF=DE.
∵AF=AE+EF=BF+EF,
∴DE=BF+EF.
12.解:(1)证明:∵菱形ABCD是以对角线AC所在直线为对称轴的轴对称图形,
且点C与点C对应,点D与点B对应,点E与点E对应,
∴△CDE与△CBE关于直线AC对称,
∴∠CBE=∠CDE.
又∵AB∥DC,∴∠APD=∠CDE,
∴∠APD=∠CBE.
(2)当点P运动到AB边的中点时,△ADP的面积等于菱形ABCD面积的.
理由:如图,连结DB,
则S△ABD=S菱形ABCD.
∵P为AB边的中点,
∴S△ADP=S△ABD,
∴S△ADP=S菱形ABCD.
13.证明:(1)连结AC.
∵四边形ABCD是菱形,∴AB=BC=CD.
又∵∠B=60°,∴△ABC是等边三角形.
∵E是BC的中点,∴AE⊥BC.
∵∠AEF=60°,∴∠FEC=90°-60°=30°.
∵∠BCD=180°-∠B=120°,∴∠EFC=30°,
∴∠FEC=∠EFC,∴CE=CF.
又∵BC=CD,
∴BC-CE=CD-CF,即BE=DF.
(2)连结AC,由(1)得△ABC是等边三角形,
∴AB=AC,∠BAC=∠ACB=60°,
∴∠BAE+∠EAC=60°.
又∵∠EAF=∠CAF+∠EAC=60°,
∴∠BAE=∠CAF.
∵∠BCD=120°,∠ACB=60°,
∴∠ACF=60°=∠B,
∴△ABE≌△ACF,∴AE=AF.
又∵∠EAF=60°,
∴△AEF是等边三角形.
14.解:(1)∵在菱形ABCD中,AB=BC=2,E为BC边的中点,
∴BE=1.
∵四边形AECG为矩形,∴∠AEC=90°,
∴∠AEB=90°.
在Rt△ABE中,AE==,
∴菱形ABCD的面积=BC·AE=2.
(2)连结AC.
∵E为BC边的中点,AE⊥BC,
∴AB=AC.
又∵AB=BC,
∴△ABC为等边三角形,∴∠B=60°,
∴∠D=∠B=60°.
∵AF⊥CD,∴∠DAF=30°.
在矩形AECG中,∠AGH=90°,
∴∠CHA=∠DAF+∠AGH=30°+90°=120°.
15.解:(1)△ECF是等边三角形.
理由:连结AC.
∵四边形ABCD是菱形,
∴AB=BC,AD∥BC.
∵∠B=60°,
∴△ABC是等边三角形,
∴AB=AC=BC,∠ACB=∠BAC=60°,
∴∠FAC=∠ACB=60°=∠B,
∠BCE+∠ACE=60°.
∵∠ECF=60°,∴∠ACE+∠ACF=60°,
∴∠BCE=∠ACF.
在△BCE与△ACF中,
∵∠B=∠FAC,BC=AC,∠BCE=∠ACF,
∴△BCE≌△ACF,
∴CE=CF.
又∵∠ECF=60°,
∴△ECF是等边三角形.
(2)∵垂线段最短,
∴当CE⊥AB时,CE的值最小.
∵△ABC是等边三角形,
∴BE=AE=AB=1 cm,
∴CE===(cm),
∴CE的最小值为 cm.
