2021-2022学年人教版初中数学七年级下册 5.1.1相交线 课件(共21张PPT)
文档属性
| 名称 | 2021-2022学年人教版初中数学七年级下册 5.1.1相交线 课件(共21张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 990.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-12-28 00:00:00 | ||
图片预览




文档简介
(共21张PPT)
5.1.1相交线
请找一找图中的相交线
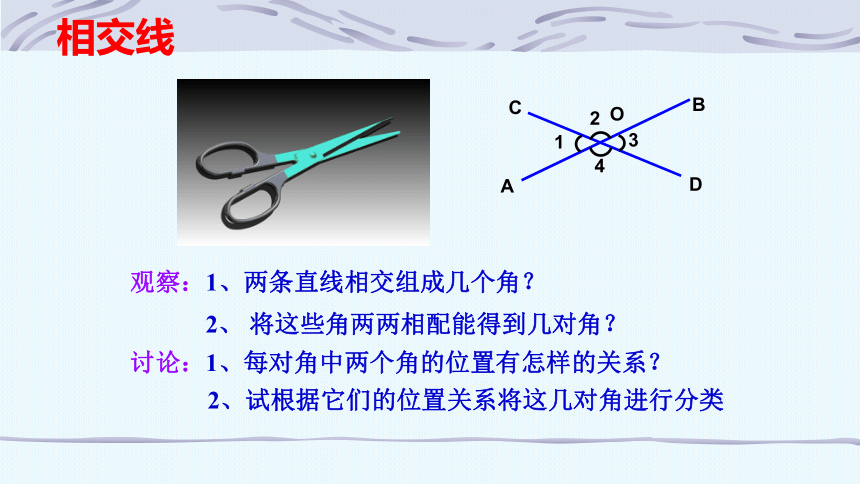
相交线
观察:1、两条直线相交组成几个角?
讨论:1、每对角中两个角的位置有怎样的关系?
2、 将这些角两两相配能得到几对角?
2、试根据它们的位置关系将这几对角进行分类
B
A
C
D
O
1
2
3
4
B
A
C
D
O
1
2
3
4
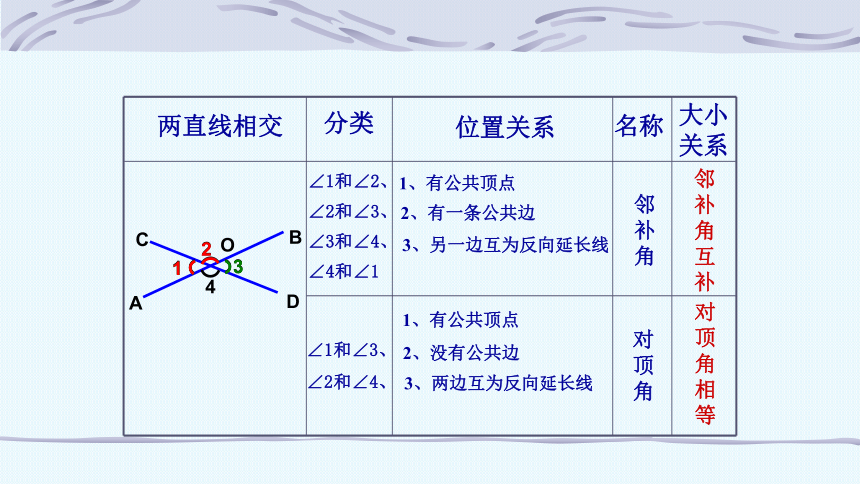
1、有公共顶点
分类
∠1和∠2、∠2和∠3、∠3和∠4、∠4和∠1
∠1和∠3、
∠2和∠4、
1、有公共顶点
位置关系
邻补角
对顶角
2、有一条公共边
3、另一边互为反向延长线
2、没有公共边
两直线相交
3、两边互为反向延长线
名称
1
2
1
3
O
A
B
C
D
)
(
1
3
4
2
)
(
O
A
B
C
D
)
(
1
3
4
2
)
(
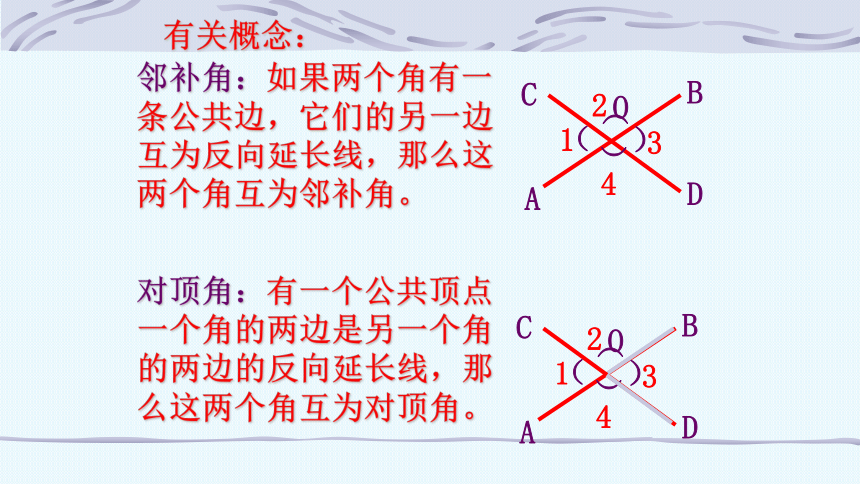
有关概念:
邻补角:如果两个角有一条公共边,它们的另一边互为反向延长线,那么这两个角互为邻补角。
对顶角:有一个公共顶点一个角的两边是另一个角的两边的反向延长线,那么这两个角互为对顶角。
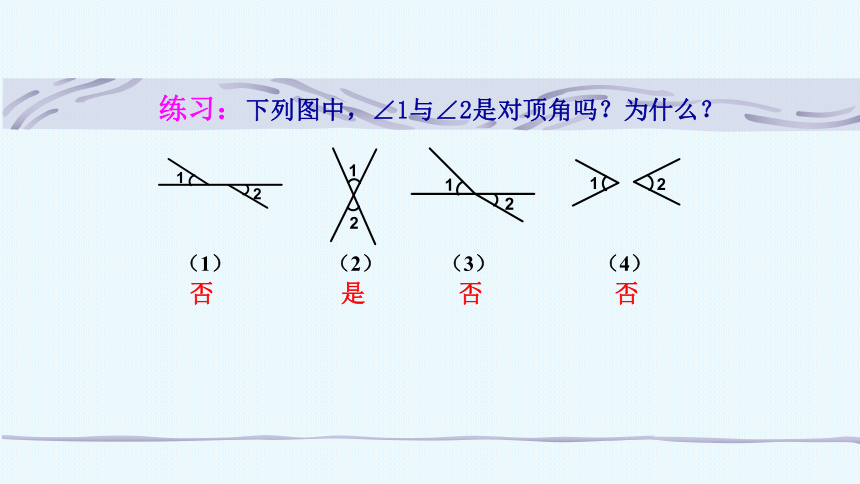
练习:下列图中,∠1与∠2是对顶角吗?为什么?
否
是
否
否
(1)
(2)
(3)
(4)
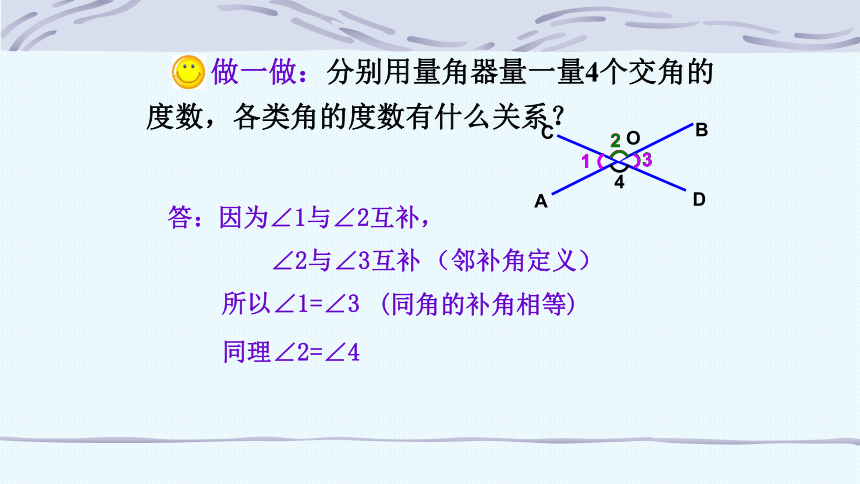
做一做:分别用量角器量一量4个交角的度数,各类角的度数有什么关系?
B
A
C
D
O
1
2
3
4
所以∠1=∠3
同理∠2=∠4
∠2与∠3互补
答:因为∠1与∠2互补,
(邻补角定义)
(同角的补角相等)
1
2
2
3
1
3
1、有公共顶点
分类
∠1和∠2、∠2和∠3、∠3和∠4、∠4和∠1
∠1和∠3、
∠2和∠4、
1、有公共顶点
位置关系
邻补角
对顶角
邻补角互补
2、有一条公共边
3、另一边互为反向延长线
2、没有公共边
两直线相交
3、两边互为反向延长线
名称
大小关系
对顶角相等
B
A
C
D
O
1
2
3
4
1
3
1
2
1、若∠1与∠2是对顶角,∠1=160,则∠2=______0;
若 ∠3与∠4是邻补角,则∠3+∠4 =______0
180
180
2、若∠1与∠2为对顶角,∠1与∠3互补,则 ∠2+∠3= 0
16
跟踪练习:
3.如图,点A,O,B在同一直线上,已知∠BOC=50°,
则∠AOC= °.
130
4.如图,直线AB和CD相交于点O,OE平分∠DOB,
∠AOC=40°,则∠DOE= .
20°
5.如图,已知直线AB,CD相交于点O,且∠EOD=∠DOB,
OF平分∠AOE,若∠AOC=28°,则∠EOF= .
62°
例1:如图,直线a、b相交。
(1) ∠ 1=400, 求∠2,∠3,∠4的度数。
(2) ∠1:∠2=2:7 ,求各角的度数。
∠2=180°-∠1
=180°- 40°
解:(1)由邻补角的定义,可得
=140°
由对顶角相等,可得
∠3=∠1=40°
∠4=∠2=140°
例题分析
2、如图,已知直线AB,CD相交于点O,OA平分∠EOC,∠EOC=700,求∠BOD,∠BOC的度数。
解:因为OA平分∠EOC,∠EOC= 700
所以∠AOC=350
由对顶角相等,得
由邻补角定义,得
∠BOC= 180°-∠AOC
= 180°- 35°
= 145°
∠BOD=∠AOC=350
1、如图1,三条直线AB、CD、
EF两两相交,在这个图形中,有
对顶角_____对,邻补角____ 对.
6
12
∠AOD
∠BOD
∠AOD
∠COE
∠3、
2、如图2,直线AB、CD
相交于O,OE是射线。则
∠3的对顶角是_____________,
∠1的对顶角是_____________,
∠1的邻补角是_____________,
∠2的邻补角是_____________。
课堂练习:
图1
图2
4、已知两条直线相交成的四个角,其中一个角是900,其余各角是_____ 。
900
850
5、如图4,三条直线a,b,c相交于点O,∠1=400,∠2=550,则∠3=_____.
3、如图3,∠2与∠3为邻补角,∠1=∠2,则∠1与∠3的关系为 。
互补
图3
图4
6.下列命题中,正确的是( )
A.有公共顶点,且方向相反的两个角是对顶角
B.有公共点,且又相等的角是对顶角
C.两条直线相交所成的角是对顶角
D.角的两边互为反向延长线的两个角是对顶角
D
7.下列图形中,∠1与∠2是对顶角的是( C )
1.如图是一个对顶角量角器,
你能说明它度量角度的原理吗?
拓展练习
拓展练习
2.找出图中∠AOE的对顶角及邻补角,
若没有请画出.
角的名称
邻补角
对顶角
位置关系
2、有一条公共边
3、另一边互为反向延长线4 .两条直线相交形成的角
1、有公共顶点
1、有公共顶点
2、没有公共边
3、两边互为反向延长线4. 两条直线相交而成;
性质
邻补角互补
对顶角相等
相同点
①都是两条直线相交而成的角; ②都有一个公共顶点;③都是成对出现的
不同点
1. 对 顶角没有公共边而邻补角有一条公共边;
2.两条直线相交时,一个角的对顶角只有一个,而一个角的邻补角有两个.
对顶角有两对,
邻补角有四对
知识回顾:
课堂小结
(1)对顶角与邻补角的概念
(2)能从图中辨认对顶角与邻补角.
(3)知道“对顶角相等”.
(4)了解“对顶角相等”的说理过程.
思考题:
两条直线相交于一点,有几对对顶角?
三条直线相交于一点,有几对对顶角?
四条直线相交于一点,有几对对顶角?
n 条直线相交于一点,有几对对顶角?
5.1.1相交线
请找一找图中的相交线
相交线
观察:1、两条直线相交组成几个角?
讨论:1、每对角中两个角的位置有怎样的关系?
2、 将这些角两两相配能得到几对角?
2、试根据它们的位置关系将这几对角进行分类
B
A
C
D
O
1
2
3
4
B
A
C
D
O
1
2
3
4
1、有公共顶点
分类
∠1和∠2、∠2和∠3、∠3和∠4、∠4和∠1
∠1和∠3、
∠2和∠4、
1、有公共顶点
位置关系
邻补角
对顶角
2、有一条公共边
3、另一边互为反向延长线
2、没有公共边
两直线相交
3、两边互为反向延长线
名称
1
2
1
3
O
A
B
C
D
)
(
1
3
4
2
)
(
O
A
B
C
D
)
(
1
3
4
2
)
(
有关概念:
邻补角:如果两个角有一条公共边,它们的另一边互为反向延长线,那么这两个角互为邻补角。
对顶角:有一个公共顶点一个角的两边是另一个角的两边的反向延长线,那么这两个角互为对顶角。
练习:下列图中,∠1与∠2是对顶角吗?为什么?
否
是
否
否
(1)
(2)
(3)
(4)
做一做:分别用量角器量一量4个交角的度数,各类角的度数有什么关系?
B
A
C
D
O
1
2
3
4
所以∠1=∠3
同理∠2=∠4
∠2与∠3互补
答:因为∠1与∠2互补,
(邻补角定义)
(同角的补角相等)
1
2
2
3
1
3
1、有公共顶点
分类
∠1和∠2、∠2和∠3、∠3和∠4、∠4和∠1
∠1和∠3、
∠2和∠4、
1、有公共顶点
位置关系
邻补角
对顶角
邻补角互补
2、有一条公共边
3、另一边互为反向延长线
2、没有公共边
两直线相交
3、两边互为反向延长线
名称
大小关系
对顶角相等
B
A
C
D
O
1
2
3
4
1
3
1
2
1、若∠1与∠2是对顶角,∠1=160,则∠2=______0;
若 ∠3与∠4是邻补角,则∠3+∠4 =______0
180
180
2、若∠1与∠2为对顶角,∠1与∠3互补,则 ∠2+∠3= 0
16
跟踪练习:
3.如图,点A,O,B在同一直线上,已知∠BOC=50°,
则∠AOC= °.
130
4.如图,直线AB和CD相交于点O,OE平分∠DOB,
∠AOC=40°,则∠DOE= .
20°
5.如图,已知直线AB,CD相交于点O,且∠EOD=∠DOB,
OF平分∠AOE,若∠AOC=28°,则∠EOF= .
62°
例1:如图,直线a、b相交。
(1) ∠ 1=400, 求∠2,∠3,∠4的度数。
(2) ∠1:∠2=2:7 ,求各角的度数。
∠2=180°-∠1
=180°- 40°
解:(1)由邻补角的定义,可得
=140°
由对顶角相等,可得
∠3=∠1=40°
∠4=∠2=140°
例题分析
2、如图,已知直线AB,CD相交于点O,OA平分∠EOC,∠EOC=700,求∠BOD,∠BOC的度数。
解:因为OA平分∠EOC,∠EOC= 700
所以∠AOC=350
由对顶角相等,得
由邻补角定义,得
∠BOC= 180°-∠AOC
= 180°- 35°
= 145°
∠BOD=∠AOC=350
1、如图1,三条直线AB、CD、
EF两两相交,在这个图形中,有
对顶角_____对,邻补角____ 对.
6
12
∠AOD
∠BOD
∠AOD
∠COE
∠3、
2、如图2,直线AB、CD
相交于O,OE是射线。则
∠3的对顶角是_____________,
∠1的对顶角是_____________,
∠1的邻补角是_____________,
∠2的邻补角是_____________。
课堂练习:
图1
图2
4、已知两条直线相交成的四个角,其中一个角是900,其余各角是_____ 。
900
850
5、如图4,三条直线a,b,c相交于点O,∠1=400,∠2=550,则∠3=_____.
3、如图3,∠2与∠3为邻补角,∠1=∠2,则∠1与∠3的关系为 。
互补
图3
图4
6.下列命题中,正确的是( )
A.有公共顶点,且方向相反的两个角是对顶角
B.有公共点,且又相等的角是对顶角
C.两条直线相交所成的角是对顶角
D.角的两边互为反向延长线的两个角是对顶角
D
7.下列图形中,∠1与∠2是对顶角的是( C )
1.如图是一个对顶角量角器,
你能说明它度量角度的原理吗?
拓展练习
拓展练习
2.找出图中∠AOE的对顶角及邻补角,
若没有请画出.
角的名称
邻补角
对顶角
位置关系
2、有一条公共边
3、另一边互为反向延长线4 .两条直线相交形成的角
1、有公共顶点
1、有公共顶点
2、没有公共边
3、两边互为反向延长线4. 两条直线相交而成;
性质
邻补角互补
对顶角相等
相同点
①都是两条直线相交而成的角; ②都有一个公共顶点;③都是成对出现的
不同点
1. 对 顶角没有公共边而邻补角有一条公共边;
2.两条直线相交时,一个角的对顶角只有一个,而一个角的邻补角有两个.
对顶角有两对,
邻补角有四对
知识回顾:
课堂小结
(1)对顶角与邻补角的概念
(2)能从图中辨认对顶角与邻补角.
(3)知道“对顶角相等”.
(4)了解“对顶角相等”的说理过程.
思考题:
两条直线相交于一点,有几对对顶角?
三条直线相交于一点,有几对对顶角?
四条直线相交于一点,有几对对顶角?
n 条直线相交于一点,有几对对顶角?
