2021-2022学年山东省烟台市龙口市九年级(上)期中数学试卷(五四学制)(Word版含解析)
文档属性
| 名称 | 2021-2022学年山东省烟台市龙口市九年级(上)期中数学试卷(五四学制)(Word版含解析) |  | |
| 格式 | doc | ||
| 文件大小 | 974.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(五四学制) | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-12-27 16:15:35 | ||
图片预览



文档简介
2021-2022学年山东省烟台市龙口市九年级第一学期期中数学试卷(五四学制)
一、选择题(每小题有且只有一个正确答案,请把正确答案的字母代号涂在答题纸上)
1.下列函数中自变量的取值范围是x>2的是( )
A.y=x﹣2 B.y= C.y= D.y=
2.若反比例函数y=(k≠0)的图象经过点P(2,5),则下列各点在这个函数图象上的是( )
A.(﹣5,﹣2) B.(5,﹣2) C.(2,﹣5) D.(﹣2,5)
3.如图,在△ABC中,∠A=90°,AC=6,AB=8,则sinC的值为( )
A. B. C. D.
4.已知抛物线y=﹣(x﹣1)2+2,则下列是该抛物线对称轴的是( )
A.直线x=﹣1 B.直线x=1 C.直线x=﹣2 D.直线x=2
5.已知反比例函数y=,下列结论中不正确的是( )
A.图象经过点(﹣1,﹣1)
B.当x<0时,y随着x的增大而增大
C.当x>1时,0<y<1
D.图象在第一、三象限
6.在△ABC中,∠A,∠B都是锐角,且sinA=,cosB=,则此三角形是( )
A.锐角三角形 B.直角三角形
C.钝角三角形 D.形状不能确定
7.若二次函数y=m﹣x在其图象对称轴的右侧,y随x的增大而减小,则m的值是( )
A.m<0 B.m=±2 C.m=2 D.m=﹣2
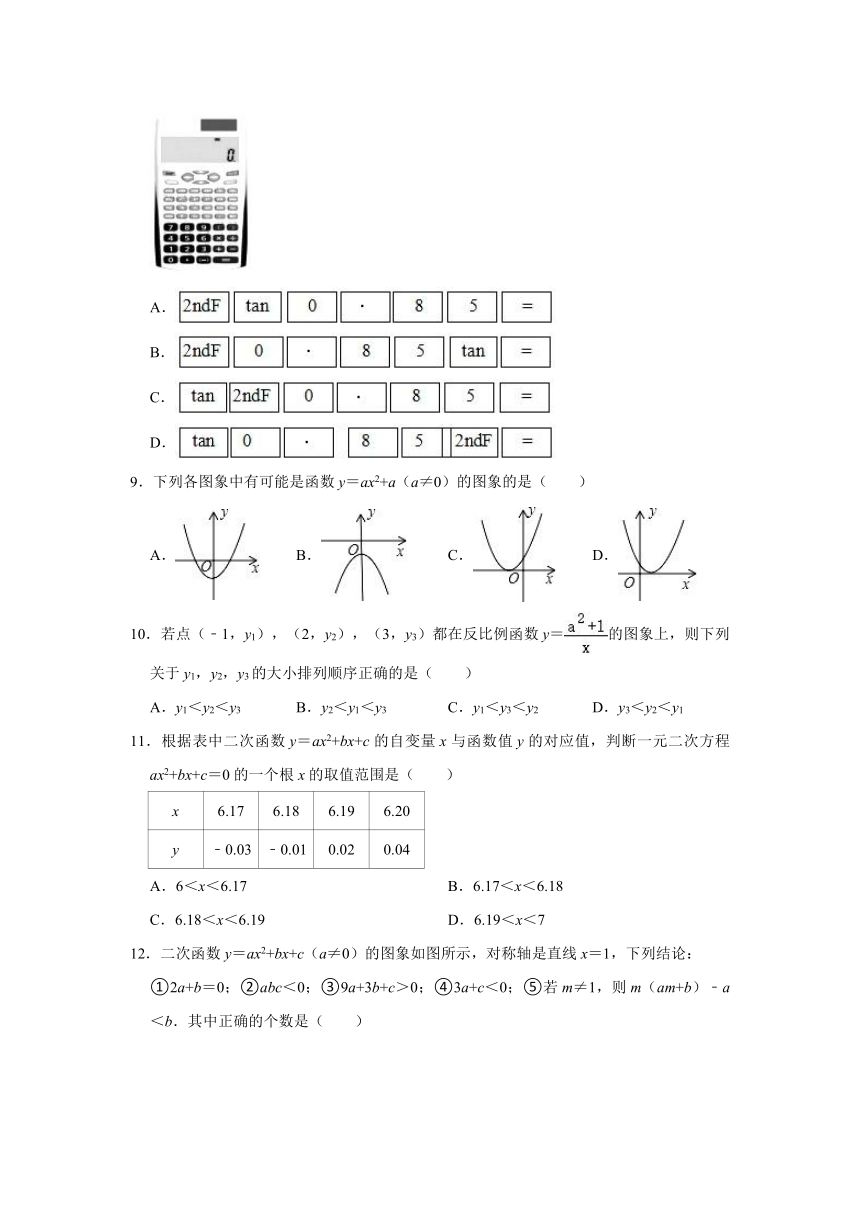
8.已知tanA=0.85,用计算器求∠A的大小,下列按键顺序正确的是( )
A.
B.
C.
D.
9.下列各图象中有可能是函数y=ax2+a(a≠0)的图象的是( )
A. B. C. D.
10.若点(﹣1,y1),(2,y2),(3,y3)都在反比例函数y=的图象上,则下列关于y1,y2,y3的大小排列顺序正确的是( )
A.y1<y2<y3 B.y2<y1<y3 C.y1<y3<y2 D.y3<y2<y1
11.根据表中二次函数y=ax2+bx+c的自变量x与函数值y的对应值,判断一元二次方程ax2+bx+c=0的一个根x的取值范围是( )
x 6.17 6.18 6.19 6.20
y ﹣0.03 ﹣0.01 0.02 0.04
A.6<x<6.17 B.6.17<x<6.18
C.6.18<x<6.19 D.6.19<x<7
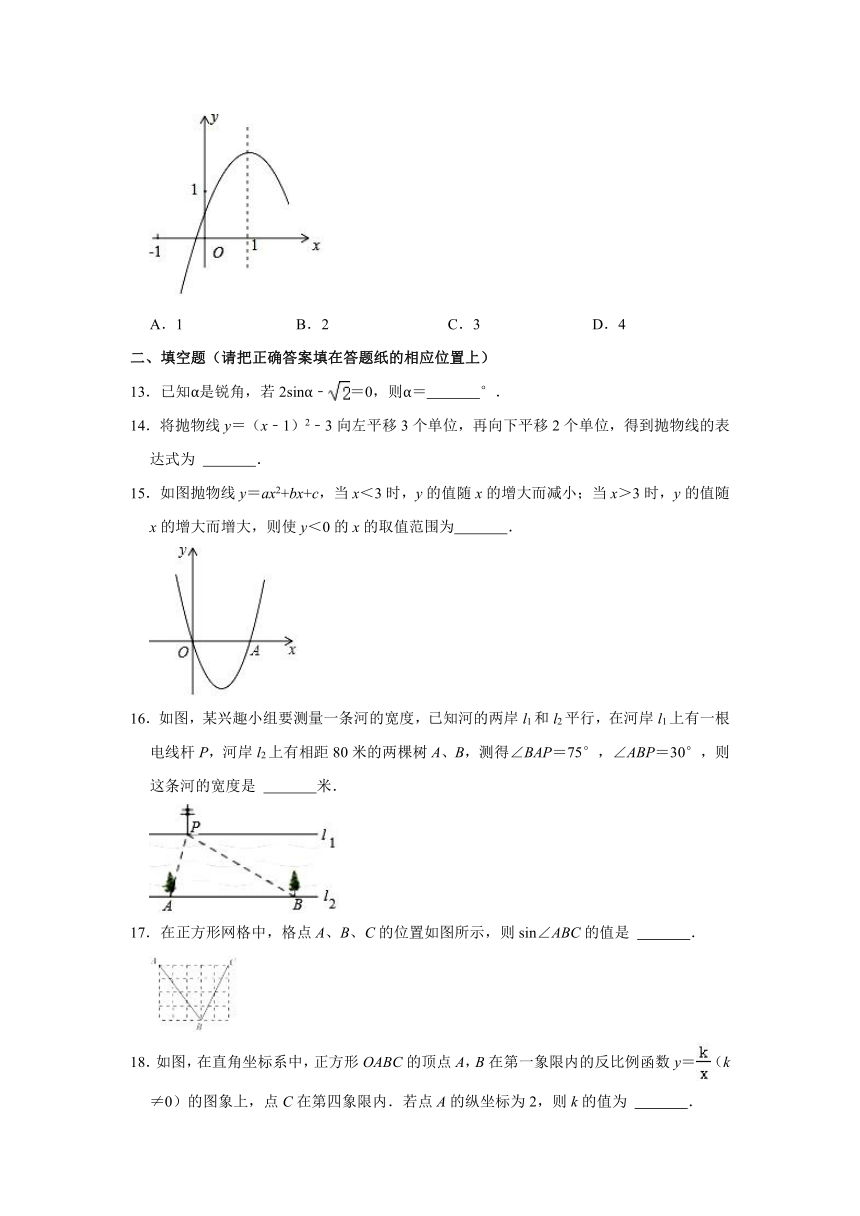
12.二次函数y=ax2+bx+c(a≠0)的图象如图所示,对称轴是直线x=1,下列结论:
①2a+b=0;②abc<0;③9a+3b+c>0;④3a+c<0;⑤若m≠1,则m(am+b)﹣a<b.其中正确的个数是( )
A.1 B.2 C.3 D.4
二、填空题(请把正确答案填在答题纸的相应位置上)
13.已知α是锐角,若2sinα﹣=0,则α= °.
14.将抛物线y=(x﹣1)2﹣3向左平移3个单位,再向下平移2个单位,得到抛物线的表达式为 .
15.如图抛物线y=ax2+bx+c,当x<3时,y的值随x的增大而减小;当x>3时,y的值随x的增大而增大,则使y<0的x的取值范围为 .
16.如图,某兴趣小组要测量一条河的宽度,已知河的两岸l1和l2平行,在河岸l1上有一根电线杆P,河岸l2上有相距80米的两棵树A、B,测得∠BAP=75°,∠ABP=30°,则这条河的宽度是 米.
17.在正方形网格中,格点A、B、C的位置如图所示,则sin∠ABC的值是 .
18.如图,在直角坐标系中,正方形OABC的顶点A,B在第一象限内的反比例函数y=(k≠0)的图象上,点C在第四象限内.若点A的纵坐标为2,则k的值为 .
三、解答题(请把解答过程写在答题纸的相应位置上)
19.计算:sin60° cos230°﹣.
20.已知在△ABC中,∠C=90°,,,解这个直角三角形.
21.某气球内充满了一定质量的气体,当温度不变时,气球内气体的气压P(千帕)是气体V(立方米)的反比例函数,其图象如图所示.
(1)求该反比例函数的关系式;
(2)当气球的体积是0.8立方米时,气球内的气压是多少千帕?
22.已知二次函数y=﹣2x2+4x.
(1)用配方法求这个二次函数图象的顶点坐标和对称轴;
(2)画出这个函数的大致图象(草图),指出函数值不小于0时,x的取值范围.
23.某客轮在C点失事后,海上搜救中心立即通知位于A,B两处的专业救助轮前往出事地点协助搜救,B在A的正东方向,且相距100海里.接到通知后,测得出事地点C在A的南偏东60°,C在B的南偏东30°,如果A,B两处救助轮航行速度都是25海里/时,试问A处救助轮赶到出事地点C需要多长时间?(结果保留根号)
24.如图,在平面直角坐标系中,一次函数y=2x+4的图象与x轴交于点A,与y轴交于点B,与反比例函数y=(k≠0)的图象交于C,D两点,点C的坐标为(n,6).
(1)求该反比例函数的表达式;
(2)求点D的坐标;
(3)连接OC,OD,求△COD的面积.
25.某商场要经营一种新上市的文具,进价为20元/件.试营销阶段发现:当销售单价是25元时,每天的销售量为250件;销售单价每上涨1元,每天的销售量就减少10件.
(1)写出商场销售这种文具,每天所得的销售利润w(元)与销售单价x(元)之间的函数关系式;
(2)求销售单价为多少元时,该文具每天的销售利润最大;
(3)商场的营销部结合上述情况,提出了A、B两种营销方案:
方案A:该文具的销售单价高于进价且不超过30元;
方案B:每天销售量不少于10件,且每件文具的利润至少为25元
请比较哪种方案的最大利润更高,并说明理由.
26.如图,抛物线y=ax2+bx+c与x轴交于A,B两点,与y轴交于C点,OA=1,OB=OC=3.
(1)求抛物线的表达式;
(2)如图1,点D为第一象限抛物线上一动点,连接DC,DB,BC,设点D的横坐标为m,△BCD的面积为S,求S的最大值;
(3)如图2,点P(0,n)是线段OC上一点(不与点O、C重合),连接PB,将线段PB以点P为中心,旋转90°得到线段PQ,是否存在n的值,使点Q落在抛物线上?若存在,请求出满足条件的n的值,若不存在,请说明理由.
参考答案
一、选择题(每小题有且只有一个正确答案,请把正确答案的字母代号涂在答题纸上)
1.下列函数中自变量的取值范围是x>2的是( )
A.y=x﹣2 B.y= C.y= D.y=
【分析】当函数表达式是整式时,自变量可取全体实数;当函数表达式是分式时,考虑分式的分母不能为0;当函数表达式是二次根式时,被开方数为非负数.
解:A、项中x的取值范围是全体实数;
B、项中x的取值范围是x≠2;
C、项中x的取值范围是x≥2;
D、项根据二次根式和分式的意义得x﹣2>0,解得:x>2.
故选:D.
2.若反比例函数y=(k≠0)的图象经过点P(2,5),则下列各点在这个函数图象上的是( )
A.(﹣5,﹣2) B.(5,﹣2) C.(2,﹣5) D.(﹣2,5)
【分析】由点P在反比例函数图象上可求出k的值,再求出四个选项中点的横纵坐标之积,比照后即可得出结论.
解:∵反比例函数y=(k≠0)的图象经过点P(2,5),
∴k=2×5=10.
A、﹣5×(﹣2)=10;
B、5×(﹣2)=﹣10;
C、2×(﹣5)=﹣10;
D、﹣2×5=﹣10.
故选:A.
3.如图,在△ABC中,∠A=90°,AC=6,AB=8,则sinC的值为( )
A. B. C. D.
【分析】先利用勾股定理计算出BC,然后根据正弦的定义求解.
解:∵∠A=90°,AC=6,AB=8,
∴BC==10,
∴sinC===.
故选:D.
4.已知抛物线y=﹣(x﹣1)2+2,则下列是该抛物线对称轴的是( )
A.直线x=﹣1 B.直线x=1 C.直线x=﹣2 D.直线x=2
【分析】根据题目中的抛物线,可以直接写出该抛物线的对称轴,本题得以解决.
解:∵抛物线y=﹣(x﹣1)2+2,
∴该抛物线的对称轴是直线x=1,
故选:B.
5.已知反比例函数y=,下列结论中不正确的是( )
A.图象经过点(﹣1,﹣1)
B.当x<0时,y随着x的增大而增大
C.当x>1时,0<y<1
D.图象在第一、三象限
【分析】根据反比例函数的性质对各选项进行逐一分析即可.
解:A、当x=﹣1时,y=﹣1,即图象经过点(﹣1,﹣1),不符合题意.
B、反比例函数y=中的k=1>0,则当x<0时,y随着x的增大而减小,符合题意.
C、当x>1时,0<y<1,不符合题意.
D、反比例函数y=中的k=1>0,则图象在第一、三象限,不符合题意.
故选:B.
6.在△ABC中,∠A,∠B都是锐角,且sinA=,cosB=,则此三角形是( )
A.锐角三角形 B.直角三角形
C.钝角三角形 D.形状不能确定
【分析】根据特殊角的三角函数值即可求得∠A和∠B的度数,然后求得∠C的度数,据此即可判断.
解:∵sinA=,cosB=,
∴∠A=30°,∠B=45°,
∴∠C=180°﹣30°﹣45°=105°.
故选:C.
7.若二次函数y=m﹣x在其图象对称轴的右侧,y随x的增大而减小,则m的值是( )
A.m<0 B.m=±2 C.m=2 D.m=﹣2
【分析】根据二次函数的定义条件列出方程求解则可.其图象对称轴的右侧,y随x的增大而减小,就说明图象开口向下,m<0.
解:∵二次函数y=m﹣x在其图象对称轴的右侧,y随x的增大而减小,
∴,
解得,m=﹣2,
故选:D.
8.已知tanA=0.85,用计算器求∠A的大小,下列按键顺序正确的是( )
A.
B.
C.
D.
【分析】直接根据计算器功能键判断.
解:根据计算器功能键,先按反三角2ndF,再按正切值.
故选:A.
9.下列各图象中有可能是函数y=ax2+a(a≠0)的图象的是( )
A. B. C. D.
【分析】从a>0和a<0两种情况进行分析图象的开口方向和顶点坐标,选出正确的答案.
解:当a>0时,开口向上,顶点在y轴的正半轴;
当a<0时,开口向下,顶点在y轴的负半轴,
故选:B.
10.若点(﹣1,y1),(2,y2),(3,y3)都在反比例函数y=的图象上,则下列关于y1,y2,y3的大小排列顺序正确的是( )
A.y1<y2<y3 B.y2<y1<y3 C.y1<y3<y2 D.y3<y2<y1
【分析】由k=a2+1>0,利用反比例函数的性质可得出y1<y3<y2,此题得解.
解:∵k=a2+1>0,
∴反比例函数的图象分别位于第一、三象限,且同一象限内y随x的增大而减小,
∵﹣1<0<2<3,
∴y1<y3<y2.
故选:C.
11.根据表中二次函数y=ax2+bx+c的自变量x与函数值y的对应值,判断一元二次方程ax2+bx+c=0的一个根x的取值范围是( )
x 6.17 6.18 6.19 6.20
y ﹣0.03 ﹣0.01 0.02 0.04
A.6<x<6.17 B.6.17<x<6.18
C.6.18<x<6.19 D.6.19<x<7
【分析】观察表格可知,y随x的值逐渐增大,ax2+bx+c的值在6.18~6.19之间由负到正,故可判断ax2+bx+c=0时,对应的x的值在6.18~6.19之间.
解:由表格中的数据看出﹣0.01和0.02更接近于0,故x应取对应的范围.
故选:C.
12.二次函数y=ax2+bx+c(a≠0)的图象如图所示,对称轴是直线x=1,下列结论:
①2a+b=0;②abc<0;③9a+3b+c>0;④3a+c<0;⑤若m≠1,则m(am+b)﹣a<b.其中正确的个数是( )
A.1 B.2 C.3 D.4
【分析】根据抛物线对称轴为直线x=﹣=1,可判断①,由抛物线开口方向,b=﹣2a,抛物线与y轴交点位置可判断②,由图象可得x=﹣1,y<0,根据抛物线对称性可得x=3,y<0,进而判断③④,由x=1时y取最大值可判断⑤.
解:∵抛物线对称轴为直线x=﹣=1,
∴b=﹣2a,
∴2a+b=0,①正确,符合题意.
∵抛物线开口向下,
∴a<0,
∵b=﹣2a,
∴b>0,
∵抛物线与x轴交点在x轴上方,
∴c>0,
∴abc<0,②正确,符合题意.
由图象可得x=﹣1时,y<0,根据抛物线对称性可得x=3时,y<0,
∴9a+3b+c<0,③错误,不符合题意.
∵x=﹣1,y<0,
∴a﹣b+c<0,
∵b=﹣2a,
∴3a+c<0,④正确,符合题意.
∵x=1时,y取最大值,
∴am2+bm+c≤a+b+c,
∴m(am+b)﹣a<b(m≠1),⑤正确,符合题意.
故选:D.
二、填空题(请把正确答案填在答题纸的相应位置上)
13.已知α是锐角,若2sinα﹣=0,则α= 45 °.
【分析】求出sinα的值,根据特殊锐角的三角函数值得出答案.
解:∵2sinα﹣=0,即sinα=,
∴α=45°,
故答案为:45.
14.将抛物线y=(x﹣1)2﹣3向左平移3个单位,再向下平移2个单位,得到抛物线的表达式为 y=(x+2)2﹣5 .
【分析】按照“左加右减,上加下减”的规律.
解:将抛物线y=(x﹣1)2﹣3向左平移3个单位,再向下平移2个单位,得y=(x﹣1+3)2﹣3﹣2;
故所得抛物线的解析式为y=(x+2)2﹣5.
故答案为:y=(x+2)2﹣5.
15.如图抛物线y=ax2+bx+c,当x<3时,y的值随x的增大而减小;当x>3时,y的值随x的增大而增大,则使y<0的x的取值范围为 0<x<6 .
【分析】求出抛物线与x轴的交点坐标即可解决问题.
解:由题意对称轴x=3,抛物线经过(0,0)和(6,0),
观察图象可知:使y<0的x的取值范围为0<x<6.
故答案为0<x<6.
16.如图,某兴趣小组要测量一条河的宽度,已知河的两岸l1和l2平行,在河岸l1上有一根电线杆P,河岸l2上有相距80米的两棵树A、B,测得∠BAP=75°,∠ABP=30°,则这条河的宽度是 40 米.
【分析】过点P作PC⊥AB,垂足为C.先判定△PAB是等腰三角形,再利用含30°角的直角三角形的性质求出河宽.
解:过点P作PC⊥AB,垂足为C.
∵∠BAP+∠ABP+∠APB=180°,
∴∠APB=180°﹣75°﹣30°=75°.
∴∠APB=∠PAB.
∴PB=BA=80(米).
在Rt△PBC中,
∵∠ABP=30°,
∴PC=PB=40(米).
故答案为:40.
17.在正方形网格中,格点A、B、C的位置如图所示,则sin∠ABC的值是 .
【分析】取格点D,连接CD,根据利用勾股定理可以求出BD、AD、AB的长度,再根据正弦函数的定义即可求出sin∠ABC的值.
解:如图,取格点D,连接CD.
由勾股定理得:
BD==,AD==2,AB==5,
∵()2+(2)2=52,
∴∠ADB=90°,
∴sin∠ABC==.
故答案为:.
18.如图,在直角坐标系中,正方形OABC的顶点A,B在第一象限内的反比例函数y=(k≠0)的图象上,点C在第四象限内.若点A的纵坐标为2,则k的值为 2﹣2 .
【分析】作AE⊥x轴于E,BF∥x轴,交AE于F,根据图象上点的坐标特征得出A(,2),证得△AOE≌△BAF(AAS),得出OE=AF,AE=BF,即可得到B(+2,2﹣),根据系数k的几何意义得到k=(+2)(2﹣),解得即可
解:作AE⊥x轴于E,BF∥x轴,交AE于F,
∵∠OAE+∠BAF=90°=∠OAE+∠AOE,
∴∠BAF=∠AOE,
在△AOE和△BAF中,
,
∴△AOE≌△BAF(AAS),
∴OE=AF,AE=BF,
∵点A,B在反比例函数y=(k≠0)的图象上,点A的纵坐标为2,
∴A(,2),
∴B(+2,2﹣),
∴k=(+2)(2﹣),
解得k=﹣2±2(负数舍去),
∴k=2﹣2,
故答案为:2﹣2.
三、解答题(请把解答过程写在答题纸的相应位置上)
19.计算:sin60° cos230°﹣.
【分析】直接利用特殊角的三角函数值分别代入,再利用二次根式混合运算法则计算得出答案.
解:原式=×()2﹣
=×﹣
=﹣
=﹣.
20.已知在△ABC中,∠C=90°,,,解这个直角三角形.
【分析】已知两边一角,我们可以利用三角函数求得一角,那么另一角自然求得,再利用勾股定理求得第三边.
解:∵,
∴∠A=60°,
∴∠B=90°﹣∠A=90°﹣60°=30°.
.
21.某气球内充满了一定质量的气体,当温度不变时,气球内气体的气压P(千帕)是气体V(立方米)的反比例函数,其图象如图所示.
(1)求该反比例函数的关系式;
(2)当气球的体积是0.8立方米时,气球内的气压是多少千帕?
【分析】(1)将已知点的坐标代入到反比例函数的一般形式中即可求得其解析式;
(2)代入V=0.8求得压强即可.
解:(1)设表达式为P=,
∵图象经过点(2.5,64),
∴k=2.5×64=160,
所以表达式为P=;
(2)当V=0.8时,P==200(千帕).
22.已知二次函数y=﹣2x2+4x.
(1)用配方法求这个二次函数图象的顶点坐标和对称轴;
(2)画出这个函数的大致图象(草图),指出函数值不小于0时,x的取值范围.
【分析】(1)通过配方法把函数解析式转化为顶点式,可直接得出函数的顶点坐标及对称轴.
(2)根据顶点及对称轴的位置可画出草图;结合函数图象,可得出结论.
解:(1)y=﹣2x2+4x=﹣2(x2﹣2x+1)+2=﹣2(x﹣1)2+2,
这个二次函数图象的顶点坐标为(1,2),
对称轴为直线x=1.
(2)图象如下图所示,
由图象可知,函数值不小于0时,0≤x≤2.
23.某客轮在C点失事后,海上搜救中心立即通知位于A,B两处的专业救助轮前往出事地点协助搜救,B在A的正东方向,且相距100海里.接到通知后,测得出事地点C在A的南偏东60°,C在B的南偏东30°,如果A,B两处救助轮航行速度都是25海里/时,试问A处救助轮赶到出事地点C需要多长时间?(结果保留根号)
【分析】先根据等腰三角形的性质求出BC的长,过点C作AB的延长线的垂线,垂足为D,由直角三角形的性质求出BD的长,进而可得出AD的长,由锐角三角函数的定义得出AC的长,由此可得出结论.
解:根据题意可知,∠BAC=30°,∠ABC=120°,AB=100,
∴∠ACB=180°﹣30°﹣120°=30°,
∵A,B两处救助轮航行速度都是25海里/时,
∴BC=AB=100,
过点C作CD⊥AB交AB的延长线于点D,
∵∠CBD=60°,BC=100,
∴BD=BCcos60°=100×=50,
∴AD=AB+BD=150,
∵∠BAC=90°﹣60°=30°,
∴=cos30°,
∴AC==100,
∵A,B处救助轮的行使速度为25海里/时,
∴A处救助轮到达C点的时间是=4(小时).
24.如图,在平面直角坐标系中,一次函数y=2x+4的图象与x轴交于点A,与y轴交于点B,与反比例函数y=(k≠0)的图象交于C,D两点,点C的坐标为(n,6).
(1)求该反比例函数的表达式;
(2)求点D的坐标;
(3)连接OC,OD,求△COD的面积.
【分析】(1)将C(n,6)代入一次函数解析式中,再将所求坐标代入反比例函数解析式求解.
(2)联立一次函数与反比例函数方程求解.
(3)根据S△COD=S△CAO+S△DAO求解.
解:(1)∵点C(n,6)在一次函数y=2x+4的图象上,
∴6=2n+4,
∴n=1,
∴点C坐标为(1,6).
把点C坐标(1,6)代入y=,得k=6,
∴反比例函数的表达式为y=.
(2)令2x+4=,
解得x1=﹣3,x2=1,
当x=﹣3时,y=2×(﹣3)+4=﹣2,
∴点D的坐标是(﹣3,﹣2).
(3)S△COD=S△CAO+S△DAO=OA yC+OA (﹣yD)=+=8.
25.某商场要经营一种新上市的文具,进价为20元/件.试营销阶段发现:当销售单价是25元时,每天的销售量为250件;销售单价每上涨1元,每天的销售量就减少10件.
(1)写出商场销售这种文具,每天所得的销售利润w(元)与销售单价x(元)之间的函数关系式;
(2)求销售单价为多少元时,该文具每天的销售利润最大;
(3)商场的营销部结合上述情况,提出了A、B两种营销方案:
方案A:该文具的销售单价高于进价且不超过30元;
方案B:每天销售量不少于10件,且每件文具的利润至少为25元
请比较哪种方案的最大利润更高,并说明理由.
【分析】(1)根据利润=(销售单价﹣进价)×销售量,列出函数关系式即可;
(2)根据(1)式列出的函数关系式,运用配方法求最大值;
(3)分别求出方案A、B中x的取值范围,然后分别求出A、B方案的最大利润,然后进行比较.
解:(1)由题意得,销售量=250﹣10(x﹣25)=﹣10x+500,
则w=(x﹣20)(﹣10x+500)
=﹣10x2+700x﹣10000;
(2)w=﹣10x2+700x﹣10000=﹣10(x﹣35)2+2250.
∵﹣10<0,
∴函数图象开口向下,w有最大值,
当x=35时,w最大=2250,
故当单价为35元时,该文具每天的利润最大;
(3)A方案利润高.理由如下:
A方案中:20<x≤30,
故当x=30时,w有最大值,
此时wA=2000;
B方案中:,
故x的取值范围为:45≤x≤49,
∵函数w=﹣10(x﹣35)2+2250,对称轴为直线x=35,
∴当x=45时,w有最大值,
此时wB=1250,
∵wA>wB,
∴A方案利润更高.
26.如图,抛物线y=ax2+bx+c与x轴交于A,B两点,与y轴交于C点,OA=1,OB=OC=3.
(1)求抛物线的表达式;
(2)如图1,点D为第一象限抛物线上一动点,连接DC,DB,BC,设点D的横坐标为m,△BCD的面积为S,求S的最大值;
(3)如图2,点P(0,n)是线段OC上一点(不与点O、C重合),连接PB,将线段PB以点P为中心,旋转90°得到线段PQ,是否存在n的值,使点Q落在抛物线上?若存在,请求出满足条件的n的值,若不存在,请说明理由.
【分析】(1)根据OA=1,OB=OC=3得A(﹣1,0),B(3,0),C(0,3),再由待定系数法即可求出解析式;
(2)作DF⊥x轴于点F,交BC于点E,根据S=S△ADE+S△BDE=DE OF+DE BF=DE OB,表示出DE,再配方即可求得S最大值;
(3)过点P作PB的垂线,交抛物线于点Q1和Q2,作Q1M⊥y轴于点M,Q2N⊥y轴于点N.先证明△Q1PM≌△PBO,△Q1PM≌△PBO,进而得MQ1=OP=n,MP=OB=3,表示出Q1、Q2的坐标,代入抛物线即可求得N.
解:(1)∵OA=1,OB=OC=3.
∴A(﹣1,0),B(3,0),C(0,3),
∴设y=a(x+1)(x﹣3),
把C(0,3)代入得0=a×1×(﹣3),
解得a=﹣1,
∴y=﹣x2+2x+3;
(2)如图,作DF⊥x轴于点F,交BC于点E,
设直线BC关系式为y=kx+3,
代入B(3,0),
得3k+3=0,
解得k=﹣1,
∴直线BC:y=﹣x+3.
∵点D的横坐标为m,则DF=﹣m2+2m+3,EF=﹣m+3,
∴DE=﹣m2+3m,
∴S=S△ADE+S△BDE=DE OF+DE BF,
=DE OB=(﹣m2+3m)
=﹣(m﹣)2+,
∵﹣<0,
∴S的最大值是;
(3)如图,过点P作PB的垂线,交抛物线于点Q1和Q2,作Q1M⊥y轴于点M,Q2N⊥y轴于点N.
∴∠Q1MP=∠Q2NP=∠BOP=90°,
∵∠Q1PM+∠PQ1M=90°,∠Q1PM+∠BPO=90°,
∴∠PQ1M=∠BPO,
又BP=PQ1,
∴△Q1PM≌△PBO(AAS),
∴MQ1=OP=n,MP=OB=3,
∴Q1(n,n+3),
代入抛物线,得n+3=﹣n2+2n+3,
解得n=1或n=0,
同理,△Q2PN≌△PBO(AAS),
∴Q2(﹣n,n﹣3),
代入抛物线,得n﹣3=﹣n2﹣2n+3,
解得n=或,
综上,存在n 且n=1或n=.
一、选择题(每小题有且只有一个正确答案,请把正确答案的字母代号涂在答题纸上)
1.下列函数中自变量的取值范围是x>2的是( )
A.y=x﹣2 B.y= C.y= D.y=
2.若反比例函数y=(k≠0)的图象经过点P(2,5),则下列各点在这个函数图象上的是( )
A.(﹣5,﹣2) B.(5,﹣2) C.(2,﹣5) D.(﹣2,5)
3.如图,在△ABC中,∠A=90°,AC=6,AB=8,则sinC的值为( )
A. B. C. D.
4.已知抛物线y=﹣(x﹣1)2+2,则下列是该抛物线对称轴的是( )
A.直线x=﹣1 B.直线x=1 C.直线x=﹣2 D.直线x=2
5.已知反比例函数y=,下列结论中不正确的是( )
A.图象经过点(﹣1,﹣1)
B.当x<0时,y随着x的增大而增大
C.当x>1时,0<y<1
D.图象在第一、三象限
6.在△ABC中,∠A,∠B都是锐角,且sinA=,cosB=,则此三角形是( )
A.锐角三角形 B.直角三角形
C.钝角三角形 D.形状不能确定
7.若二次函数y=m﹣x在其图象对称轴的右侧,y随x的增大而减小,则m的值是( )
A.m<0 B.m=±2 C.m=2 D.m=﹣2
8.已知tanA=0.85,用计算器求∠A的大小,下列按键顺序正确的是( )
A.
B.
C.
D.
9.下列各图象中有可能是函数y=ax2+a(a≠0)的图象的是( )
A. B. C. D.
10.若点(﹣1,y1),(2,y2),(3,y3)都在反比例函数y=的图象上,则下列关于y1,y2,y3的大小排列顺序正确的是( )
A.y1<y2<y3 B.y2<y1<y3 C.y1<y3<y2 D.y3<y2<y1
11.根据表中二次函数y=ax2+bx+c的自变量x与函数值y的对应值,判断一元二次方程ax2+bx+c=0的一个根x的取值范围是( )
x 6.17 6.18 6.19 6.20
y ﹣0.03 ﹣0.01 0.02 0.04
A.6<x<6.17 B.6.17<x<6.18
C.6.18<x<6.19 D.6.19<x<7
12.二次函数y=ax2+bx+c(a≠0)的图象如图所示,对称轴是直线x=1,下列结论:
①2a+b=0;②abc<0;③9a+3b+c>0;④3a+c<0;⑤若m≠1,则m(am+b)﹣a<b.其中正确的个数是( )
A.1 B.2 C.3 D.4
二、填空题(请把正确答案填在答题纸的相应位置上)
13.已知α是锐角,若2sinα﹣=0,则α= °.
14.将抛物线y=(x﹣1)2﹣3向左平移3个单位,再向下平移2个单位,得到抛物线的表达式为 .
15.如图抛物线y=ax2+bx+c,当x<3时,y的值随x的增大而减小;当x>3时,y的值随x的增大而增大,则使y<0的x的取值范围为 .
16.如图,某兴趣小组要测量一条河的宽度,已知河的两岸l1和l2平行,在河岸l1上有一根电线杆P,河岸l2上有相距80米的两棵树A、B,测得∠BAP=75°,∠ABP=30°,则这条河的宽度是 米.
17.在正方形网格中,格点A、B、C的位置如图所示,则sin∠ABC的值是 .
18.如图,在直角坐标系中,正方形OABC的顶点A,B在第一象限内的反比例函数y=(k≠0)的图象上,点C在第四象限内.若点A的纵坐标为2,则k的值为 .
三、解答题(请把解答过程写在答题纸的相应位置上)
19.计算:sin60° cos230°﹣.
20.已知在△ABC中,∠C=90°,,,解这个直角三角形.
21.某气球内充满了一定质量的气体,当温度不变时,气球内气体的气压P(千帕)是气体V(立方米)的反比例函数,其图象如图所示.
(1)求该反比例函数的关系式;
(2)当气球的体积是0.8立方米时,气球内的气压是多少千帕?
22.已知二次函数y=﹣2x2+4x.
(1)用配方法求这个二次函数图象的顶点坐标和对称轴;
(2)画出这个函数的大致图象(草图),指出函数值不小于0时,x的取值范围.
23.某客轮在C点失事后,海上搜救中心立即通知位于A,B两处的专业救助轮前往出事地点协助搜救,B在A的正东方向,且相距100海里.接到通知后,测得出事地点C在A的南偏东60°,C在B的南偏东30°,如果A,B两处救助轮航行速度都是25海里/时,试问A处救助轮赶到出事地点C需要多长时间?(结果保留根号)
24.如图,在平面直角坐标系中,一次函数y=2x+4的图象与x轴交于点A,与y轴交于点B,与反比例函数y=(k≠0)的图象交于C,D两点,点C的坐标为(n,6).
(1)求该反比例函数的表达式;
(2)求点D的坐标;
(3)连接OC,OD,求△COD的面积.
25.某商场要经营一种新上市的文具,进价为20元/件.试营销阶段发现:当销售单价是25元时,每天的销售量为250件;销售单价每上涨1元,每天的销售量就减少10件.
(1)写出商场销售这种文具,每天所得的销售利润w(元)与销售单价x(元)之间的函数关系式;
(2)求销售单价为多少元时,该文具每天的销售利润最大;
(3)商场的营销部结合上述情况,提出了A、B两种营销方案:
方案A:该文具的销售单价高于进价且不超过30元;
方案B:每天销售量不少于10件,且每件文具的利润至少为25元
请比较哪种方案的最大利润更高,并说明理由.
26.如图,抛物线y=ax2+bx+c与x轴交于A,B两点,与y轴交于C点,OA=1,OB=OC=3.
(1)求抛物线的表达式;
(2)如图1,点D为第一象限抛物线上一动点,连接DC,DB,BC,设点D的横坐标为m,△BCD的面积为S,求S的最大值;
(3)如图2,点P(0,n)是线段OC上一点(不与点O、C重合),连接PB,将线段PB以点P为中心,旋转90°得到线段PQ,是否存在n的值,使点Q落在抛物线上?若存在,请求出满足条件的n的值,若不存在,请说明理由.
参考答案
一、选择题(每小题有且只有一个正确答案,请把正确答案的字母代号涂在答题纸上)
1.下列函数中自变量的取值范围是x>2的是( )
A.y=x﹣2 B.y= C.y= D.y=
【分析】当函数表达式是整式时,自变量可取全体实数;当函数表达式是分式时,考虑分式的分母不能为0;当函数表达式是二次根式时,被开方数为非负数.
解:A、项中x的取值范围是全体实数;
B、项中x的取值范围是x≠2;
C、项中x的取值范围是x≥2;
D、项根据二次根式和分式的意义得x﹣2>0,解得:x>2.
故选:D.
2.若反比例函数y=(k≠0)的图象经过点P(2,5),则下列各点在这个函数图象上的是( )
A.(﹣5,﹣2) B.(5,﹣2) C.(2,﹣5) D.(﹣2,5)
【分析】由点P在反比例函数图象上可求出k的值,再求出四个选项中点的横纵坐标之积,比照后即可得出结论.
解:∵反比例函数y=(k≠0)的图象经过点P(2,5),
∴k=2×5=10.
A、﹣5×(﹣2)=10;
B、5×(﹣2)=﹣10;
C、2×(﹣5)=﹣10;
D、﹣2×5=﹣10.
故选:A.
3.如图,在△ABC中,∠A=90°,AC=6,AB=8,则sinC的值为( )
A. B. C. D.
【分析】先利用勾股定理计算出BC,然后根据正弦的定义求解.
解:∵∠A=90°,AC=6,AB=8,
∴BC==10,
∴sinC===.
故选:D.
4.已知抛物线y=﹣(x﹣1)2+2,则下列是该抛物线对称轴的是( )
A.直线x=﹣1 B.直线x=1 C.直线x=﹣2 D.直线x=2
【分析】根据题目中的抛物线,可以直接写出该抛物线的对称轴,本题得以解决.
解:∵抛物线y=﹣(x﹣1)2+2,
∴该抛物线的对称轴是直线x=1,
故选:B.
5.已知反比例函数y=,下列结论中不正确的是( )
A.图象经过点(﹣1,﹣1)
B.当x<0时,y随着x的增大而增大
C.当x>1时,0<y<1
D.图象在第一、三象限
【分析】根据反比例函数的性质对各选项进行逐一分析即可.
解:A、当x=﹣1时,y=﹣1,即图象经过点(﹣1,﹣1),不符合题意.
B、反比例函数y=中的k=1>0,则当x<0时,y随着x的增大而减小,符合题意.
C、当x>1时,0<y<1,不符合题意.
D、反比例函数y=中的k=1>0,则图象在第一、三象限,不符合题意.
故选:B.
6.在△ABC中,∠A,∠B都是锐角,且sinA=,cosB=,则此三角形是( )
A.锐角三角形 B.直角三角形
C.钝角三角形 D.形状不能确定
【分析】根据特殊角的三角函数值即可求得∠A和∠B的度数,然后求得∠C的度数,据此即可判断.
解:∵sinA=,cosB=,
∴∠A=30°,∠B=45°,
∴∠C=180°﹣30°﹣45°=105°.
故选:C.
7.若二次函数y=m﹣x在其图象对称轴的右侧,y随x的增大而减小,则m的值是( )
A.m<0 B.m=±2 C.m=2 D.m=﹣2
【分析】根据二次函数的定义条件列出方程求解则可.其图象对称轴的右侧,y随x的增大而减小,就说明图象开口向下,m<0.
解:∵二次函数y=m﹣x在其图象对称轴的右侧,y随x的增大而减小,
∴,
解得,m=﹣2,
故选:D.
8.已知tanA=0.85,用计算器求∠A的大小,下列按键顺序正确的是( )
A.
B.
C.
D.
【分析】直接根据计算器功能键判断.
解:根据计算器功能键,先按反三角2ndF,再按正切值.
故选:A.
9.下列各图象中有可能是函数y=ax2+a(a≠0)的图象的是( )
A. B. C. D.
【分析】从a>0和a<0两种情况进行分析图象的开口方向和顶点坐标,选出正确的答案.
解:当a>0时,开口向上,顶点在y轴的正半轴;
当a<0时,开口向下,顶点在y轴的负半轴,
故选:B.
10.若点(﹣1,y1),(2,y2),(3,y3)都在反比例函数y=的图象上,则下列关于y1,y2,y3的大小排列顺序正确的是( )
A.y1<y2<y3 B.y2<y1<y3 C.y1<y3<y2 D.y3<y2<y1
【分析】由k=a2+1>0,利用反比例函数的性质可得出y1<y3<y2,此题得解.
解:∵k=a2+1>0,
∴反比例函数的图象分别位于第一、三象限,且同一象限内y随x的增大而减小,
∵﹣1<0<2<3,
∴y1<y3<y2.
故选:C.
11.根据表中二次函数y=ax2+bx+c的自变量x与函数值y的对应值,判断一元二次方程ax2+bx+c=0的一个根x的取值范围是( )
x 6.17 6.18 6.19 6.20
y ﹣0.03 ﹣0.01 0.02 0.04
A.6<x<6.17 B.6.17<x<6.18
C.6.18<x<6.19 D.6.19<x<7
【分析】观察表格可知,y随x的值逐渐增大,ax2+bx+c的值在6.18~6.19之间由负到正,故可判断ax2+bx+c=0时,对应的x的值在6.18~6.19之间.
解:由表格中的数据看出﹣0.01和0.02更接近于0,故x应取对应的范围.
故选:C.
12.二次函数y=ax2+bx+c(a≠0)的图象如图所示,对称轴是直线x=1,下列结论:
①2a+b=0;②abc<0;③9a+3b+c>0;④3a+c<0;⑤若m≠1,则m(am+b)﹣a<b.其中正确的个数是( )
A.1 B.2 C.3 D.4
【分析】根据抛物线对称轴为直线x=﹣=1,可判断①,由抛物线开口方向,b=﹣2a,抛物线与y轴交点位置可判断②,由图象可得x=﹣1,y<0,根据抛物线对称性可得x=3,y<0,进而判断③④,由x=1时y取最大值可判断⑤.
解:∵抛物线对称轴为直线x=﹣=1,
∴b=﹣2a,
∴2a+b=0,①正确,符合题意.
∵抛物线开口向下,
∴a<0,
∵b=﹣2a,
∴b>0,
∵抛物线与x轴交点在x轴上方,
∴c>0,
∴abc<0,②正确,符合题意.
由图象可得x=﹣1时,y<0,根据抛物线对称性可得x=3时,y<0,
∴9a+3b+c<0,③错误,不符合题意.
∵x=﹣1,y<0,
∴a﹣b+c<0,
∵b=﹣2a,
∴3a+c<0,④正确,符合题意.
∵x=1时,y取最大值,
∴am2+bm+c≤a+b+c,
∴m(am+b)﹣a<b(m≠1),⑤正确,符合题意.
故选:D.
二、填空题(请把正确答案填在答题纸的相应位置上)
13.已知α是锐角,若2sinα﹣=0,则α= 45 °.
【分析】求出sinα的值,根据特殊锐角的三角函数值得出答案.
解:∵2sinα﹣=0,即sinα=,
∴α=45°,
故答案为:45.
14.将抛物线y=(x﹣1)2﹣3向左平移3个单位,再向下平移2个单位,得到抛物线的表达式为 y=(x+2)2﹣5 .
【分析】按照“左加右减,上加下减”的规律.
解:将抛物线y=(x﹣1)2﹣3向左平移3个单位,再向下平移2个单位,得y=(x﹣1+3)2﹣3﹣2;
故所得抛物线的解析式为y=(x+2)2﹣5.
故答案为:y=(x+2)2﹣5.
15.如图抛物线y=ax2+bx+c,当x<3时,y的值随x的增大而减小;当x>3时,y的值随x的增大而增大,则使y<0的x的取值范围为 0<x<6 .
【分析】求出抛物线与x轴的交点坐标即可解决问题.
解:由题意对称轴x=3,抛物线经过(0,0)和(6,0),
观察图象可知:使y<0的x的取值范围为0<x<6.
故答案为0<x<6.
16.如图,某兴趣小组要测量一条河的宽度,已知河的两岸l1和l2平行,在河岸l1上有一根电线杆P,河岸l2上有相距80米的两棵树A、B,测得∠BAP=75°,∠ABP=30°,则这条河的宽度是 40 米.
【分析】过点P作PC⊥AB,垂足为C.先判定△PAB是等腰三角形,再利用含30°角的直角三角形的性质求出河宽.
解:过点P作PC⊥AB,垂足为C.
∵∠BAP+∠ABP+∠APB=180°,
∴∠APB=180°﹣75°﹣30°=75°.
∴∠APB=∠PAB.
∴PB=BA=80(米).
在Rt△PBC中,
∵∠ABP=30°,
∴PC=PB=40(米).
故答案为:40.
17.在正方形网格中,格点A、B、C的位置如图所示,则sin∠ABC的值是 .
【分析】取格点D,连接CD,根据利用勾股定理可以求出BD、AD、AB的长度,再根据正弦函数的定义即可求出sin∠ABC的值.
解:如图,取格点D,连接CD.
由勾股定理得:
BD==,AD==2,AB==5,
∵()2+(2)2=52,
∴∠ADB=90°,
∴sin∠ABC==.
故答案为:.
18.如图,在直角坐标系中,正方形OABC的顶点A,B在第一象限内的反比例函数y=(k≠0)的图象上,点C在第四象限内.若点A的纵坐标为2,则k的值为 2﹣2 .
【分析】作AE⊥x轴于E,BF∥x轴,交AE于F,根据图象上点的坐标特征得出A(,2),证得△AOE≌△BAF(AAS),得出OE=AF,AE=BF,即可得到B(+2,2﹣),根据系数k的几何意义得到k=(+2)(2﹣),解得即可
解:作AE⊥x轴于E,BF∥x轴,交AE于F,
∵∠OAE+∠BAF=90°=∠OAE+∠AOE,
∴∠BAF=∠AOE,
在△AOE和△BAF中,
,
∴△AOE≌△BAF(AAS),
∴OE=AF,AE=BF,
∵点A,B在反比例函数y=(k≠0)的图象上,点A的纵坐标为2,
∴A(,2),
∴B(+2,2﹣),
∴k=(+2)(2﹣),
解得k=﹣2±2(负数舍去),
∴k=2﹣2,
故答案为:2﹣2.
三、解答题(请把解答过程写在答题纸的相应位置上)
19.计算:sin60° cos230°﹣.
【分析】直接利用特殊角的三角函数值分别代入,再利用二次根式混合运算法则计算得出答案.
解:原式=×()2﹣
=×﹣
=﹣
=﹣.
20.已知在△ABC中,∠C=90°,,,解这个直角三角形.
【分析】已知两边一角,我们可以利用三角函数求得一角,那么另一角自然求得,再利用勾股定理求得第三边.
解:∵,
∴∠A=60°,
∴∠B=90°﹣∠A=90°﹣60°=30°.
.
21.某气球内充满了一定质量的气体,当温度不变时,气球内气体的气压P(千帕)是气体V(立方米)的反比例函数,其图象如图所示.
(1)求该反比例函数的关系式;
(2)当气球的体积是0.8立方米时,气球内的气压是多少千帕?
【分析】(1)将已知点的坐标代入到反比例函数的一般形式中即可求得其解析式;
(2)代入V=0.8求得压强即可.
解:(1)设表达式为P=,
∵图象经过点(2.5,64),
∴k=2.5×64=160,
所以表达式为P=;
(2)当V=0.8时,P==200(千帕).
22.已知二次函数y=﹣2x2+4x.
(1)用配方法求这个二次函数图象的顶点坐标和对称轴;
(2)画出这个函数的大致图象(草图),指出函数值不小于0时,x的取值范围.
【分析】(1)通过配方法把函数解析式转化为顶点式,可直接得出函数的顶点坐标及对称轴.
(2)根据顶点及对称轴的位置可画出草图;结合函数图象,可得出结论.
解:(1)y=﹣2x2+4x=﹣2(x2﹣2x+1)+2=﹣2(x﹣1)2+2,
这个二次函数图象的顶点坐标为(1,2),
对称轴为直线x=1.
(2)图象如下图所示,
由图象可知,函数值不小于0时,0≤x≤2.
23.某客轮在C点失事后,海上搜救中心立即通知位于A,B两处的专业救助轮前往出事地点协助搜救,B在A的正东方向,且相距100海里.接到通知后,测得出事地点C在A的南偏东60°,C在B的南偏东30°,如果A,B两处救助轮航行速度都是25海里/时,试问A处救助轮赶到出事地点C需要多长时间?(结果保留根号)
【分析】先根据等腰三角形的性质求出BC的长,过点C作AB的延长线的垂线,垂足为D,由直角三角形的性质求出BD的长,进而可得出AD的长,由锐角三角函数的定义得出AC的长,由此可得出结论.
解:根据题意可知,∠BAC=30°,∠ABC=120°,AB=100,
∴∠ACB=180°﹣30°﹣120°=30°,
∵A,B两处救助轮航行速度都是25海里/时,
∴BC=AB=100,
过点C作CD⊥AB交AB的延长线于点D,
∵∠CBD=60°,BC=100,
∴BD=BCcos60°=100×=50,
∴AD=AB+BD=150,
∵∠BAC=90°﹣60°=30°,
∴=cos30°,
∴AC==100,
∵A,B处救助轮的行使速度为25海里/时,
∴A处救助轮到达C点的时间是=4(小时).
24.如图,在平面直角坐标系中,一次函数y=2x+4的图象与x轴交于点A,与y轴交于点B,与反比例函数y=(k≠0)的图象交于C,D两点,点C的坐标为(n,6).
(1)求该反比例函数的表达式;
(2)求点D的坐标;
(3)连接OC,OD,求△COD的面积.
【分析】(1)将C(n,6)代入一次函数解析式中,再将所求坐标代入反比例函数解析式求解.
(2)联立一次函数与反比例函数方程求解.
(3)根据S△COD=S△CAO+S△DAO求解.
解:(1)∵点C(n,6)在一次函数y=2x+4的图象上,
∴6=2n+4,
∴n=1,
∴点C坐标为(1,6).
把点C坐标(1,6)代入y=,得k=6,
∴反比例函数的表达式为y=.
(2)令2x+4=,
解得x1=﹣3,x2=1,
当x=﹣3时,y=2×(﹣3)+4=﹣2,
∴点D的坐标是(﹣3,﹣2).
(3)S△COD=S△CAO+S△DAO=OA yC+OA (﹣yD)=+=8.
25.某商场要经营一种新上市的文具,进价为20元/件.试营销阶段发现:当销售单价是25元时,每天的销售量为250件;销售单价每上涨1元,每天的销售量就减少10件.
(1)写出商场销售这种文具,每天所得的销售利润w(元)与销售单价x(元)之间的函数关系式;
(2)求销售单价为多少元时,该文具每天的销售利润最大;
(3)商场的营销部结合上述情况,提出了A、B两种营销方案:
方案A:该文具的销售单价高于进价且不超过30元;
方案B:每天销售量不少于10件,且每件文具的利润至少为25元
请比较哪种方案的最大利润更高,并说明理由.
【分析】(1)根据利润=(销售单价﹣进价)×销售量,列出函数关系式即可;
(2)根据(1)式列出的函数关系式,运用配方法求最大值;
(3)分别求出方案A、B中x的取值范围,然后分别求出A、B方案的最大利润,然后进行比较.
解:(1)由题意得,销售量=250﹣10(x﹣25)=﹣10x+500,
则w=(x﹣20)(﹣10x+500)
=﹣10x2+700x﹣10000;
(2)w=﹣10x2+700x﹣10000=﹣10(x﹣35)2+2250.
∵﹣10<0,
∴函数图象开口向下,w有最大值,
当x=35时,w最大=2250,
故当单价为35元时,该文具每天的利润最大;
(3)A方案利润高.理由如下:
A方案中:20<x≤30,
故当x=30时,w有最大值,
此时wA=2000;
B方案中:,
故x的取值范围为:45≤x≤49,
∵函数w=﹣10(x﹣35)2+2250,对称轴为直线x=35,
∴当x=45时,w有最大值,
此时wB=1250,
∵wA>wB,
∴A方案利润更高.
26.如图,抛物线y=ax2+bx+c与x轴交于A,B两点,与y轴交于C点,OA=1,OB=OC=3.
(1)求抛物线的表达式;
(2)如图1,点D为第一象限抛物线上一动点,连接DC,DB,BC,设点D的横坐标为m,△BCD的面积为S,求S的最大值;
(3)如图2,点P(0,n)是线段OC上一点(不与点O、C重合),连接PB,将线段PB以点P为中心,旋转90°得到线段PQ,是否存在n的值,使点Q落在抛物线上?若存在,请求出满足条件的n的值,若不存在,请说明理由.
【分析】(1)根据OA=1,OB=OC=3得A(﹣1,0),B(3,0),C(0,3),再由待定系数法即可求出解析式;
(2)作DF⊥x轴于点F,交BC于点E,根据S=S△ADE+S△BDE=DE OF+DE BF=DE OB,表示出DE,再配方即可求得S最大值;
(3)过点P作PB的垂线,交抛物线于点Q1和Q2,作Q1M⊥y轴于点M,Q2N⊥y轴于点N.先证明△Q1PM≌△PBO,△Q1PM≌△PBO,进而得MQ1=OP=n,MP=OB=3,表示出Q1、Q2的坐标,代入抛物线即可求得N.
解:(1)∵OA=1,OB=OC=3.
∴A(﹣1,0),B(3,0),C(0,3),
∴设y=a(x+1)(x﹣3),
把C(0,3)代入得0=a×1×(﹣3),
解得a=﹣1,
∴y=﹣x2+2x+3;
(2)如图,作DF⊥x轴于点F,交BC于点E,
设直线BC关系式为y=kx+3,
代入B(3,0),
得3k+3=0,
解得k=﹣1,
∴直线BC:y=﹣x+3.
∵点D的横坐标为m,则DF=﹣m2+2m+3,EF=﹣m+3,
∴DE=﹣m2+3m,
∴S=S△ADE+S△BDE=DE OF+DE BF,
=DE OB=(﹣m2+3m)
=﹣(m﹣)2+,
∵﹣<0,
∴S的最大值是;
(3)如图,过点P作PB的垂线,交抛物线于点Q1和Q2,作Q1M⊥y轴于点M,Q2N⊥y轴于点N.
∴∠Q1MP=∠Q2NP=∠BOP=90°,
∵∠Q1PM+∠PQ1M=90°,∠Q1PM+∠BPO=90°,
∴∠PQ1M=∠BPO,
又BP=PQ1,
∴△Q1PM≌△PBO(AAS),
∴MQ1=OP=n,MP=OB=3,
∴Q1(n,n+3),
代入抛物线,得n+3=﹣n2+2n+3,
解得n=1或n=0,
同理,△Q2PN≌△PBO(AAS),
∴Q2(﹣n,n﹣3),
代入抛物线,得n﹣3=﹣n2﹣2n+3,
解得n=或,
综上,存在n 且n=1或n=.
同课章节目录
