2021-2022学年人教版初中数学七年级下册 5.1.1相交线课件 (共18张PPT)
文档属性
| 名称 | 2021-2022学年人教版初中数学七年级下册 5.1.1相交线课件 (共18张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 2.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-12-28 00:00:00 | ||
图片预览




文档简介
(共18张PPT)
人教七年级下册数学
5.1.1 相交线
学习目标:
1.结合具体情境,了解两条直线相交所构成的角,理解邻补角、对顶角的概念和性质。
2.通过观察和动手操作,理解对顶角性质的推导过程,并会用这个性质进行简单的计算,总结解决问题的方法和经验.
3.激情投入,善于发现问题和提出问题,感受学习数学的乐趣.
4.通过辨别对顶角与邻补角,培养识图的能力。
观察
说一说你观察到的现象
合作探究
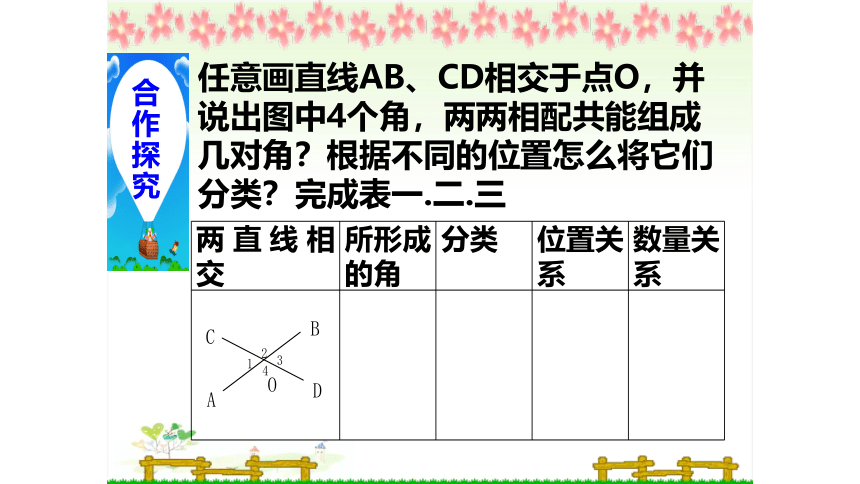
任意画直线AB、CD相交于点O,并说出图中4个角,两两相配共能组成几对角?根据不同的位置怎么将它们分类?完成表一.二.三
两直线相交 所形成的角 分类 位置关系 数量关系
合作探究
两直线相交 所形成的角 分类 位置关系 数量关系
用量角器分别量一量各角的度数,发现各类角的度数有什么关系?把结果填在表四中。
小组交流分享成果
归纳
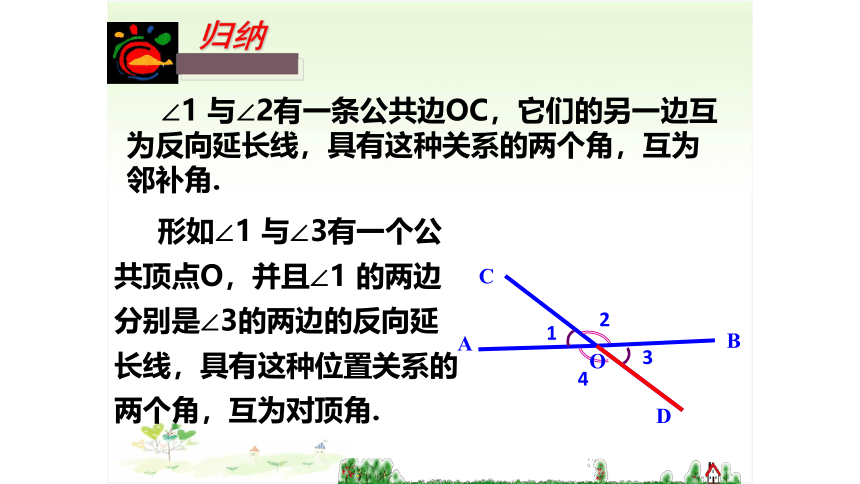
∠1 与∠2有一条公共边OC,它们的另一边互为反向延长线,具有这种关系的两个角,互为邻补角.
形如∠1 与∠3有一个公共顶点O,并且∠1 的两边分别是∠3的两边的反向延长线,具有这种位置关系的两个角,互为对顶角.
1
2
3
4
A
B
C
D
O
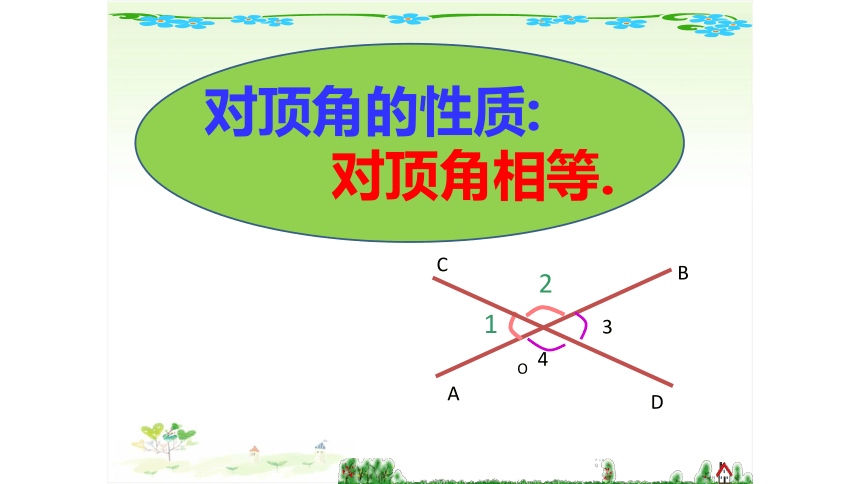
对顶角的性质:
对顶角相等.
1
2
C
A
B
O
3
4
D
1
(1)下列各图中∠1、∠2是对顶角吗?为什么?
2
1
2
1
2
)
(
(
(
)
)
1
(2)下列各图中∠1、∠2是邻补角吗?为什么?
2
1
2
1
2
)
(
(
(
)
(
判断
小试身手
1.如右图所示,∠1和∠2互为________ ,∠1和∠3互为________
2.如图,∠1和∠2是对顶角的图形有________ 个.
3.如下图,两直线相交所成的四个角中,∠1的邻补角是________, ∠1的对顶角是________.
2
∠AOC与∠BOD,∠AOD与∠BOC
∠AOC,∠BOD
变 式 练 习
1.如图,直线AB,CD相交于点O,则:
对顶角有 对,
它们分别是 ,
∠AOD的邻补角是 .
课堂练习
∠7
∠3,∠7
∠6,∠8,∠2,∠4
2.如图,直线l1,l2和l3相交构成8个角,已知∠1=∠5,
∠5是 的对顶角,与∠5相等的角有∠1, ,
与∠5互补的角有 .
3.如图,直线AB与CD相交于点O,ON平分∠DOB,
若∠BOC=110°,则∠AON的度数为 .
145°
B
4.下列说法中正确的个数是( )
①因为∠1与∠2是对顶角,所以∠1=∠2;
②因为∠1与∠2是邻补角,所以∠1=∠2;
③因为∠1与∠2不是对顶角,所以∠1≠∠2;
④因为∠1与∠2不是邻补角,所以∠1+∠2≠180°.
A.0 B.1 C.2 D.3
5.如图,直线AB,CD,EF相交于点O.
(1)写出∠AOC,∠BOE的邻补角;
解:∠AOC的邻补角是∠AOD,∠BOC,∠BOE的邻补角是∠AOE,∠BOF.
(2)写出∠DOA,∠EOC的对顶角;
解:∠DOA的对顶角是∠BOC,∠EOC的对顶角是∠DOF.
(3)如果∠AOC=50°,求∠BOD,∠COB的度数.
解:由对顶角相等,得∠BOD=∠AOC=50°.
由邻补角的定义,得∠COB=180°-∠AOC=180°-50°=130°.
挑战吧
如图,直线a、b相交,∠1+∠3 = 50°,求 ∠2、∠4的度数.
2
)
1
)
(
3
4
(
1
1
)
a
b
(
3
4
(
小组交流分享成果
再试身手
1.完成课本练习。
2.直线AB与CD相交于点O,若 ,求∠BOD的度数
3.直线AB、CD交与点O,且 ∠DOA+∠BOC=220°,
OE平分∠BOD。求∠COE的度数。
A
C
B
D
E
O
颗粒归仓
本 节课你有哪些收获?还有哪些疑问?
再见
人教七年级下册数学
5.1.1 相交线
学习目标:
1.结合具体情境,了解两条直线相交所构成的角,理解邻补角、对顶角的概念和性质。
2.通过观察和动手操作,理解对顶角性质的推导过程,并会用这个性质进行简单的计算,总结解决问题的方法和经验.
3.激情投入,善于发现问题和提出问题,感受学习数学的乐趣.
4.通过辨别对顶角与邻补角,培养识图的能力。
观察
说一说你观察到的现象
合作探究
任意画直线AB、CD相交于点O,并说出图中4个角,两两相配共能组成几对角?根据不同的位置怎么将它们分类?完成表一.二.三
两直线相交 所形成的角 分类 位置关系 数量关系
合作探究
两直线相交 所形成的角 分类 位置关系 数量关系
用量角器分别量一量各角的度数,发现各类角的度数有什么关系?把结果填在表四中。
小组交流分享成果
归纳
∠1 与∠2有一条公共边OC,它们的另一边互为反向延长线,具有这种关系的两个角,互为邻补角.
形如∠1 与∠3有一个公共顶点O,并且∠1 的两边分别是∠3的两边的反向延长线,具有这种位置关系的两个角,互为对顶角.
1
2
3
4
A
B
C
D
O
对顶角的性质:
对顶角相等.
1
2
C
A
B
O
3
4
D
1
(1)下列各图中∠1、∠2是对顶角吗?为什么?
2
1
2
1
2
)
(
(
(
)
)
1
(2)下列各图中∠1、∠2是邻补角吗?为什么?
2
1
2
1
2
)
(
(
(
)
(
判断
小试身手
1.如右图所示,∠1和∠2互为________ ,∠1和∠3互为________
2.如图,∠1和∠2是对顶角的图形有________ 个.
3.如下图,两直线相交所成的四个角中,∠1的邻补角是________, ∠1的对顶角是________.
2
∠AOC与∠BOD,∠AOD与∠BOC
∠AOC,∠BOD
变 式 练 习
1.如图,直线AB,CD相交于点O,则:
对顶角有 对,
它们分别是 ,
∠AOD的邻补角是 .
课堂练习
∠7
∠3,∠7
∠6,∠8,∠2,∠4
2.如图,直线l1,l2和l3相交构成8个角,已知∠1=∠5,
∠5是 的对顶角,与∠5相等的角有∠1, ,
与∠5互补的角有 .
3.如图,直线AB与CD相交于点O,ON平分∠DOB,
若∠BOC=110°,则∠AON的度数为 .
145°
B
4.下列说法中正确的个数是( )
①因为∠1与∠2是对顶角,所以∠1=∠2;
②因为∠1与∠2是邻补角,所以∠1=∠2;
③因为∠1与∠2不是对顶角,所以∠1≠∠2;
④因为∠1与∠2不是邻补角,所以∠1+∠2≠180°.
A.0 B.1 C.2 D.3
5.如图,直线AB,CD,EF相交于点O.
(1)写出∠AOC,∠BOE的邻补角;
解:∠AOC的邻补角是∠AOD,∠BOC,∠BOE的邻补角是∠AOE,∠BOF.
(2)写出∠DOA,∠EOC的对顶角;
解:∠DOA的对顶角是∠BOC,∠EOC的对顶角是∠DOF.
(3)如果∠AOC=50°,求∠BOD,∠COB的度数.
解:由对顶角相等,得∠BOD=∠AOC=50°.
由邻补角的定义,得∠COB=180°-∠AOC=180°-50°=130°.
挑战吧
如图,直线a、b相交,∠1+∠3 = 50°,求 ∠2、∠4的度数.
2
)
1
)
(
3
4
(
1
1
)
a
b
(
3
4
(
小组交流分享成果
再试身手
1.完成课本练习。
2.直线AB与CD相交于点O,若 ,求∠BOD的度数
3.直线AB、CD交与点O,且 ∠DOA+∠BOC=220°,
OE平分∠BOD。求∠COE的度数。
A
C
B
D
E
O
颗粒归仓
本 节课你有哪些收获?还有哪些疑问?
再见
