人教版数学七年级下册9.2 一元一次不等式组的应用 课件(26张ppt)
文档属性
| 名称 | 人教版数学七年级下册9.2 一元一次不等式组的应用 课件(26张ppt) |  | |
| 格式 | ppt | ||
| 文件大小 | 1.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-12-29 07:38:37 | ||
图片预览







文档简介
(共26张PPT)
一元一次不等式组的应用
(1)一个钝角的度数为(5x-30)°,则x的取值范围_______.
填空:
(2)一个长方形足球场的宽是65m,如果它的周长大于330m,面积不大于7150m2,设这个足球场的长为xm,则根据题意列不等式组为_____.
填空:
现有两根木条a和b, a长10cm, b长3cm,如果再找一根木条钉成一个三角形木框,那么对木条c的长度有什么要求
问题1
如果设木条c的长为x cm,那么x仅有小于两边之和还不够,仅有大于两边之差也不行,必须同时满足 x < 10 + 3 和 x > 10 – 3 .
例1.把价格为20元/千克的甲种糖果8千克和价格为18元/千克的乙种糖果若干千克混合,要使总价不超过400元,且糖果不少于15千克,所混合的乙种糖果最少是多少?
解:设所混合的乙种糖果有xkg.根据题意,得
解得
答:乙种糖果最少7千克.
1、有一班学生全住宿,10间宿舍,每间住x人,还有8人没得住,这班学生有 人。
2、幼儿园老师给30个小朋友发糖果,每人发5个,结果有一个小朋友哭了,其他人都有5个,只有他虽然有但不够5个,请问老师拿多少个糖果来发?
答案:146、147、148、149
10x+8
…….
5 5 5 5 5
29人
×5个
怎么我那么少啊?
1个到4个
(30-1)×5例2.一群女生住若干间宿舍,每间住4人,剩19人无房住;每间住6人,有一间宿舍住不满.
(1)设有x间宿舍,请写出x应满足的不等式组
(2)可能有多少间宿舍和多少名学生
思路分析
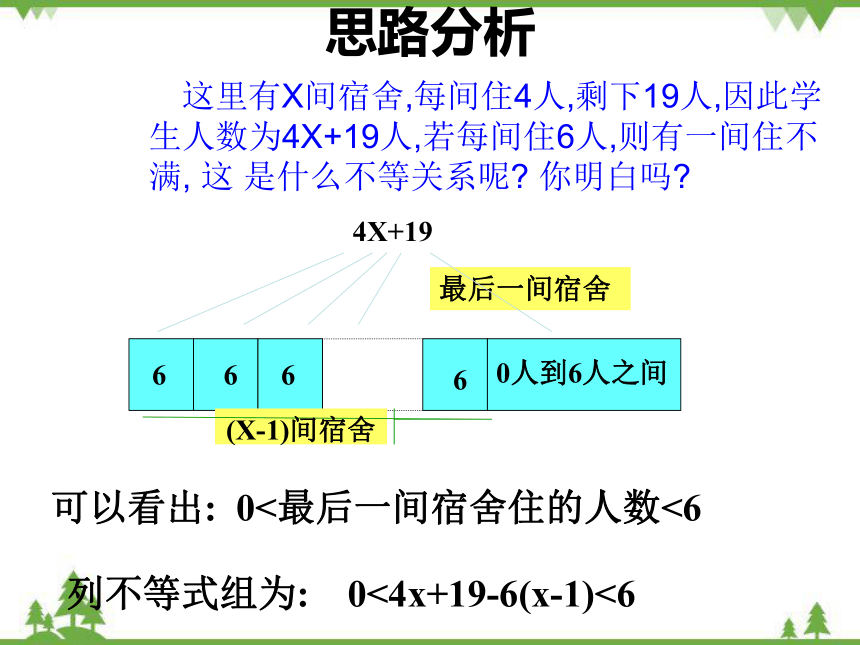
这里有X间宿舍,每间住4人,剩下19人,因此学生人数为4X+19人,若每间住6人,则有一间住不满, 这 是什么不等关系呢 你明白吗
6
6
6
4X+19
0人到6人之间
最后一间宿舍
6
(X-1)间宿舍
列不等式组为: 0<4x+19-6(x-1)<6
可以看出: 0<最后一间宿舍住的人数<6
解: 设有x间宿舍,根据题意得不等式组:
0<4x+19-6(x-1)<6
即: 6x>4x+19
6(x-1)<4x+19
解得: 18.5因为x是整数,所以x=10,11,12.
因此可能有10间宿舍,59名学生或11间宿舍,63名学生或12间宿舍,67名学生.
例3: 某工厂现有甲种原料360kg,乙种原料290kg,计划利用这两种原料生产A,B两种产品共50件,已知生产一件A产品需要甲原料9kg,乙原料3kg,生产一件B产品需要甲原料4kg,乙原料10kg,
(1)设生产X件A种产品,写出X应满足的不等式组。
(2)有哪几种符合的生产方案?
(3)若生产一件A产品可获利700元,生产一件B产品可获利1200元,那么采用哪种生产方案可使生产A、B两种产品的总获利最大?最大利润是多少?
思路分析:
(1)本题的不等关系是:
生产A种产品所需的甲种原料≤360
生产B种产品所需的乙种原料≤290
根据上述关系可列不等式组:
9x+4(50-X)≤360
3x+10(50-x)≤290
解得:30≤X≤32
( 2 ) 可有三种生产方案:A种30件,B种20件或A种31件,B种19件或A种32件,B种18件
1、有堆苹果分给一组小朋友,如果每人5个,还有18个多余,如果每人7个,则还有一位小朋友分不到7个,求苹果的个数和小朋友的人数。
解:设小朋友人数为x人,则苹果数为(5x+18)个,根据题意得:
即:
解得:9x=10、11、12
答:小朋友有10、11或12人,苹果有68、73或78人。
2.某班有若干学生住宿,若每间住4人,则有20人没宿舍住;若每间住8人则有一间没有住满人,试求该班宿舍间数及住宿人数?
分析:第一个条件确定,可设有x间宿舍,则有4x+20个学生。有(x-1)间住了8人,住了8(x-1)人。最后一间为4x+20-8(x-1)人,不确定用不等式.
解:设有x间宿舍,则有4x+20人住宿,依题意可得
4x+20-8(x-1)>0
4x+20-8(x-1)<8
x<7
x>5
解得
因为宿舍是整数所以
x=6; 4x+20=44
答:该班有6间宿舍及44人住宿。
3.小宝和爸爸、妈妈三人在操场上玩跷跷板,爸爸体重为72千克,坐在跷跷板的一端,体重只有妈妈一半的小宝和妈妈一同坐在跷跷板的另一端,这时,爸爸的脚仍然着地。后来,小宝借来一副质量为6千克的哑铃,加在他和妈妈坐的一端,结果小宝和妈妈的脚着地。猜猜小宝的体重约有多少千克?(精确到1千克)
分析:从跷跷板的两种状况可以得到的不等关系
妈妈的体重+小宝的体重 爸爸的体重
妈妈的体重+小宝的体重+6千克 爸爸的体重
<
>
解:设小宝的体重是x千克,则妈妈的体重是2x千克。由题意得
2x+x<72 2x+x+6>72
答案:23
四、讨论交流
4.已知某工厂现有70米,52米的两种布料。现计划用这两种布料生产A、B两种型号的时装共80套,已知做一套A、B型号的时装所需的布料如下表所示,利用现有原料,工厂能否完成任务?若能,有几种生产方案?请你设计出来。
70米 52米
A 0.6米 0.9米
B 1.1米 0.4米
能不能完成啊,我要向厂长交代呀
讨论:1、完成任务是什么意思?
2、70米与52米是否一定要用完?
3、应该设什么为x?
4、用那些关系来列不等式组?
70米 52米
A 0.6米 0.9米
B 1.1米 0.4米
分析:若设生产A型号时装为x套,则生产B型号时装为(80-x)套
X套A型时装需要70米布料 +(80-x)套 B型时装需要的70米布料 70
X套A型时装需要52 米布料+(80-x)套 B型时装需要的52米布料 52
≤
≤
0.6x + 1.1(80-x ) ≤70
0.9x + 0.4(80-x) ≤52
解得:36 x 40
有五种方案:
36套A型和44套B型
37套A型和43套B型
38套A型和42套B型
39套A型和41套B型
40套A型和40套B型
这道题都能做出来,在家等着重点高中的通知书吧。
5.用若干辆载重量为七吨的汽车运一批货物,若每辆汽车只装4吨,则剩下10吨货物,若每辆汽车装满7吨,则最后一辆汽车不满也不空。请问:有多少辆汽车?
分析:设有x辆汽车,则有4x+10吨货物,(x-1)辆汽车装满了7吨,最后一辆装
4x+10-7(x-1)吨,根据不满也不空,可列出不等式
4x+10-7(x-1)>0
4x+10-7(x-1)<7
答案:有4辆汽车或者5辆汽车
6、小宝和爸爸、妈妈三人在操场上玩跷跷板,爸爸体重为72千克,坐在跷跷板的一端;体重只有妈妈一半的小宝和妈妈一同坐在跷跷板的另一端。这时,爸爸的一端仍然着地。后来,小宝借来一副质量为6千克的哑铃加在他和妈妈坐的一端,结果,爸爸被跷起离地。猜猜小宝的体重约是多少?
小宝和爸爸、妈妈三人在操场上玩跷跷板,爸爸体重为72千克,坐在跷跷板的一端;体重只有妈妈一半的小宝和妈妈一同坐在跷跷板的另一端.这时爸爸的一端仍然着地.后来,小宝借来一副质量为6千克的哑铃,加在他和妈妈坐的一端,结果爸爸被跷起离地,猜猜小宝的体重约是多少
在这个问题中,如果设小宝的体重为x千克.
(1)从跷跷板的状况你可以概括出怎样的不等关系
(2)你认为怎样求x的范围,可以尽可能地接近小宝的体重
列不等式:
2x + x < 72
2x + x + 6 > 72
其中x同时满足以上两个不等式
一个量需要同时满足几个不等式的例子,在现实生活中还有很多.
1、把一篮苹果分给几个学生,若每人分4个,则剩余3个;若每人分6个,则最后一个学生最多分得2个,求学生人数和苹果数分别是多少
2、将若干只鸡放在若干个笼里,若每个笼里放4只鸡,则剩下一只鸡无笼可放;若每个笼里放5只鸡,则有一笼无鸡可放.那么至少有几只鸡 多少个笼
作业
1.一堆玩具分给若干个小朋友,若每人分2件,则剩余3件;若前面每人分3件,则最后一个人得到的玩具数不足2件.求小朋友的人数与玩具数
2.已知利民服装厂现有A种布料70米,B种布料52米,现计划用这两种布料生产M,N两种型号的时装共80套,已知做一套M型号时装需A种布料0.6米,B种布料0.9米;做一套N型号时装需A种布料1.1米,B种布料0.4米;若设生产N型号的时装套数为X,用这批布料生产这两种型号的时装有几种方案
火车站有某公司待运的甲种货物1530吨,
乙种货物1150吨,现计划用50节A、B两
种型号的车厢将这批货物运至北京,已知
每节A型货厢的运费是0.5万元,每节B节货
厢的运费是0.8万元;甲种货物35吨和乙种
货物15吨可装满一节A型货厢,甲种货物25
吨和乙种货物35吨可装满一节B型货厢,按
此要求安排A、B两种货厢的节数,共有哪几
种方案 请你设计出来;并说明哪种方案的运
费最少
某自行车厂今年生产销售一种新型自行车,现向你 提供以下信息: ①该厂去年已备用这种自行车车轮10000只,车轮车间今年平均每月可生产车轮1500只,每辆自行车装配2只车轮. ②该厂装搭车间(最后一道工序)每月至少可装搭这种自行车1000,但不超过1200辆. ③该厂已收到各地客户今年订购的这种自行车14500辆的定货单. ④这种自行车出厂销售单价为500元/辆.
该厂今年这种自行车的销售金额为a万元,请你根据上述信息,判断a的取值范围
(1)设:设适当的未知数.
(2)列:列一元一次不等式组.
(3)解:求出一元一次不等式组的解集.
(4)答:写出符合题意的答案.
列一元一次不等式组解应用题的一般步骤:
我来说一说!
一元一次不等式组的应用
(1)一个钝角的度数为(5x-30)°,则x的取值范围_______.
填空:
(2)一个长方形足球场的宽是65m,如果它的周长大于330m,面积不大于7150m2,设这个足球场的长为xm,则根据题意列不等式组为_____.
填空:
现有两根木条a和b, a长10cm, b长3cm,如果再找一根木条钉成一个三角形木框,那么对木条c的长度有什么要求
问题1
如果设木条c的长为x cm,那么x仅有小于两边之和还不够,仅有大于两边之差也不行,必须同时满足 x < 10 + 3 和 x > 10 – 3 .
例1.把价格为20元/千克的甲种糖果8千克和价格为18元/千克的乙种糖果若干千克混合,要使总价不超过400元,且糖果不少于15千克,所混合的乙种糖果最少是多少?
解:设所混合的乙种糖果有xkg.根据题意,得
解得
答:乙种糖果最少7千克.
1、有一班学生全住宿,10间宿舍,每间住x人,还有8人没得住,这班学生有 人。
2、幼儿园老师给30个小朋友发糖果,每人发5个,结果有一个小朋友哭了,其他人都有5个,只有他虽然有但不够5个,请问老师拿多少个糖果来发?
答案:146、147、148、149
10x+8
…….
5 5 5 5 5
29人
×5个
怎么我那么少啊?
1个到4个
(30-1)×5
(1)设有x间宿舍,请写出x应满足的不等式组
(2)可能有多少间宿舍和多少名学生
思路分析
这里有X间宿舍,每间住4人,剩下19人,因此学生人数为4X+19人,若每间住6人,则有一间住不满, 这 是什么不等关系呢 你明白吗
6
6
6
4X+19
0人到6人之间
最后一间宿舍
6
(X-1)间宿舍
列不等式组为: 0<4x+19-6(x-1)<6
可以看出: 0<最后一间宿舍住的人数<6
解: 设有x间宿舍,根据题意得不等式组:
0<4x+19-6(x-1)<6
即: 6x>4x+19
6(x-1)<4x+19
解得: 18.5
因此可能有10间宿舍,59名学生或11间宿舍,63名学生或12间宿舍,67名学生.
例3: 某工厂现有甲种原料360kg,乙种原料290kg,计划利用这两种原料生产A,B两种产品共50件,已知生产一件A产品需要甲原料9kg,乙原料3kg,生产一件B产品需要甲原料4kg,乙原料10kg,
(1)设生产X件A种产品,写出X应满足的不等式组。
(2)有哪几种符合的生产方案?
(3)若生产一件A产品可获利700元,生产一件B产品可获利1200元,那么采用哪种生产方案可使生产A、B两种产品的总获利最大?最大利润是多少?
思路分析:
(1)本题的不等关系是:
生产A种产品所需的甲种原料≤360
生产B种产品所需的乙种原料≤290
根据上述关系可列不等式组:
9x+4(50-X)≤360
3x+10(50-x)≤290
解得:30≤X≤32
( 2 ) 可有三种生产方案:A种30件,B种20件或A种31件,B种19件或A种32件,B种18件
1、有堆苹果分给一组小朋友,如果每人5个,还有18个多余,如果每人7个,则还有一位小朋友分不到7个,求苹果的个数和小朋友的人数。
解:设小朋友人数为x人,则苹果数为(5x+18)个,根据题意得:
即:
解得:9
答:小朋友有10、11或12人,苹果有68、73或78人。
2.某班有若干学生住宿,若每间住4人,则有20人没宿舍住;若每间住8人则有一间没有住满人,试求该班宿舍间数及住宿人数?
分析:第一个条件确定,可设有x间宿舍,则有4x+20个学生。有(x-1)间住了8人,住了8(x-1)人。最后一间为4x+20-8(x-1)人,不确定用不等式.
解:设有x间宿舍,则有4x+20人住宿,依题意可得
4x+20-8(x-1)>0
4x+20-8(x-1)<8
x<7
x>5
解得
因为宿舍是整数所以
x=6; 4x+20=44
答:该班有6间宿舍及44人住宿。
3.小宝和爸爸、妈妈三人在操场上玩跷跷板,爸爸体重为72千克,坐在跷跷板的一端,体重只有妈妈一半的小宝和妈妈一同坐在跷跷板的另一端,这时,爸爸的脚仍然着地。后来,小宝借来一副质量为6千克的哑铃,加在他和妈妈坐的一端,结果小宝和妈妈的脚着地。猜猜小宝的体重约有多少千克?(精确到1千克)
分析:从跷跷板的两种状况可以得到的不等关系
妈妈的体重+小宝的体重 爸爸的体重
妈妈的体重+小宝的体重+6千克 爸爸的体重
<
>
解:设小宝的体重是x千克,则妈妈的体重是2x千克。由题意得
2x+x<72 2x+x+6>72
答案:23
四、讨论交流
4.已知某工厂现有70米,52米的两种布料。现计划用这两种布料生产A、B两种型号的时装共80套,已知做一套A、B型号的时装所需的布料如下表所示,利用现有原料,工厂能否完成任务?若能,有几种生产方案?请你设计出来。
70米 52米
A 0.6米 0.9米
B 1.1米 0.4米
能不能完成啊,我要向厂长交代呀
讨论:1、完成任务是什么意思?
2、70米与52米是否一定要用完?
3、应该设什么为x?
4、用那些关系来列不等式组?
70米 52米
A 0.6米 0.9米
B 1.1米 0.4米
分析:若设生产A型号时装为x套,则生产B型号时装为(80-x)套
X套A型时装需要70米布料 +(80-x)套 B型时装需要的70米布料 70
X套A型时装需要52 米布料+(80-x)套 B型时装需要的52米布料 52
≤
≤
0.6x + 1.1(80-x ) ≤70
0.9x + 0.4(80-x) ≤52
解得:36 x 40
有五种方案:
36套A型和44套B型
37套A型和43套B型
38套A型和42套B型
39套A型和41套B型
40套A型和40套B型
这道题都能做出来,在家等着重点高中的通知书吧。
5.用若干辆载重量为七吨的汽车运一批货物,若每辆汽车只装4吨,则剩下10吨货物,若每辆汽车装满7吨,则最后一辆汽车不满也不空。请问:有多少辆汽车?
分析:设有x辆汽车,则有4x+10吨货物,(x-1)辆汽车装满了7吨,最后一辆装
4x+10-7(x-1)吨,根据不满也不空,可列出不等式
4x+10-7(x-1)>0
4x+10-7(x-1)<7
答案:
6、小宝和爸爸、妈妈三人在操场上玩跷跷板,爸爸体重为72千克,坐在跷跷板的一端;体重只有妈妈一半的小宝和妈妈一同坐在跷跷板的另一端。这时,爸爸的一端仍然着地。后来,小宝借来一副质量为6千克的哑铃加在他和妈妈坐的一端,结果,爸爸被跷起离地。猜猜小宝的体重约是多少?
小宝和爸爸、妈妈三人在操场上玩跷跷板,爸爸体重为72千克,坐在跷跷板的一端;体重只有妈妈一半的小宝和妈妈一同坐在跷跷板的另一端.这时爸爸的一端仍然着地.后来,小宝借来一副质量为6千克的哑铃,加在他和妈妈坐的一端,结果爸爸被跷起离地,猜猜小宝的体重约是多少
在这个问题中,如果设小宝的体重为x千克.
(1)从跷跷板的状况你可以概括出怎样的不等关系
(2)你认为怎样求x的范围,可以尽可能地接近小宝的体重
列不等式:
2x + x < 72
2x + x + 6 > 72
其中x同时满足以上两个不等式
一个量需要同时满足几个不等式的例子,在现实生活中还有很多.
1、把一篮苹果分给几个学生,若每人分4个,则剩余3个;若每人分6个,则最后一个学生最多分得2个,求学生人数和苹果数分别是多少
2、将若干只鸡放在若干个笼里,若每个笼里放4只鸡,则剩下一只鸡无笼可放;若每个笼里放5只鸡,则有一笼无鸡可放.那么至少有几只鸡 多少个笼
作业
1.一堆玩具分给若干个小朋友,若每人分2件,则剩余3件;若前面每人分3件,则最后一个人得到的玩具数不足2件.求小朋友的人数与玩具数
2.已知利民服装厂现有A种布料70米,B种布料52米,现计划用这两种布料生产M,N两种型号的时装共80套,已知做一套M型号时装需A种布料0.6米,B种布料0.9米;做一套N型号时装需A种布料1.1米,B种布料0.4米;若设生产N型号的时装套数为X,用这批布料生产这两种型号的时装有几种方案
火车站有某公司待运的甲种货物1530吨,
乙种货物1150吨,现计划用50节A、B两
种型号的车厢将这批货物运至北京,已知
每节A型货厢的运费是0.5万元,每节B节货
厢的运费是0.8万元;甲种货物35吨和乙种
货物15吨可装满一节A型货厢,甲种货物25
吨和乙种货物35吨可装满一节B型货厢,按
此要求安排A、B两种货厢的节数,共有哪几
种方案 请你设计出来;并说明哪种方案的运
费最少
某自行车厂今年生产销售一种新型自行车,现向你 提供以下信息: ①该厂去年已备用这种自行车车轮10000只,车轮车间今年平均每月可生产车轮1500只,每辆自行车装配2只车轮. ②该厂装搭车间(最后一道工序)每月至少可装搭这种自行车1000,但不超过1200辆. ③该厂已收到各地客户今年订购的这种自行车14500辆的定货单. ④这种自行车出厂销售单价为500元/辆.
该厂今年这种自行车的销售金额为a万元,请你根据上述信息,判断a的取值范围
(1)设:设适当的未知数.
(2)列:列一元一次不等式组.
(3)解:求出一元一次不等式组的解集.
(4)答:写出符合题意的答案.
列一元一次不等式组解应用题的一般步骤:
我来说一说!
