沪科版数学九年级上册 23.2 解直角三角形的方法与技巧 课件(共14张PPT)
文档属性
| 名称 | 沪科版数学九年级上册 23.2 解直角三角形的方法与技巧 课件(共14张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 527.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-12-28 00:00:00 | ||
图片预览





文档简介
(共14张PPT)
解直角三角形
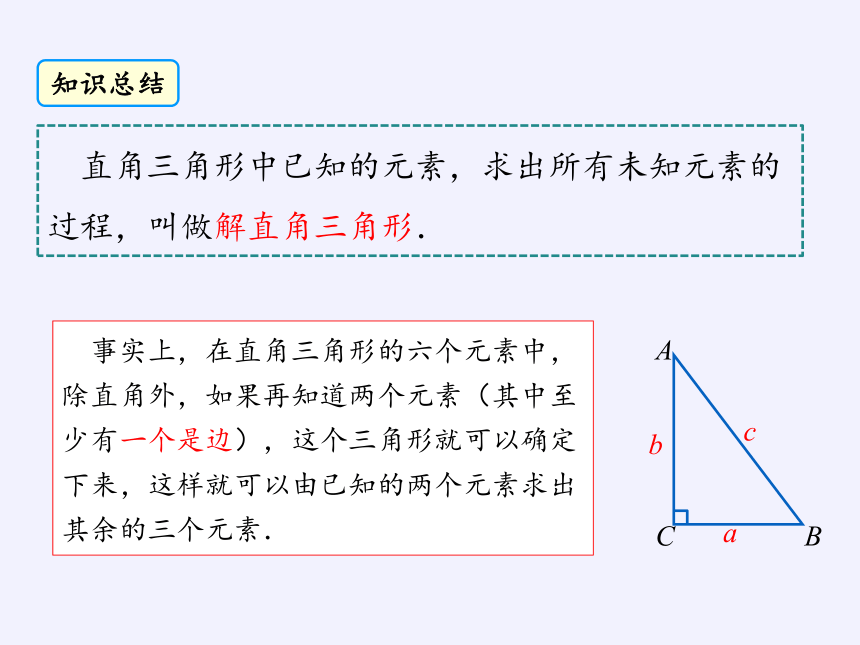
事实上,在直角三角形的六个元素中,除直角外,如果再知道两个元素(其中至少有一个是边),这个三角形就可以确定下来,这样就可以由已知的两个元素求出其余的三个元素.
A
B
a
b
c
C
直角三角形中已知的元素,求出所有未知元素的过程,叫做解直角三角形.
知识总结
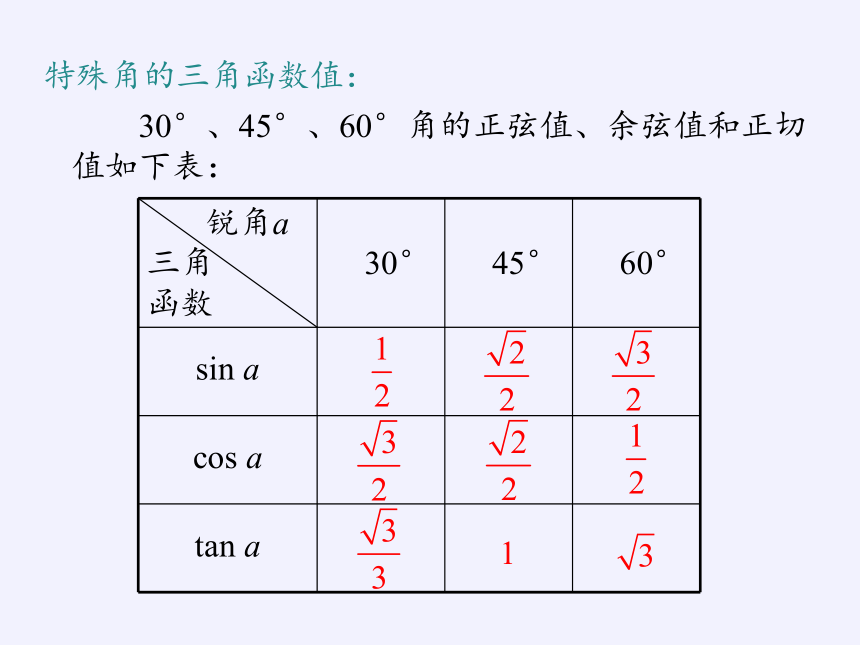
30°、45°、60°角的正弦值、余弦值和正切值如下表:
锐角a 三角 函数 30° 45° 60°
sin a
cos a
tan a
特殊角的三角函数值:
1
锐角三角函数揭示了直角三角形中锐角与边之间的关系,运用锐角三角函数可以解决许多与直角三角形有关的问题,下面就如何运用三角函数解决问题的方法与技巧和大家共同探讨。
课题:解直角三角形的方法与技巧
一、寻找直角三角形
C
A
B
D
1
30°
?
请大家把题目中的已知条件和所求标注在图形中。
分析:首先寻找直角三角形,其次是在直角三角形中求解。本题图中有三个三角形,直角三角形有两个,而根据条件,Rt△ACD可以先直接解,然后为解Rt△ABC提供条件。
二、借助代数方程
D
C
B
A
如图,已知∠C=90°,AB=26,∠CBD=45°,∠DAC=30°,求BC的长。
思考:题型中的有些条件,能直接代入直角三角形中边与边,边与角、角与角之间的公式进行求解吗?(即直接通过公式求解出BC长)
分析:图形中有Rt△DAC和Rt△DBC,但是没有一个直角三角形条件够用,原因是AB=26不属于任何一个直角三角形,可以通过设BC=X,则AC=X+26,让字母参与计算,最后立方程求解。
二、借助代数方程
D
C
B
A
如图,已知∠C=90°,AB=26,∠CBD=45°,∠DAC=30°,求BC的长。
三、构造直角三角形
如图,在四边形中,AD⊥AB,CD⊥BC,∠ADC=120°,BC=14,AD=3,求DC的长。
温馨提示:问题中的图形你根本看不到直角三角形,这时需要你根据条件通过作辅助线构造直角三角形,然后利用直角三角形的相关知识解决问题。
分析:原图中没有直角三角形,但通过延长BA,CD交于点P,从而构造出两个直角三角形Rt △PBC和Rt △PAD,再利用锐角三角函数的相关知识求解。
A
B
C
D
A
B
C
D
P
A
B
C
D
P
如图,在四边形中,AD⊥AB,CD⊥BC,∠ADC=120°,BC=14,AD=3,求DC的长。
四、将实际问题转化为数学问题
解直角三角形的应用可以说涉及到众多的方面,但不管以什么背景出现,将其转化为解直角三角形问题后,归纳起来不外乎以上几种情况而已。
四、将实际问题转化为数学问题
四、将实际问题转化为数学问题
四、将实际问题转化为数学问题
谢 谢
解直角三角形
事实上,在直角三角形的六个元素中,除直角外,如果再知道两个元素(其中至少有一个是边),这个三角形就可以确定下来,这样就可以由已知的两个元素求出其余的三个元素.
A
B
a
b
c
C
直角三角形中已知的元素,求出所有未知元素的过程,叫做解直角三角形.
知识总结
30°、45°、60°角的正弦值、余弦值和正切值如下表:
锐角a 三角 函数 30° 45° 60°
sin a
cos a
tan a
特殊角的三角函数值:
1
锐角三角函数揭示了直角三角形中锐角与边之间的关系,运用锐角三角函数可以解决许多与直角三角形有关的问题,下面就如何运用三角函数解决问题的方法与技巧和大家共同探讨。
课题:解直角三角形的方法与技巧
一、寻找直角三角形
C
A
B
D
1
30°
?
请大家把题目中的已知条件和所求标注在图形中。
分析:首先寻找直角三角形,其次是在直角三角形中求解。本题图中有三个三角形,直角三角形有两个,而根据条件,Rt△ACD可以先直接解,然后为解Rt△ABC提供条件。
二、借助代数方程
D
C
B
A
如图,已知∠C=90°,AB=26,∠CBD=45°,∠DAC=30°,求BC的长。
思考:题型中的有些条件,能直接代入直角三角形中边与边,边与角、角与角之间的公式进行求解吗?(即直接通过公式求解出BC长)
分析:图形中有Rt△DAC和Rt△DBC,但是没有一个直角三角形条件够用,原因是AB=26不属于任何一个直角三角形,可以通过设BC=X,则AC=X+26,让字母参与计算,最后立方程求解。
二、借助代数方程
D
C
B
A
如图,已知∠C=90°,AB=26,∠CBD=45°,∠DAC=30°,求BC的长。
三、构造直角三角形
如图,在四边形中,AD⊥AB,CD⊥BC,∠ADC=120°,BC=14,AD=3,求DC的长。
温馨提示:问题中的图形你根本看不到直角三角形,这时需要你根据条件通过作辅助线构造直角三角形,然后利用直角三角形的相关知识解决问题。
分析:原图中没有直角三角形,但通过延长BA,CD交于点P,从而构造出两个直角三角形Rt △PBC和Rt △PAD,再利用锐角三角函数的相关知识求解。
A
B
C
D
A
B
C
D
P
A
B
C
D
P
如图,在四边形中,AD⊥AB,CD⊥BC,∠ADC=120°,BC=14,AD=3,求DC的长。
四、将实际问题转化为数学问题
解直角三角形的应用可以说涉及到众多的方面,但不管以什么背景出现,将其转化为解直角三角形问题后,归纳起来不外乎以上几种情况而已。
四、将实际问题转化为数学问题
四、将实际问题转化为数学问题
四、将实际问题转化为数学问题
谢 谢
