沪科版数学九年级上册 22.3 相似三角形的性质 课件(共16张PPT)
文档属性
| 名称 | 沪科版数学九年级上册 22.3 相似三角形的性质 课件(共16张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 198.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-12-28 18:06:53 | ||
图片预览

文档简介
(共16张PPT)
22.3 相似三角形的性质
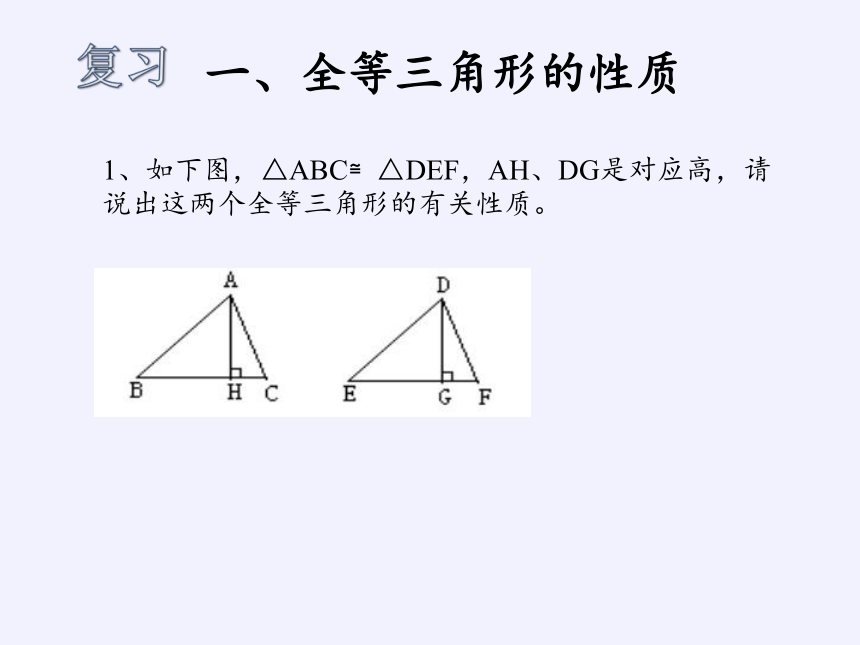
1、如下图,△ABC≌△DEF,AH、DG是对应高,请说出这两个全等三角形的有关性质。
复习
一、全等三角形的性质
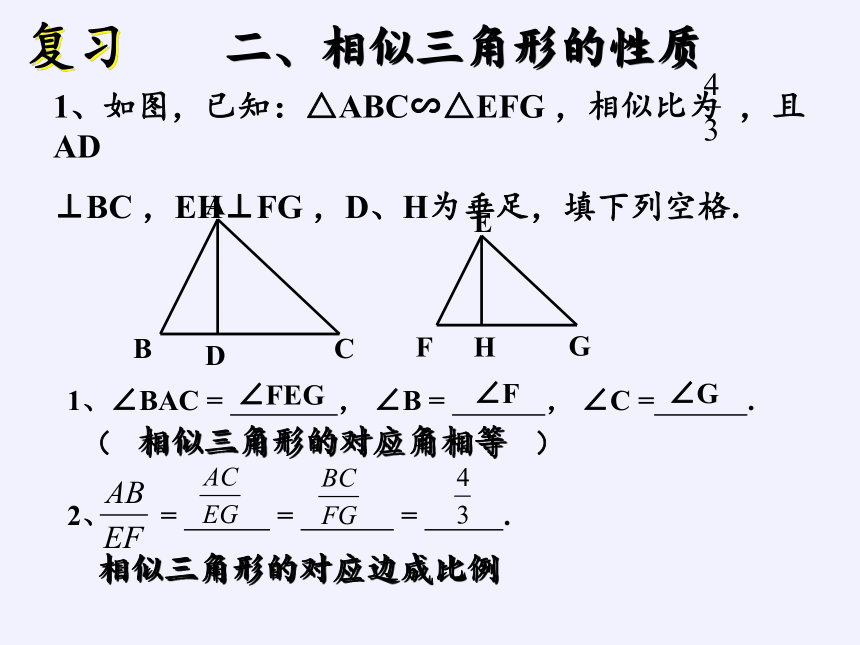
二、相似三角形的性质
复习
1、如图,已知:△ABC∽△EFG ,相似比为 ,且AD
⊥BC ,EH⊥FG ,D、H为垂足,填下列空格.
A
B
C
D
E
F
G
H
1、∠BAC = , ∠B = , ∠C = .
( )
2、 = = = .
∠FEG
∠F
∠G
相似三角形的对应角相等
相似三角形的对应边成比例
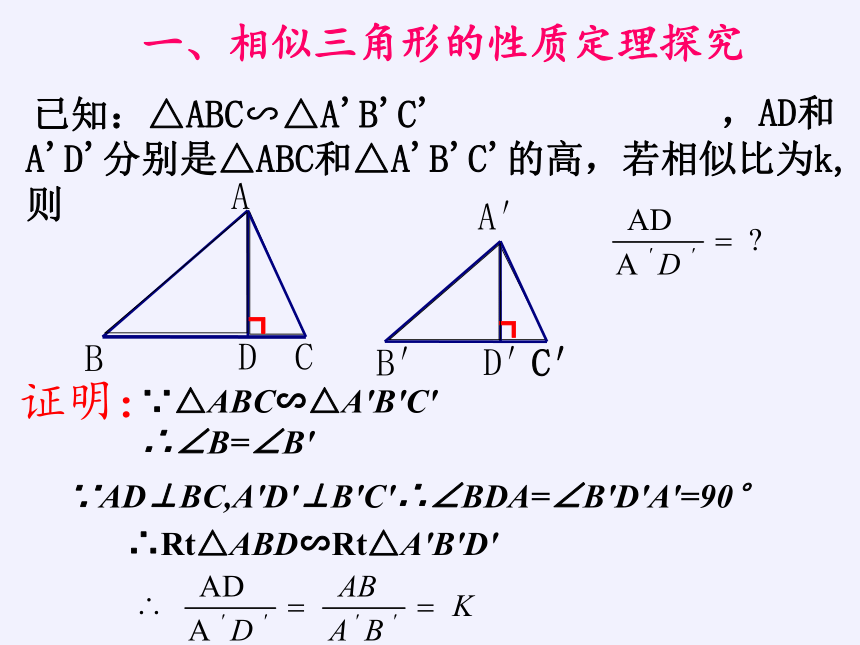
已知:△ABC∽△A'B'C'
,AD和A'D'分别是△ABC和△A'B'C'的高,若相似比为k,则
D′
C′
B′
┓
D
A
B
C
A′
┓
证明:
∵△ABC∽△A′B′C′
∴∠B=∠B′
∵AD⊥BC,A′D′⊥B′C′∴∠BDA=∠B′D′A′=90°
∴Rt△ABD∽Rt△A′B′D′
一、相似三角形的性质定理探究
D′
C′
D
A
B
C
A′
B′
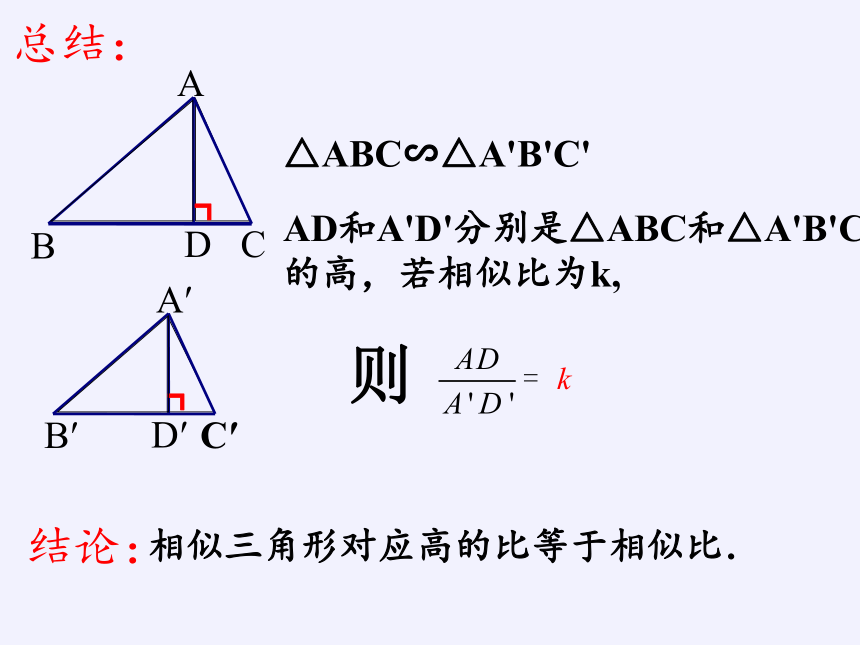
△ABC∽△A'B'C'
AD和A'D'分别是△ABC和△A'B'C'
的高,若相似比为k,
┓
┓
相似三角形对应高的比等于相似比.
结论:
总结:
则
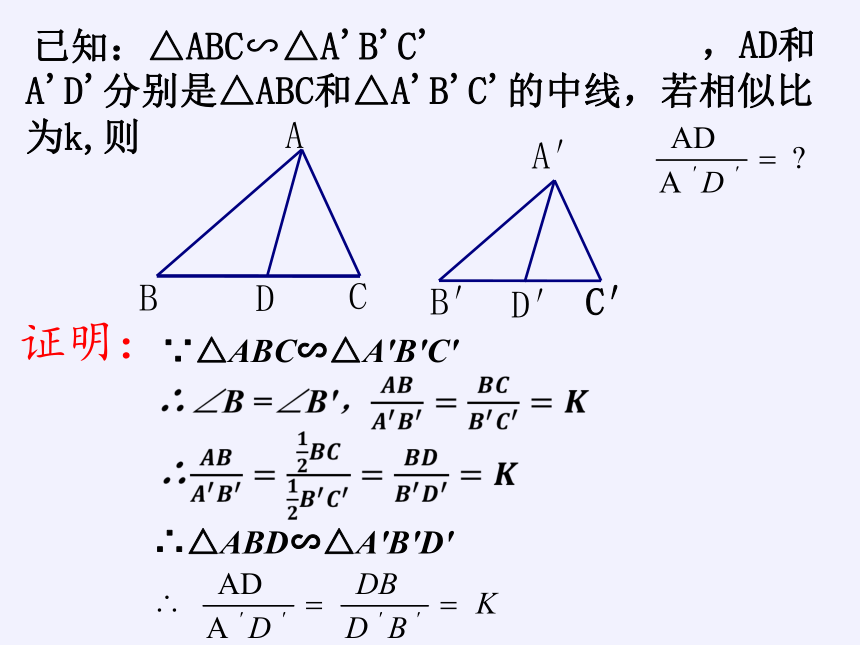
已知:△ABC∽△A'B'C'
,AD和A'D'分别是△ABC和△A'B'C'的中线,若相似比为k,则
D′
C′
B′
D
A
B
C
A′
证明:
∵△ABC∽△A′B′C′
∴△ABD∽△A′B′D′
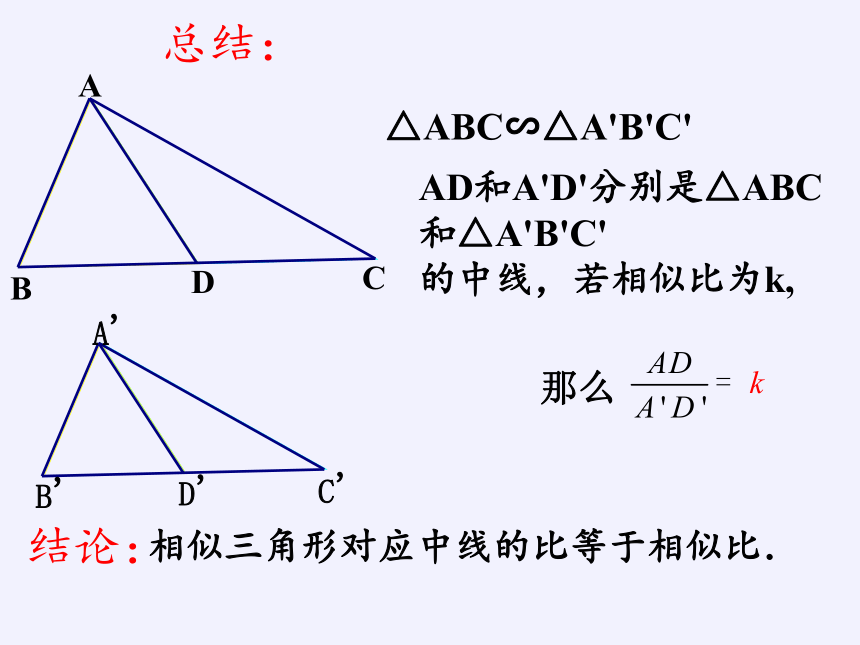
△ABC∽△A'B'C'
AD和A'D'分别是△ABC和△A'B'C'
的中线,若相似比为k,
那么
D
A
B
C
D'
A'
B'
C'
相似三角形对应中线的比等于相似比.
结论:
总结:
已知:△ABC∽△A'B'C'
,AD和A'D'分别是△ABC和△A'B'C'的角平分线,若相似比为k,则
证明:
∵△ABC∽△A′B′C′
∴∠B=∠B′;∠BAC=∠B′A′C′
∵∠BDA= ∠BAC
∴△ABD∽△A′B′D′
D
A
B
C
D'
A'
B'
C'
∵∠B′D′A′= ∠B′A′C′
∴∠BAD=∠B′A′D′
D'
A'
B'
C'
D
A
B
C
相似三角形对应角平分线的比等于相似比.
结论:
△ABC∽△A'B'C'
AD和A'D'分别是△ABC和△A'B'C'的角平分线,若相似比为k,
那么
总结:
相似三角形的性质定理1
小结
1.相似三角形对应高的比等于相似比.
3.相似三角形对应角平分线的比等于相似比.
2.相似三角形对应中线的比等于相似比.
1、 两个相似三角形的相似比为2 : 3,它们的对应角平分线之比为________,对应高比为_______,对应中线的比为_________。
简单应用
例1.如图: △ABC是一块锐角三角形的余料,边长 BC=80cm,高AD=60cm,要把它加工成长方形零件,使长方形的两边之比为2:1,且长方形的一边位于BC上,另外两个顶点在AB、AC上,这个长方形的零件的边长为多少?
R
Q
S
P
A
C
B
D
E
二、相似三角形的性质应用
R
Q
S
P
A
C
B
D
E
解:设加工后的长方形零件 长PQ=2Xcm, 宽PS=Xcm;
∵PQ//BC
∴△APQ∽ △ABC
∴解得:x=24
∴2x=48
答:这个零件的长和宽分别为24cm和48cm.
G
H
F
E
A
C
B
D
1、如图: △ABC是一块锐角三角形的余料,边长 BC=80cm,高AD=60cm,要把它加工成正方形零件,使正方形的一边在BC上,其余两个顶点在AB、AC上,这个正方形的零件的边长为多少?
解:设正方形的边长为x cm.
∵EH∥BC ∴△AEH∽△ABC
N
∴这个正方形的零件的边长为 cm。
三、巩固练习
1.已知:如图:FIHG为矩形,AD⊥BC于D,
,BC=36cm,AD=12cm 。
求:矩形FGNI的周长。
全等三角形与相似三角形性质比较
全等三角形 相似三角形
对应边相等 对应边的比等于相似比
对应角相等 对应角相等
对应高相等 对应高的比等于相似比
对应中线相等 对应中线的比等于相似比
对应角平分线相等 对应角平分线的比等于相似比
归纳总结
谢 谢
22.3 相似三角形的性质
1、如下图,△ABC≌△DEF,AH、DG是对应高,请说出这两个全等三角形的有关性质。
复习
一、全等三角形的性质
二、相似三角形的性质
复习
1、如图,已知:△ABC∽△EFG ,相似比为 ,且AD
⊥BC ,EH⊥FG ,D、H为垂足,填下列空格.
A
B
C
D
E
F
G
H
1、∠BAC = , ∠B = , ∠C = .
( )
2、 = = = .
∠FEG
∠F
∠G
相似三角形的对应角相等
相似三角形的对应边成比例
已知:△ABC∽△A'B'C'
,AD和A'D'分别是△ABC和△A'B'C'的高,若相似比为k,则
D′
C′
B′
┓
D
A
B
C
A′
┓
证明:
∵△ABC∽△A′B′C′
∴∠B=∠B′
∵AD⊥BC,A′D′⊥B′C′∴∠BDA=∠B′D′A′=90°
∴Rt△ABD∽Rt△A′B′D′
一、相似三角形的性质定理探究
D′
C′
D
A
B
C
A′
B′
△ABC∽△A'B'C'
AD和A'D'分别是△ABC和△A'B'C'
的高,若相似比为k,
┓
┓
相似三角形对应高的比等于相似比.
结论:
总结:
则
已知:△ABC∽△A'B'C'
,AD和A'D'分别是△ABC和△A'B'C'的中线,若相似比为k,则
D′
C′
B′
D
A
B
C
A′
证明:
∵△ABC∽△A′B′C′
∴△ABD∽△A′B′D′
△ABC∽△A'B'C'
AD和A'D'分别是△ABC和△A'B'C'
的中线,若相似比为k,
那么
D
A
B
C
D'
A'
B'
C'
相似三角形对应中线的比等于相似比.
结论:
总结:
已知:△ABC∽△A'B'C'
,AD和A'D'分别是△ABC和△A'B'C'的角平分线,若相似比为k,则
证明:
∵△ABC∽△A′B′C′
∴∠B=∠B′;∠BAC=∠B′A′C′
∵∠BDA= ∠BAC
∴△ABD∽△A′B′D′
D
A
B
C
D'
A'
B'
C'
∵∠B′D′A′= ∠B′A′C′
∴∠BAD=∠B′A′D′
D'
A'
B'
C'
D
A
B
C
相似三角形对应角平分线的比等于相似比.
结论:
△ABC∽△A'B'C'
AD和A'D'分别是△ABC和△A'B'C'的角平分线,若相似比为k,
那么
总结:
相似三角形的性质定理1
小结
1.相似三角形对应高的比等于相似比.
3.相似三角形对应角平分线的比等于相似比.
2.相似三角形对应中线的比等于相似比.
1、 两个相似三角形的相似比为2 : 3,它们的对应角平分线之比为________,对应高比为_______,对应中线的比为_________。
简单应用
例1.如图: △ABC是一块锐角三角形的余料,边长 BC=80cm,高AD=60cm,要把它加工成长方形零件,使长方形的两边之比为2:1,且长方形的一边位于BC上,另外两个顶点在AB、AC上,这个长方形的零件的边长为多少?
R
Q
S
P
A
C
B
D
E
二、相似三角形的性质应用
R
Q
S
P
A
C
B
D
E
解:设加工后的长方形零件 长PQ=2Xcm, 宽PS=Xcm;
∵PQ//BC
∴△APQ∽ △ABC
∴解得:x=24
∴2x=48
答:这个零件的长和宽分别为24cm和48cm.
G
H
F
E
A
C
B
D
1、如图: △ABC是一块锐角三角形的余料,边长 BC=80cm,高AD=60cm,要把它加工成正方形零件,使正方形的一边在BC上,其余两个顶点在AB、AC上,这个正方形的零件的边长为多少?
解:设正方形的边长为x cm.
∵EH∥BC ∴△AEH∽△ABC
N
∴这个正方形的零件的边长为 cm。
三、巩固练习
1.已知:如图:FIHG为矩形,AD⊥BC于D,
,BC=36cm,AD=12cm 。
求:矩形FGNI的周长。
全等三角形与相似三角形性质比较
全等三角形 相似三角形
对应边相等 对应边的比等于相似比
对应角相等 对应角相等
对应高相等 对应高的比等于相似比
对应中线相等 对应中线的比等于相似比
对应角平分线相等 对应角平分线的比等于相似比
归纳总结
谢 谢
